后缀数组（SA）+拓展应用

什么是后缀数组？

后缀

后缀就是从字符串的某个位置i到字符串末尾的子串，我们定义以s的第i个字符为第一个元素的后缀为suff(i)

后缀数组

把s的每个后缀按照字典序排序

后缀数组$sa[i]$就表示排名为i的后缀的起始位置的下标

而它的映射数组$rk[i]$就表示起始位置的下标为i的后缀的排名

简单来说，$sa$表示排名为i的是啥，$rk$表示第$i$个的排名是啥

怎么求后缀数组？

先说最暴力的情况，快排$O(n log n)$每个后缀，但是这是字符串，所以比较任意两个后缀的复杂度其实是$O(n)，$这样一来就是接近$O(n^2 log n)$的复杂度，复杂度太高，所以要优化，

所以我们这里有两个优化。

复杂度过高能不能优化呢？

倍增

首先读入字符串之后我们现根据单个字符排序，当然也可以理解为先按照每个后缀的第一个字符排序。对于每个字符，我们按照字典序给一个排名(当然可以并列)，这里称作关键字。

(注：图片来自havana1)

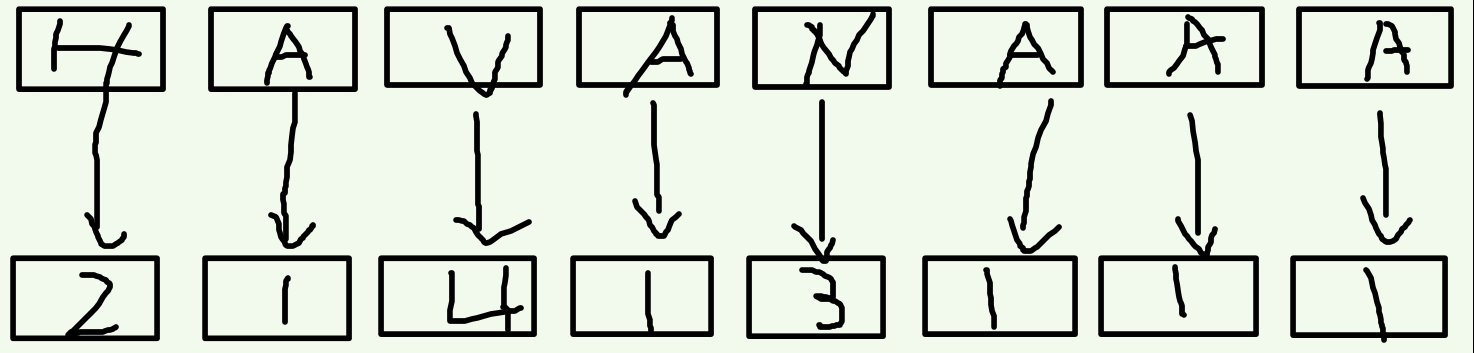
接下来我们再把相邻的两个关键字合并到一起，就相当于根据每一个后缀的前两个字符进行排序。想想看，这样就是以第一个字符(也就是自己本身)的排名为第一关键字，以第二个字符的排名为第二关键字，把组成的新数排完序之后再次标号。没有第二关键字的补零。

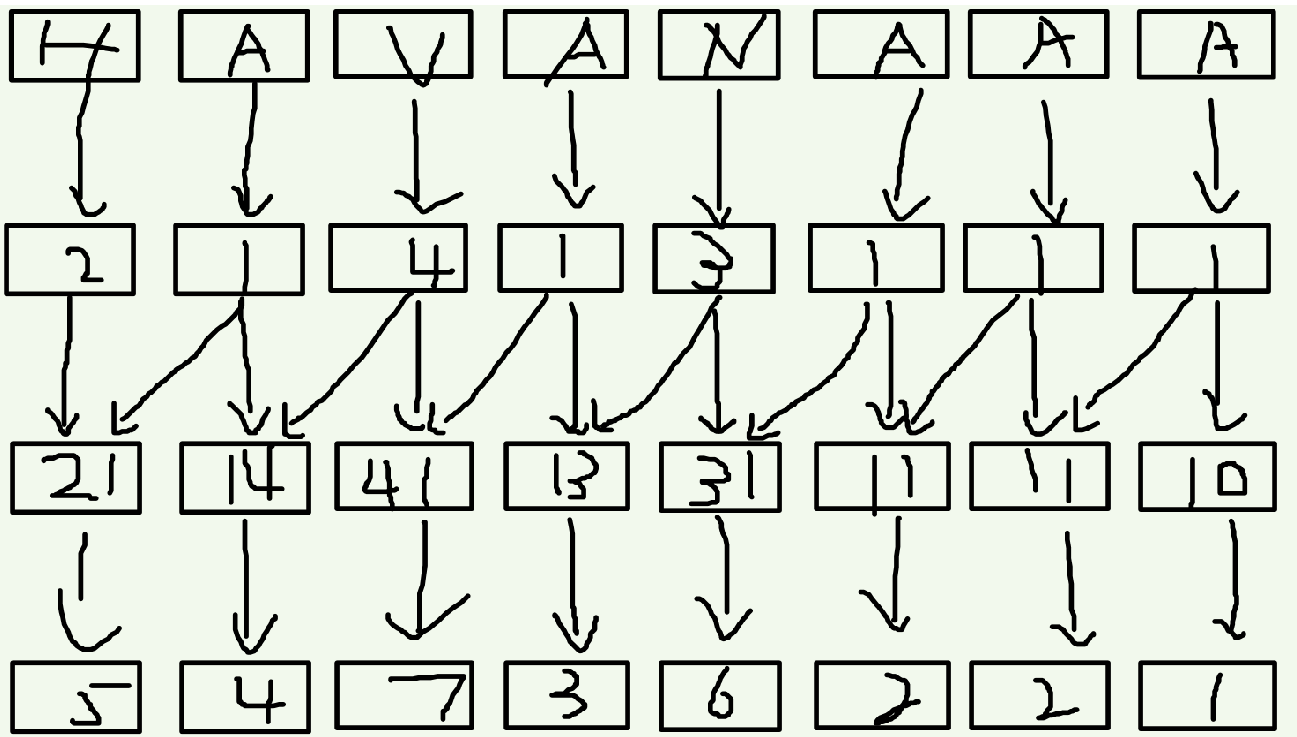
接下来我们对于一个在第i位（第i位指的是下标，是排名会说排名为i）上的关键字，它的第二关键字就是第(i+2)位置上的，联想一下，因为现在第i位上的关键字是suff(i)的前两个字符（i和i+1）的排名，第i+2位置上的关键字是suff(i+2)的前两个字符（i+2和i+3）的排名，这两个一合并，不就是suff(i)的前四个字符的排名吗？方法同上，排序之后重新标号，没有第二关键字的补零。同理我们可以证明，下一次我们要合并的是第i位和第i+4位，以此类推即可…… 这不就是倍增的思想吗？

那么我们什么时候结束呢？很简单，当所有的排名都不同的时候我们直接退出就可以了，因为已经排好了。

显然这样排序的速度稳定在$O(nlog^2 n)$(每次$nlogn$排序，排了$log n$次)

基数排序

如果我们用快排的话，复杂度就是$O(n log^2 n)$ 还是太大。

这里我们用一波基数排序优化一下。在这里我们可以注意到，每一次排序都是排两位数，所以基数排序可以将它优化到$O(n)$级别，总复杂度就是$ O(n log n)$。

介绍一下什么是基数排序，这里就拿两位数举例

我们要建两个桶，一个装个位，一个装十位，我们先把数加到个位桶里面，再加到十位桶里面，这样就能保证对于每个十位桶，桶内的顺序肯定是按个位升序的，很好理解。

具体举个例子基数排序的例子：

73, 22, 93, 43, 55, 14, 28, 65, 39, 81

首先根据个位数的数值，在走访数值时将它们分配至编号0到9的桶子中：

0

1 81

2 22

3 73 93 43

4 14

5 55 65

6

7

8 28

9 39

第二步

接下来将这些桶子中的数值重新串接起来，成为以下的数列：

81, 22, 73, 93, 43, 14, 55, 65, 28, 39

接着再进行一次分配，这次是根据十位数来分配：

0

1 14

2 22 28

3 39

4 43

5 55

6 65

7 73

8 81

9 93

第三步

接下来将这些桶子中的数值重新串接起来，成为以下的数列：

14, 22, 28, 39, 43, 55, 65, 73, 81, 93

这时候整个数列已经排序完毕；如果排序的对象有三位数以上，则持续进行以上的动作直至最高位数为止。

总结

我们现在已经可以$O(nlog n)$来求后缀数组了。

后缀数组的辅助工具-最长公共前缀（LCP）

什么是LCP

我们定义$LCP(i,j)$为$suff(sa[i])$与$suff(sa[j])$的最长公共前缀（请仔细看，是$sa[i]$的后缀，而不是$i$的后缀,这很重要！！！）

LCP的显而易见的性质

显而易见的：

1. $LCP(i,j)=LCP(j,i);$
2. $LCP(i,i)=len(sa[i])=n-sa[i]+1;$

这俩性质有什么用？

对于$i>j$的情况，我们可以把它转化成$i<j$，对于$i=j$的情况，我们可以直接算长度，所以我们直接讨论$i<j$的情况就可以了。

我们怎么求LCP？

每次比较要$O(n)$比较，这太慢了，多次询问复杂度就太高了，肯定要做一些预处理

用于快速求LCP的推论

LCP推论1:$LCP(i,k)=min(LCP(i,j),LCP(j,k))$

推论1：$LCP(i,k)=min(LCP(i,j),LCP(j,k))$ 对于任意$1<=i<=j<=k<=n$

证明：

设$p=min{LCP(i,j),LCP(j,k)}$，则有$LCP(i,j)≥p,LCP(j,k)≥p$。

设$suff(sa[i])=u,suff(sa[j])=v,suff(sa[k])=w$;

所以$u$和$v$的前p个字符相等，$v$和$w$的前$p$个字符相等

所以$u$和$w$的前$p$的字符相等，$LCP(i,k)>=p$

设$LCP(i,k)=q>p$ 那么$q>=p+1$

因为$p=min{LCP(i,j),LCP(j,k)}$，所以$u[p+1]!=v[p+1] $或者$v[p+1]!=w[p+1]$

但是$u[p+1]=w[p+1]$ ，即$u[p+1]!=v[p+1] $且$v[p+1]!=w[p+1]$

这明显是错误的：因为$u[p+1]>=v[p+1]>=w[p+1]$(字符串是升序排列的)，而$u[p+1]=w[p+1]$ 。故：$u[p+1]=v[p+1]=w[p+1]$.这和上面推出的$u[p+1]!=v[p+1] $且$v[p+1]!=w[p+1]$ 相矛盾。

所以$LCP(i,k)<=p$

综上所述$LCP(i,k)=p=min{LCP(i,j),LCP(j,k)}$

LCP推论2:$LCP(i,k)=min(LCP(j,j-1))$

推论2：$LCP(i,k)=min(LCP(j,j-1)) $ 对于任意$1<i+1<=j<=k<=n$

利用推论1

我们可以把$i~k$拆成两部分$i-(i+1)$以及$(i+1)-k$

那么$LCP(i,k)=min(LCP(i,i+1),LCP(i+1,k))$

我们可以把$(i+1)- k$再拆，这样就像一个DP，正确性是显然的。

怎么求LCP？

证明关键推论：$h[i]>=h[i-1]-1;$

我们设$height[i]$为$LCP(i,i-1)$，$1<i<=n$，显然$height[1]=0$;

由推论2可得，$LCP(i,k)=min(height[j])$,$ i+1<=j<=k$

我们要利用这些后缀之间的联系求$height[]$数组：

设$h[i]=height[rk[i]]$，同样的，我们若求出$h$数组，只需$height[i]=h[sa[i]]$即可求出$height$数组;

那么现在来证明最关键的一条定理：$h[i]>=h[i-1]-1;$

证明：设$suffix(k)$是排在$suffix(i-1)$前一名的后缀，它们的最长公共前缀是$h[i-1]$。

那么$suffix(k+1)$将排在$suffix(i)$的前面（这里要求$h[i-1]>1$，如果$h[i-1]≤1$，原式显然成立）并且$suffix(k+1)$和$suffix(i)$的最长公共前缀是$h[i-1]-1$，

所以$suffix(i)$和在它前一名的后缀的最长公共前缀至少是$h[i-1]-1$。

按照$h[1],h[2],……,h[n]$的顺序计算,并利用$h$ 数组的性质，时间复杂度可以降为$O(n)$。

即：

　　　rank[i-1] = q-1　suffix(k): rabaa

　　　rank[i-1] = q　 suffix(i-1): 　 racadabrabaa h[i-1] = 2;

　　　……

　　　rank[k-1] = p-1 suffix(k-1): abaa

　　　rank[i] = p suffix(i): 　 acadabrabaa h[i] = 1 (h[i] >= h[i-1]-1 = 1;)

求h数组

可以令$i$从$1$循环到$n$（此循环中i的意义为$suffix(i)$）按照如下方法依次算出$h[i]$：

（1）若 $Rank[i]=1$，则$h[i]=0$。字符比较次数为$0$。

（2）若$i=1$或者$h[i-1]≤1$，则直接暴力算，将$Suffix(i)$和$Suffix(Rank[i]-1)$从第一个字符开始依次比较直到有字符不相同，由此计算出$h[i]$。因为$h[i-1]<=1$且$h[i-1]<=1$的个数最多也就是$n$个，$i=1$的情况也只有一次，所以这一步复杂度也是不超过$O(n)$的

（3）否则，说明$i>1$，$Rank[i]>1$，$h[i-1]>1$，根据性质2，$Suffix(i)$和$Suffix(Rank[i]-1)$至少有前$h[i-1]-1$ 个字符是相同的，于是字符比较可以从$h[i-1]$开始，直到某个字符不相同，由此计算出$h[i]$。字符比较次数为$h[i]-(h[i-1]-1)+1=h[i]-h[i-1]+2$。

　　可求得最后算法复杂度为$O(n)$。

从h反推出height数组

$h[i]=height[rk[i]]$，可以推出$height[i]=h[sa[i]]$

通过RMQ来做LCP

由推论2可知：$LCP(i,k)=min(LCP(j,j-1))$ ，$1<i+1<=j<= k <=n$

$height[i]$=$LCP(i,i-1)$

故$LCP(i,k)=min(height[ j ])$ ,$1<i+1<=j<= k <=n$

后缀数组+LCP用来解决什么问题？

1.利用LCP的性质将平凡LCP问题转化为height数组上的RMQ问题

solution：比如我们多次查询字符串的第$x$位的后缀和第$y$位的后缀的最长公共前缀的长度：

因为LCP(i,k)里的i和k是指排名,所以我们可以通过先求$i=rank[x],k=rank[y]$

然后查询区间$1<i+1<=j<=k<=n$中$min(height[j])$，这转换成了一个RMQ问题了

然后log查询，效率十分高。

2.有一个字符串s，求它的子串中至少出现过两次的最长的子串。

Solution：考虑$height$的定义：两个rank值相近的字符串的最长公共前缀，那么很显然答案就是
$max(height[i])(i∈(1,n))$

3.有一个字符串s，求它的子串中至少出现过两次的最长的子串（不可重叠）。

Solution：

4.给定一个字符串s，求它不同的子串的个数

Solution：考虑有$height[i ]$的重复，