2020牛客暑期多校训练营（第二场）

Chillstep个人补题记录：

A	B	C	D	E	F	G	H	I	J	K
	√	√	√		√				√	√

Problem A

Problem B

题意：

给n个点(不包括原点)，问经过原点的圆最多可以和多少个点相交？

思路：

枚举两个点，与原点三点确定一个圆。
求得每个点的圆心位置，计算圆心位置设圆方程，然后带入两个点列方程即可，然后解出来带分式的圆心的横纵坐标即可，用分数类维护，维护分数类的时候千万不要gcd约分，直接__int128类型乘就好，gcd约分会超时，这道题应该是有点卡常的。

用数据结构或排序维护每个圆心的出现次数。

code：

//Chillstep ^_^
#include<bits/stdc++.h>
using namespace std;
#define pii pair<int,int>
#define pll pair<ll,ll>
#define pdd pair<double,double>
typedef long long ll;
const int INF=0x3f3f3f3f;
const int MAXN=5e3+2;
const int MOD=998244353;
const double pi=cos(-1);

 
struct frac
{
    ll x,y;
    bool operator<(const frac& b) const
    {
        return __int128(x)*(b.y)<__int128(y)*(b.x);
    }
    bool operator==(const frac& b) const
    {
        return __int128(x)*(b.y)==__int128(y)*(b.x);
    }
 
 
    frac(ll a=0,ll b=0): x(a),y(b) {}
};
 
struct point
{
    frac x,y;
 
    bool operator<(const point& b) const
    {
        return x==b.x?y<b.y:x<b.x;
    }
    bool operator==(const point& b) const
    {
        return x==b.x && y==b.y;
    }
 
    point(ll a=1,ll b=2,ll c=3,ll d=4): x(b*(c*c+d*d)-d*(a*a+b*b),2ll*(b*c-a*d)),y(-a*(c*c+d*d)+c*(a*a+b*b),2ll*(b*c-a*d))
    {
        if(x.y<0) x.x=-x.x,x.y=-x.y;
        if(y.y<0) y.x=-y.x,y.y=-y.y;
    }
};
 
ll a[MAXN],b[MAXN];
int q[4002001];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
 
    for(int i=1;i<=2000;i++)
    {
        q[i*(i-1)/2]=i;
    }
 
    int n;
    cin>>n;
    if(n==0) cout<<"1"<<endl;
    for(int i=1;i<=n;i++) cin>>a[i]>>b[i];
    vector<point>qp;
    for(int i=1;i<=n-1;i++)
    {
        for(int j=i+1;j<=n;j++)
        {
            if(a[i]*b[j]==a[j]*b[i]) continue; //3 points in a line,throw it
            qp.push_back(point(a[i],b[i],a[j],b[j]));
        }
    }
    sort(qp.begin(),qp.end());
    int maxx=0,tep=0;
    for(int i=1;i<(int)qp.size();i++)
    {
        if(qp[i]==qp[i-1])
        {
            tep++;
        }
        else
        {
            maxx=max(maxx,tep);
            tep=1;
        }
    }
    maxx=max(maxx,tep);
    cout<<q[maxx]<<endl;
 
 
    return 0;
}

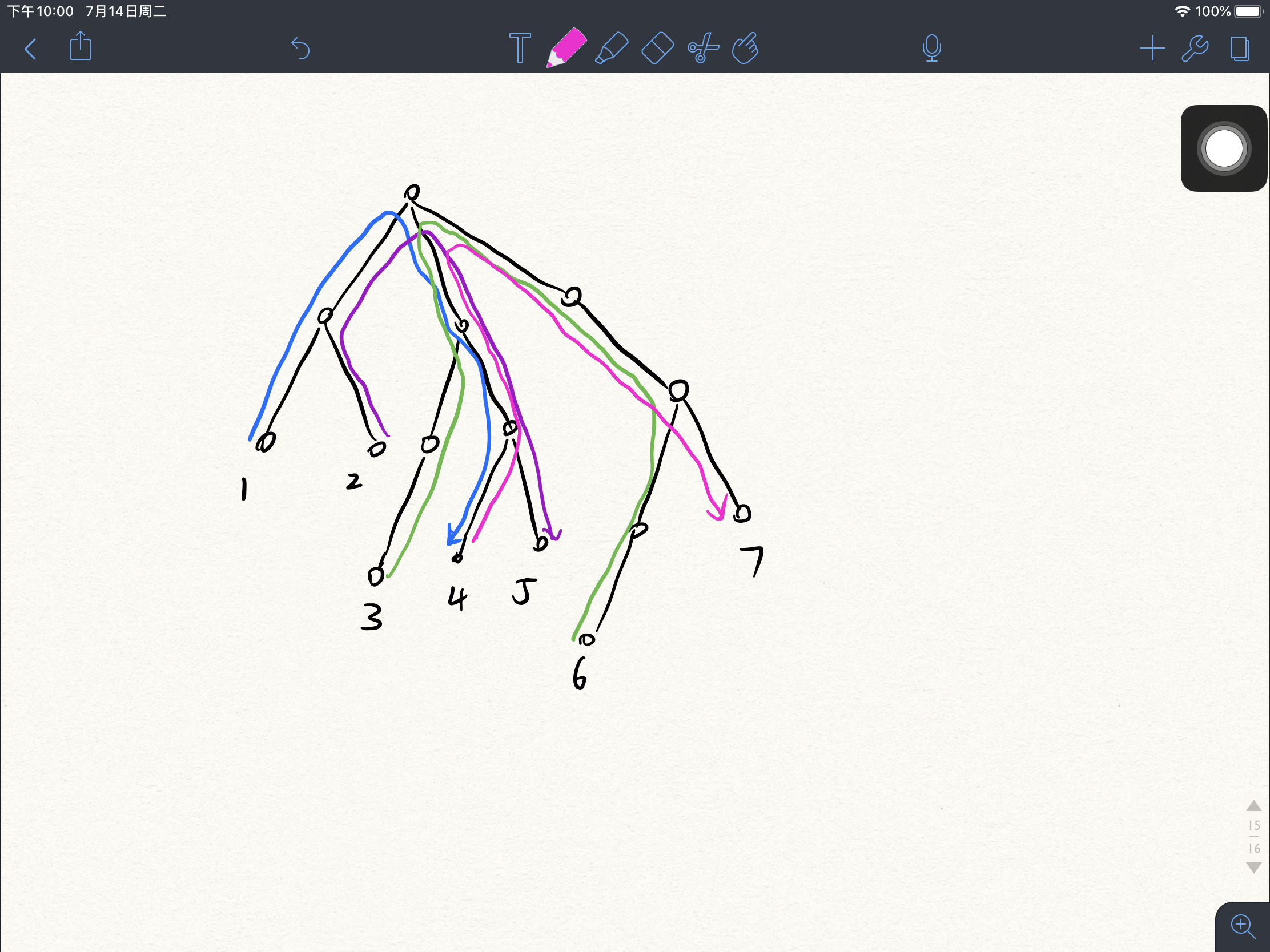
Problem C

题意：

给一棵无向树，然后让你在树中找出一些路径来覆盖这课树的所有边，问最少需要多少条路径。

思路：

画几个图很容易看出来，我们首先为叶子节点表上号(1,2,3,4…x),然后，然后连接1→1+x/2，2→2+x/2，3→3+x/2,….. 以此类推，共需要n/2（上取整）条路径。

举个例子：

code：

#include <iostream>
#include <algorithm>
#include <vector>
 
using namespace std;
 
typedef long long LL;
const int N = 2e5 + 3;
 
vector<int> g[N];
 
vector<int> p;
 
void dfs(int x, int f) {
    if (g[x].size() == 1) p.push_back(x);
    for (auto v : g[x]) {
        if (v == f) {
            continue;
        }
        dfs(v, x);
    }
}
signed main() {
    ios_base::sync_with_stdio(false), cin.tie(0), cout.tie(0);
 
    int n;
    cin >> n;
 
    for (int i = 1; i < n; i++) {
        int a, b;
        cin >> a >> b;
        g[a].push_back(b);
        g[b].push_back(a);
    }
 
    dfs(1, 0);
    int l = p.size();
    cout << (l + 1) / 2 << endl;
    for (int i = 0; i < l / 2; i++) {
        cout << p[i] << ' ' << p[i + l / 2] << endl;
    }
    if (l & 1) {
        cout << p[0] << ' ' << p.back() << endl;
    }
    return 0;
}

Problem D

题意：

给两个时间，求时间差

思路：

换成秒，相减取绝对值即可

code：

//Chillstep ^_^
#include<bits/stdc++.h>
using namespace std;
#define pii pair<int,int>
#define pll pair<ll,ll>
#define pdd pair<double,double>
typedef long long ll;
const int INF=0x3f3f3f3f;
const int MAXN=2e5+2;
const int MOD=998244353;
const double pi=cos(-1);


int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);


    string s1,s2;
    cin>>s1>>s2;
    int a=(s1[6]-'0')*10+s1[7]-'0'+((s1[3]-'0')*10+s1[4]-'0')*60+((s1[0]-'0')*10+s1[1]-'0')*3600;
    int b=(s2[6]-'0')*10+s2[7]-'0'+((s2[3]-'0')*10+s2[4]-'0')*60+((s2[0]-'0')*10+s2[1]-'0')*3600;
    cout<<abs(a-b)<<endl;
    return 0;
}

Problem E

Problem F

题意：

给一个nm矩阵，其中A(i,j)=LCM(i,j)，然后给一个k，求n\m中所有k*k的方块中最大值的和。

思路：

首先要对lcm做一下预处理，可以利用线性筛记忆化的思想来做预处理，这样复杂度就是O(nm)的，再做单调队列二维窗口。

被恶心到了，这题不卡O(nmlog)的做法，非卡一下空间，感觉有点本末倒置了，对着空气debug，我还以为wa了呢，搞半天最多开两个5000*5000的数组，三个数组空间就给卡掉了。没意思没意思。

code:

//Chillstep ^_^
#include<bits/stdc++.h>
using namespace std;
#define pii pair<int,int>
#define pll pair<ll,ll>
#define pdd pair<double,double>
typedef long long ll;
const int INF=0x3f3f3f3f;
const int MAXN=5e3+2;
const int MOD=998244353;
const double pi=cos(-1);

int n,m,k;

int LCM[5002][5002],x[5002][5002];
void init()
{
    for (int i = 1; i <= n; i ++)
        for (int j = 1; j <= m; j ++)
            if (!LCM[i][j])
                for (int k = 1; k * i <= n && k * j <= m; k ++)
                    LCM[k * i][k * j] = k;
    for(int i = 1;i <= n;i++) {
        for(int j = 1;j <= m;j++) {
            LCM[i][j] = i*j/LCM[i][j];
        }
    }


}

int q[MAXN];
int h,t;
void dd_queue(int row)
{
    h=1,t=0;
    for(int i=1; i<=m; i++)
    {
        while(h<=t&&LCM[row][i]>=LCM[row][q[t]]) t--;
        q[++t]=i;
        if(i>=k)
        {
            while(h<=t&&q[h]<i-k+1) h++;
            x[row][i]=LCM[row][q[h]];
        }
    }
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);

    cin>>n>>m>>k;
    init();
    for(int i=1; i<=n; i++) dd_queue(i);
    ll sum=0;
    for(int j=k; j<=m; j++)
    {
        h=1,t=0;
        for(int i=1; i<=n; i++)
        {
            while(h<=t&&x[i][j]>=x[q[t]][j]) t--;
            q[++t]=i;
            if(i>=k)
            {
                while(h<=t&&q[h]<i-k+1) h++;
                sum+=x[q[h]][j];
            }
        }
    }
    cout<<sum<<endl;

    return 0;
}

Problem G

Problem H

Problem I

Problem J

题意：

给一个质数$k$，一个排列$A$，求一个置换$P$，使得{1,2,3,4….}经过k次置换$P$后得到排列A。

思路：

我们考虑一个环若大小为m，置换k次的效果是和置换k mod m一样的。

进行一次置换，相当于把一个数字移动到了下一个位置，建立一个数组$t$,他代表$t[i]$位置的数经过一次置换会转换到$t[i+1]$位置处。

那么对于$A_i=x$，可以理解为一个本来在{1,2,3,4…}排列中第$[x]$个的数，经过置换k次后，最后挪动到了排列A的第i个。我们把这种情况带入，考虑$t[j]=x$ (在x处),则经过一次置换到达的地方的值是$t[j+1]$，经过k次置换后到达的地方的值变成了$t[(j+k)\%m]=i$ (变换到了i处)。也就是说在x处的数k次置换后，会变到i处。

再次观察 $t[(i+k)\%m]=i$，它代表现在i处的数经过k次置换后会到达 $t[(i+k+k)\%m]=g$ 处。

再次观察$t[(i+k+k)\%m]=g$ ，以此类推。

如果冲突就说明不存在这样的置换。

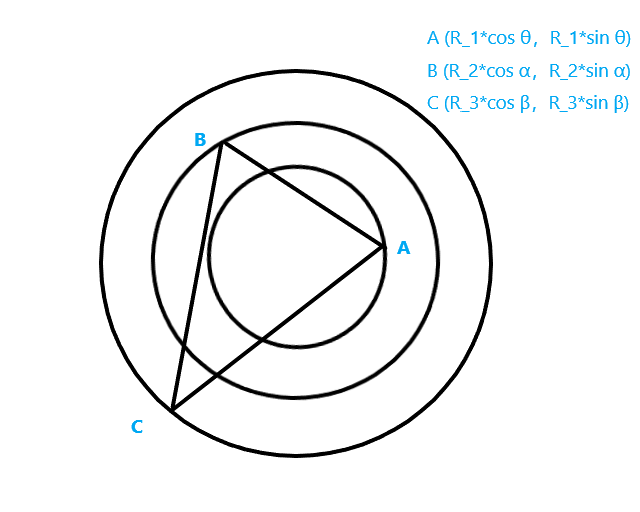
code:

1
2

Problem K

题意：

给出三个同心圆，三个点分别在三个同心圆上，求这三个点组成的三角形的期望面积。

思路：

大概有两个方法.

第一种方法：

第一个方法是标称中里写到的那种，因为有三个点，可以假设一个点不动即可，我们枚举第二个点( 复杂度O(T) )，算第三个点到过第一个点和第二个点直线的距离的期望(可以通过积分来做复杂度$O(\frac{1}{eps})$)，那么最后复杂度是O($\frac{T}{eps}$)

第二种方法：

第二种方法就是场上想到的，可惜感觉精度不太对，没敢写。但是由于题目精度要求比较低，只要求保留最后一位小数，所以是没问题的。

方法就是老老实实的用向量表示出三角形面积。然后对两个角度做积分。

$S=\frac{1}{2} \vec{AB} \vec{AC}=\frac{1}{2} (R_2cosα-R_1 cos θ，R_2sinα-R_1 sin θ) (R_3cosβ-R_1 cos θ，R_3sinβ-R_1 sin θ)$

这里的A点的坐标可以随便选一个点，即A(R_1,0)

$E(S)=\int{0}^{2\pi}\int{0}^{2\pi}|S|dθdα$

记得预处理一下cos sin，不然会超时。

code:

//Chillstep ^_^
#include<bits/stdc++.h>
using namespace std;
#define pii pair<int,int>
#define pll pair<ll,ll>
#define pdd pair<double,double>
typedef long long ll;
const int INF=0x3f3f3f3f;
const int MAXN=5e3+2;
const int MOD=998244353;
const double pi=acos(-1);

/*
double f(double x)
{
    return ; //辛普森积分的函数
}

double simpson(double a, double b)
{
    double c = a + (b - a) / 2;
    return (f(a) + 4 * f(c) + f(b)) * (b - a) / 6;
}

double integral(double L, double R, double Eps)
{
    double mid = L + (R - L) / 2;
    double ST = simpson(L, R), SL = simpson(L, mid), SR = simpson(mid, R);
    if(fabs(SL + SR - ST) <= 15 * Eps)  return SL + SR + (SL + SR - ST) / 15;
    return integral(L, mid, Eps/2) + integral(mid, R, Eps/2);
}
*/


int T=500;
double si[1002],co[1002];
double r[5];


int main()
{
    //ios::sync_with_stdio(false);
    //cin.tie(0);

    double a=0;
    double d=2.0*pi/(double)T;
    for(int i=1;i<=T;i++)
    {
        si[i]=sin(a);
        co[i]=cos(a);
        a+=d;
    }

    int TT;
    cin>>TT;
    while(TT--)
    {
        cin>>r[1]>>r[2]>>r[3];
        sort(r+1,r+4);
        double ans=0;
        for(int i=1;i<=T;i++)
        {
            for(int j=1;j<=T;j++)
            {
                ans+=abs((r[3]*co[j]-r[1])*r[2]*si[i]-(r[2]*co[i]-r[1])*r[3]*si[j]);
            }
        }
        printf("%.1f\n",ans/2.0/(double)T/(double)T);
    }

    return 0;
}

ACM-牛客多校

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议，转载请注明出处！

AHU_SQL_Consise_Tutorial 上一篇

后缀数组(SA)+拓展应用下一篇