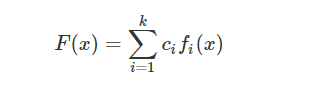What is submodular function(次模函数)
次模函数 submodular function
Introduction
最近在读2003KDD《Maximizing the spread of influence through a social network》这篇文章中遇到了次模函数 submodular function这个东西,整理一下搜集到的东西。
submodular实际上就对“边际效用递减”这个说法的形式化。
submodular function(次模函数)定义
子模态是几何函数的一种性质。一个几何函数$f(x)$的定义要满足下面这个性质。
$f:2^{Ω} → \R$
也就是说:即f(x)的定义域为集合Ω的任何一个子集,值域为实数集。而这个集合函数如果要满足子模态性质的话,还需要满足下面三个等价条件中的任何一个:
(1)对于任何一个$X,Y\subset Ω$且$X\subset Y$,以及对任何一个$x\in Ω$,以下式子成立
$f(X∪x)−f(X)≥f(Y∪x)−f(Y)$
这个就是次模函数的本身定义。
(2)对于任何一个$X,Y\subset Ω$,以下式子成立:
$f(X)+f(Y)≥f(X∪Y)+f(X∩Y)$
证明:
$f(X)-f(X∩Y)≥f(Y∪X)-f(Y)$
$f((X∩Y)∪X)-f(X∩Y)≥f(Y∪X)-f(Y)$
且$(X∩Y)\subset Y$
故等价于(1)定义
(3)对于任何一个$X⊂Ω$及$x1,x2∈Ω$下面的式子一定成立
$f(X∪x1)+f(X∪x2)≥f(X∪x_1,x_2)+f(X)$
证明:
$f(X∪x_1)-f(X)≥f(X∪x_2∪x_1)-f(X∪x_2)$
$(X∪x1)\subset (X∪x_2∪x_1)$
故等价于(1)
推论:
设$f1(x),f2(x),⋯,fk(x)$都是有子模态性质的函数,$c1,c2,⋯,ck $是非负实数,则下面这个函数:
仍然是次模函数。即多个次模函数的非负线性组合仍然是次模函数。
次模函数与贪心方法
次模函数的性质我们称之为子模态,这个子模态的性质主要的作用就是保证我们在贪心求解问题时所得到的近似解不会太差,提供了一个近似保证。即贪心的解$f(x)$的值不会小于$(1-\frac{1}{e})*OPT$,其中$OPT$为最优解。
我们的贪心规则是,每一次将一个新的元素加入到所想要构建的目标集合$x$,迭代k步。我们用$X_i$来表示迭代$i$次之后的$x$集合,初始时$x=\varnothing$。故可以用以下式子表示贪心规则:
现在我们要证明:$\begin{equation}f(x)\geq (1-\frac{1}{e})*OPT\end{equation}$
首先引入一个引理:$\begin{equation} f(A\cup B)-f(A)\leq \sum_{j=1}^{k}{[f(A\cup {b_j})-f(A)]}\end{equation}$
其中$B={b1,b_2,b_3…,b_k}$,此时我们定义$B_i={b_1,b_2,b_3…,b_i}$ ,则:$\begin{equation}\begin{split}f(A\cup B)-f(A)&=\sum{i=1}^{k}{[f(A\cup Bi)-f(A\cup B{i-1})]}\&=\sum{i=1}^{k}{[f(A\cup B{i-1}\cup {bi})-f(A\cup B{i-1})]}\&\leq\sum_{j=1}^{k}{[f(A\cup {b_j})-f(A)]}\end{split}\end{equation}$
设最优解为$T={t1,\cdots,t_k}$, $\delta_i=f(X_i)-f(X{i-1})$,由引理中的不等式可以推出:
$\begin{equation}\begin{split}f(T)&\leq f(Xi\cup T)\&=f(X_i\cup T)-f(X_i)+f(X_i)\&\leq\sum{j=1}^{k}{[f(Xi\cup {t_j})-f(X_i)]}+f(X_i)\&\leq\sum{j=1}^{k}{[\delta{i+1}]}+f(X_i)\&=f(X_i)+k\delta{i+1}\end{split}\end{equation}$
即可得:$\begin{equation}\delta_{i+1}\geq \frac{1}{k}[f(T)-f(X_i)]\end{equation}$
所以:
$\begin{equation}\begin{split}f(X{i+1})&=f(X_i)+\delta{i+1}\&\geq f(X_i)+\frac{1}{k}[f(T)-f(X_i)]\&=(1-\frac{1}{k})f(X_i)+\frac{1}{k}f(T)\end{split}\end{equation}$
故递推式为:$\begin{equation}f(X_i)\geq [1-{(1-\frac{1}{k})}^i]f(T)\end{equation}$
数列求和即可证明:$\begin{equation}f(X_k)\geq [1-{(1-\frac{1}{k})}^k]f(T)\geq [1-\frac{1}{e}]f(T)\end{equation}$
Application:次模函数在影响力最大化问题上的应用
主要在影响力最大化问题中用于证明:贪心法在此问题中是可行的。
$f(X)$,就是初始集合$X$该过程$S$下所返回的集合$P$的大小的平均值。
影响最大化问题就是在固定集合$X$大小$k$的情况下,最大化$f(X)$。我们可以证明这个优化问题是NP-Hard 的。该问题的简化形式为$p{vw}$ 都是1,此时该问题不再是一个随机过程。每个初始点$v$的可达集是固定的,我们可以表示为$Rv$ 。因此,原问题等价于在集合$R_1,⋯,R{|v|} $中找到$k$个集合,使得
$arg\maxu{f(S{i-1}\cup{u})}$
但是,如何证明这个贪心是有效的一个难题,因为这是一个随机过程,每个点的增益在每一个时刻都是一个不同的随机变量,函数表达式也不是一个解析式。
我们现在先从简化问题出发,然后再去求解原问题。而简化问题就是我们之前提到的集合覆盖问题$f(S)$,这个问题其实是子模态的。在$t$时刻节点$v$引发$w$的概率为$p_{vw}$ ,这是一个01分布。事实上这个结果是0还是1与时刻t是无关的,所以我们可以预先生成好这个随机变量。对所有的边进行提前生成随机变量之后,我们就得到了一个图N.
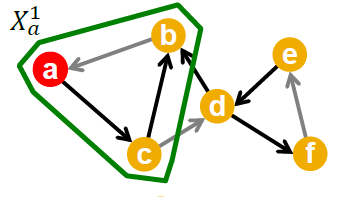
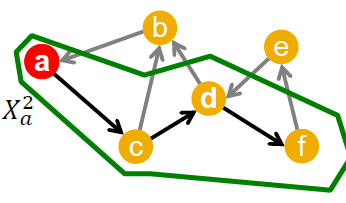
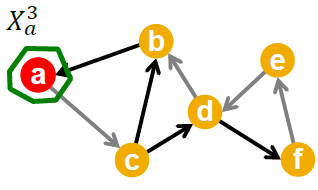
而当$v$引发$w$时,$p_{vw}=1$,否则就等于0.在$N$中的影响最大等价于之前讨论的集合覆盖问题。设生成图$Ni$ 的概率为$pi$ ,设$f_i(X)$为在图$N_i$ 上寻找影响最大的解,则
可以看出这是多个子模态函数的非负线性组合,因此$f(X)$是子模态的。又根据我们在之前证明贪心法在子模态函数上是可行的,所以贪心法对影响最大问题是可行的。
Reference
1.怎么理解次模函数 submodular function? - 彭鹏的回答 - 知乎
https://www.zhihu.com/question/34720027/answer/79260358
2.Submodual http://spiritsaway.info/submodual.html
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!