CH2：Learning to Answer Yes/No

Perceptron Hypothesis Set

$x$为 顾客的特征向量， $y$为是否发卡。

$y$取值为${+1,-1}$。 最后我们得到一个假说Hypothesis $h(x)$, $sign$函数是一个符号函数，在<0,>0，=0分别取-1，1，0。$threshold$为是否发卡的阈值。

我们为了书写简单，把$threshold$收入$w_ix_i$，下标改为从0开始。

那么怎么直观的理解h(x)究竟是什么东西呢？

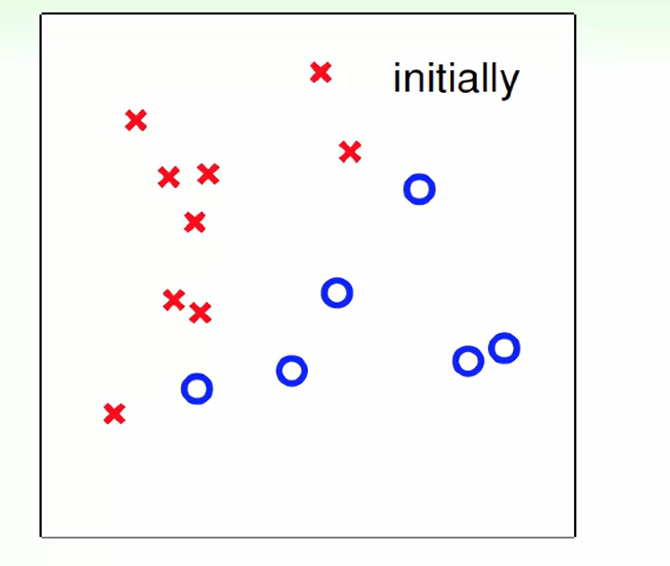
我们把x看作一个只有两维的向量，那么它可以代表平面上的一个点，此时还有一个$w_1,w_2$来影响x向量，每个点 有一个label即圆圈还是叉叉。那么h就代表平面上的一条线。

hypothesis可以看作一堆直线，我们选出一个可以很好划分不同label的直线作为最后的划分函数h(x)即可。h(x)感知机实际上就是一个线性的分类器，即回答yes or no。

Perceptron Learning Algorithm (PLA)

H是一个无限大的集合，因此我们的想法是找一个不是那么优秀的直线，然后对直线进行旋转移动等方法对他进行修正。

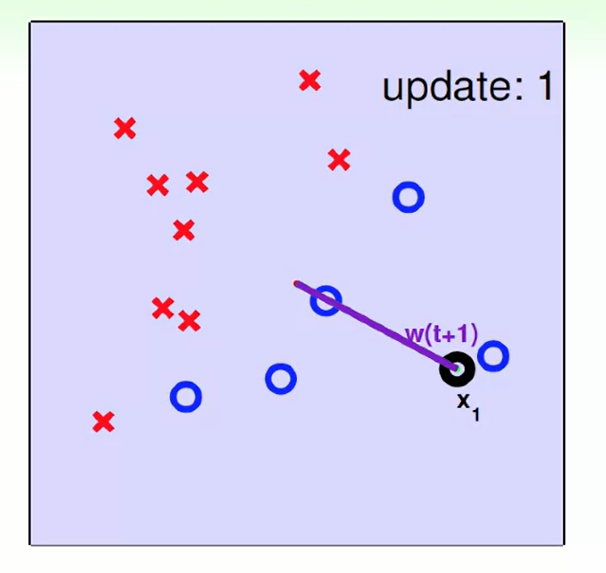
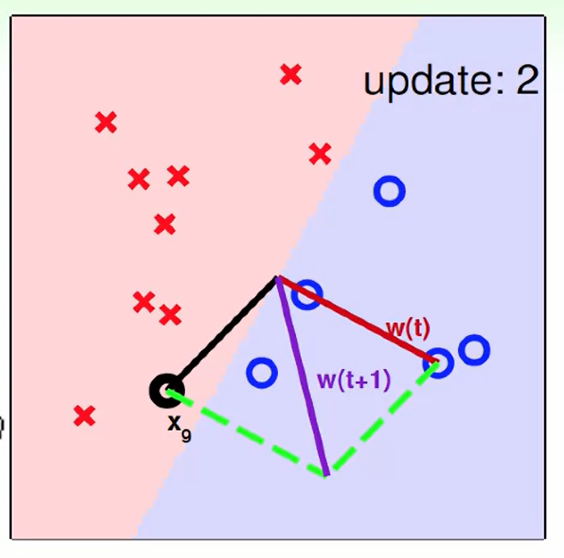
我们找到一个错误的$wt^T$ 使得 $sign(w_t^Tx{n(t)})$被错误的分类(其中n(t)代表第n个样本在第t轮)。因此我们想要对他改进纠错，当$y=+1$时，代表我们想要正的却识别出了负的，因此我们要进行改错，我们把$wt^Tx{n(t)}$可以看作向量$w$和向量$x$的夹角，夹角太大就要减小，即$w$更新为$w+yx$。当$y=-1$时同理。

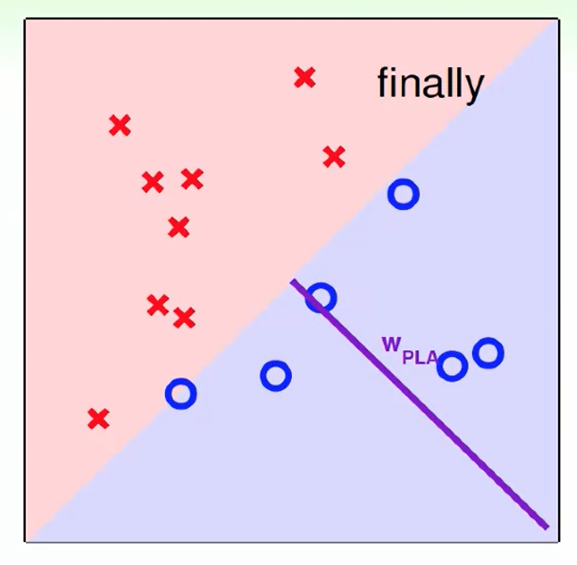
不断改错直到没有错误或者错误最少。

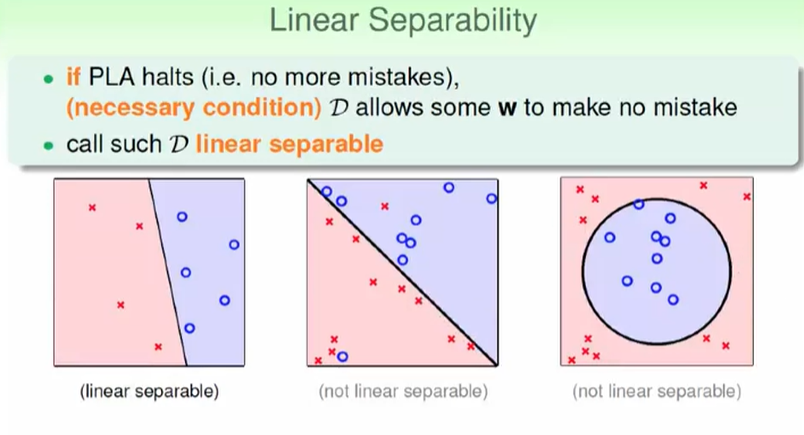
一定会找到全部符合的h吗？ 即使找出来g一定就是h吗？

Guarantee of PLA

后面两种并不能找出一条直线完美切分。

迭代保证的证明：

这里有意思的证明方法是，他对 $w_f$和$w_t$进行了内积，这里采用的度量方式是内积越大，说明和perfect直线越接近。

但是我们仔细想想会发现，内积不仅取决于角度（角度变小可以使得内积变大），同时向量的模也有作用，在你不断迭代，可能由于$w_t$长度影响了内积的大小。

那怎么证明这个问题呢？

但是仔细思考一下 我们是只在错误的时候才做更新，如上图黄色部分。

因此我们再次考虑长度变化问题，看到蓝色的一项是小于0的，因此我们加上不等式关系后我们可以看作0

我们再观察红色项，这个是用来调节的向量，因此无论左右怎么调节，我们直接选一个极值 也就是 $yx$的最大偏移。取完以后我们是可以把$y_n$忽略掉的，因为$y_n$是{-1，+1}是不会影响长度这个标量的。

最后我们可以推到得出下式：

这个式子的常数constant是多少呢？我们做以下推导：

最后这个有关于T的不等式 可以用来估计 调整次数

Non-Separable Data

PLA可以拓展到n维。

PLA的一些问题：我们假设这是线性可分的，我们不知道到底需要多少次迭代，因为$w_f$我们是不知道的，同时真正的样本会存在一些噪音杂质。

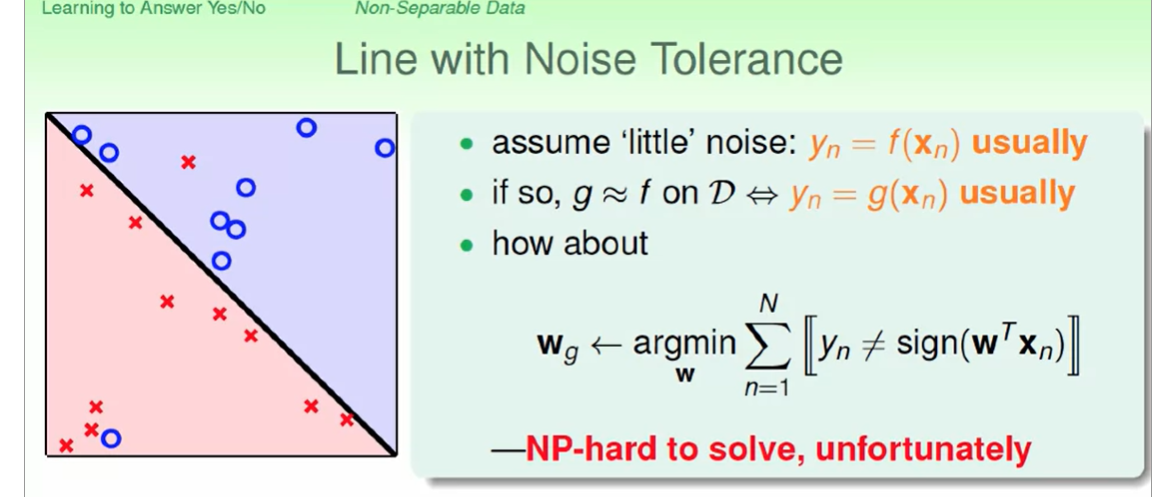
对于下列这样一个问题，我们想找到一个w来线性分割使得 犯的错误最少，但这个是一个NP-hard问题。

虽然我们找到完美的一条线是np-hard问题，但是在一个优秀的复杂度内找到近似最优的一条线还是有解决方法的，如下：Pocket Algorithm

这其实就是一个简单的贪心算法，迭代时我们多考虑一下这条线是否比现在的更优。

答案：A

pocket算法可能和 PLA得到的结果是一样的，因此34都不对，pocket是一定比PLA慢的，因为Pocket需要对比迭代的直线是不是比当前更好，因此要对比所有的数据才可以知道，这会大大浪费时间。