CH4:Feasibility of Learning（学习可行性）

Learning is impossible？

对于有些问题，机器学习给出的答案可能并不是对的，因为样本自身可能符合多个hypothesis，对于不同的hypothesis有不同的结果，这使得结果具有不确定性。

Probability to the Rescue

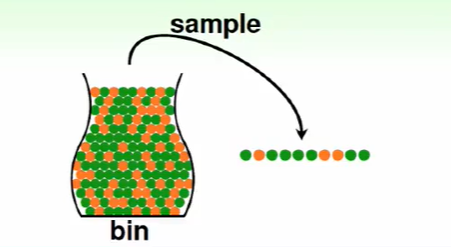
我们估测一个大瓶子里的橘色圆球占比可以通过随机抓一把求橘色圆球占比来估计

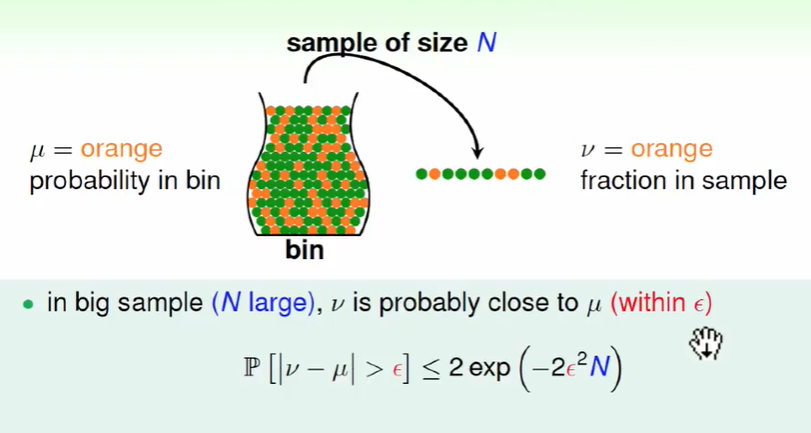
这个依据称为$ Hoeffding$ 霍夫丁不等式。从不等式可以看出当数量N越大，这个准确率是越准确的。

Connection to Learning

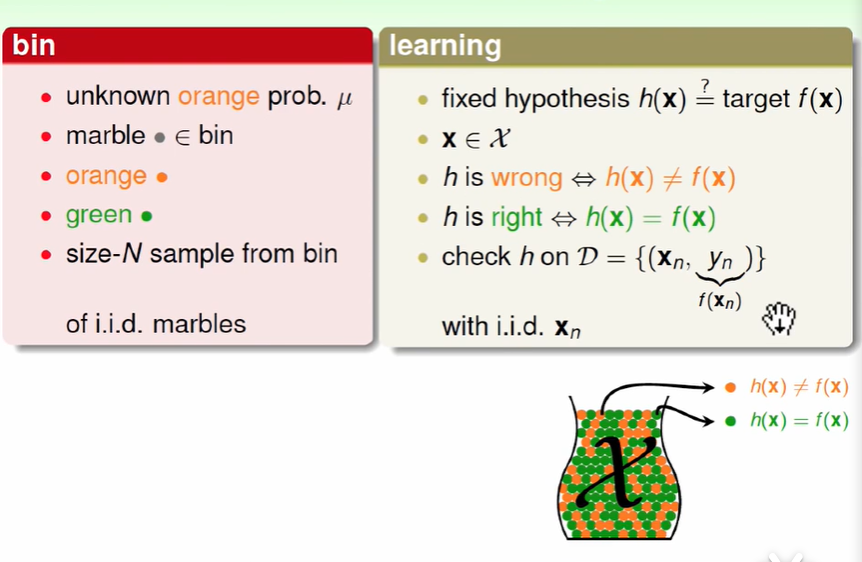
​ 将其转换为机器学习的问题:

• 机器学习中$hypothesis$与目标函数相等的可能性类比于罐子中橙色弹珠的概率问题

• 将罐子中的一颗颗弹珠类比于机器学习中的样本空间x，橙色弹珠类比于$h(x)$和$f(x)$结果不相同，绿色弹珠类比于$h(x)$和$f(x)$结果相同

• 从罐子中抽取的N个弹珠类比于机器学习中的训练样本D，且这两种抽样的样本与总体样本之间是独立同分布的，假设样本的数量N够大且是独立同分布的，可以通过样本中hx和fx不一样的几率大概推断出样本外的样本数据中hx和fx不一样的几率。

---

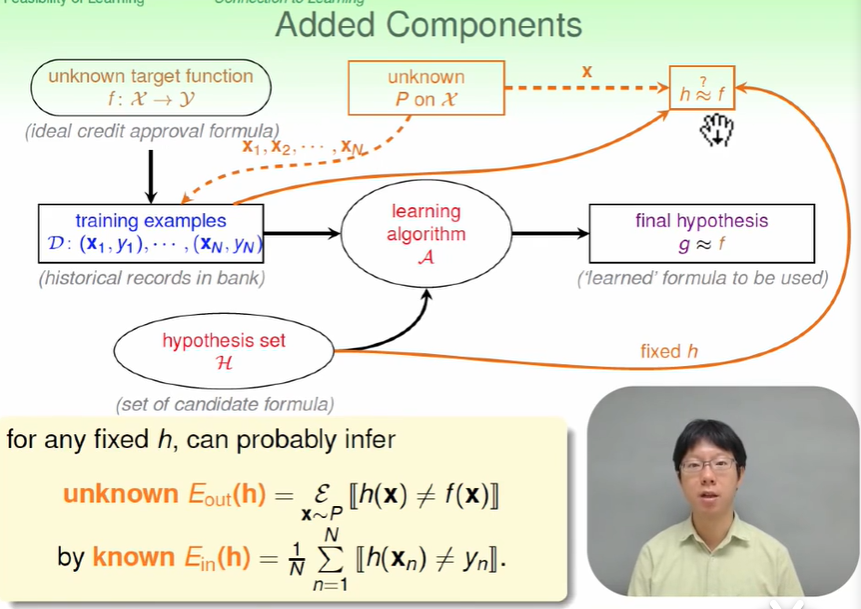
因此机器学习可以类比为，$E{in}(h)$代表着真正的目标函数$f$, 而我们自己提出来的hypothesis在一部分样本上运行效果不错的hypothesis $g$代表着$E{in}(h)$，机器学习就是一个这样的概率问题，在罐子中用一部分球就可以大致的求出概率，机器学习中用一些样本就可以学得和target function差不多的预测函数g。

$E{in}$代表着人手上样本的错误率，$E{out}代表所有的数据的错误率$

类比可知，我们在一个比较大的样本所做到的算法效果很好，那么在所有数据上也会比较好。

---

那么按照上面的说法，我们一定可以找到机器学习比较好的学习效果了，这是和之前所说的Learning is impossible？中的的说法不太一样。我们仔细回想可以发现，这个g并没有人告诉我们，我们要从hypothesis中一大堆的g中选出这个g后，才可以进行我们之前所提到的工作。也就是说你不一定可以找一个在样本上表现很好的（即$E_{in}$ 比较小）的算法。

因此这个并不是学习，而是Verification验证表现，也就是说确认表现好不好（如果在样本表现好，那么很大可能在所有数据上表现很好）。

Connection to Real Learning

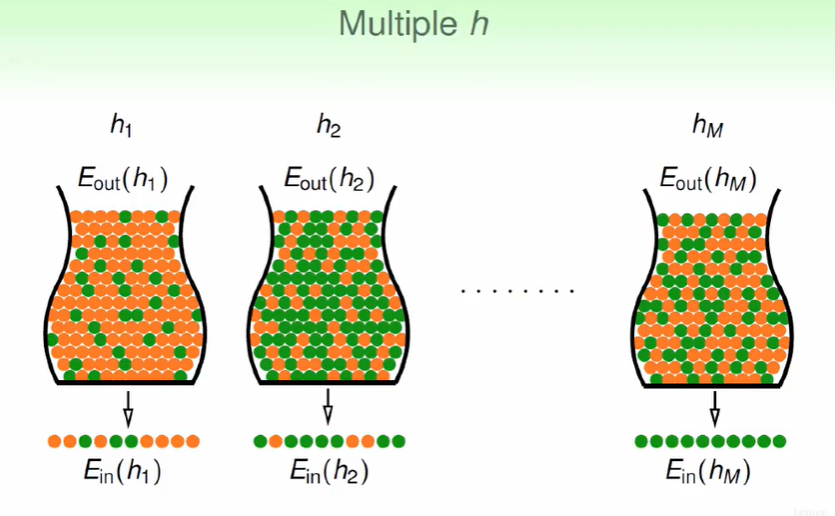
我们的hypothesis中有许多h，那么我们从每个选择十个球来测量绿球的占比，那么这样得出的结果可能不一定是正确的。

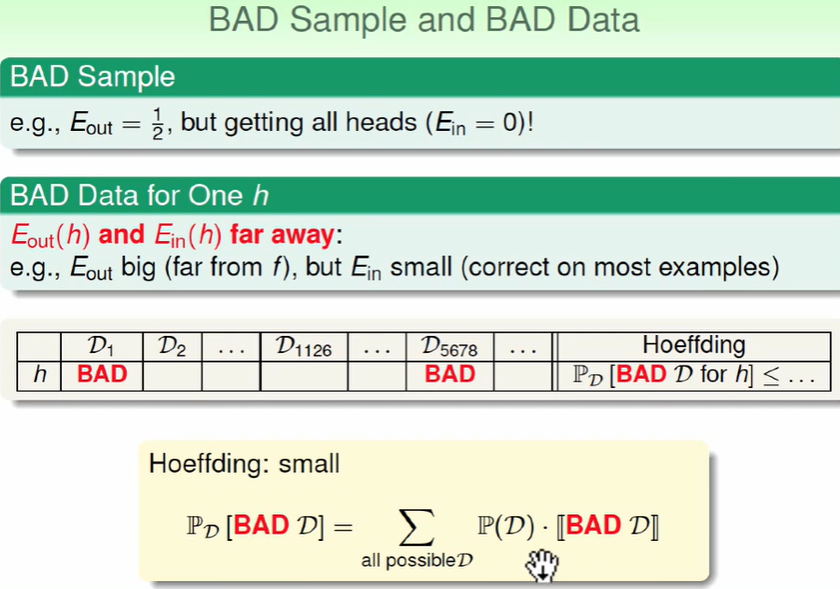
上图的表我们可以看做，抽x个球来估计概率时多少种不同的抽法，得出来的数据有差距时我们认为这就是一个BAD的资料。即$E{in}(h)$和$E{out}(h)$差距比较大时，我们认为这是一个bad的资料。

因此用来训练的资料/数据集 要是比较正确的才可以训练出好的模型。

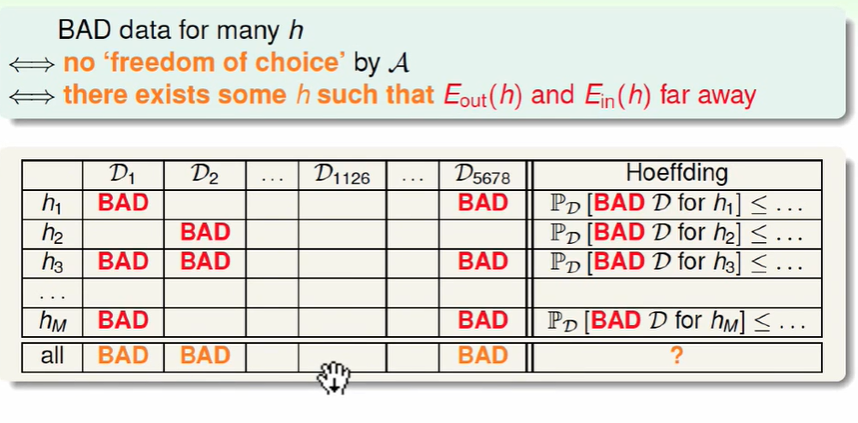
上述列表中D代表着不同的资料/数据训练集， 只要有一个资料对h来说是bad的，我们就认为这个资料为bad的。

因此：

• 要么N大一些，即资料够多，可以进行机器学习。

• 或者我们找到了一个g可以让$E{in}≈0$，那么我们也可以估计到整体$E{out}$也约等于0。那么这个也是一个犯错很少的方法。因此可以进行机器学习。

那么这里我们默认M为finite（有限的），那么对于无限的M呢？如感知机perceptron，这里对应着下一章的内容。