[TOC]

第1章 线性代数中的线性方程组

1.1 线性方程组

线性方程的解有三种情况

• 无解
• 唯一解
• 无穷多解

当方程组有解，我们称线性方程组是相容的。反之无解称之为不相容的。

我们称 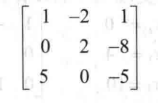为系数矩阵，称为增广矩阵。

解方程的方法：我们可以通过变换先变成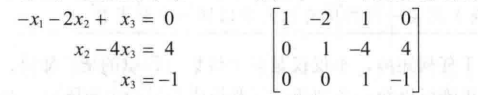

然后通过第三行消去第二行的$x_3$，然后用只包含$x_2$的第二行和只包含$x_3$的第三行消去第一行的$x_2$和$x_3$

最后得到：

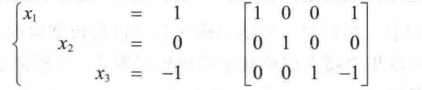
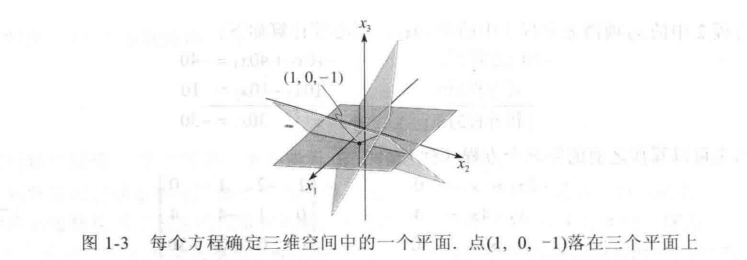
直观理解就是三个平面交于一点，这也是线性方程组的几何意义。

初等变换主要有三种：

• 倍加：把某一行可以以某个倍数加到另一行上
• 对换：把两行对换
• 倍乘：把某一行的所有元素乘以同一个非零数

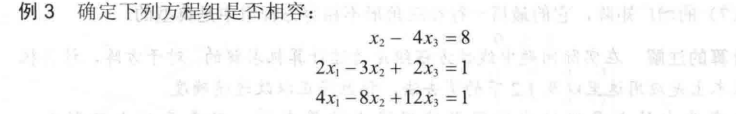
我们通过进行如上提到的变换可以得到：

1.2 行化简与阶梯形矩阵

阶梯型矩阵：

其实就是下面这样的矩阵：

化简阶梯矩阵：

定理1： 每个矩阵等价于唯一的化简阶梯形矩阵

举个例子来说明一下主元位置和主元列的具体意义：

例如上图，我们首先化简为阶梯型

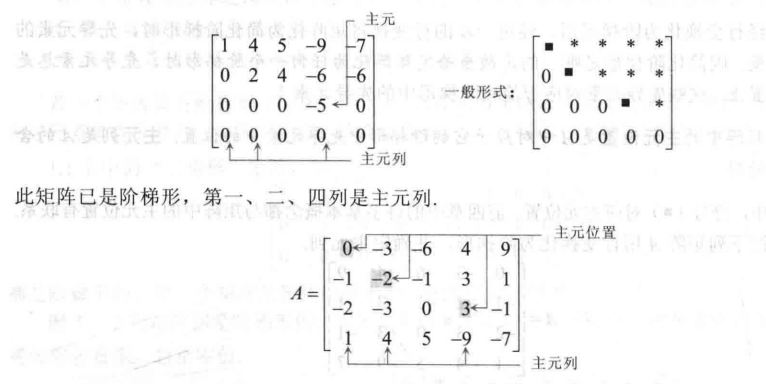
观察上图不难理解主元列就是主元位置所在的列，主元位置就是每行第一个非0的元素所在的位置。

同理：

存在与唯一性定理：

1.3 向量方程

定义：

几何表示：

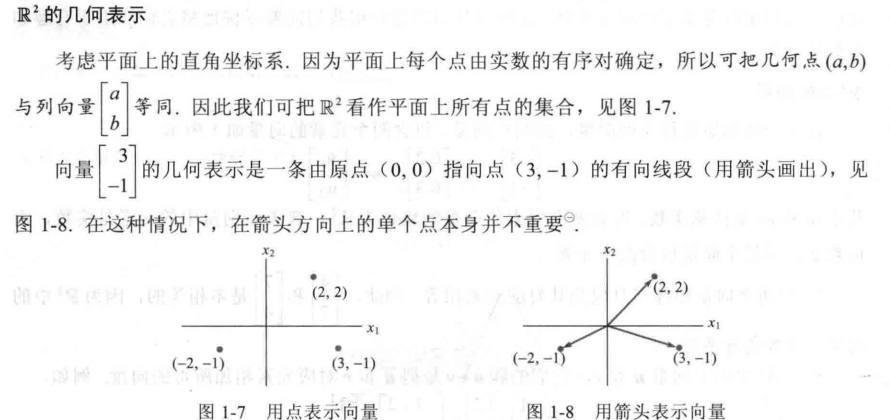
同理$R^3$中的31的矩阵可以看作*立体空间中的向量。

不难发现可以推广到$R^3$

线性组合其实本质也是解方程组问题，如下：

定义：向量组张成的空间中的子集

因此我们判断一个向量是否属于$Span{v_1,v_2,v_3…,v_p}$,我们只需要判断

​ $x_1v_1+x_2v_2+x_3v_3…x_pv_p=b$ 是否有解即可。

不难理解$Span{v_1}$就是一条线 ，$Span{v_1，v_2}$就成为了一个二维平面（当然前提$v_1,v_2$方向即不是相同同，也不是相反，因为符合该条件的两个向量本质是一个方向的东西，并不能张成一个二维平面）

1.4 矩阵方程$Ax = b$

以下四个定义不难理解是等价的：

注意：定理四所提到的等价是A为系数矩阵的情况下，若为增广矩阵$[A\ b]$,则不一定适合，比如若增广矩阵最后一行为 [0 0 0 … 0 4] 那么显然最后一行是有主元的，但是这个方程肯定是无解的，因为 0*x不可能等于4。

Ax的计算方法： 本质就是矩阵乘法的一种特殊情况

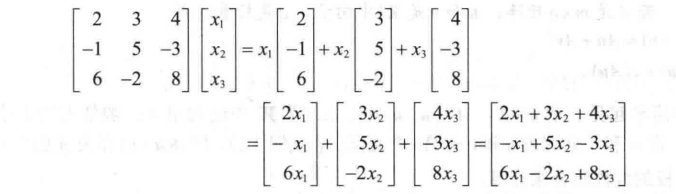
一些显而易见的结论：

1.5 线性方程组的解集

齐次线性方程组：

上面这句话很好理解，如果没有自由变量就说明解就只有一个，也就是说这一个解肯定是那个全为0的平凡解。

因此$Ax=0$的每一个解都是$v$的倍数。

同理：

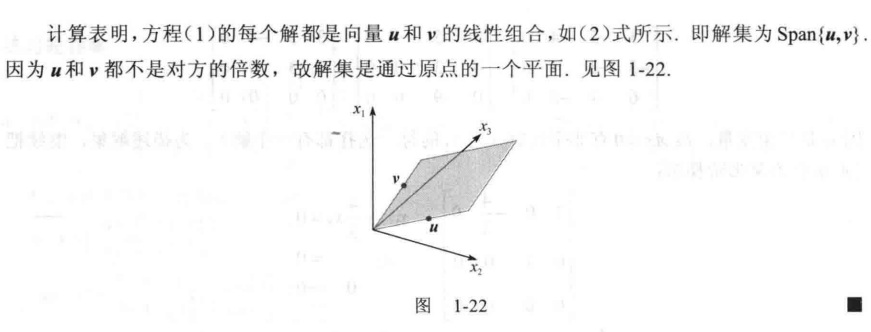
对于这样一个解空间：

我们不难发现这个$x$可以看作 $p$ 的位移，如下图：

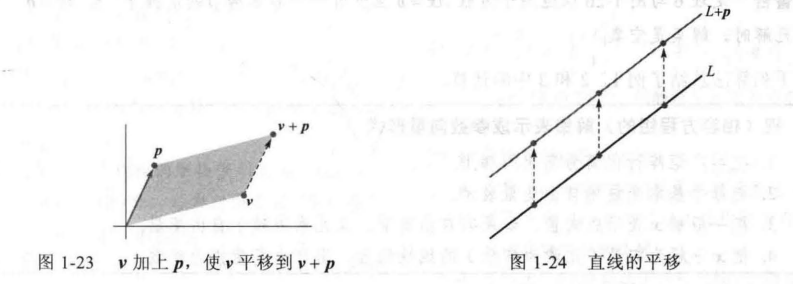
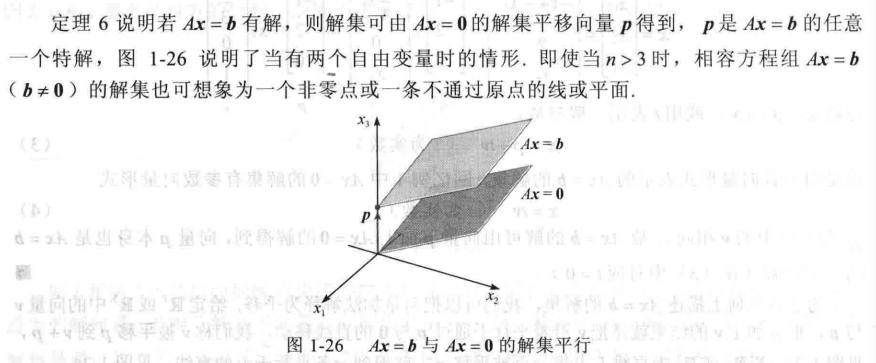
我们不难发现，如果是$Ax=0$, 那么 p这一项消失了就会，但是由于$tv$并不会改变，所以平面方向是不会变的，两个解平面应该是平行的。

注意 : 当然我们上面所讨论的一切建立于方程$Ax=0$至少有一个非零解，我们拆成两部分来看这个非零解：

• 首先肯定是不能无解的，如果是无解就没有解平面了。
• 再看非零这个约束，非零是防止$Ax=0$中出现了平凡解，平凡解没有什么意义，因为$Ax=0$所构造的超平面一定是过原点的。

1.6 线性方程组的应用

这也是体现了本书的特点Application的一章。

以化学方程式配平为例：

这里就不写太多了，都是一些线性代数中线性方程组的application

1.7 线性无关

第一问很简单，我们扔进$Ax=0$看看有没有解即可，即增广矩阵变换一下算出解即可。

b. 因为$x_3$为自由变量，直接随便带入一个即可。

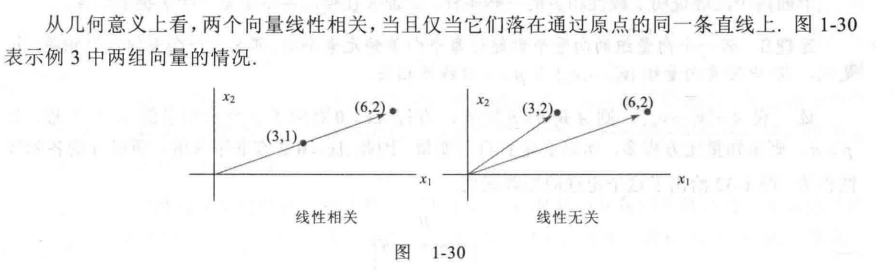
两个2维向量a,b构成的向量组线性相关的几何意义是: a,b共线
三个3维向量a,b,c构成的向量组线性相关的几何意义是: a,b,c共面/a,b,c共线

不难发现： n个向量所张成的空间维度小于n，那么这n个向量就是线性相关的。

也就是说：

​ 其实不难理解，为什么n个向量所张成的空间维度小于n呢？因为有些向量是“假的”，它可以通过其它来的向量来表示，也就是说这个向量可有可无，这样n个向量就会变成n-1，张成空间的维度显然会下降。

一个显而易见的定理：

直观理解就是一个零向量其实是可有可无的，因此维度自然会下降，因此n个向量所张成的空间维度小于n，那么这n个向量就是线性相关的。

这个定理通过构造达到了线性相关的定义，本质还是如下定理：

1.8 线性变换介绍

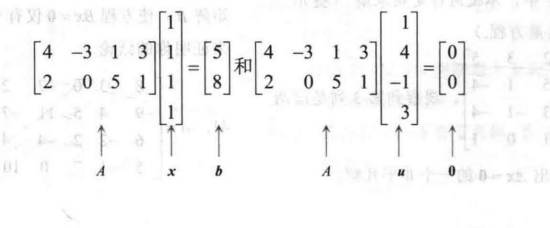
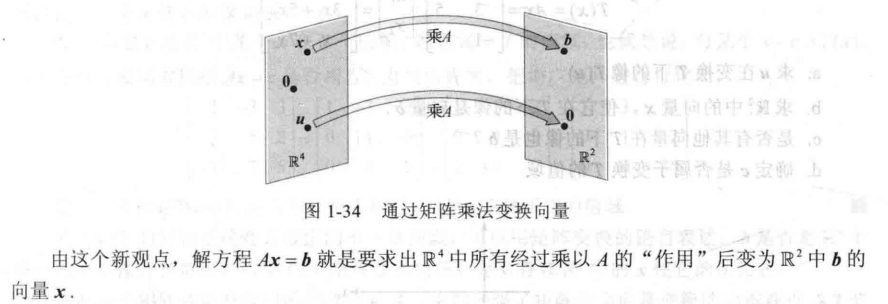
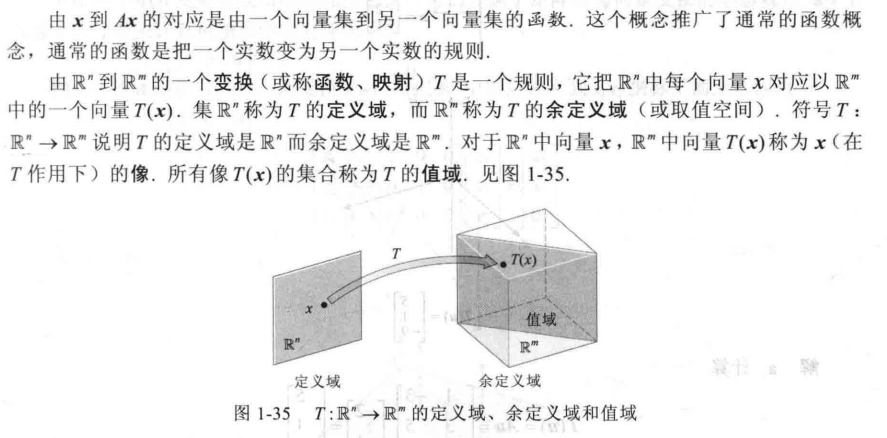
我们看一个几何意义：

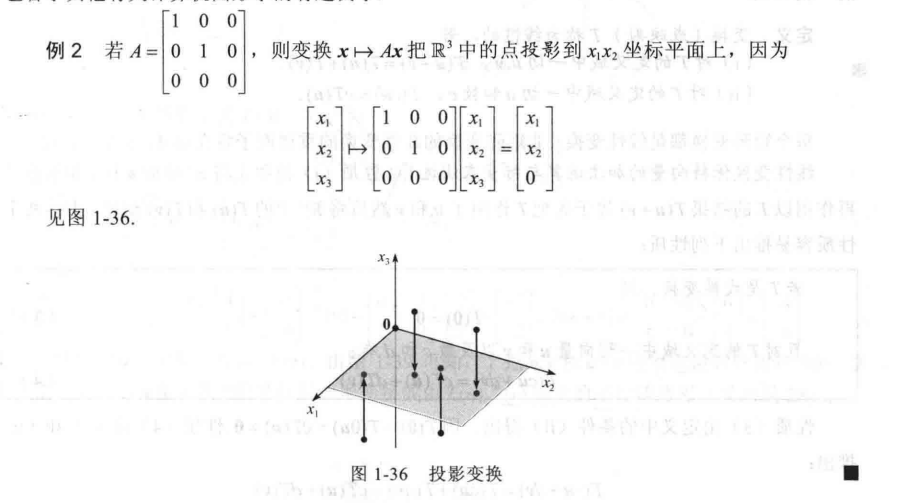
这个也属于计算机图形学的矩阵变换的内容。

线性变换：

推论：

图像旋转（同样属于计算机图形学的内容）：

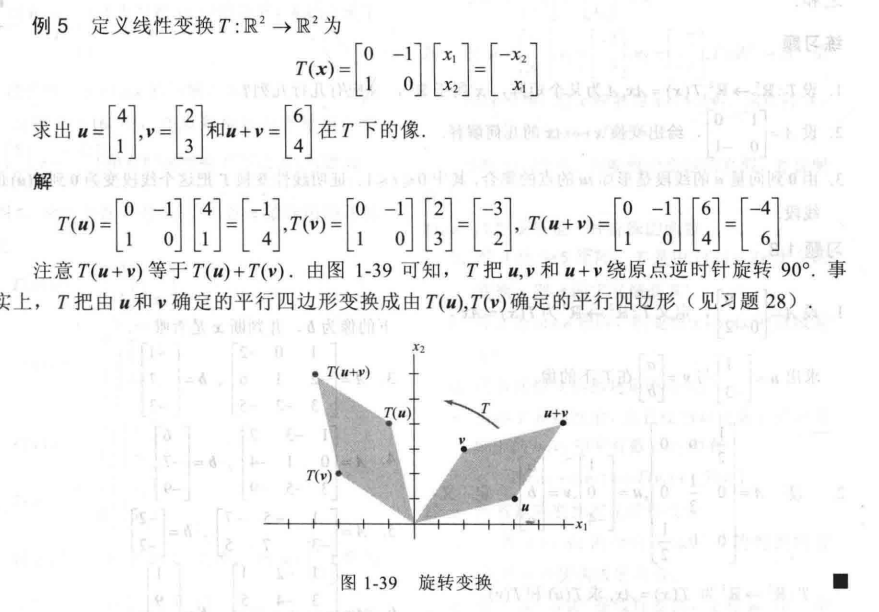
1.9 线性变换的矩阵

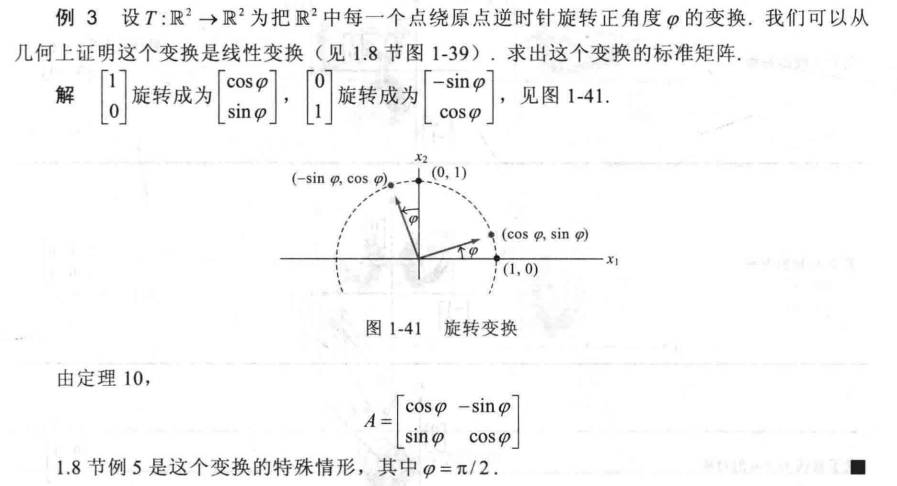
$R^2$中的几何线性变换

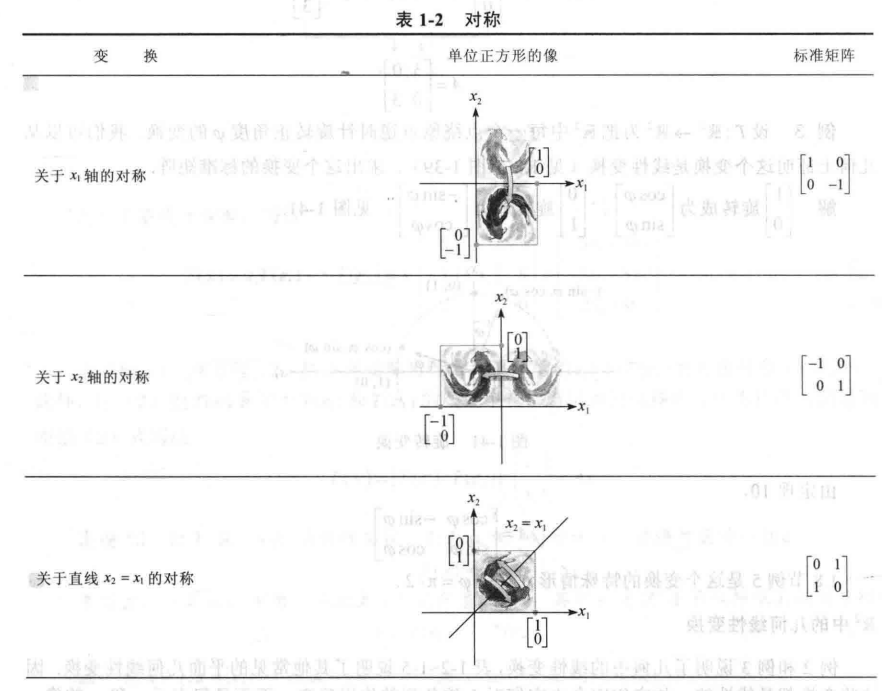
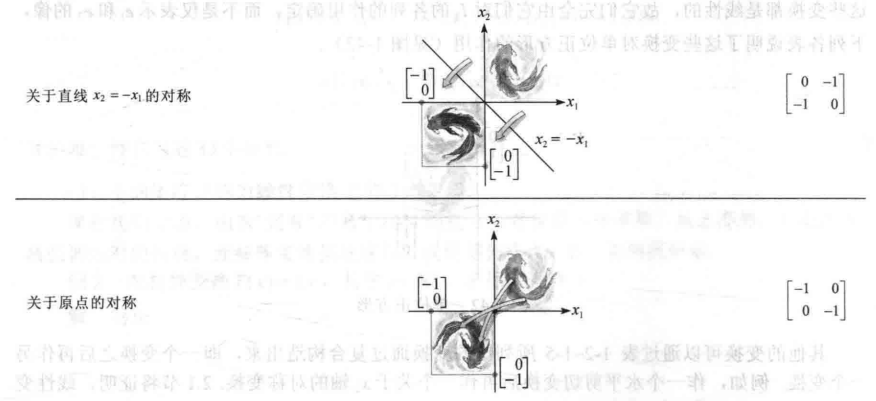
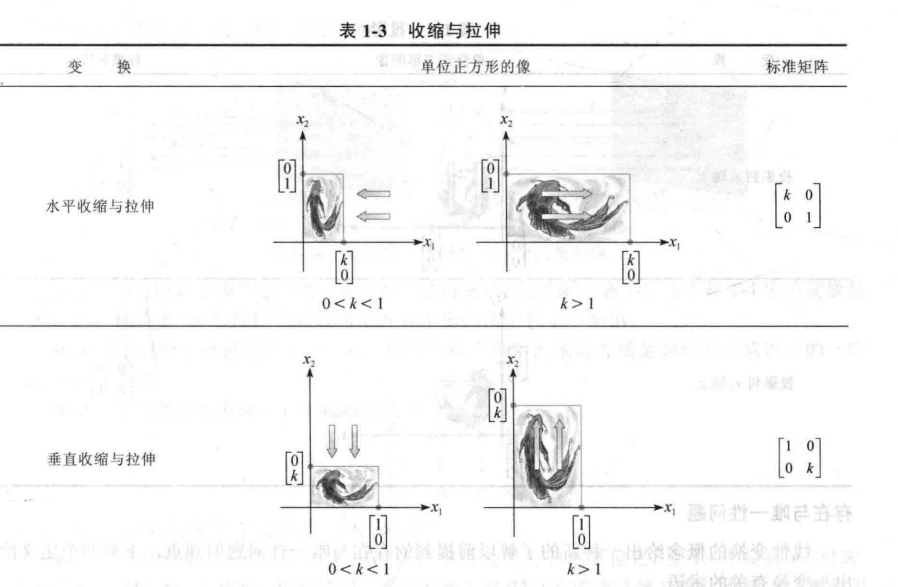
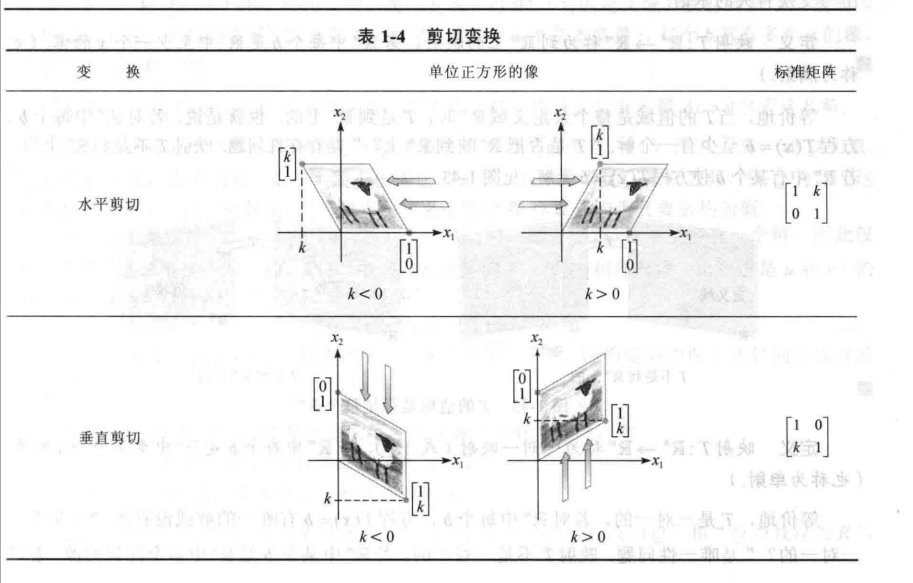
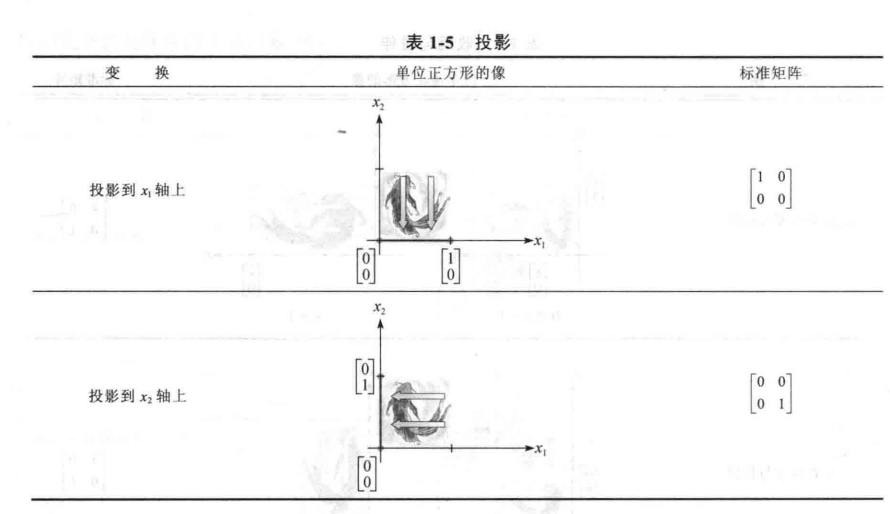
总结一下：

这一小节一直在讲映射的问题，其实也是一个降维的问题，比如A 是一个3*4的矩阵，x是一个4*1的矩阵，Ax变换后成为了3*1的向量，这是一个降维的过程。但是者可以称之为一个很好的降维方法吗？如果多个4维向量都映射到了同一个三维向量，那么这种不是一对一的映射（单射）是不够优秀的，因此比如：

这个矩阵是有自由变元的，也就是说$Ax=b$ 时，一个b会因为自由变元使得多个x都映射在b上。