CH7: The VC Dimension

Definition of VC Dimension

上述推导就是VC bound带入了$m_H(N)$的范围。

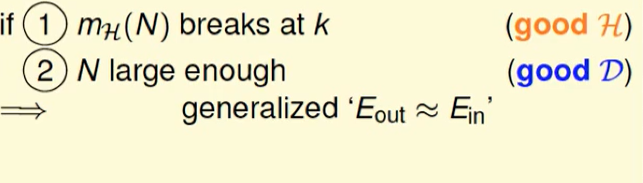
因此我们需要什么可以使得$E{out}$和$E{in}$近似呢？

• 一个好的$H$,也就是growth function要有break point ，即$m_H(N)$在k处break
• 一个好的$D$, 也就是说N要足够大

要想可以机器学习，不仅要$E{in}=E{out}$ 也要$E_{in}$贴近于0

要$E_{in}$贴近于0，也就是说我们要有一个好的演算法。

---

VC Dimension定义：

这个其实就是$break point - 1$.

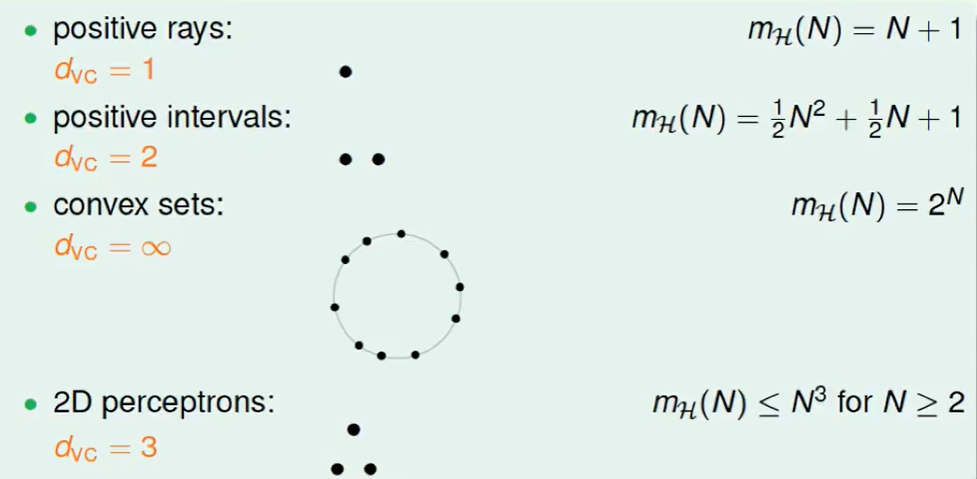
所以现在我们原来认为 有breakpoint的是好的hypothesis，那么现在我们换一种说法：

$d_{VC}$是有限的.

$d_{VC}$是有限的保证了以下的事情：

这道题的答案我们会误以为是3，但其实是4，因为$d_{VC}$ 对任何一笔资料都不能shatter才能说是3，但是题目中只是一种资料。

VC Dimension of Perceptron

以二维的PLA算法来看：

最后不难想到：

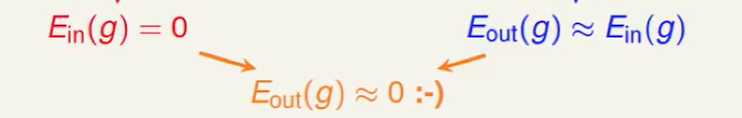
那么对于多维的PLA算法：

我们从1-D 2-D就做出这种假设并不是很聪明，这很有可能是巧合：

因此证明我们分两个部分：

• $d_{VC}\ge d+1$

  证明这个只需证明：

  即存在d+1个的inputs 可以shatter，即$d_{VC}$肯定>=d+1,因为如果小于d+1，那么任何数据集都不能出现shatter。

  

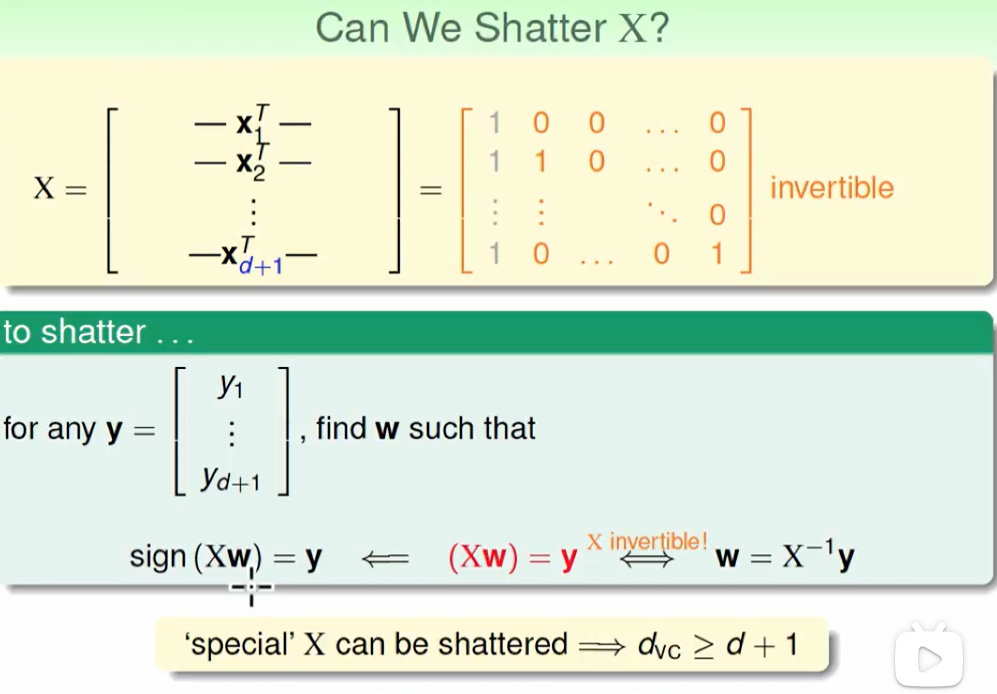
  上面这个怎么理解呢？

  对于任意一种预测结果$y$，我们都是通过这样的方式算出来的$y$, $sign(Xw) = y$

  y可以搞出来各种排列组合的结果，现在我们只要证明真的存在这样一个$w$使得公式成立即可。而因为X恰好是可逆的：

  

  因此$w = X^{-1}y$ 公式恒成立，故证明完成。

• $d_{VC}\le d+1$

证明这个只需证明：

physical intuition of VC Dimension(直观的物理意义)

​ 根据之前的推导就将VC Dimesion和d+1维的perceptrons联系起来了。上节中公式里的W称为自由度，自由度如同旋钮一样可以进行调节，就可以有无限种hypothesis（每个旋钮都有无限种可能性），VC Dimesion的物理意义就是hypothesis set在二元分类中的有效自由度。

​

VC Dimension就是hypothesis的最大分类能力，最多能shatter的输入数量。

可以使用旋钮的数量来大概估计VC Dimension。

如上图，只有一个旋钮a ，VC Dimension=1

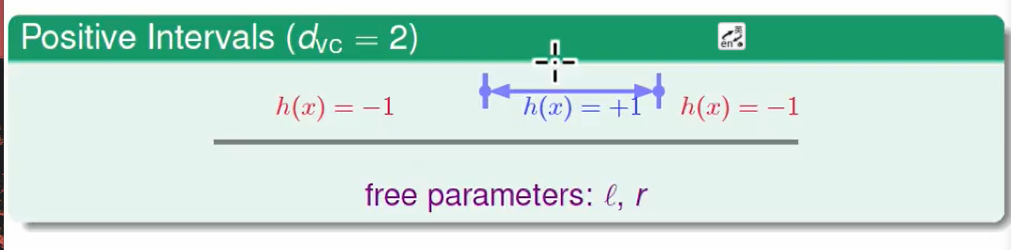
两个旋钮 l 和r ，VC Dimension=2

因此我们提出：

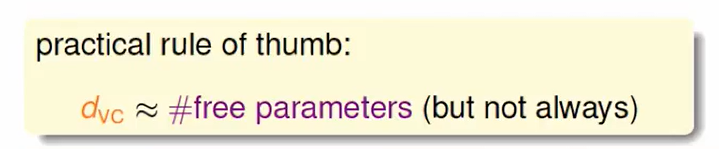
看看有几个可调的旋钮，这是一个很好的大概估计方式，但不是一个always 准确的方法。

---

interpreting VC Dimension(深入理解)

首先回顾一下VC Bound的公式

我们不妨设$\delta$ = 右边一串式子。

VC bound的意义我们可以取他的相反面，本来描述的是坏事情发生的最大概率，我们现在反过来求好事情发生的最小概率，即：$E{in}$和$E{out}$ 差距不大（GOOD）时，概率是大于$1- \delta$的。

最后我们首先推出来 $\epsilon$的表达式，那么现在：

可以改写为：

即代表：我们举一反三(模型泛化 或者说是 in和out有多接近)做的有多好

我们把不等式绝对值去掉：

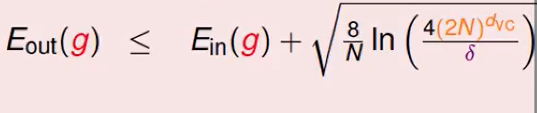
这个公式说明了 ：根号下的这个东西 是和hypothesis或者说是提出的model有关的，这个可能非常强，模型很复杂可以处理高维plane，但是我们在generalization的时候要付出代价(即E的in和out差距比较大)

所以VC Bound在告诉我们以下的事情：

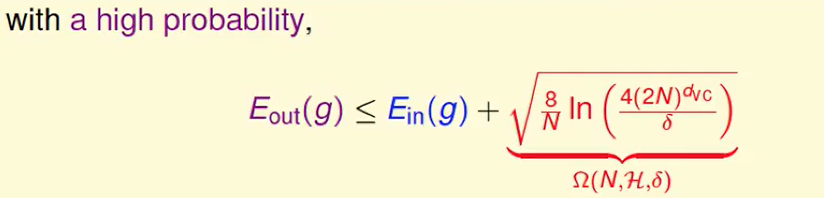
我们画一个图来看这个问题：

VC Dimension较小，此时$E{in}$ （即你所说的 根据已有数据计算出的风险）会变大的，这是因为shatter的点会变少，点的排列组合会变少找到一个比较好的hypothesis的概率也会比较小，那么$E{in}$就会变大。 所以我们真正要找的是一个合适的VC Dimension，来使得$ E_{out}$ 变小。

---

一般资料数是10倍的VC Dimension即可就可以获得一个不错的表现。

那么我们就会奇怪了，理论算出来是10000倍，为什么实际上怎么就需要十倍左右呢?

这是因为VC Bound 得Looseness. 他的宽松(Looseness)是因为下面四个原因。