CH8: Noise and Error

[toc]

Noise and Probabilistic Target

我们之前对于机器学习的流程如下图：

那么在加上noise后是否会影响机器学习呢？

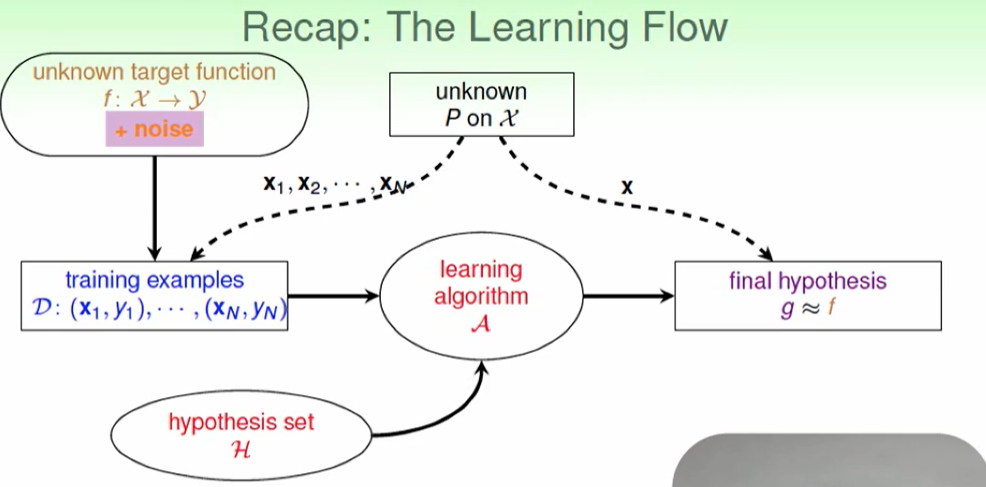
原来的瓶子里抽弹珠是确定的，即输入x，出来就是f(x) ：

现在出来可能有一些不是f(x)了，即出现了噪声：

但是这并不影响我们估计一个。

那么：

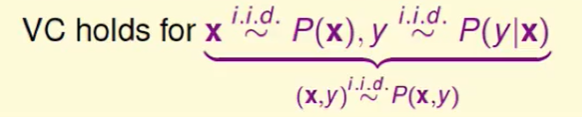
VC Bound依然适用。

---

我们以前的机器学习都是target，而今天是一个target distribution，即一个目标分布。

target distribution的看法

• 在这里他把distribution看作是 最理想的目标函数和 noise 的组合(0.7 + 0.3)，所以我们把0.7当作target，然后我们会犯30%的错误。

新的learning flow：

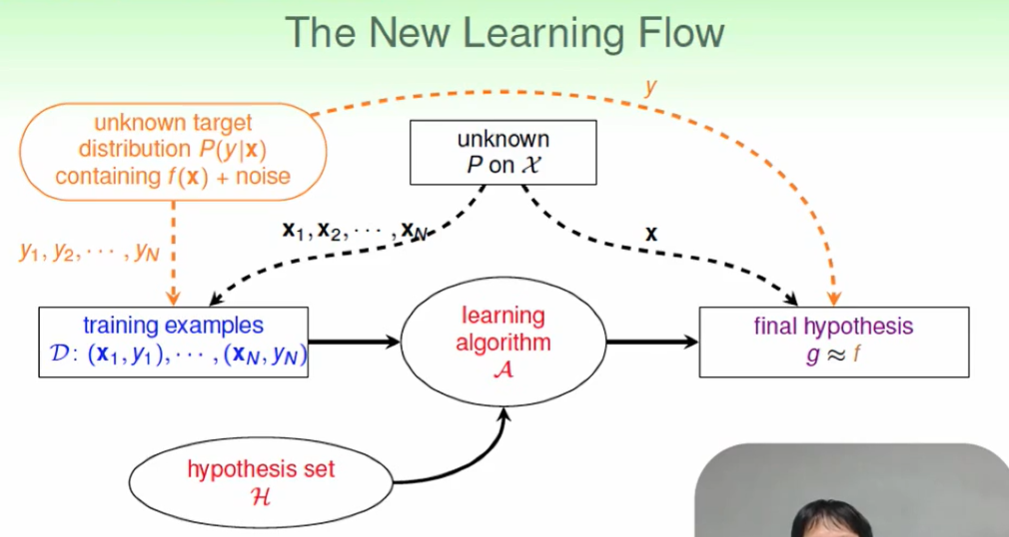
Error Measure

错误率的计算方式：

• pointwise error measure

  这个就是每个都测一遍，然后统计一下错误率，这也是最常用的。

  

• two important pointwise error measure(分别是0/1 error 和 squared error)

  

举一个0/1 error 和 squared error的区别：

可以看出不同的错误测量的准则会影响我们选取的结果。

加上error measure 的leaning flow

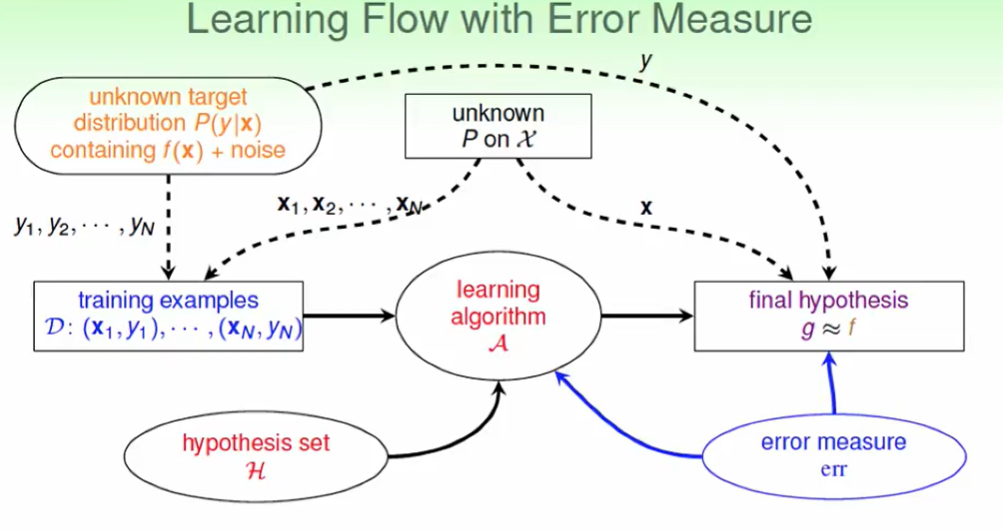
Algorithmic Error Measure

不同的错误方式：对于指纹系统其实是无所谓的，因为我们只需要知道可以不可以进去就OK了，而不在该进去的进不去，不该进去的进去了，这都是致命错误。

​ 但是在超市应用时，两种错误会影响未来的生意：比如我该有折扣，但是因为系统错误没给我折扣，这回lose future business。但是我不该有折扣但是给了我折扣，超市在不亏钱的情况下还收获了跟好的口碑。所以这两者的错误权重不能看作相同的。

不妨设置为某个数倍的错误：

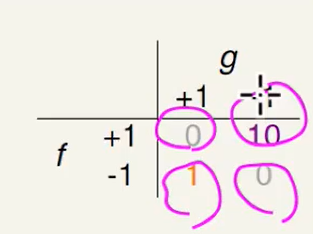
但这上面这个错误的衡量方法就一定是10吗，为什么不是100，因此我们在做系统时非专业的人很难给出这个倍数的大小。我们后面会更详细的讲下面这个错误度量方法。

Weighted Classification

现在我们改写了$E_{in}$的衡量方式，那么会影响我们之前所提到的 分类问题 吗？

首先是PLA：

PLA是无所谓的，因为他最后一定是没有错的，权重对他来说没什么用。

那么如果不是线性可分的呢？

还是可以用pocket算法，从 原来的比错误个数 改为 比错误权重和，这样合理吗？

证明：我们可以这么改写错误的点，对于1000权重的错误，我们可以看作 1000个权重1的错误在同一点，因此这太符合pocket算法了。