《线性代数及其应用》CH2：矩阵代数

[toc]

第二章 矩阵代数

2.1 矩阵运算

对角矩阵，零矩阵定义：

矩阵与标量的乘法：

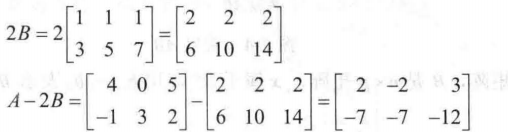
一些矩阵乘法的相关性质：

矩阵转置：

转置的相关性质：

前三个很简单，最后一个证明从定义入手：

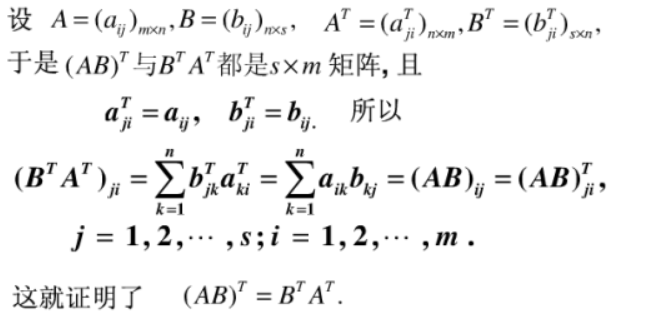
2.2 矩阵的逆

矩阵可逆：

  • 不可逆矩阵 = 奇异矩阵
  • 可逆矩阵 = 废弃及矩阵

判断矩阵是否可逆：

方程唯一解 与 矩阵可逆：

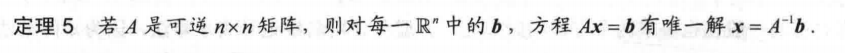
c.证明：

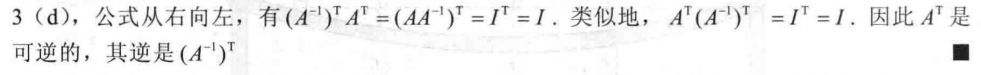
初等变换 的等价:

对于一个单位矩阵I, 我们进行初等变换为 I’, 然后再和 矩阵E 相乘 等于I′E, 这个等价于直接对E做同样的初等变换。

例如：把单位矩阵的第一行的-4倍加到第3行，得到：

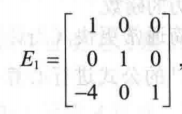
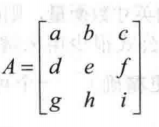
然后再和矩阵A相乘得：

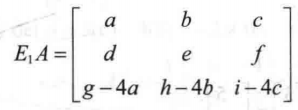
我们观察这个矩阵其实和A直接做初等变换是一样的，都是第一行的-4倍加到第3行。

这个性质可以求逆：

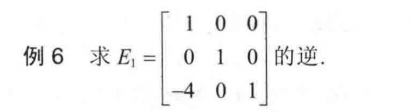
我们想让E1 乘一个矩阵边为单位矩阵，那么可以让矩阵为 第一行的+4倍加到第三行就变成了单位矩阵了，这可以利用上面那个性质。

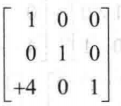
这个矩阵相当于对单位矩阵做了第一行的+4倍加到第三行的初等变化，那么乘上E1 就相当于E1做了 初等变化（第一行的+4倍加到第三行的初等变化），从而变成了单位矩阵，那么E1 的逆就是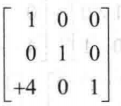

这也就对应上了这个定理：

简单理解就是一个矩阵如果可以经过初等变换变成单位矩阵，那么他就有逆，且他的逆就是 单位矩阵乘上那些初等变化矩阵。

因此我们此时就可以提出求矩阵逆的算法：

这个很好理解，还是上边的意思，只不过通过矩阵这种形式化的数学语言做了简要概述，对于一个矩阵A，我通过初等变化变为了单位矩阵，说明对单位矩阵做同样的操作，这个就是A的逆矩阵，

求矩阵逆的算法的例题：

2.3 可逆矩阵的特征

证明上述定理只需要证明下述的这个环即可：

2.4 分块矩阵

首先是一些基本计算和普通矩阵是没有区别的。

分块矩阵基本运算：

分块矩阵的逆：

不妨设：

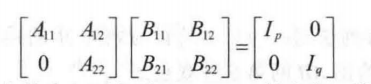
列出方程：

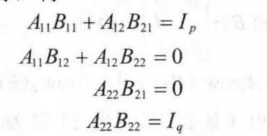
得到：

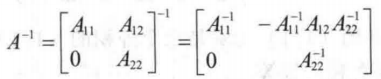
知道怎么来的即可，分块求逆有很多公式，对应着不同的情况。

2.5 矩阵因式分解

LU分解：

对于这样的一个问题

我们可以一个一个的求解。

当然，如果A可逆，也可以先算A−1, 然后直接算x=A−1b,即可算出解。

我们首先可以解Ly=b 这个方程得出y,然后算 Ux=y , 解出x, 同时我们注意到由于L,U都是三角矩阵，很容易就可以解出来方程。

LU分解算法：

L的计算方法很简单，我们在上述将A变成阶梯型矩阵U的过程中，我们就是把每一列

2.7 计算机图形学

这个在博文《AHU计算机图形学》有详细的解释

2.8 Rn的子空间

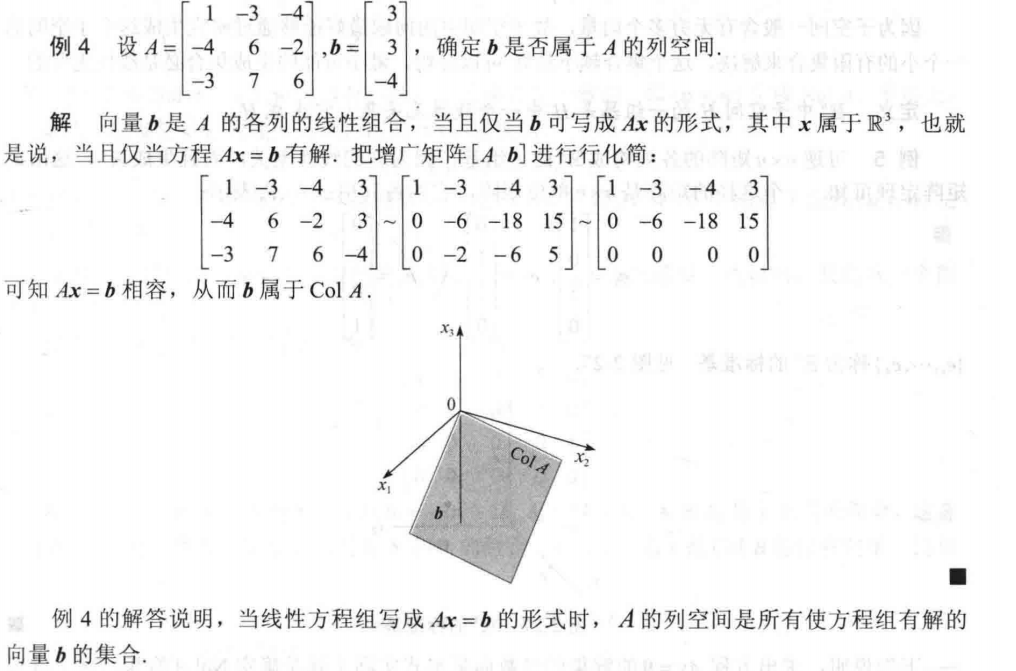
矩阵的列空间：

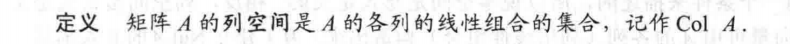
矩阵的零空间：

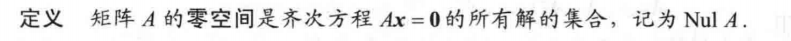
子空间的基：

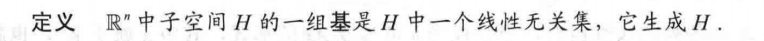
标准基

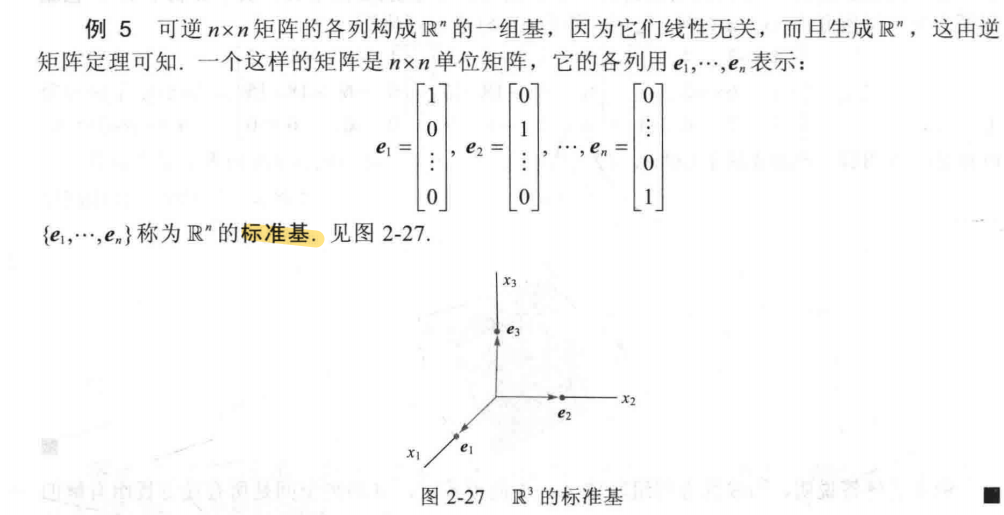
零空间Null A 其实是保证了它一定是矩阵的基。

我们可以直接找主元列作为列空间的基，即下面这个定理：

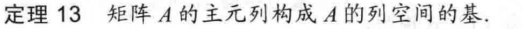
2.9 维数与秩

矩阵的秩：

我们一般称子空间的维数为秩：

秩与可逆矩阵定理 ：