CH10：Logistic Regression

Logistic Regression Problem(逻辑回归)

我先我们看两个例子，看一看 他们的不同：

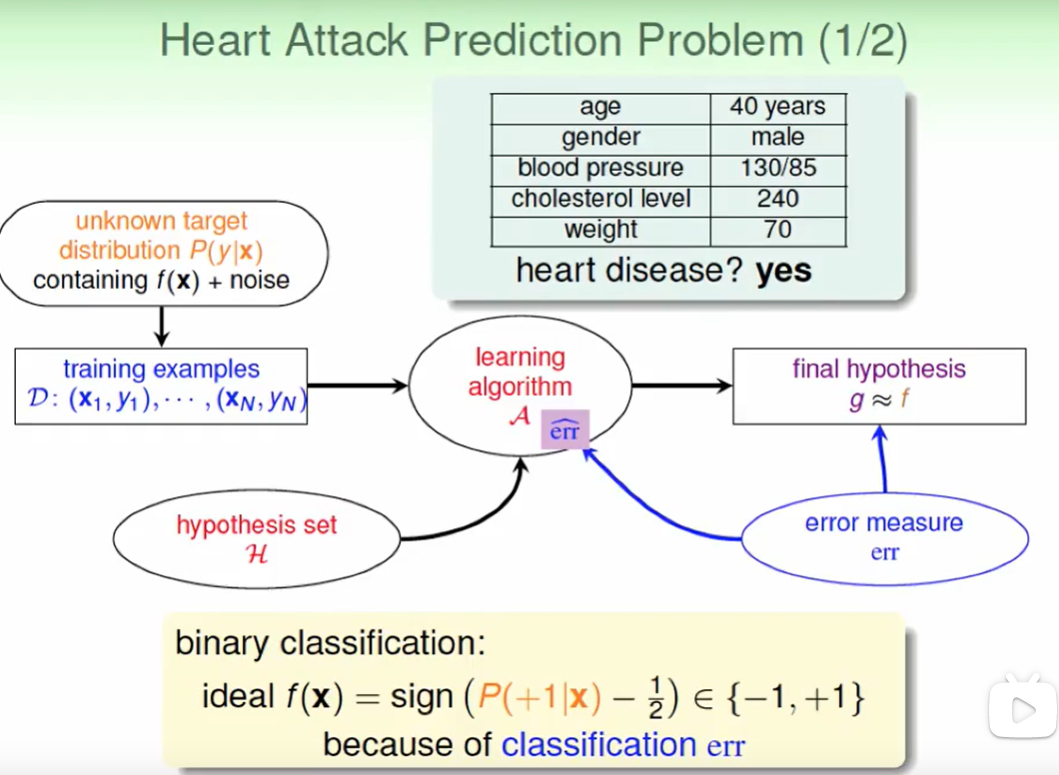
根据一些指标来预策是否会有心脏病, 很明显是一个分类的问题，我们关心的是错误率为多少。

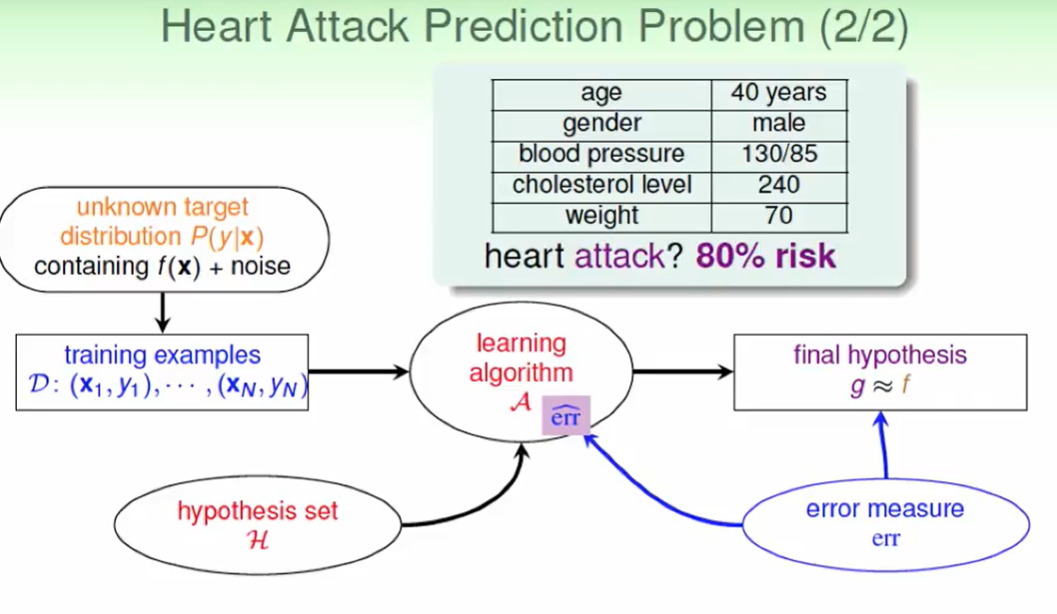
再看看看这个问题，求心脏病出现的可能性。

这不在是一个简单的二元分类问题，而是需要给出概率，我们称之为：

soft binary classification

---

我们希望得到这种数据：

告诉我们不同的病例，然后给一个得病的几率，然后我们去做linear regression就好了，可是现实中这个概率是不可能知道的。

但是现实中我们只有这种普通的病例资料：

即在知道病人身体状况的情况下，这个病人是否患有心脏病，但是这个患上的概率只有上帝才知道。

---

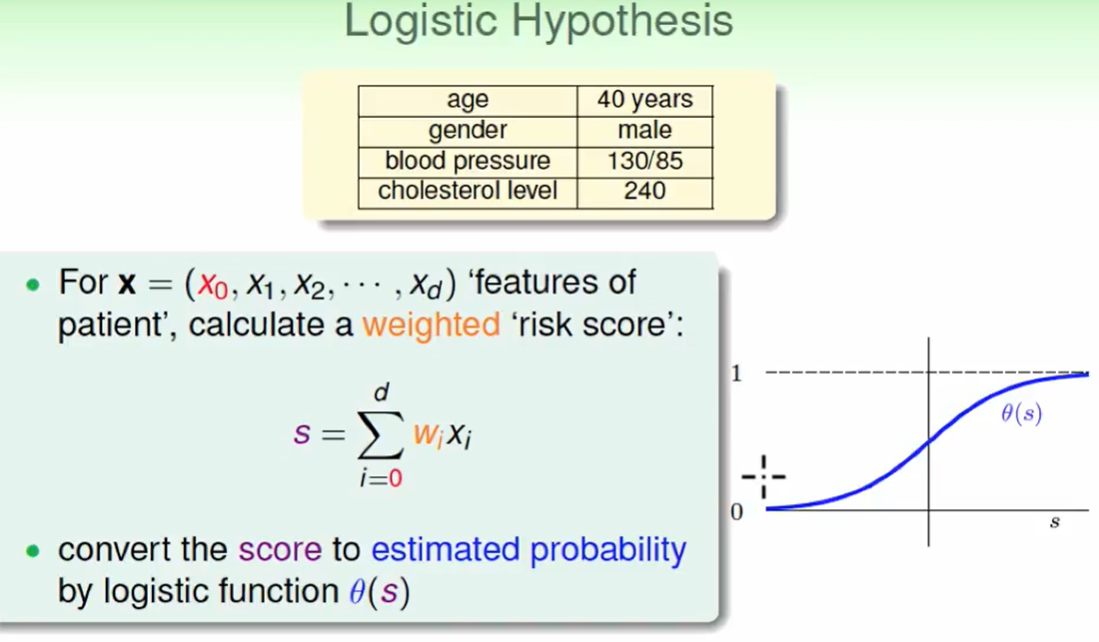
​ 我们想到，可以这么来做：首先计算一个 $w$ 权重向量，然后我们用这个权重算一个分数出来（即上图中的$s$）， 我们用这个得分再通过$\theta$ 函数来等价转化为概率。

即：logistic hypothesis

其中的 $\theta$ 函数我们称之为Logistic Function:

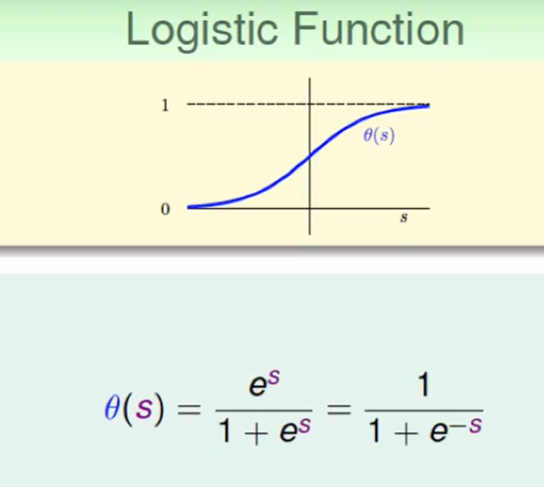
所以logistic regression就是在做下面的事情：

Logistic Regression Error

---

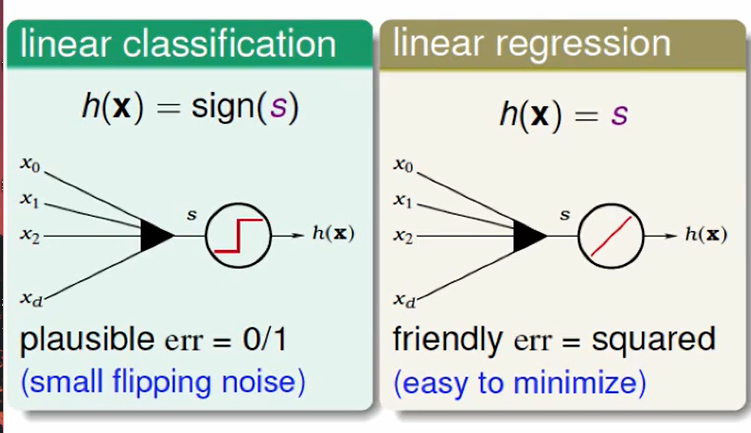
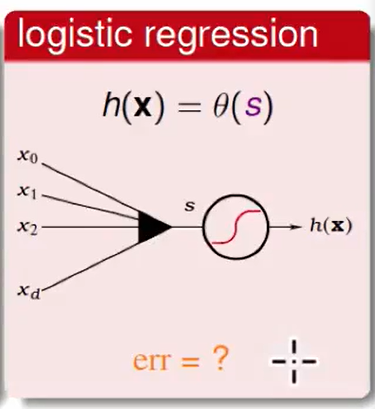
三个放在一起我们很容易就发现他们的区别是是error measure的不同。

那么我们如何定义logistic regression的error measure呢？

---

首先,target function是长如下样子的：

考虑换一下后半项为：

我们假设h可以产生相同资料：

如果h和f很接近，那么$h$和$f$产生同一批资料的几率很接近。

所以我们现在想要做到：

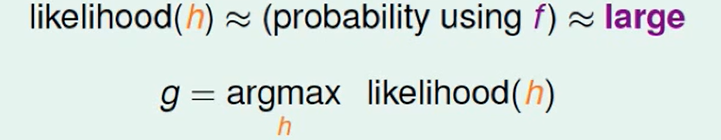
让$h$最大程度的接近$f$。

同时我们注意到$h(x)$的一个性质：

定义likelihood为：

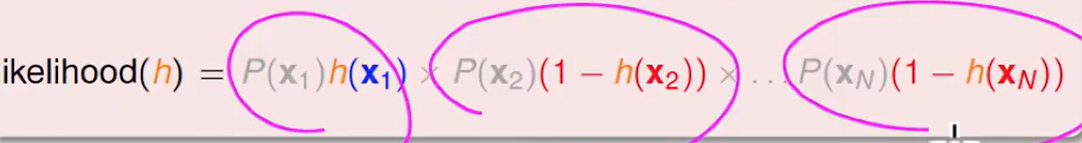
我们可以把$1-h(x)$换掉,即：

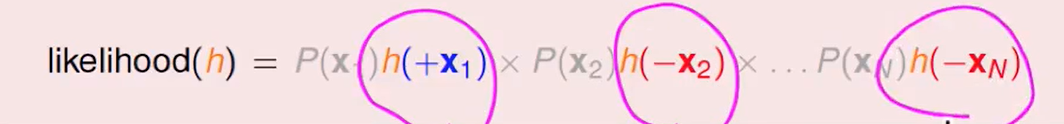
所以这个函数正比于h对于每笔资料的连乘：

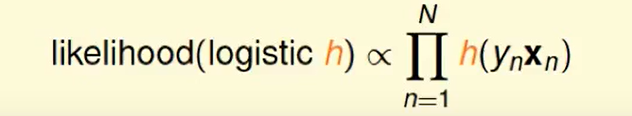
所以我们想找一个$h$使得likelihood最大。

还记得：

我们替代一下，即求w即可：

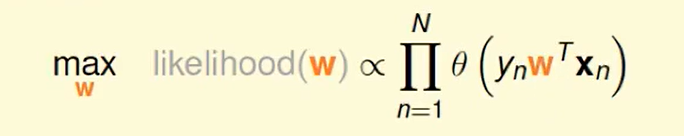
我们想把连乘-> 连加，那么取ln即可：

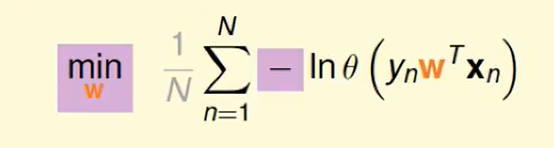
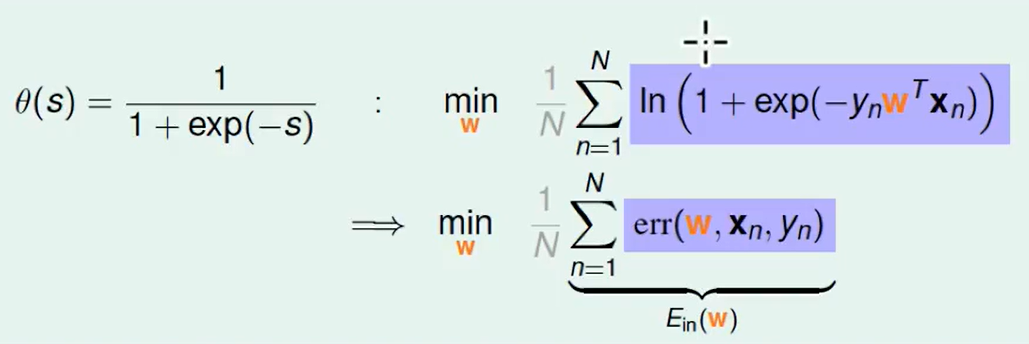
交叉熵(cross-entropy)

Gradient of Logistic Regression Error

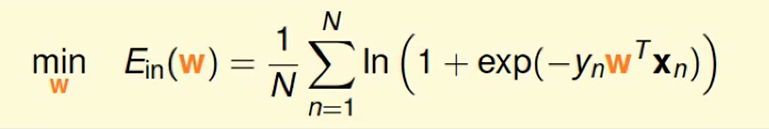
还是要求梯度：

即：

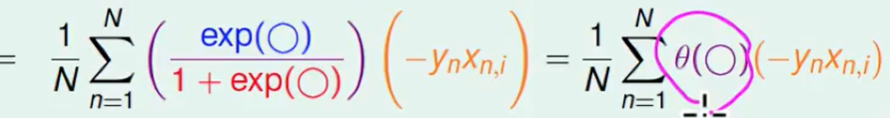
我们想让这个梯度等于0

• 如果所有的$\theta = 0$，说明$y_nw^Tx_n>>0$, 翻看前面PLA的内容，这个说明了全部做都正确答案了，即 数据是线性可分的。
• 反之，我们就需要解这个方程了，且说明了不是线性可分的，不巧的是这个方程很难解，我们需要一些别的方法找出解。

我们回顾一下PLA：

我们把上面两个可以写成一个式子：

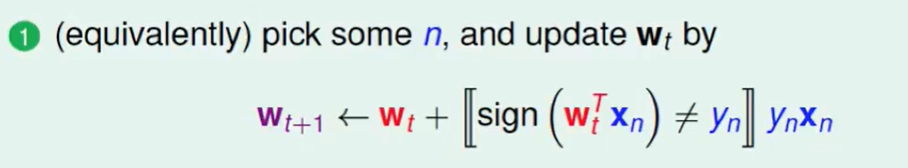
也许我们可以用PLA类似的方法更新来迭代出梯度=0的点。

Gradient Descent

迭代最优化（iterative optimization）

这个$v$, 是纠错的向量，这个$η$ 是修改的步伐的大小。

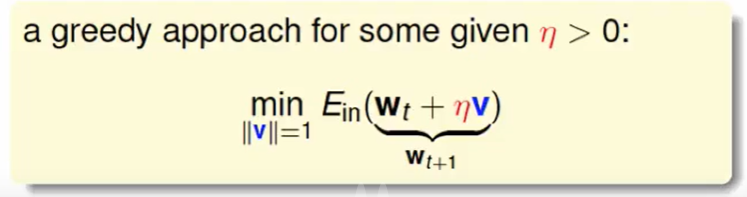
我们把Ein拆开，可以得到下面近似等式，这其实就是当$η$足够小的时候的一阶泰勒展开。

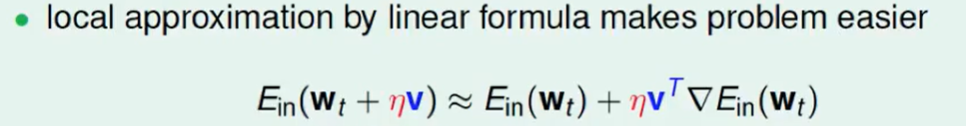
我们现在就要规定$v^T$ 的方向，怎么才能让他最快到达底部呢？很容易沿着梯度相反的方向，即：

即这样更新：

---

$η$ 的选择：

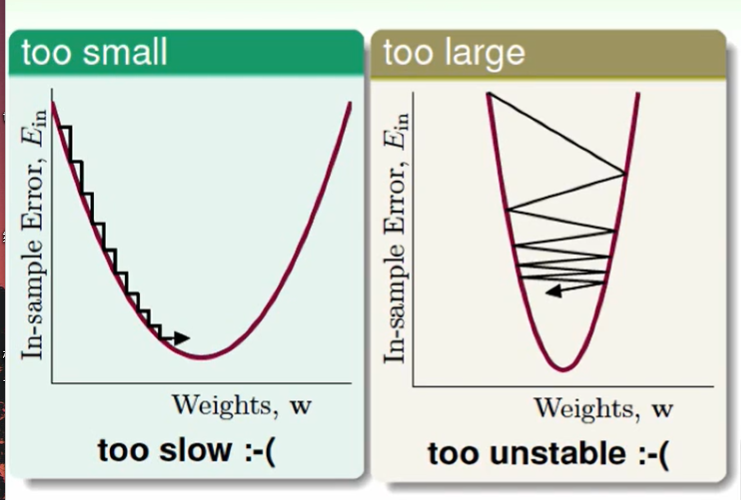
坡度大，跨的大一点，坡度小，跨的小一点。

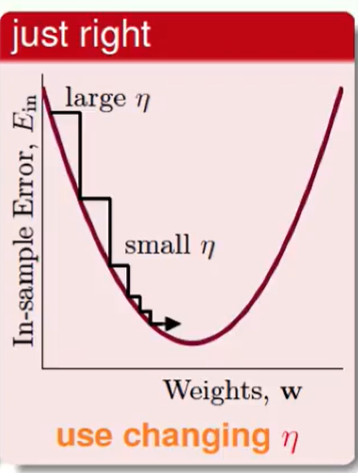
上述说明：$η$和梯度的大小正相关是比较好的：

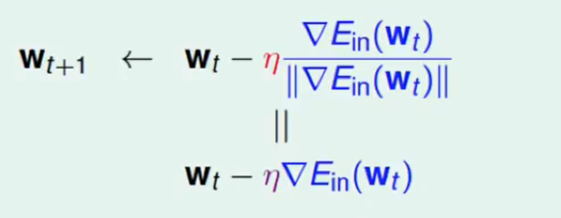
我们称紫色的η为：fixed leaning rate

所以我们现在更新的方式是：

因此逻辑回归算法就是：

这样不断迭代，就会找到一个$w$ 使得这个 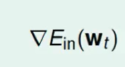等于0。

还记得我们为什么要求这个w吗？

h(x)也就是给出一个身体情况，我们就可以求出他的心脏病的概率，这个$h(x)$的公式如下：

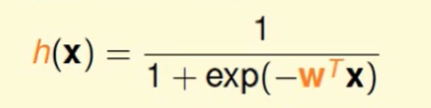
这里面的$w^T$是要求出来才能用这个公式, 到此为止 我们的问题就解决了。