CH12：Nonlinear Transformation

Quadratic Hypotheses（二次假设）

Linear Hypothesis

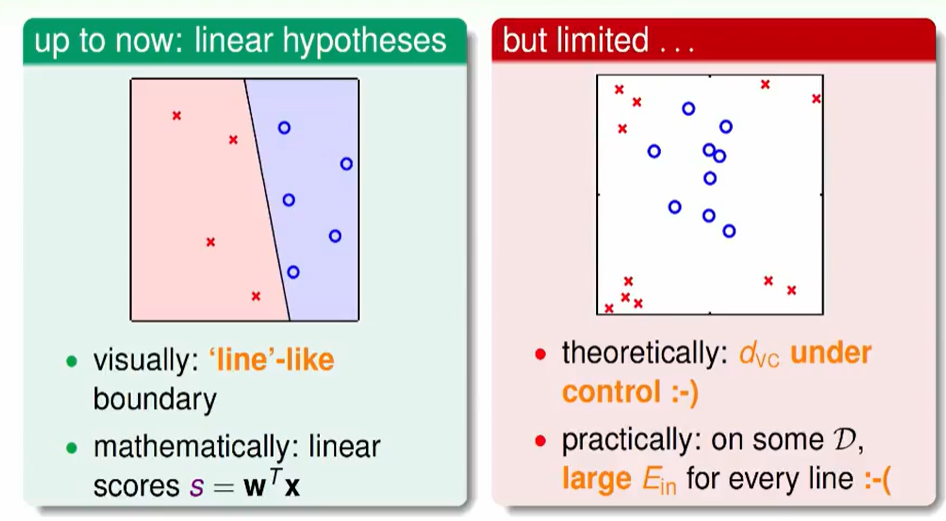
线性模型可以算一个分数，它最大的好处是$d_{VC}$ 可以被控制，当然线性模型在某些数据上每条线都做不到效果很好。

---

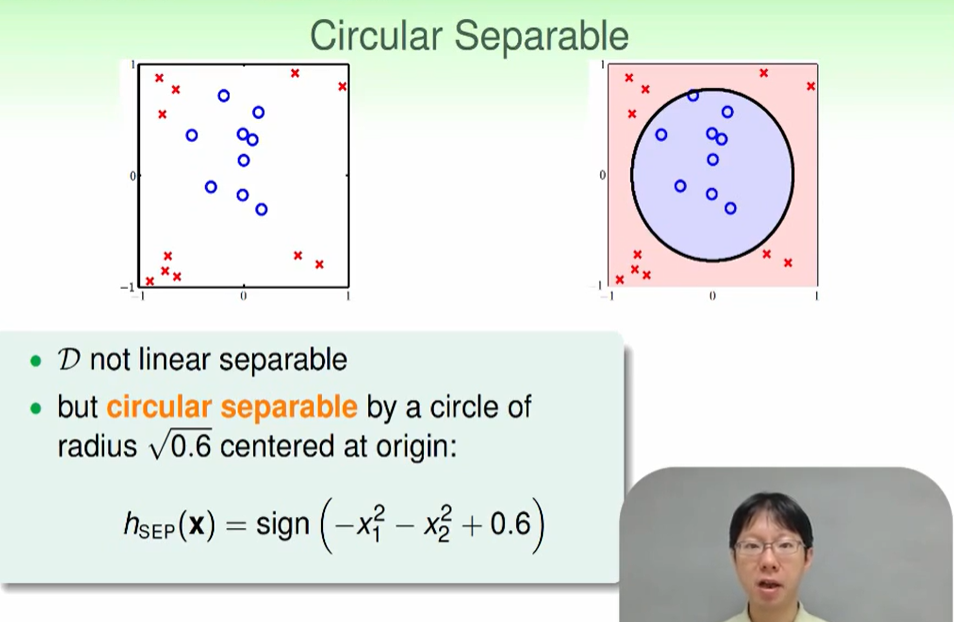
我们这里用一个圈就可以很好地进行分类。

那么我们可以设一个圆形的PLA,可是图形是千变万化的，我们不可能每个都设计出来一个PLA，那么我们可以系统化的设计一个。

我们可以把式子化为：

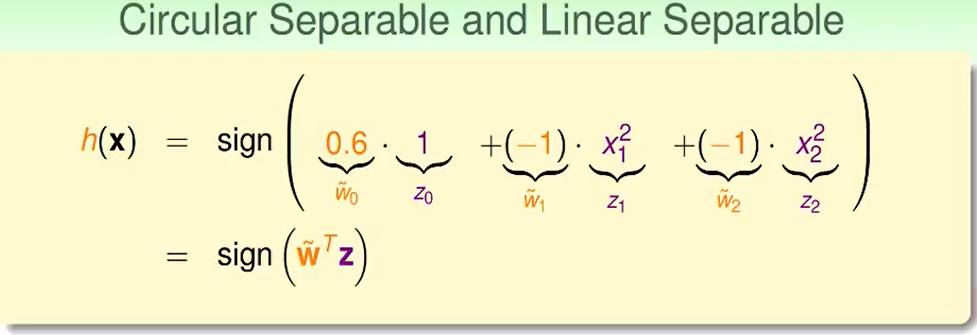
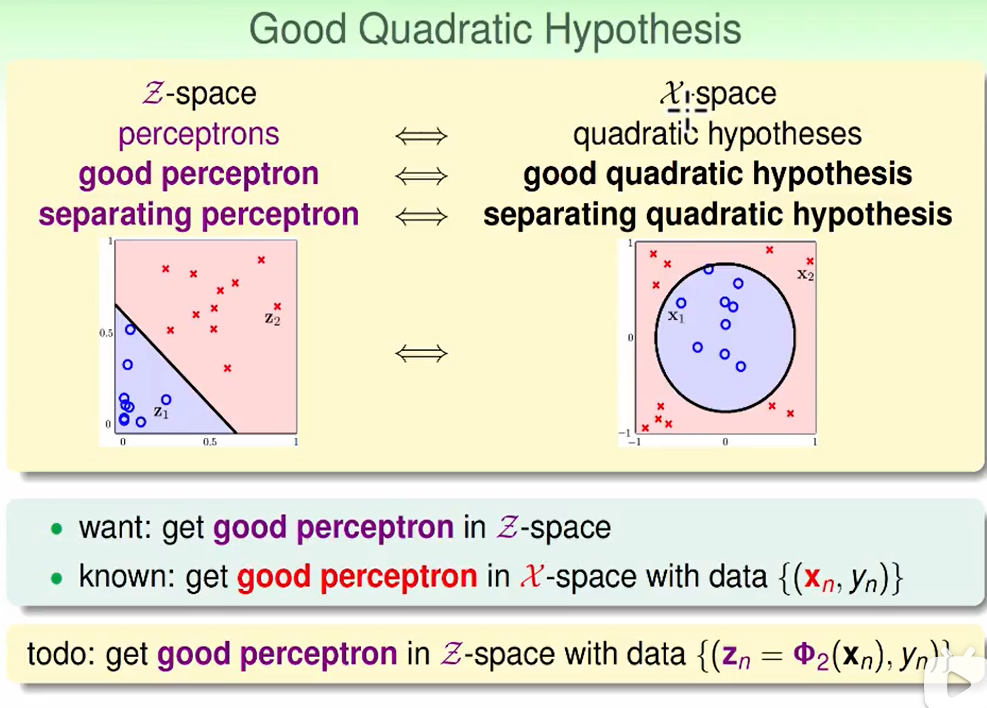
我们可以把$x_1$ 对应到右边的$x_1^2$,那么就想到于把以x为基地的左图转为以z为基底的右图。

惊喜的发现，我们又把问题转化到了线性的问题。

不同的w赋值可以代表不同的model，这是一个很好的系统性的总结。

那么什么样的x图像都可以用z表示吗？

当然不是，如果我们细心会发新$h(x)=sign(w_0+w_1x_1^2+w_2x_2^2)$ 没用关于x的一次项，也就是说这个圆形是不可以平移的。

因此只有一部分特殊可以利用这个系统：

我们想要扩展到任意图形：

那我们就加上一次项。

Nonlinear Transform

因此我们想这么做一个过程：

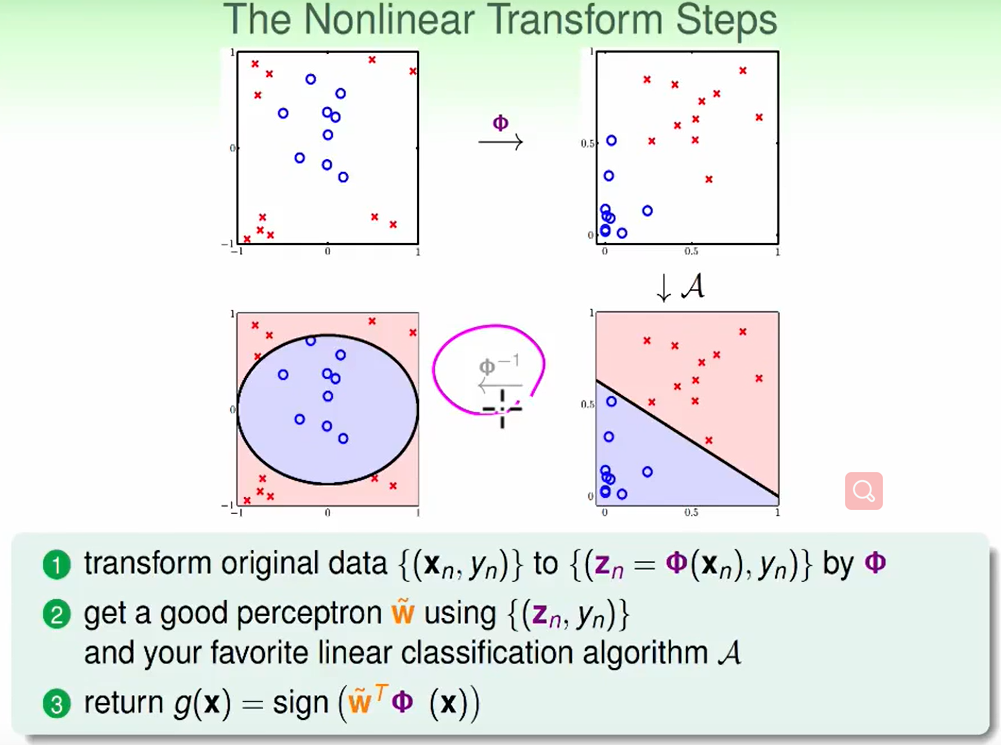
最后一个反运算$\phi ^{-1}$虽然不一定成立，但一般不会影响我们的结果，因为我们早早建立了每个点在新的以z为基地的坐标系下的映射坐标是什么，我们既然已经算出来了下图：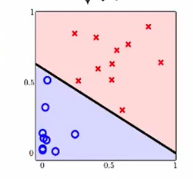

我们可以直接去找他对应的点是什么，无需做反变换。图中这么表示这是为了理解。

这个转化做完所有学的线性模型都可以用了。

但是这么做有没有什么代价呢？

Price of Nonlinear Transform

如果是一个Q次的多项式：

那么我们需要多少项来表示呢？

这个量级大概是$O（Q^d）$,即w大概要这么多项，这个w大概就是$d_{VC}$。

• 所以Q很大时，即用了一个高次的函数来划分类别，$d{VC}$就会很大，这样导致了$E{in}$和$E_{out}$差距就很大了，但是这种效果往往在训练的数据集上表现得很好。
• 反之，如果我们选一个很简单的低次函数来划分，$d{VC}$小一些，虽然$E{in}$和$E_{out}$比较接近了,当然这会使得我们的训练效果很差。

这是一个机器学习中很重要的trade-off(权衡)

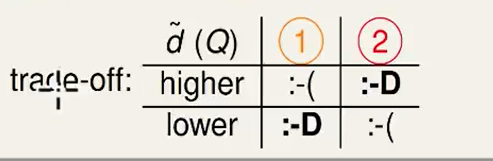
我们看上图可以发现，我们最后甚至提出了一个$d_{VC}=1$的方法，真是太好了。

但其实我们仔细想想，能提出这样一个想法，是因为你看到了这个数据图：

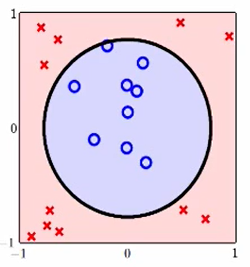
你看到长得像圆形，没有偏离原点，所以你说我们不需要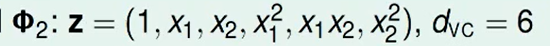

这种的变换。

那如果是一个超高维的数据，你分类就不可能看到数据情况了，你也想象不到高维体的样子，所以你只能老老实实的用$d_{VC}$大一些的方法。而我们直接提出的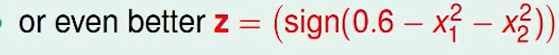

这种方式，是经过人human learning 学到的，不是machine leaning学到的。

Structed Hypothesis Sets

我们转换到新的坐标下，新坐标下的Hypothesis肯定是有包含关系的，如下图。

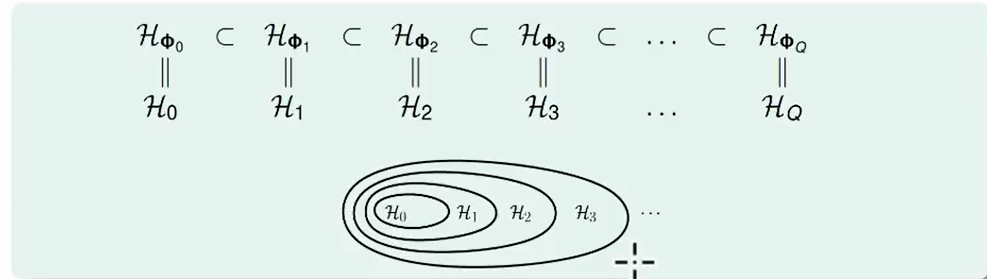
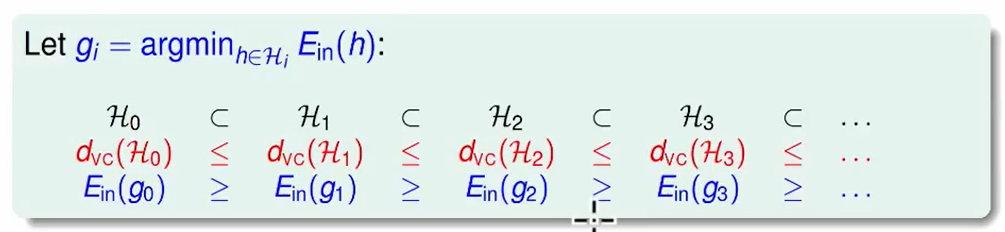
同理我们不难推理到$E_{in}$

从上图我们可以看出转换到一个很大的$d_{VC}$，并不是很好。

比较安全的做法是：从$H1$ 开始一个一个增加 ，直到$H_t$计算出的$E{in}(g_t)$足够好