CH13：Hazard of Overfitting

What is overfitting

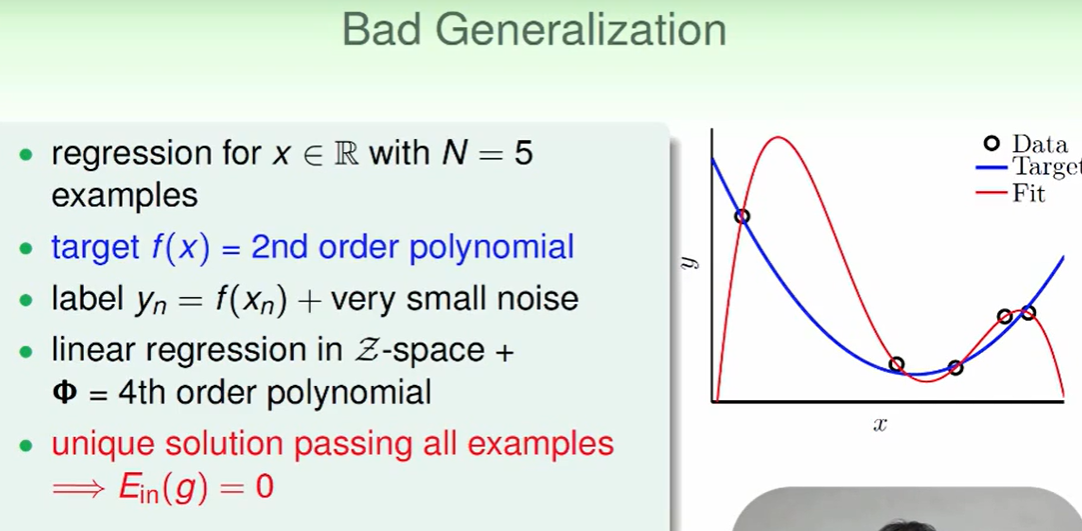
比如我们现在的数据是通过一个二次曲线+noise 造出来的数据，然后我们用这个数据进行机器学习，假如你用了5次曲线（即一定可以经过上述的五个点），那么我们就会画出图中红色的曲线(且$E_{in}=0$)

但是她和我们的target function蓝色线差距很大。

一个overfitting的例子：

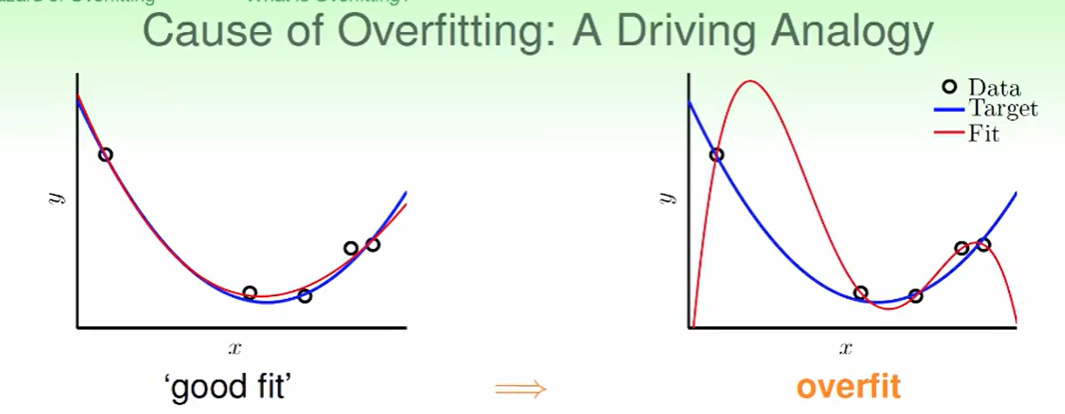
overfitting出现的原因：

我们以出车祸为例子。

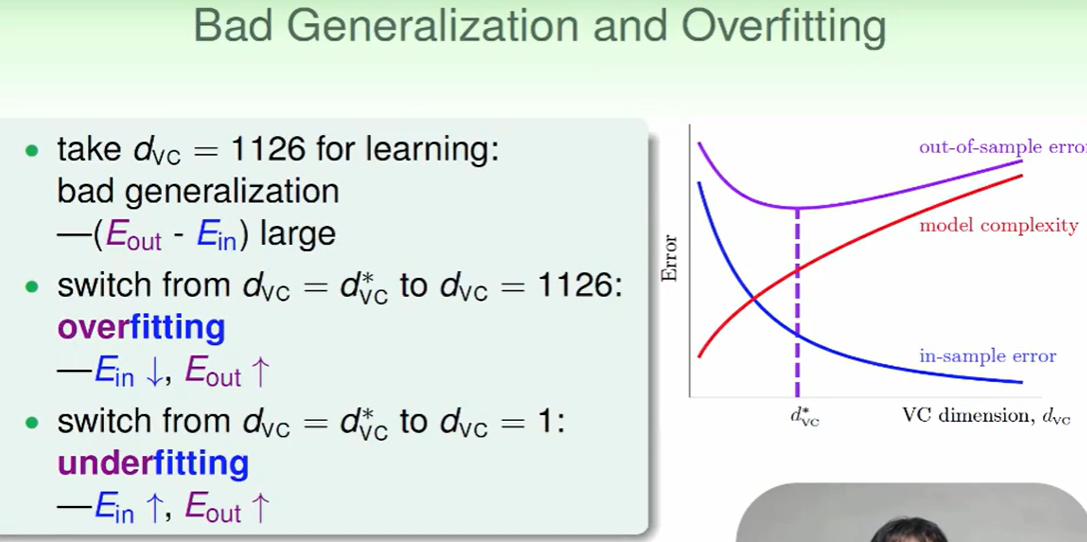
• 用的$d_{VC}$太大，开的太快
• 噪声，路不平
• 资料少，路况不清楚

The Role of Noise and Data Size

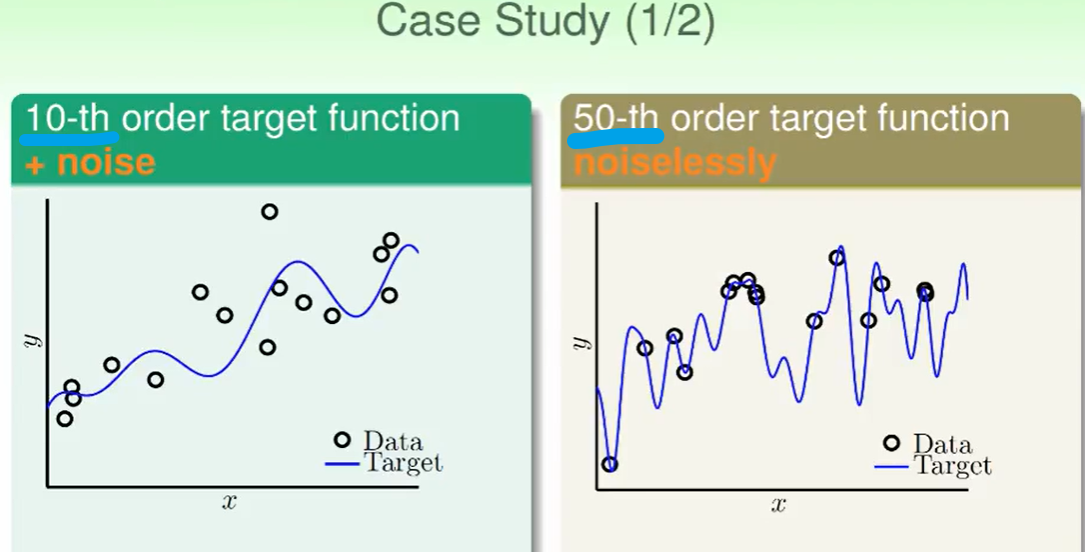
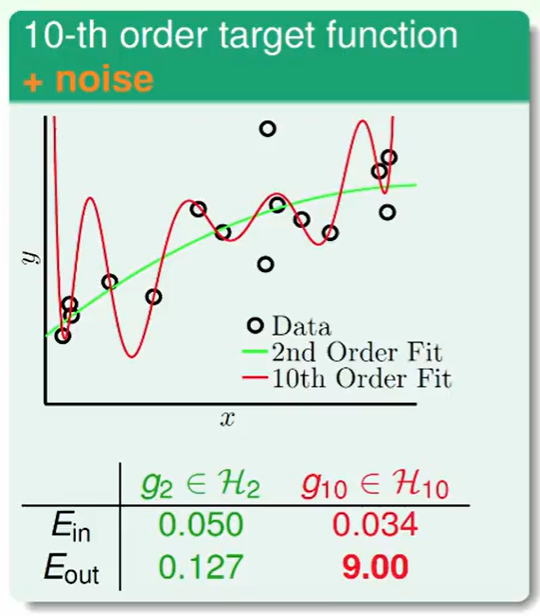
我们发现10次多项式还是发生了over fitting，在$E_{out}$表现很差。

我们会经常发现，有时候即使如果target function是10次的，我们用十次模型的效果竟然没有二次模型表现好，这是为什么呢？

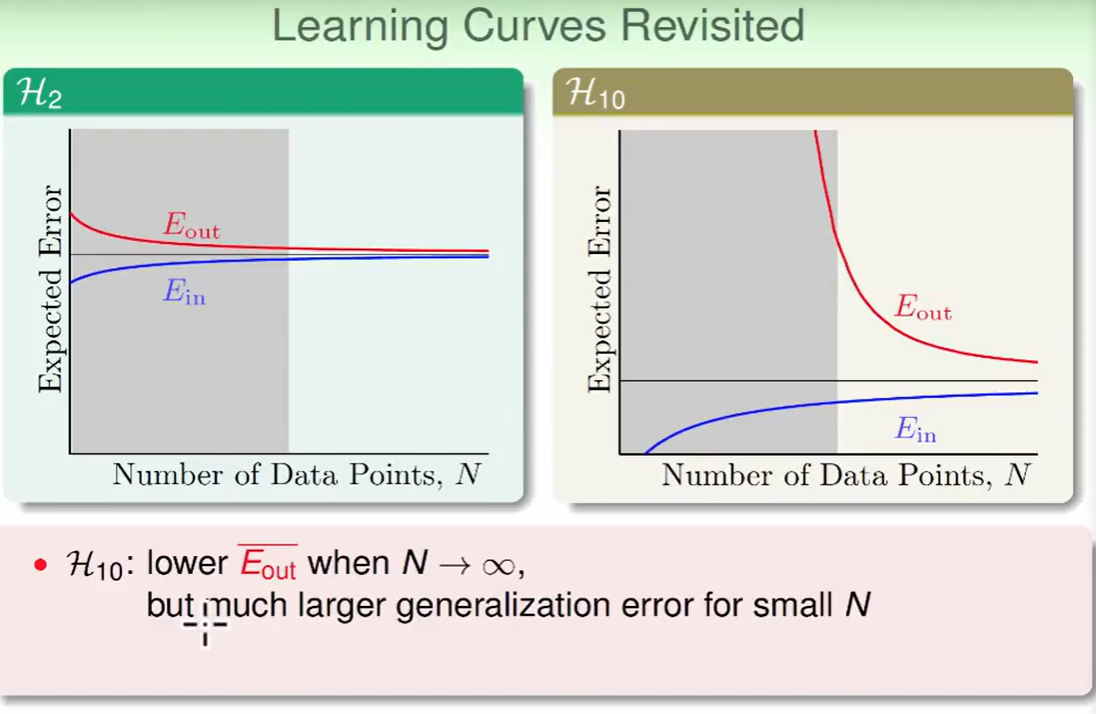
我们看右面的图，会发现在灰色部分 $E_{out}$表现非常差 ，这是一种聪明反被聪明误的特点，因为hypothesis太多了，在数据较少时很难寻出来一个好的模型。

Deterministic Noise

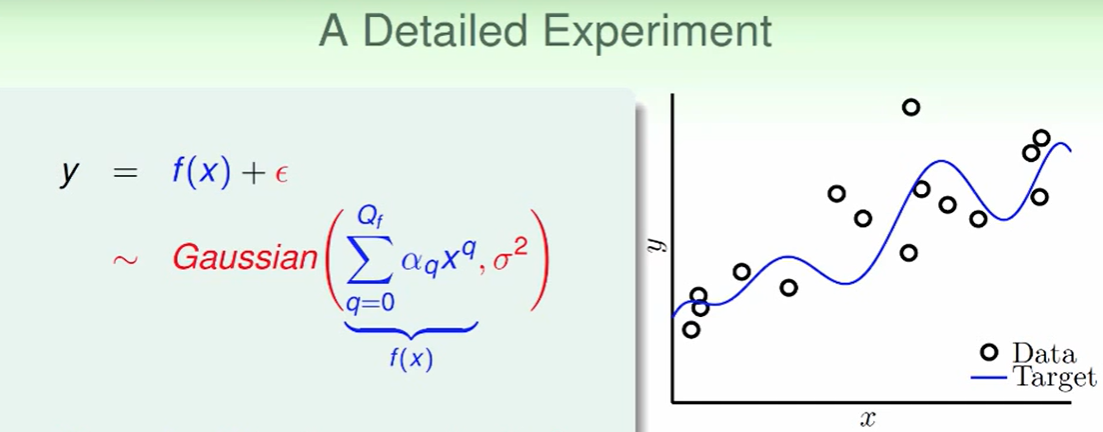
我们给出的数据y由两部分合成：target function+noise。这里noise符合高斯分布来看。

我们想研究影响overfit的因素，首先要确定overfit的measure方法

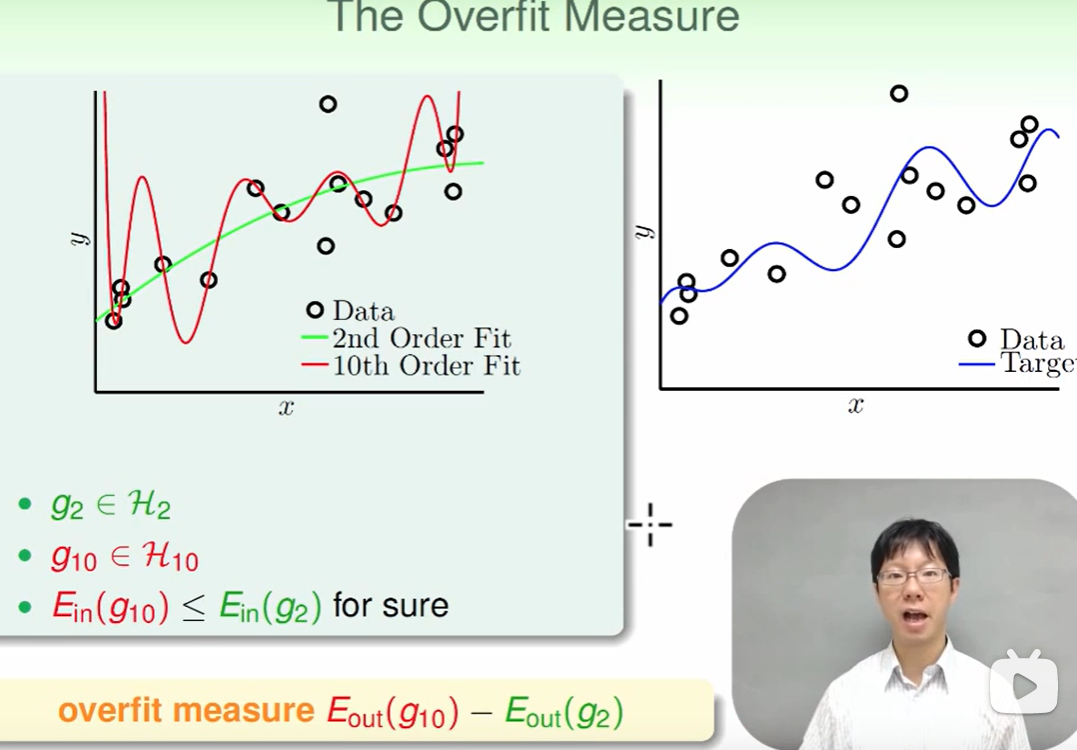
这里我们想到，如果overfit的越厉害，那么反映在$E_{out}$上来看就是差距很大：

下面我们来看不同不同影响因素造成的overift情况：

注：$Q_f$代表用的target function是几次的函数。

我们先看noise 和 数据量带来的影响

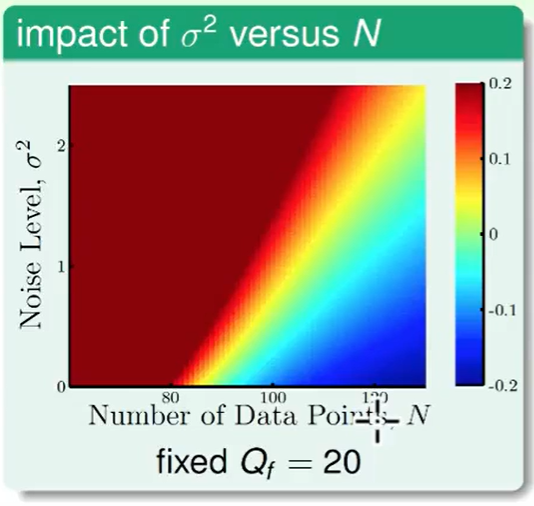
• 左上方深红色，不难理解，noise很多数据很少，差距肯定比较大，表现不好
• 蓝色部分数据多，noise少，肯定表现得不错。

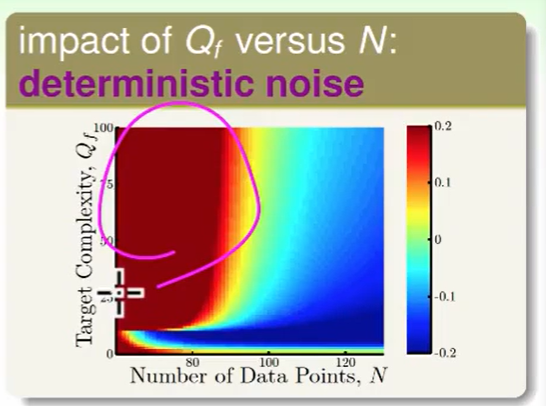
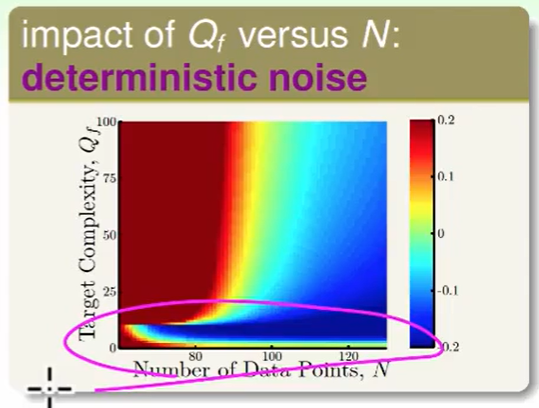
我们看一下 target function的次数($Q_f$) 和 数据量带来的影响

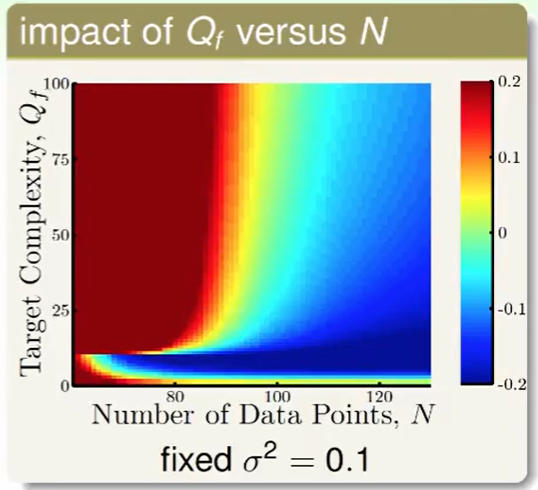
• 深红色，我们的目标函数非常复杂时，且数据数量又少肯定我们做不好。

从上面两个图，我们总结一下overfit的情况：

• 数据太少，

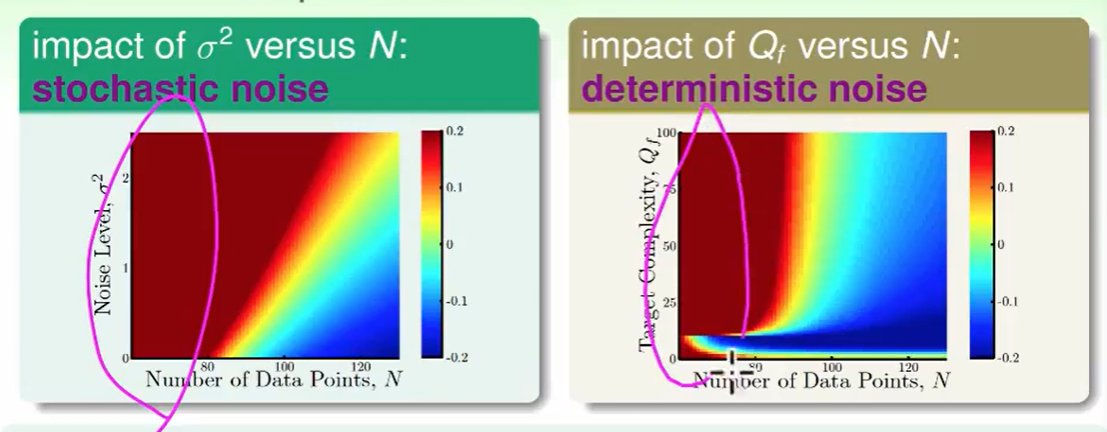
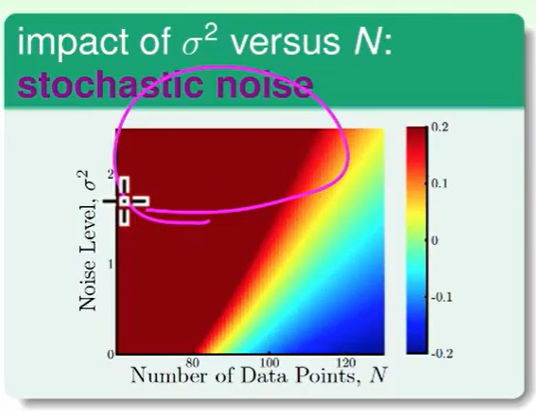
• stochastic noise太多，

• deterministic noise 太多

  

• excessive power造成的overfit，因为target function的复杂度很小时，我们用一个10次的多项式去拟合，因为他的能力太强了，肯定会把noise也拟合出来，这样就造成overfit

  

---

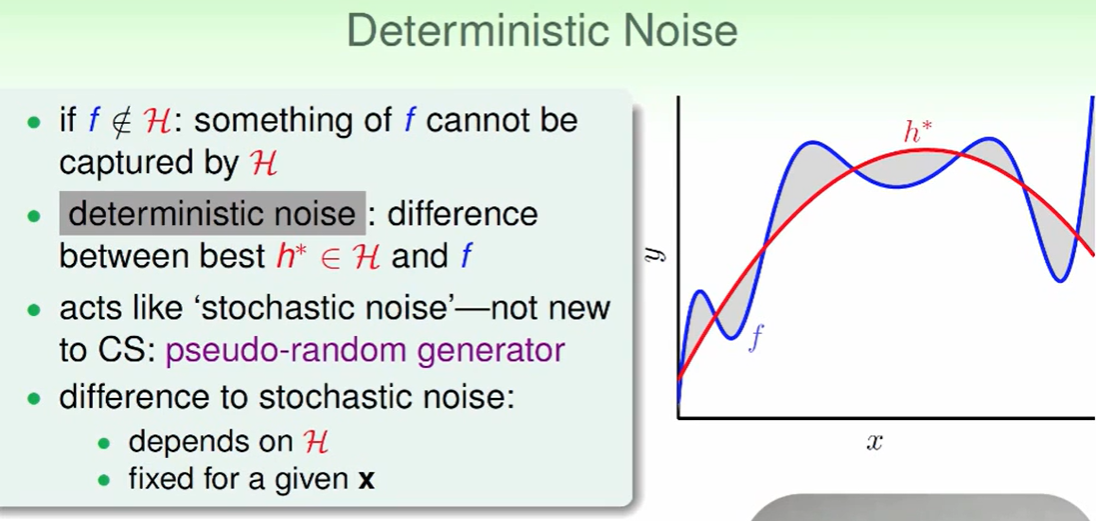
• 当我们的hypothesis(红线)的复杂度小于target function(蓝线)时，他们之间肯定会有差距，即灰色的部分，我们一般称这个差距就是deterministic noise
• 其实所有的 stochastic noise都是电脑伪随机出来的，其实本质上也是deterministic noise。

Dealing with Overfitting

我们之前讨论了产生overfit的原因，我们反向思维即可，得出解决的方法：

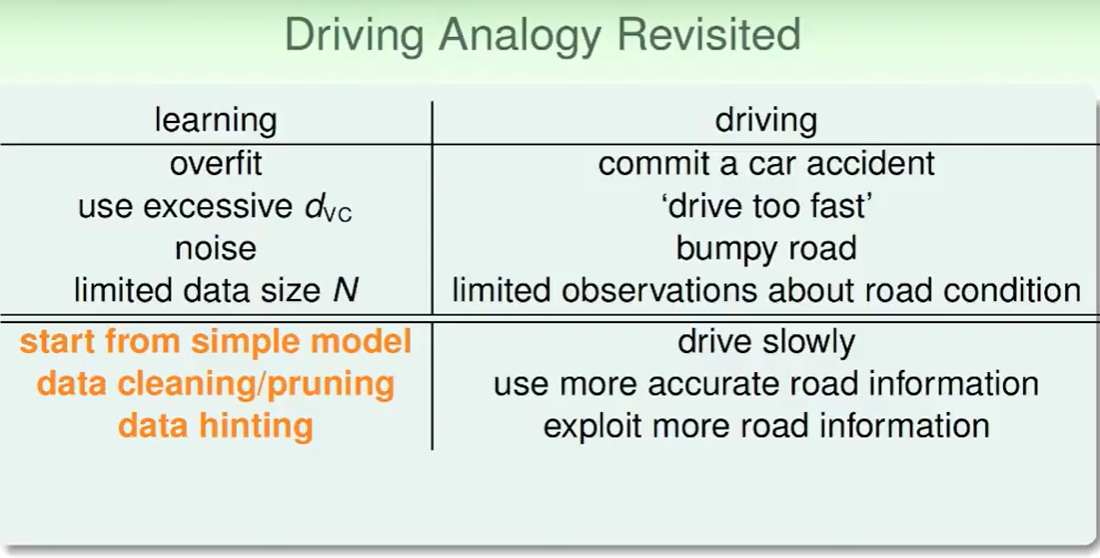
• 简单的模型
• 数据清洗/去除
• 多一点数据

除此之外，我们还可以用以下方法：

• regularization（下一节说）
• validation（下一节说）

---

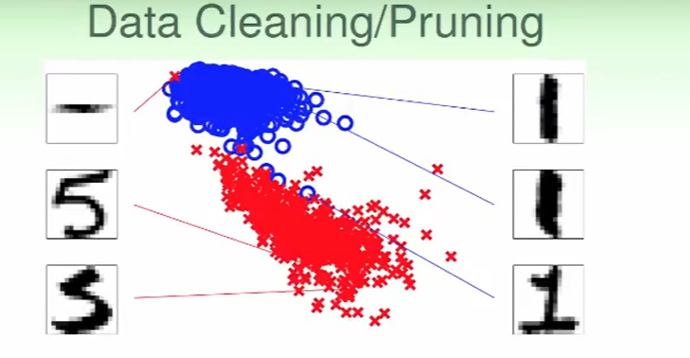
比如左上方的，这个居然认作5，这肯定是错误的，因此我们想要去掉这种离谱的错误。

可以这样解决：

• 如果监测到了5，但是他很接近1（身边都是被认作1的点），或者说这个点距离其他5的数据点太远，那么我们大概就可以认为这个数据可能是错误的。

• 我们直接改成他的label即可，我们称这样的操作为data cleaning

• 或者我们直接扔掉这个example，我们称这样的操作为data pruning

---

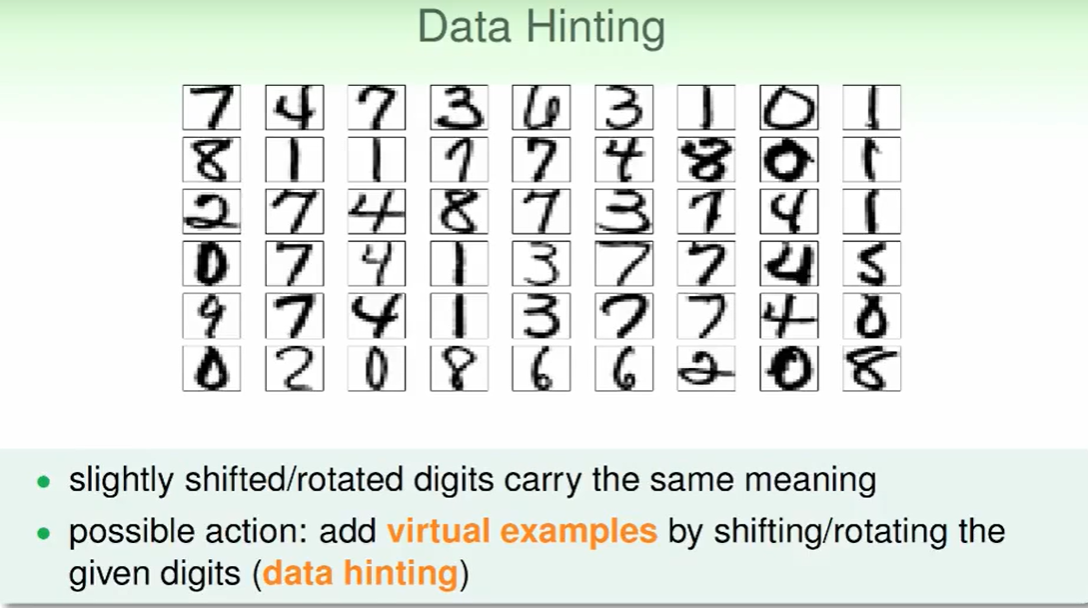
如果我们手上的数据有限，我们又想多一些资料，可以这么做：

• 对原来的资料进行轻微的旋转/平移操作，但不改变资料的实际意义
• 添加到数据集中，我们称之为data hinting（数据微调）