第三章 行列式

3.1 行列式介绍

注: $det \ A$ 代表行列式A的值

一个矩阵展开成代数余子式可以按行或者列展开（即 定理1）

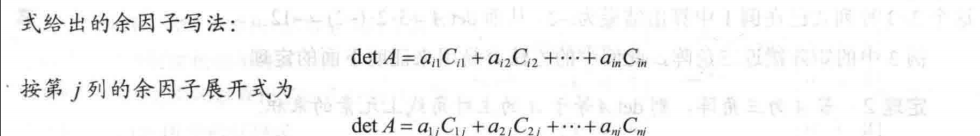
定理2：

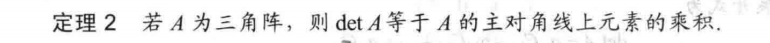
3.2 行列式的性质

行变换的性质：

可逆与行列式的联系：

列变换：

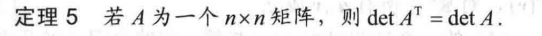
有了定理5我们不难想到，行列变换规则是一样的。

行列式乘积：

例题：

行列式函数的一个有趣的线性性质：

证明：(2)这个其实就是列变换，显而易见

​ (3)我们可以按照$x$所在的列进行展开，就很好证了。

3.3 克拉默法则，体积和线性变换

克拉默法则：

证明：

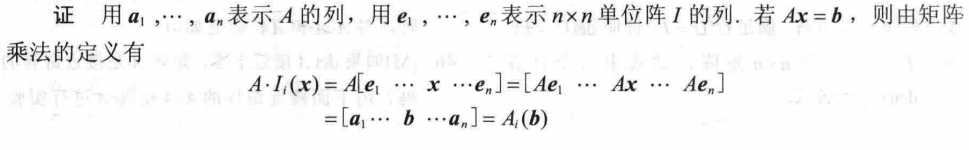
例题：

逆矩阵公式：

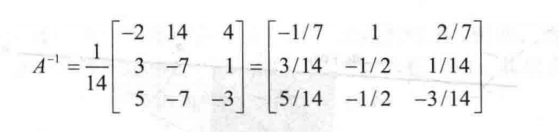
行列式表示面积/体积：

矩形很好证明这个问题，但是如果是平行四边形，我们化成对角矩阵计科。

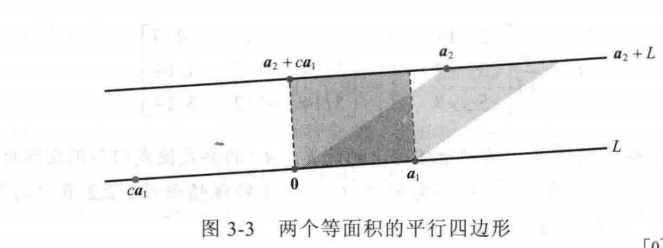
这个结合图也可以直观的理解，这是不会改变面积的。

如果是3*3的矩阵：

这个也不难理解，我们可以通过行列变换把平行六面体变成正方体。

线性变换：