CH14：Regularization

Regularized Hypothesis Set

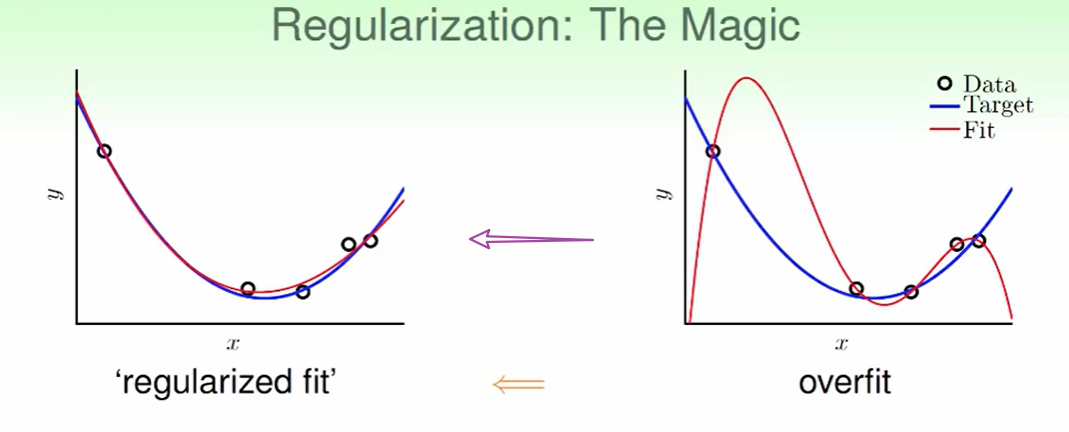
我们之前由于overfit造成了右边图所示的状况，我们今天要把右图转化为左图通过：Regularization

因此我们要从高次的hypothesis走回到低次的hypothesis，因此我们想找一种方法可以提供一种指标使得高次走回到低次。

---

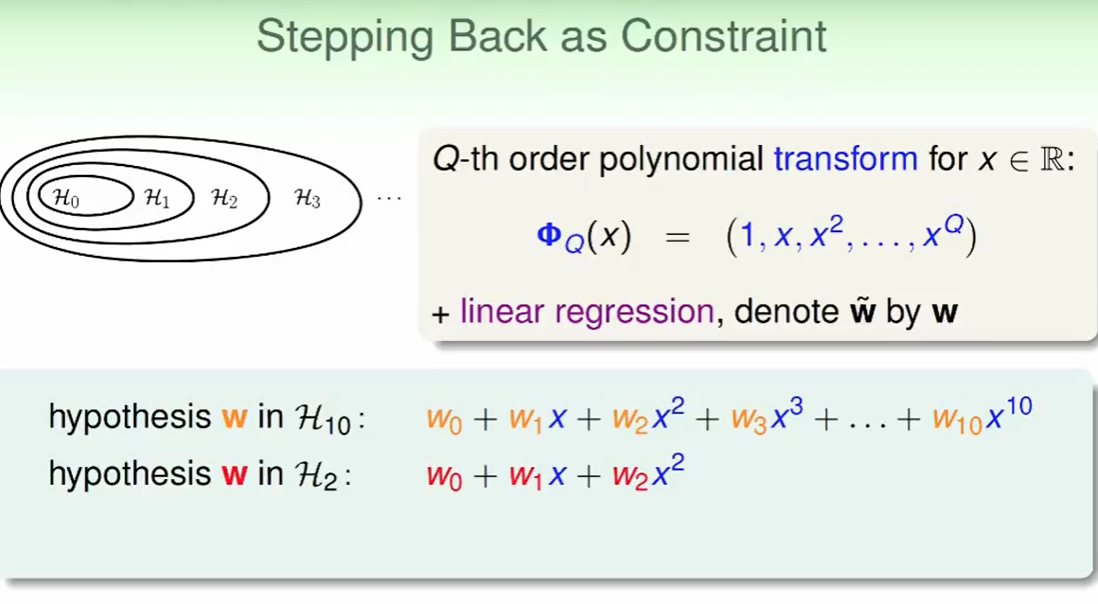
因此我们可以看出：低次多项式其实就是高次多项式 加上了一些限制

比如上图的限制就是：

因此我们上文所说的让高次走回到低次就是通过这个constraint来做到的。

那为什么不直接用3维呢？

其实我们的这个constraint是可以looser一些的：

比如我们可以不控制具体哪儿个$w$是0，而是限制$w=0$的数量

那么我们此时得到这个新的hypothesis $H_2’$ 的特点是：

• 比$H_2$ 要更宽松一些
• 比$H_{10}$要严格一些

但可惜：这个$H_2’$ 的解是一个NP-hard 问题

我们可以找一个和这个类似的looser的constraint，比如：

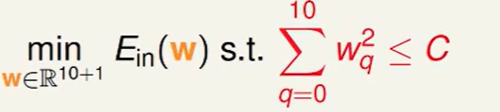
我们对每个w的和进行限制。

我们称这样的hypothesis为$H(C)$:

观察不难发现，通过调节$H(C)$ 它可以在H(0) 到$H_{10}$之间，太好了这样不就让他自己去寻找适合的复杂度了吗！

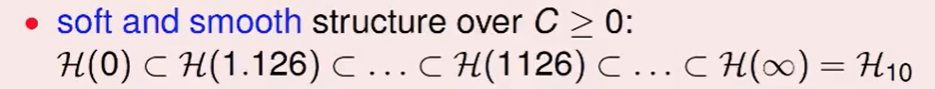
我们称H(C): regularized hypothesis set

Weight Decay Regularization

我们把$H(C)$写成矩阵形式：

即：

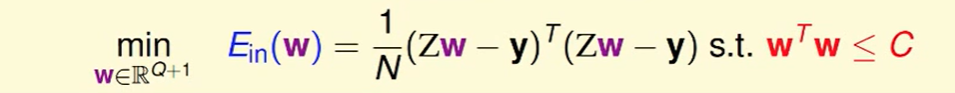
我们还是考虑用梯度下降法来做这个问题：

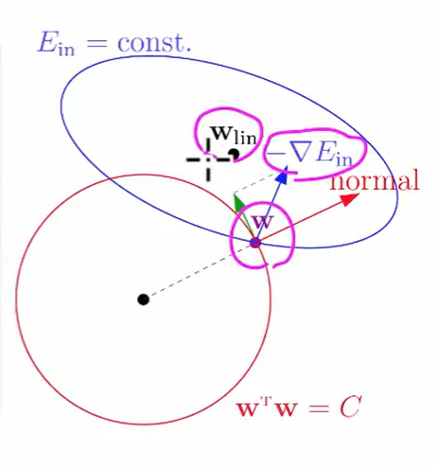
​ 梯度下降会滚到我们做linear regressions的划分处，但是我们还有一个条件：

$w^Tw\le C$ .

​ 我们可以这么想如果你要进行梯度下降，你的方向不能沿着normal(上图红色的线)防线，要你沿着圆的切线下降，即绿色的箭头。

也就是说直到w向量与梯度反方向平行时，我们没有w向量的法向量方向的分量了，此时就不用在更新了。用数学表达这个问题就是：

我们此时要解决 这个问题：

我们把梯度算出来带进去直接（线性回归那节的内容）：

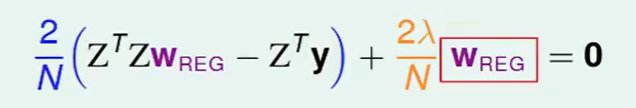
我们消掉无关的N，2,得到：

称为ridge regression岭回归

我们理解一下这个问题：

原来我们在做linear regression的时候：

我们做到梯度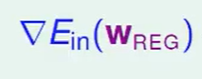等于0时，说明了$E_{in}$此时最小。

我们类比一下，我们现在做的这个就相当于：

我们要解$w$, 不妨用上图中下面的式子来做：

因此只要给我$\lambda$ ，我们就可以解了。

我们来看一下不同$\lambda$对结果的影响。

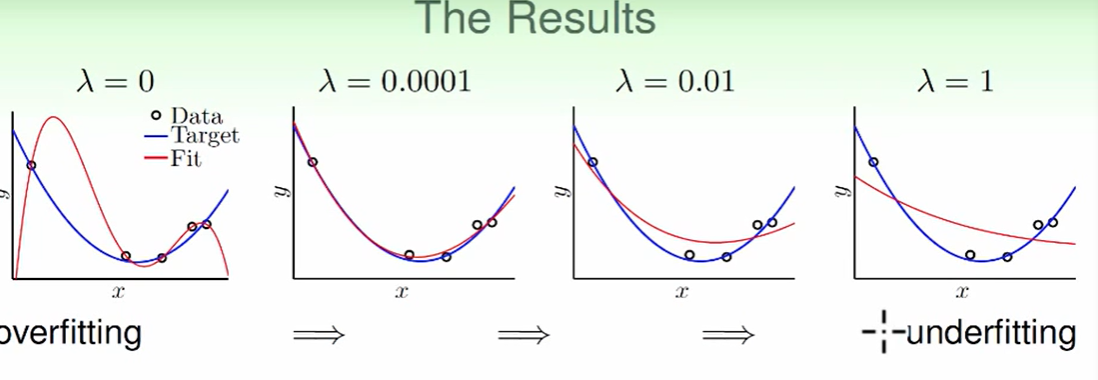
我们发现$\lambda$ 很小的时候就可以做到很好的结果。

因此说明我们加上一点点的regularization就可以让效果变得很好。

$\lambda$ 越大，向量w越短，C越小。

这个东西像是在惩罚。

（Legendre Polynomials）勒让德多项式：

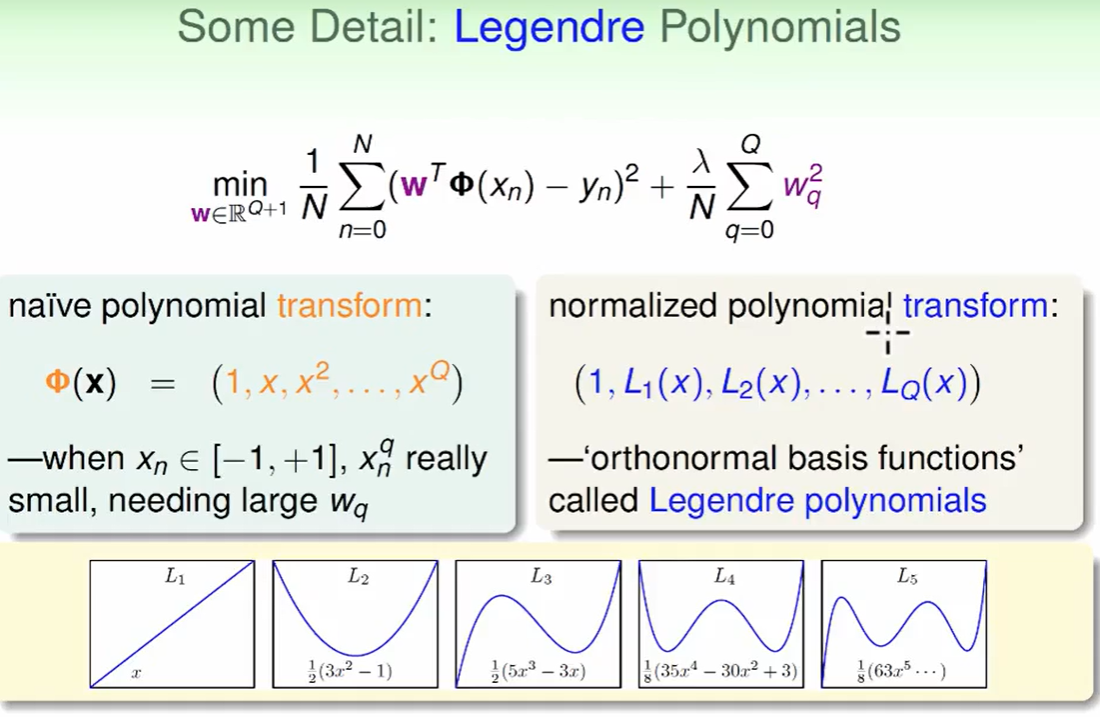
我们让不同方向的x做一下规格化正交，成为规格化正交的方程（orthonormal basic functions），也叫（Legendre Polynomials）勒让德多项式。这样效果会好一些。

Regularization and VC Theory

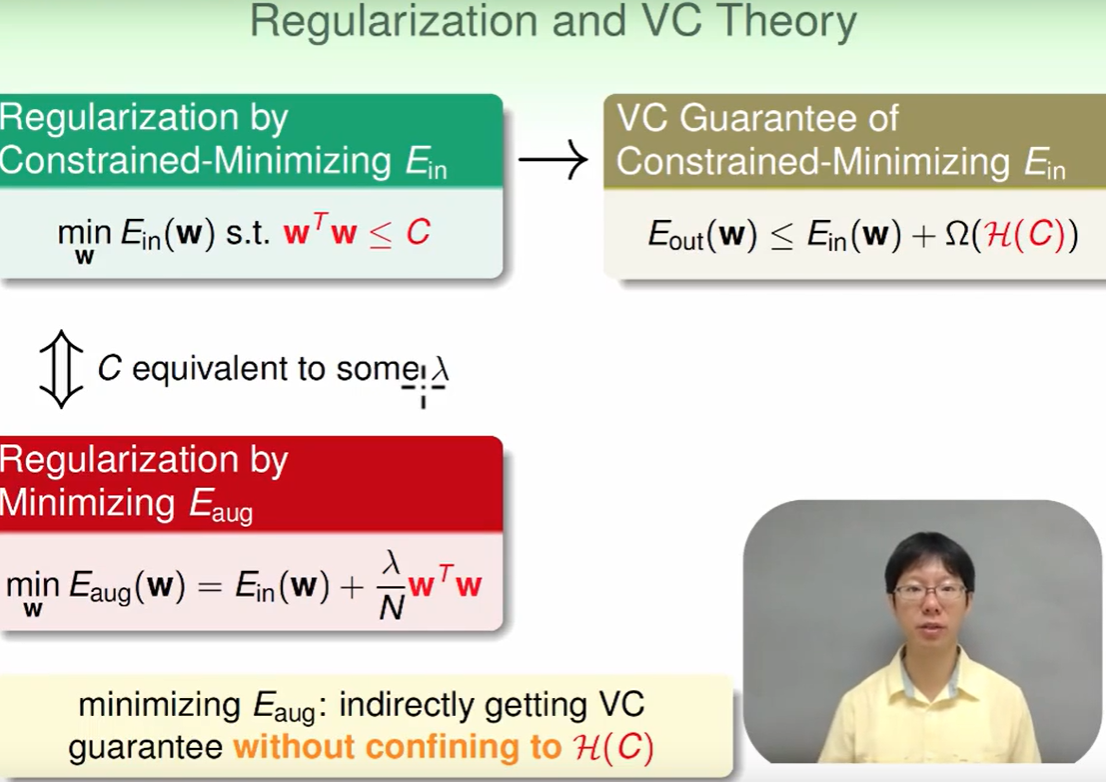
• 我们把问题转化为了问题：，这个C通过$\lambda$来表现。

• 我们的VC保证是：

我们仔细观察发现 这个Augmented Error 和 VC Bound长得有点像：

• 我们的代表的是具体的一个hypothesis多么多么的复杂，比如多项式次数很高

• VC bound中的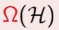代表的是hypothesis set有多么多么复杂。

• 因此我们发现，如果一个hypothesis非常复杂，那么他所属于的hypothesis set也不会很简单。

  因此这是一个很好的替代品。

我们通过regularized（正则化）后，$d{VC}$ 会变小的，我们称为：$d{EFE}$。

即：Effective VC Dimension，这个$d{EFE}$ 会小很多相比于原来$d{VC}(H)$

General Regularizers

我们一般加上怎么样的正则项(Regularizers)呢？

比如我们今天训练一个模型，我们认为最后的target function是一个类似于偶函数的function。那么我们训练一个多项式的时候，偶数幂次项系数不用管，奇数幂次项系数尽可能小，才能使最后训练出来的函数类似于偶函数，那么此时的正则项就是：

比如我们想要选出比较平滑/简单的hypothesis，就加上这样的正则项：

比如我们想让最优化时比较方便那么我们就加上这样的正则项：

---

L2正则：

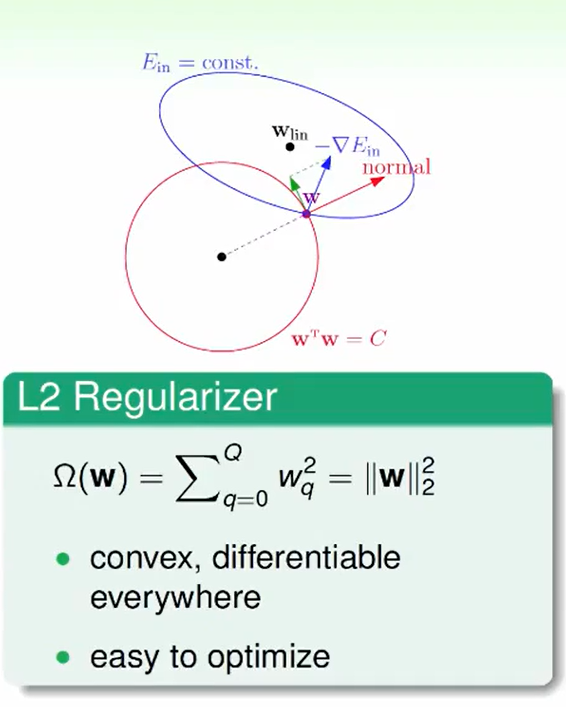
处处可微分，所以容易找最优解。

L1正则：

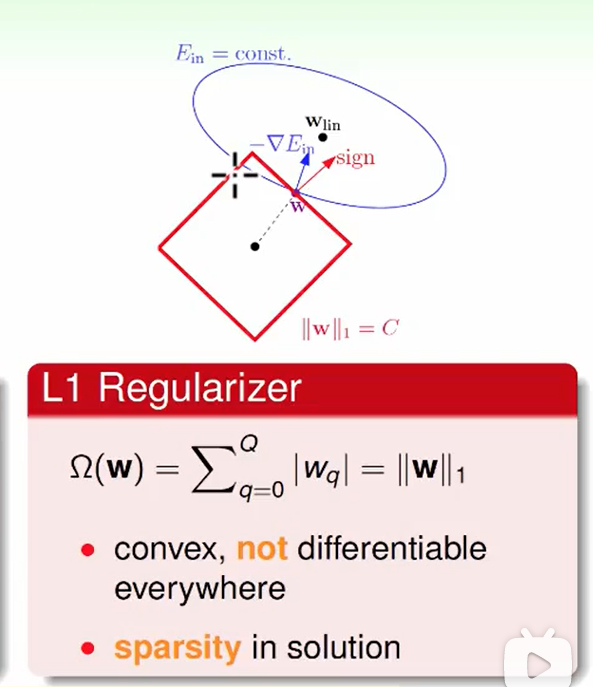
• 他不是处处可导的

• 解很稀疏，这是因为由于梯度下降，会沿着正方形边缘来走，直到正方形的角，才有最优解。我们再来思考一下这个方形的角有什么特点呢？特点就是它会使大部分w项=0，少部分w项非0，因此他求的是一个稀疏的解。

• 举一个生动的例子：我们训练了一个1000多维的模型，但是我们不想让解这么麻烦，怎么办呢? 我们只需要做一个L1正则化，让解稀疏一些，比如1000项的w可能900多项都会变成0，那么我们计算的速度就加快了很多。

---

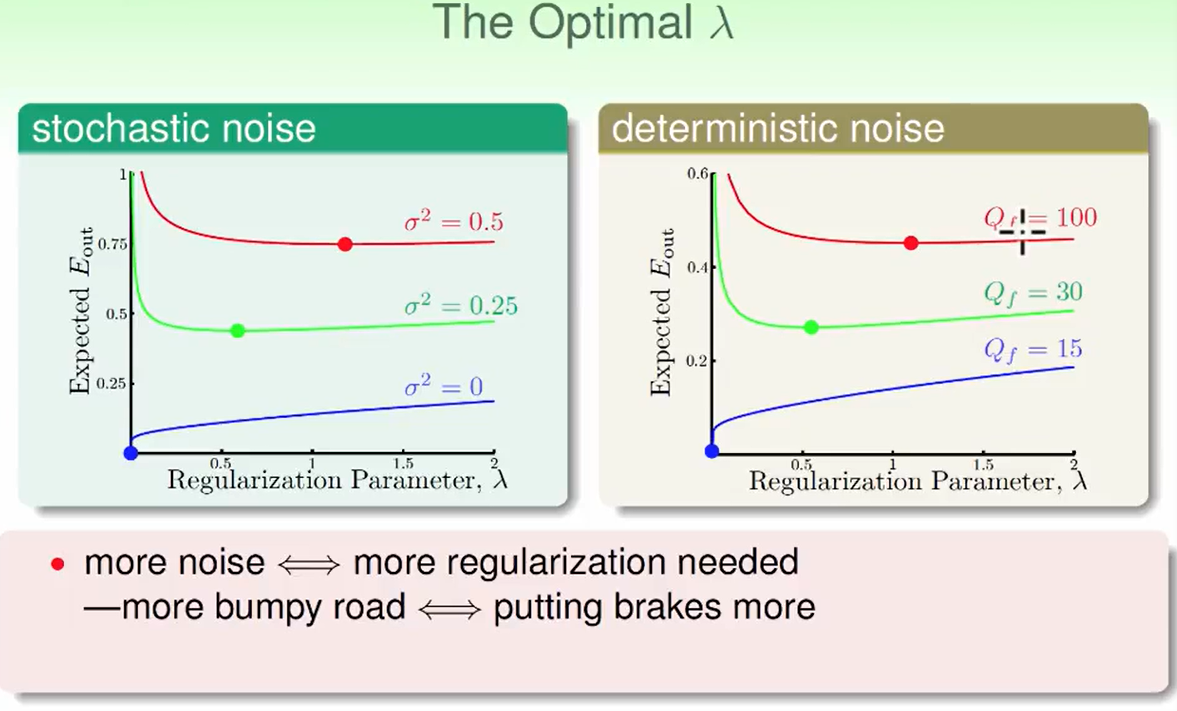
我们结合上面两个图发现：噪声越大，$\lambda$越大，这个不难理解，路越陡峭，就要多踩刹车。

但是我们一般是不知道噪声是多大的？所以我们也没法选择正确的$\lambda$，这也是下一节要解决的问题。