CH15：Validation

Model Select Problem

选择的依据：

• 第一种：只做$E_{in}$ 做低一些，这样选模型肯定不是很好

• 第二种：选择在最终测试集上的一部分数据，然后对每个模型进行测试，然后选取准确率最高的。

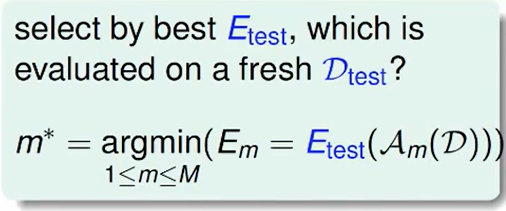
  由hoeffding不等式来看，这样的结果还不错：

  但是现实中我们几乎不能拿到最终测试集的，这是一个自欺欺人的做法。

以上两种方法都不是很好，或许我们可以折中一下：

​ 我们留一部分资料，但是这一部分的资料不用于训练。然后我们用其他资料训练，然后训练完的模型再测试刚刚的资料。

​

Validation

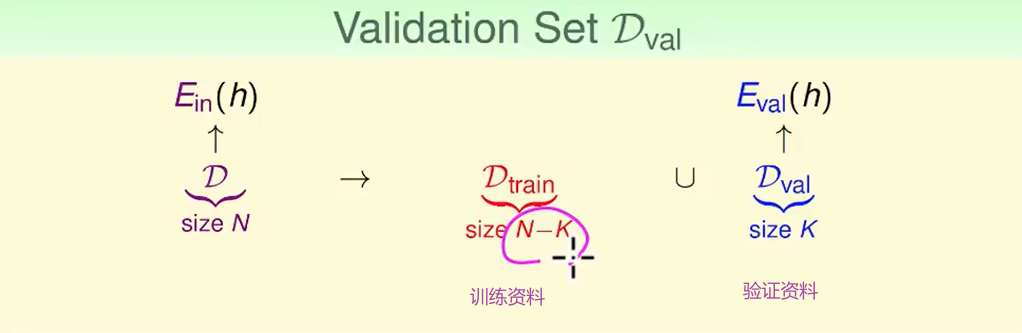
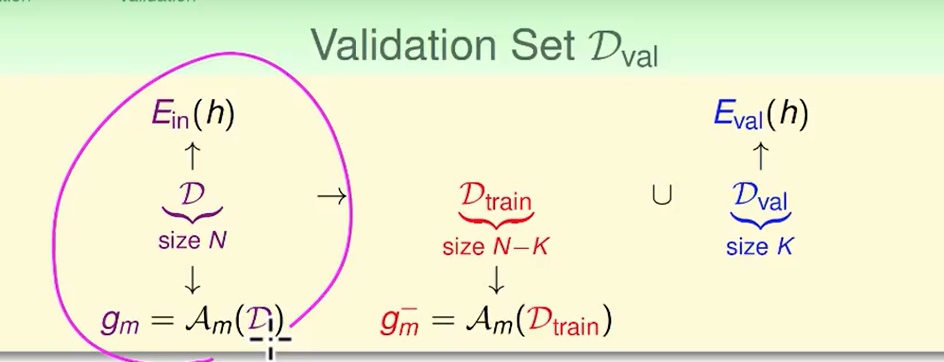
从霍夫定不等式不难得出这样的保证：

​ 我们选择错误率最小的即可，但是选择完后，比如第27个hypothesis的错误率最低，这个模型最好。那么我们直接27个hypothesis直接输出就OK了。

​ 但也许我们可以做的更好一些，反正已经知道这个模型做的最好了，为什么不训练的时候直接把测试集也扔进去训练呢？我们的learning curse告诉我们，当模型确定，资料越多准确率越高，反正我们已经确定了模型，那不如把模型重新用所有数据训练一次。

​ 数学语言来表示就是：

这是我们validation的过程：

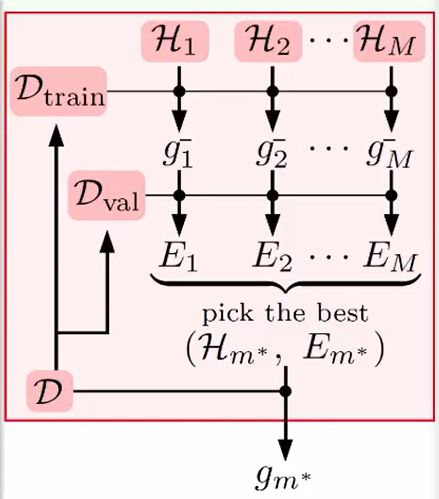
我们观察不等式：

其实就是两次的约等于：

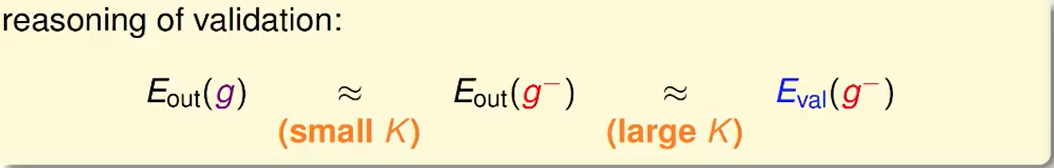
但是左边是想要一个小的K的，而右边想要一个大的K。

这就成为了一个有些矛盾的地方，经验之谈，一般K取数据量的五分之一：

Leave-One-Out Cross Validation

今天我们考虑一种比较极端的情形：

K非常小，$K=1$：

$D_{val}^{(n)}$: 代表除去第n个资料的资料集。

$E{val}^{(n)}(g_n^-):$ 代表用$D{val}^{(n)}$训练出来的model做validation的时候的错误率是多少，这个错误率由于只有一个测试数据，那么这个值要么是0要么是1。

$E_{val}^{(n)}(g_n^-)$ 要么是0要么是1，这样肯定是无法反映一个model的好坏的。那么如果我们有很多个$e_n$，即去掉不同的数据分别测试结果，就可以解决这个问题了。

我们希望得到：

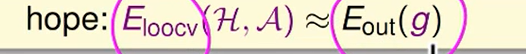
举一个简单的例子：

比如数据集一共三个数据，我们有两种model，分别是 线性模型和常数模型：

不难看出常数模型效果更好。

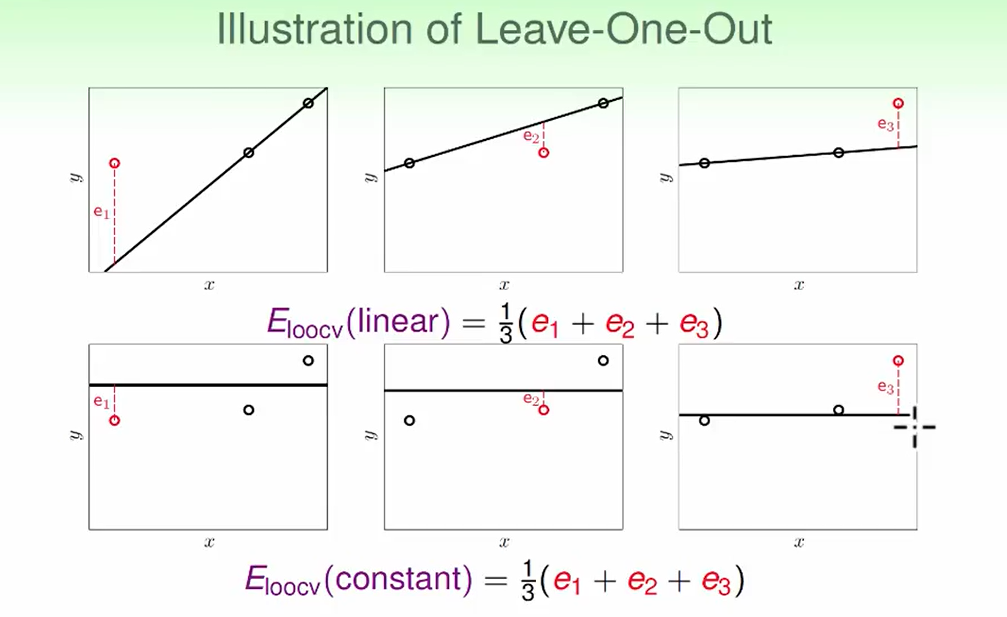
我们想要说明一些$E{loocv}(H,A)$和$E{out}$的关系：

我们可以发现cross validation所作出来的错误率和$E_{out}$很相近。

V-Fold Cross Validation

​ 上次提到的Leave-One-Out cross validation的方法复杂度有些高。每次都要送进去算一次，但是如果是线性回归的话，每次做都是有闭式解的还比较快一些。因此线性回归比较适合Leave-One-Out cross validation，但是有些模型我们是没有办法很快算出来的。

​

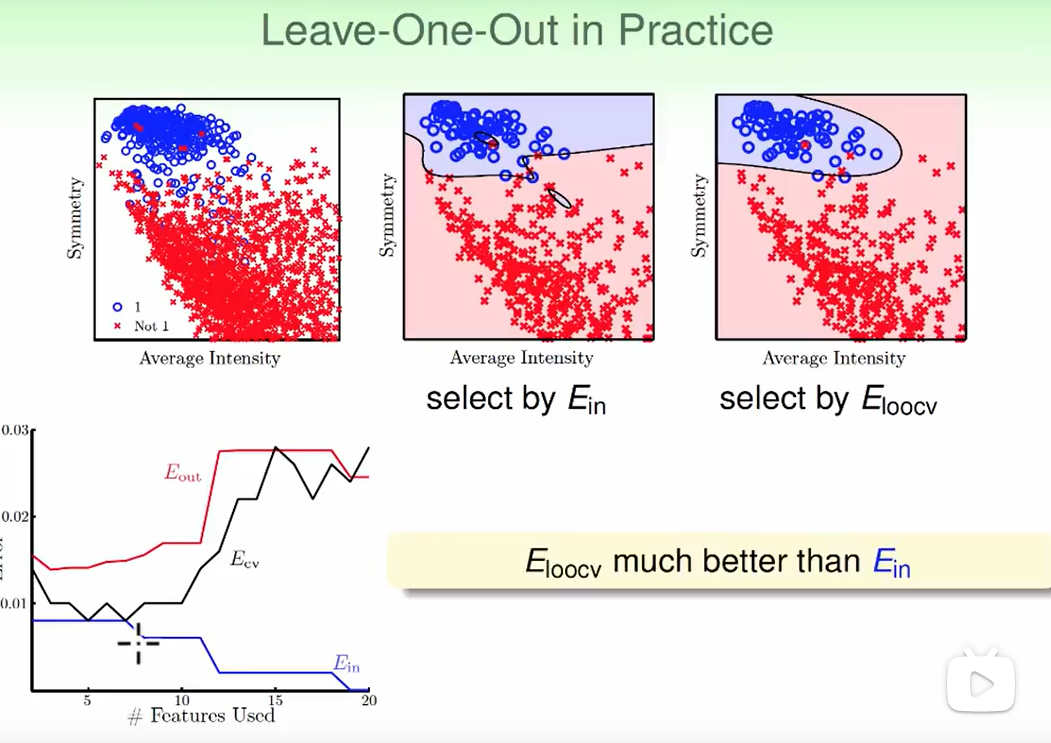
Leave-One-Out cross validation还有一个缺点就是他的跳动比较大，因为每个的取值不是0就是1，这样就造成了得出来的错误率不太平滑，也不够稳定，如下图黑线上下跳动：

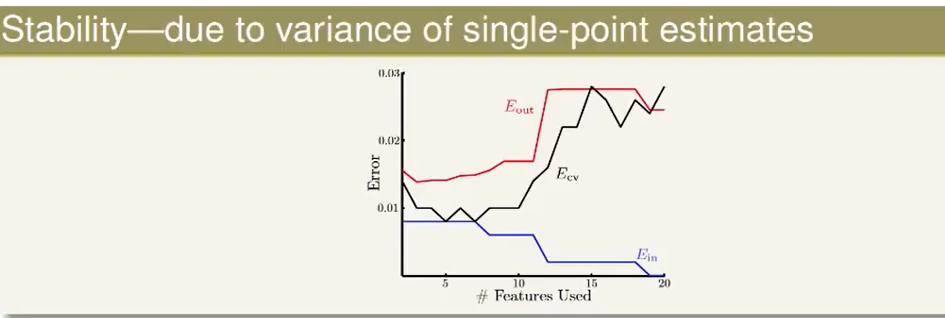
所以Leave-One-Out cross validation并不是很常用，只有某些特定情况下才会使用。

---

那么怎么减少计算量呢？

比如1000个数据，我们不再切1000份去做Leave-One-Out cross validation，而是选择等量的分成10个部分。

然后用每份去做平均，而不是单单的一个一个的去做平均。这样一定程度会加速计算，减少计算量。

我们一般分成10份：

• 我们先是选择一个好的model在所有的hypothesis

• 然后用cross validation的去训练我们的模型，并选出一个调成最好的参数。

• 然后去用这个训练好的模型测试真正的结果$E_{out}$效果如何

我们要记住 我们选择去做validation只是因为他可以保证我们的模型做出来效果不会太差，但是模型真正的好与坏 只依据$ E_{out}$