CH1：Linear SVM

Large-Margin separating Hyperplane

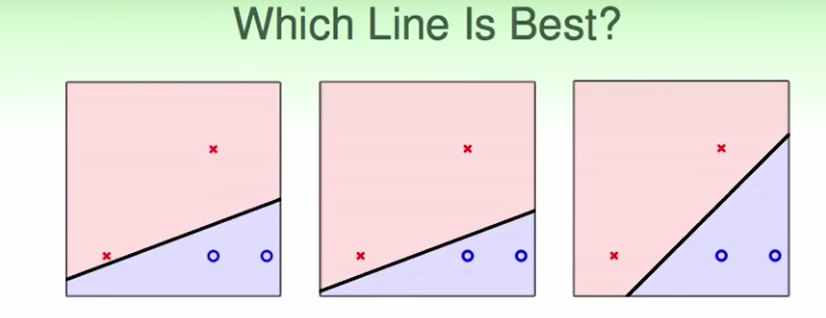
这三种线都可以把这些点分开。

• PLA算法不一定会得出哪儿一种线

• 

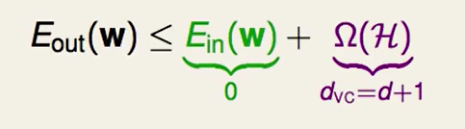
  从我们的VC Bound来看，$E{in}=0$都一样，$d{VC}$=也一样，那么 VC Bound所带来的保证$E_{out}$都相同。

​ 但其实我们的直觉告诉我们第三种好一点，因为他如果有一些数据有误差，那么也不会影响结果，因此我们一般认为第三条线对错误容忍度高一些。

---

​ 简单理解就是如果点距离分割面/分割线越远，那么他容忍noise的力度越大，我们在基石课中学到，noise是造成overfittng的原因，容忍noise能力越强则更不容易带来overfitting。

---

因此我们想找健壮性更强一些的线，什么是健壮性更强的呢？就是点距离分割面/分割线越远。我们直观理解就是这条线可以有多胖。

如下图：

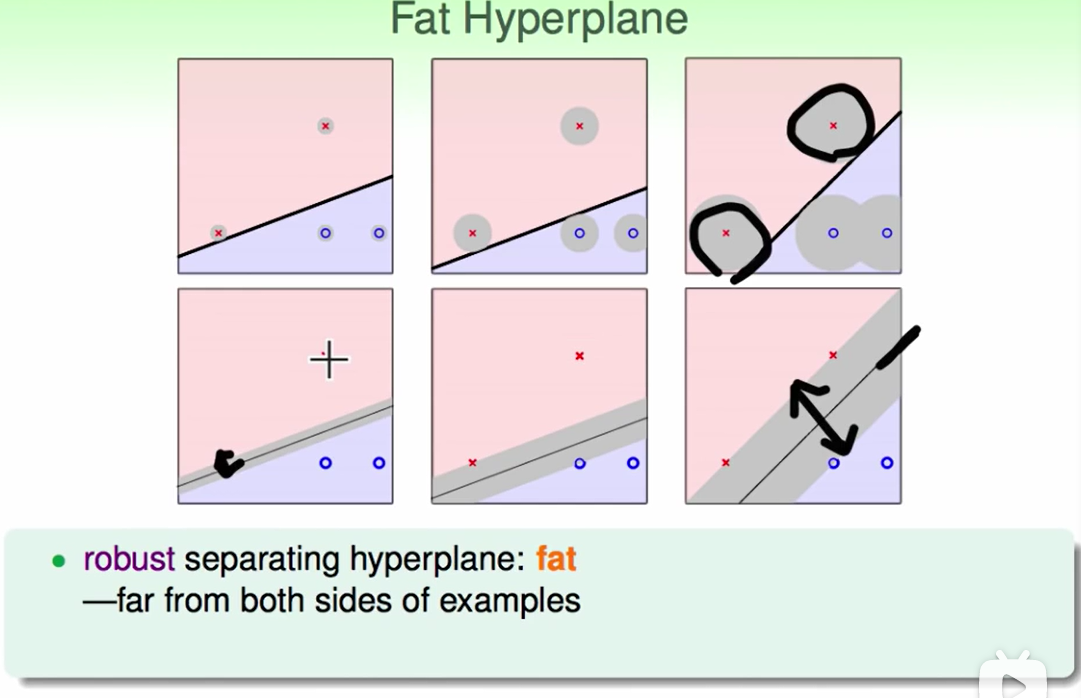
灰色就代表这条线有多胖，这条线越胖越说明我们的健壮性越强。

那么我们现在可以给健壮性一个定义：

健壮性就是点距离分割线/分割面 最近的距离。

---

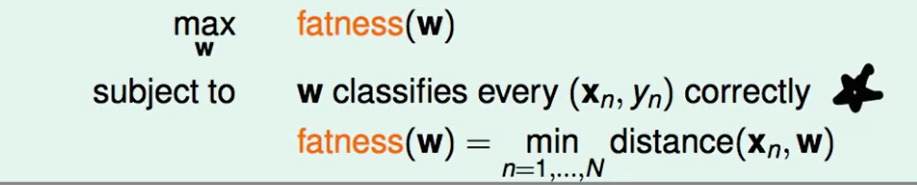
那么现在我们要做的就是最大化fatness(w)。

但是这个”胖“的说法似乎不太专业，这里我们给出真正的名字margin

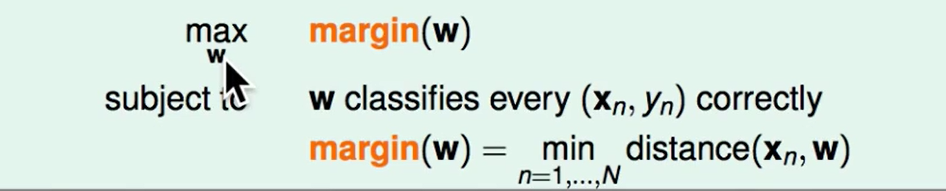
因此我们想要做到下面两点：

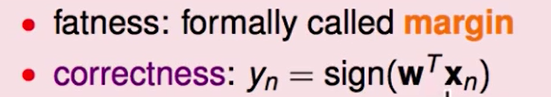
• Margin越大越好
• 分类正确

Standard Large-Margin Problem

我们要解决的问题是：

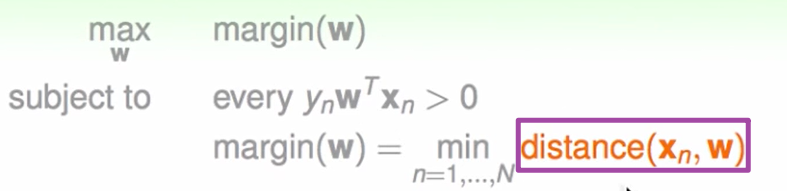
我们首先要知道距离怎么算。

我们之前算的时候是需要在数据第一列加上一列1的，然后用$sign(w^Tx)$计算分类结果，但是这里我们不在加上第一列1了，把w的第一列拆出来，那么判断就变成了：

---

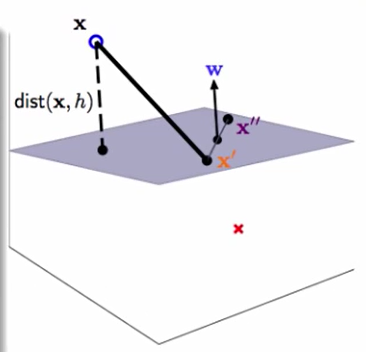
这个图上的$x’$和$x’’$一定是符合 $w^Tx + b = 0$ 的

因此:

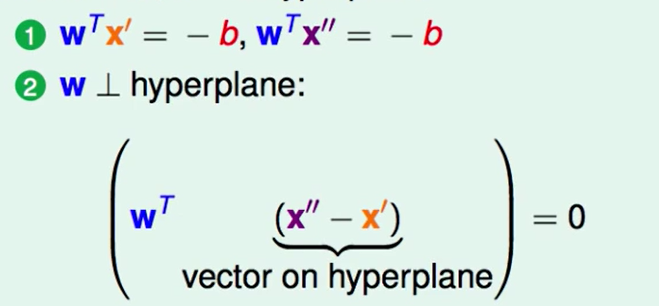
我们的这个权重向量一点是是分割面的法向量的。

我们接下来算距离：

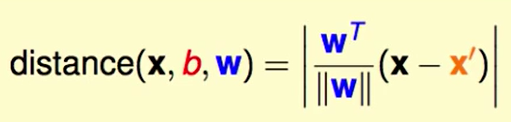
首先$(x-x’)$代表着这个蓝色向量，然后让他做投影，投影到w的方向。

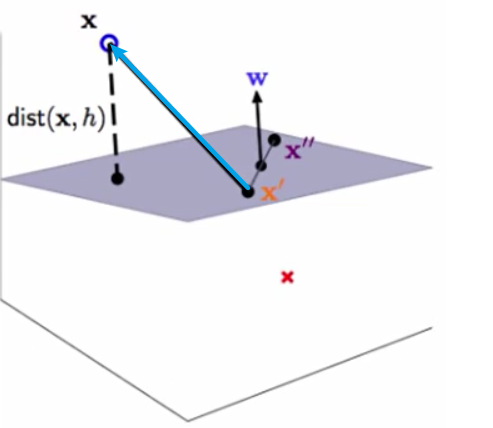
投影后的距离就是距离分割面的距离：

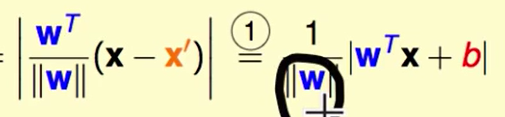
对于可分的平面来说：

因此我们可以脱去绝对值：

那么现在我们的问题转化为了：

---

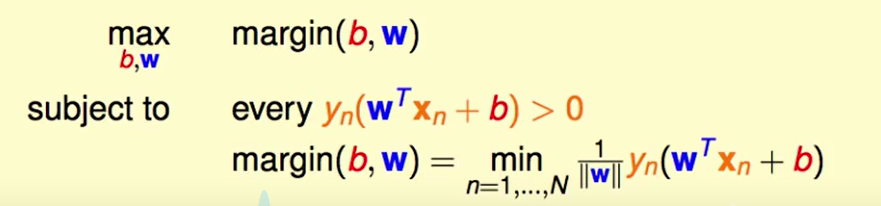
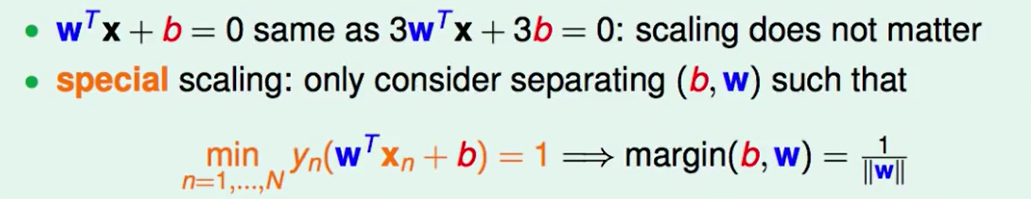
一条线是可以有多种表达方式的，我们这里只要保持$\frac{w^T}{||w||}$不变即可，因此我们放缩$w^T$,使其符合下面这个式子。

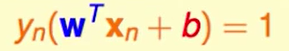
那么此时我们的距离就变成了$\frac{1}{||w||}$。

问题转化为了：

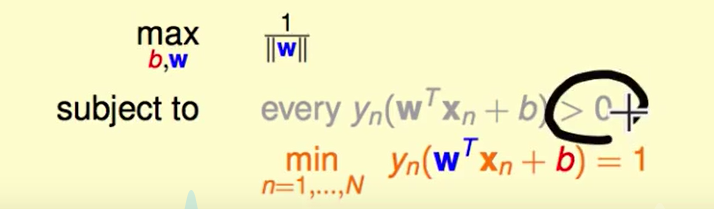
我们这里发现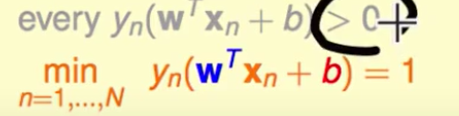

下面这个条件包含上面的条件了，因此只需要下面的条件即可。

现在问题转化为：

---

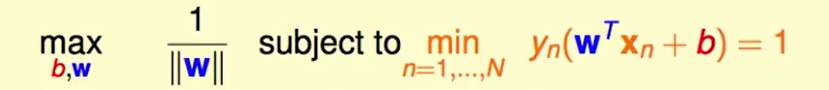
到现在位置问题中的min还是很难搞，我们如果可以放宽一些他的条件，但是结果还在当前条件的限制之下，那么我们的问题就好解决了。

我们用蓝色的条件代替紫色的，但这样很可能会导致

$y_n(w^T+b)$全部都大于1，导致最小的也不等于1了，那么这样放大了条件是没有什么意义的。

我们考虑假如真的全部都大于1，比如都大于1.126.

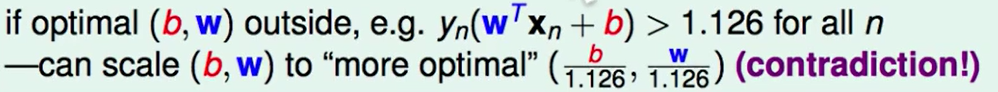
我们可以调整$w$和$b$的大小使得其重新满足条件，那么这个条件放大一些是不影响结果的。

那么此时问题转化为了：

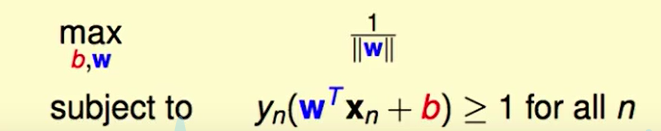
做一些小的数学变换，（这个$\frac{1}{2}$就是为了后面方便计算的常数，最大化最小化问题中常数不影响最优的结果）

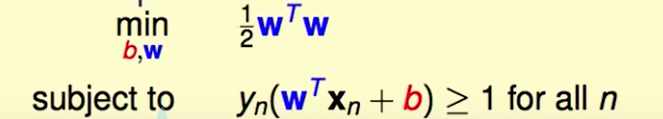
Support Vector Machine

我们以上图为例子：

我们不难得出下面两个式子

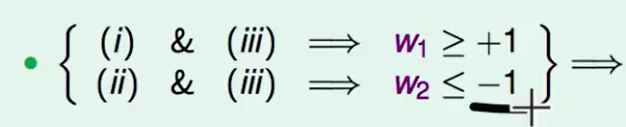
所以$w_1^2+w_2^2\ge2$,即：

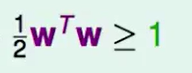
因此我们就可以算出这个最胖的线：

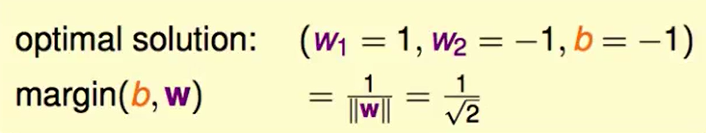
我们直观理解这个问题就是，我们通过支持向量(support vector)，也就是胖胖的线上边缘的那些点来算得这个胖胖的线。

---

但是上面是4个点，比较简单，那么如果包含多个点我们怎么做呢？

幸运的是，这是一种二次规划问题，我们有现成的工具可以解决，我们只需要把我们现在的公式转换为标准的二次规划问题表达形式即可。

我们只要找到左边的参数即可。

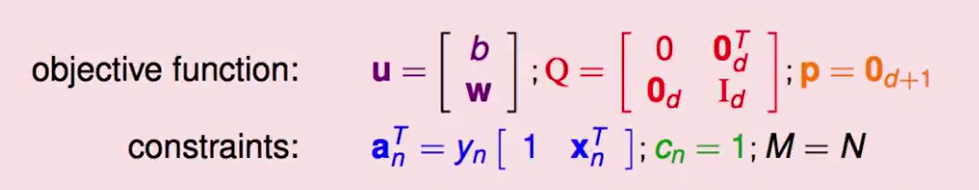
那么我们的Linear Hard-Margin SVM算法就搞定了：

怎么做非线性的呢？还记得基石里讲到的方法吗，做feature transform就好了。

Reasons behind Large-Margin Hyperplane

有趣的事情是，我们发现：

SVM怎么和regularization做的是相似的事情，都考虑了两个事情：

原来regularization做的事情可以防止overfit的原因体现在了SVM里。

---

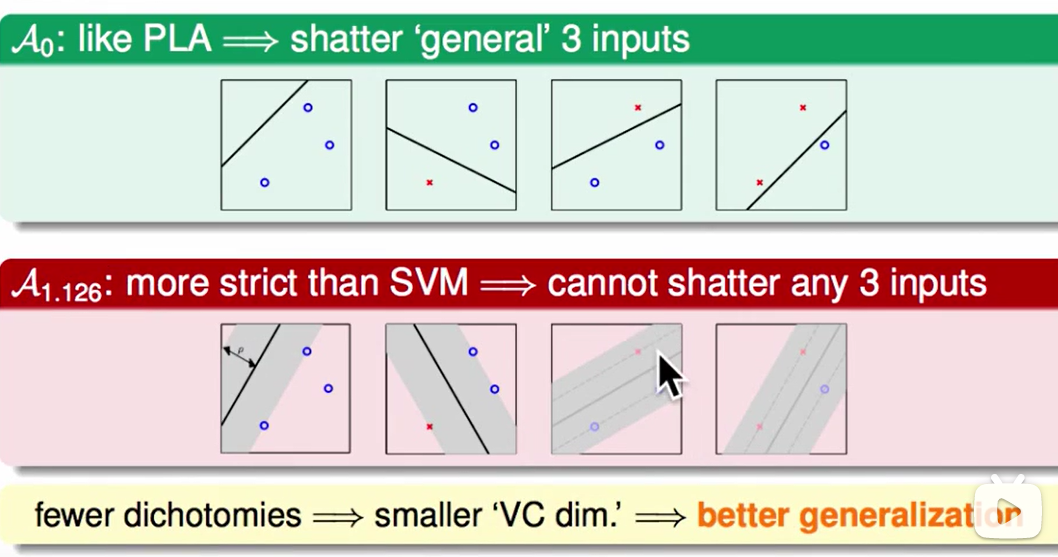
我们在之前的线性分类模型中hypothesis的数量可能很多，但是在SVM中比如我们要求这个分割面足够的胖，那么有一些在线性分类模型中的hypothesis在SVM中是不成立的(如上图)，因此VC Dimension会小一些，因此他的泛化能力更好一些。

对于上图三个点，如果不考虑胖瘦，那么$d{vc}=3$，但是如果要求宽度大于某个常数，那么$d{vc}<3$.

我们这里有一个现成的结果：

$\rho$代表SVM中的线的宽度，$R$代表半径，因此我们多了一种控制复杂度的方式。

---

我们有了large-margin hyperplane 我们可以同时做到 hypothesis set很小 并且 分界也更精细，即：