CH2：Dual Support Vector Machine

Motivation of Dual SVM

我们上节提到过，如果想让SVM来做非线性的分类，那么我们是需要feature transform的，此时的问题变为了：

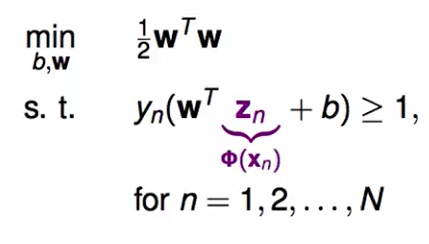
这个$\phi(x_n)$就是对原来的$x_n$做了feature transform。

我们的二次规划问题也变为了:

​ 为什么想到用SVM来做这件事情呢，因为在之前我们的linear regression中我们了解到，如果去做feature transform会导致$d_{vc}$变大的，也就是hypothesis set也会更大。而在SVM中，他有一个很好的性质就是由于分界面有厚度，导致一些hypothesis是不成立的，这就帮我们控制了模型的复杂度，我们就可以很好的使用feature transform了。

这里我们提出SVM的对偶问题：

我们这里把原来的$d+1$维转化为了一个只与N有关的维度。

提示：下面的内容许多包含最优化的问题，因此我们不会着重讲这些，而是当作现成的理论。

我们这里用到了一个工具叫做拉格朗日乘子（Largrange Multiplier）：

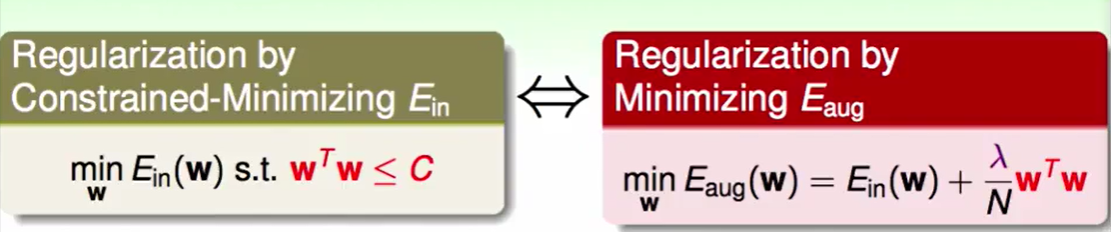
在之前的正则化问题中，我的的$\lambda$是给好的，但是在dual SVM问题中$\lambda$被我们看作给出的约束，并且我们需要去解$\lambda$。

在SVM中有N个constraint，那么也就是说有N个不同的$\lambda$。

我们把原问题转化为lagrange function:

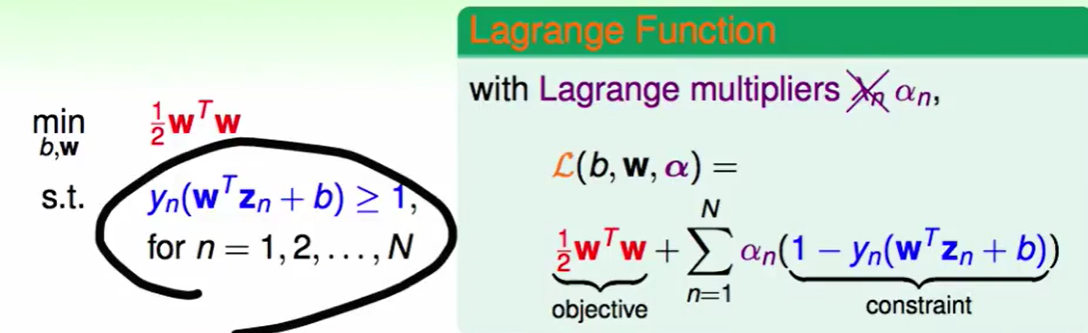
（要注意，学术文献一般喜欢用$\alpha$而不是$\lambda$，下面我们将替换掉$\lambda$）

我们直接给出SVM问题的数学表达：

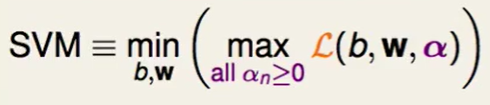
这个怎么理解呢？

我们拆开来看：

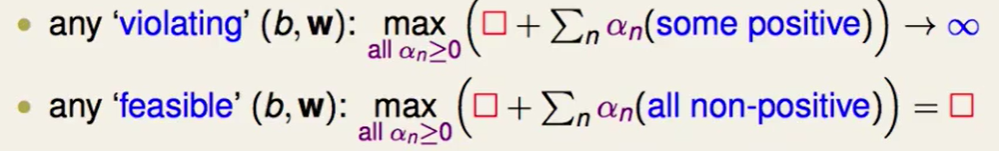
如果今天我们计算蓝色部分也就是这部分时，算出来是正数，也就代表$y_n(w^Tz_n+b)<1$,那么说明这是不符合我们constraint的，这是一个非法解。同时我们来看这样算出来的肯定会趋于正无穷的：

因为蓝色部分是正的，我们的$a_n$取无穷大就好喽，这样就达到max了。

反之同理，如果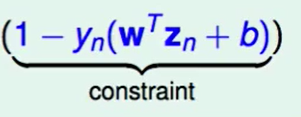这部分小于0，最后加算出来的值就是$\frac{1}{2}w^Tw$ , 也就说这部分是符合要求的解。我们再来看下SVM的表达式：

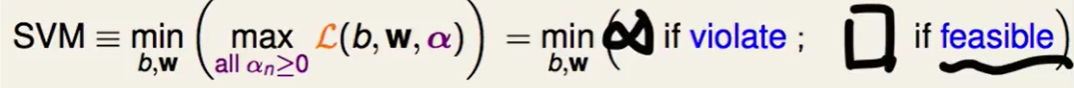
也就说这个式子帮我们选到了feasible的$b$和$w$。

Largange Dual SVM

上式是显然成立的。

上面式子告诉我们任何的$\alpha$取值都会小于左边部分，那么右边最大时也依然会小于左边的式子，即下图的式子：

我们称之为Largange dual problem（拉格朗日对偶问题），其实就是min，max换了一下顺序。

最优化的一些知识指出，如果我们可以做到：

那么我们就可以给下面的式子画上等号：

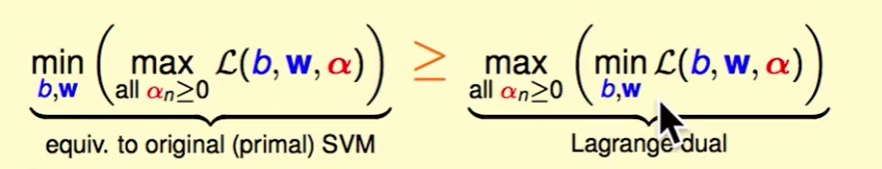
我们现在做右边的即可。

我们把$L(b,w,\alpha)$展开：

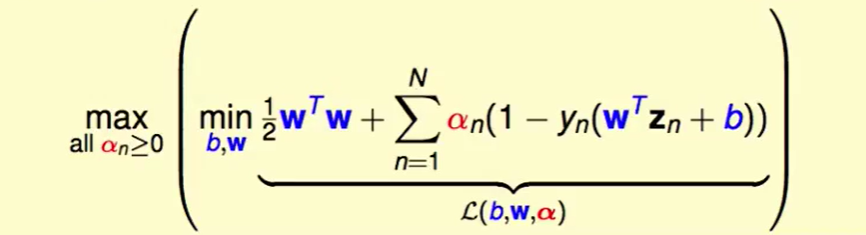
我们怎么解括号里面这个问题呢？

可以用梯度下降来做：

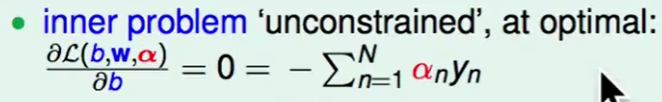
所以我们可以把这个式子作为新的constraint。

即然$\Sigma_{n=1}^Na_ny_n=0$,那么$b$就会被消掉，即问题转化为：

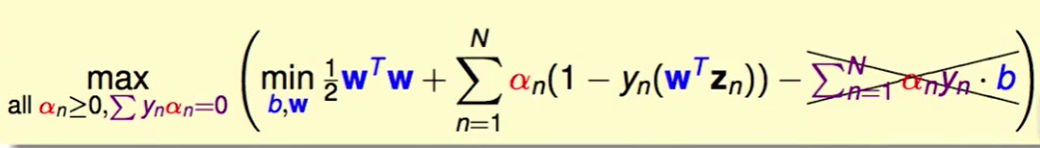
同样我们也可以对w求偏导：

那么$w =\Sigma_{n=1}^Na_ny_nz_n $ 就是一个新的constraint了。

有了上面的等式，我们可以化简为下式：

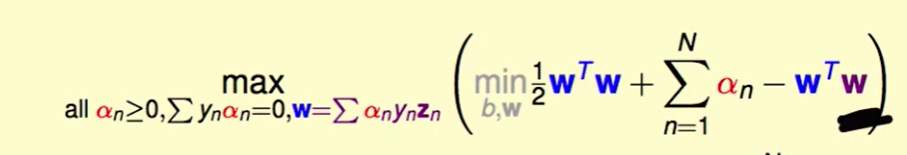
即：

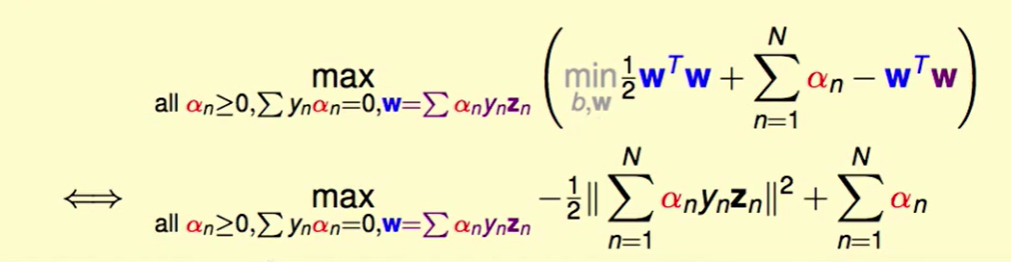
KKT 最优化的情况：

Solving Dual SVM

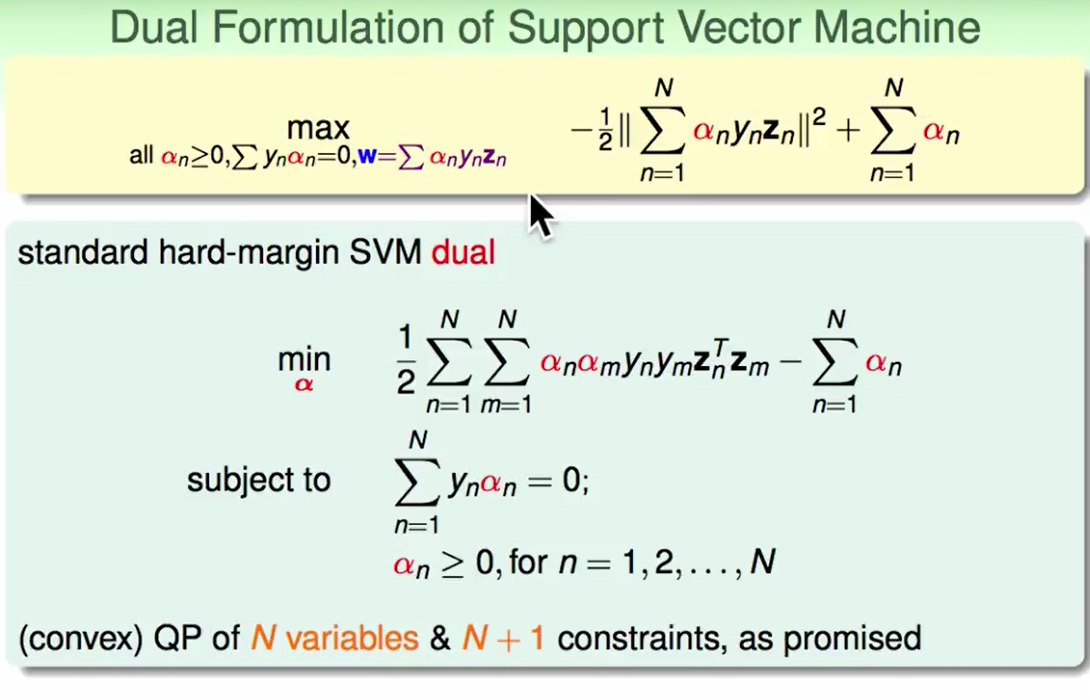
​ 我们通过转化把问题边为上图中下面的部分，这里面为什么没有加上$w$的约束条件呢？因为我们此时要解的问题是求$\alpha$, $w$的这个约束条件可以在我们求得$\alpha$后反求得$w$,但是在这里我们可以先把它隐藏起来。

​ 现在问题转化为了$N+1$个约束条件

​ 接下来我们把它转化为QP（二次规划）问题：

我们发现$Q$是一个N*N的矩阵，这就意味着：

矩阵在N=30000时就需要3G 的RAM,所以我们需要特解来解。

我们再来看KTT条件：

• $w$的计算方法：有了$\alpha$我们就可以算出$w$
• $b$的计算方法：从上面第四点可以看出，我们如果求出了一个$\alpha \ne 0$,那么$1-y_n(w^Tz_n+b)$就要等于0，我们就可以很轻易的解出$b$了。

Messages behind Dual SVM

• Dual SVM和SVM一样。

• 对于$\alpha _n>0$的点，肯定是在边界上。

• 我们称那些$\alpha _n>0$的计算结果$(z_n,y_n)$叫做支持向量（support vector）

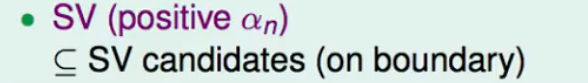
我们发现SV是SV candidates的一个子集。

而我们计算的时候只需要考虑SV，即胖胖的边上的点：

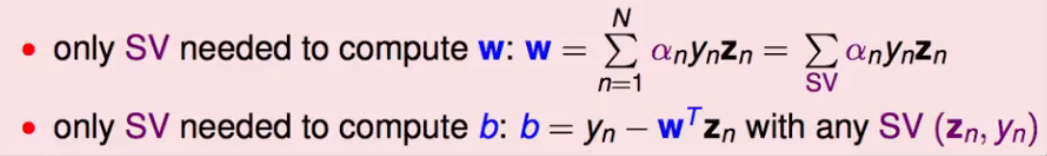
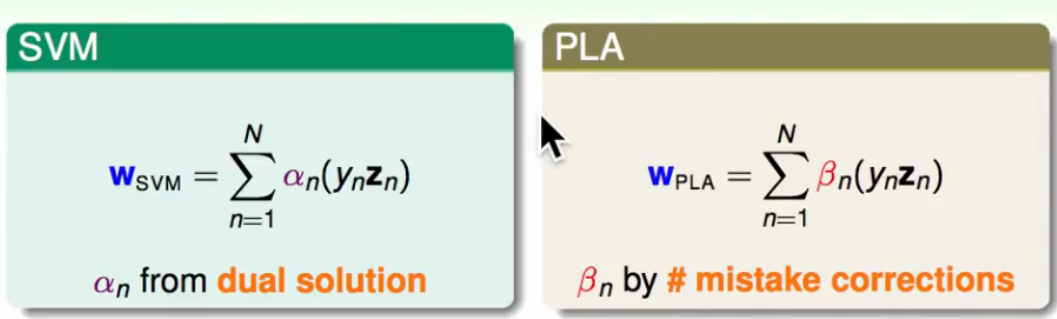
​ 当我们求得$\alpha$后，我们可以把$w{SVM}$的看作边界上点的线性组合，这个表达形式和PLA中很像，$w{PLA}$就是使得分类错误的点的线性组合，不断改正，$\beta$为调整修改的幅度大小。

总结一下：

我们对比一下原始SVM和Dual SVM的区别：

我们做Dual SVM是为了如果$\tilde{d}$很大，也就是说数据的维数很高，我们就可以用Dual SVM来做，Dual的好处就是它不需要所有数据来解，只需要SV来解。