CH3：Kernel Support Vector Machine

Kernel Trick

回顾上节的内容：

我们看似Dual SVM已经与$\tilde{d}$无关了，可是在计算时我们会发现$q_{n,m}=y_my_mz_n^Tz_m$这个式子中的$z$却包含了$\tilde{d}$, 如果这个$\tilde{d}$非常大，我们算的还是非常慢。

我们想做的是这一步，做得快一点：

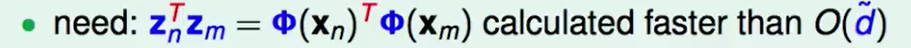
$\phi$是在做feature transform

我们考虑一个二次的转化：

这里的$\tilde{d}=d^2$, 因为他是任意两个的组合，因此如果直接算复杂度是$O(d^2)$。

我们通过上图的整理，可以把复杂度边为$O(d)$,因为我们只需要算$x^Tx’$就好了。

所以这里我们就找到了这样的一个$\phi$所对应的kernel function：

我们就可以用kernel function来做这样的事情：

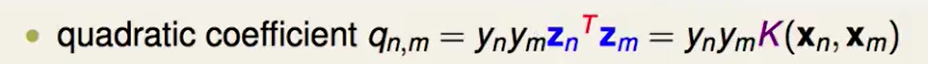
那么b怎么算呢？

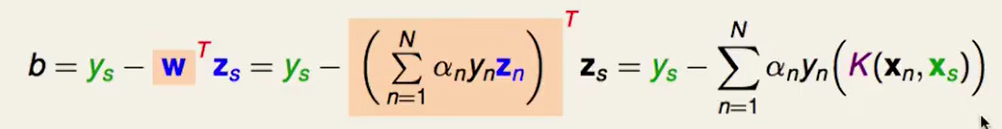
$g_{SVM}$同上，把$w^T$换掉：

最后我们把上述的总结一下：

Polynomial Kernel（多项式核）

我们因为转换到的空间相同，他们能够做的事情是相同的。

我们最常用的就是$K_2$：

但是这样的两个转换$\phi$虽然能够做的事情都一样，但是他们的内积肯定是不同的，而内积会影响margin，也就是说两个$\phi$虽然再同一个空间里，但是可能边界不相同。

比如下图，不同的二次多项式核就有不同的结果：

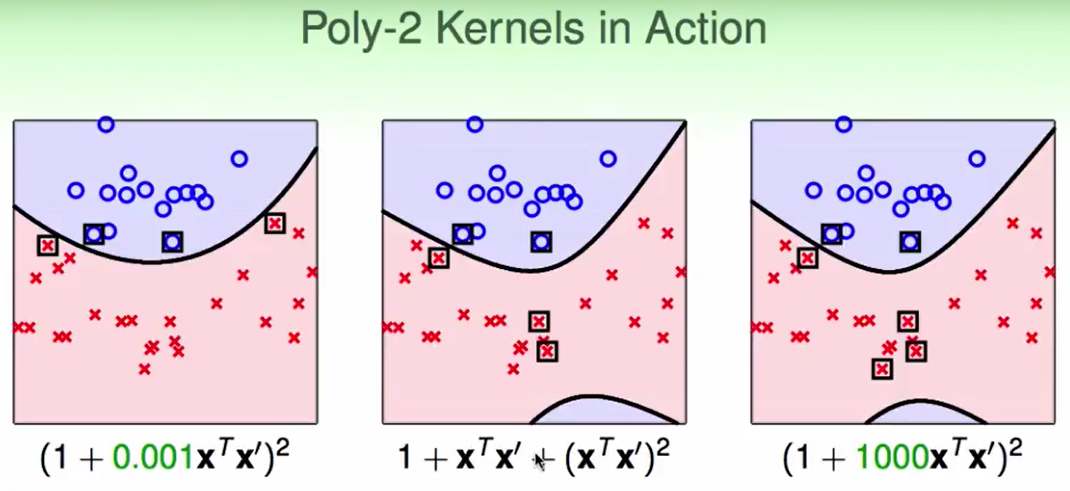
• 也就是不同的$\phi$会带来$g_{SVM}$的不同，那么他们的支持向量(SV)也会不同
• 但是我们很难知道那儿一个比较好

不同次数的多项式核：

$K_1$就是Linear Kernel：

Gaussian Kernel (高斯核)

我们现在由于计算复杂度和维度没关系了，那么我们如果做feature tranform到一个无穷多维度的空间上会怎么样呢？

我们上图把$exp(-(x-x’)^2)$看做核，然后反着取做转化，化为$\phi(x)^T\phi(x’)$的形式，那么此时的$\phi(x)$竟然代表了一个无穷多维的转化。

我们称这种为高斯核：

不同的$\gamma$可能会造成overfitting:

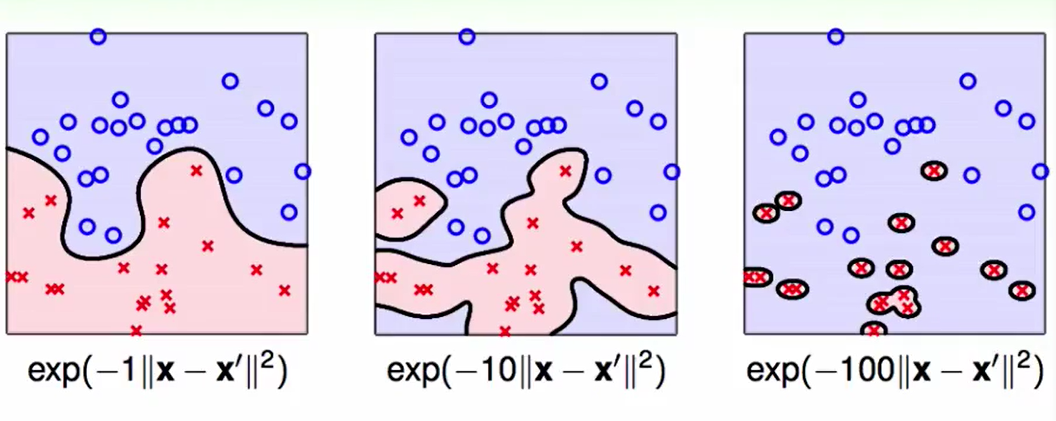
我们不建议用很大的$\gamma$。

Comparison of Kernels

我们这一节来比较一下不同的kernel：

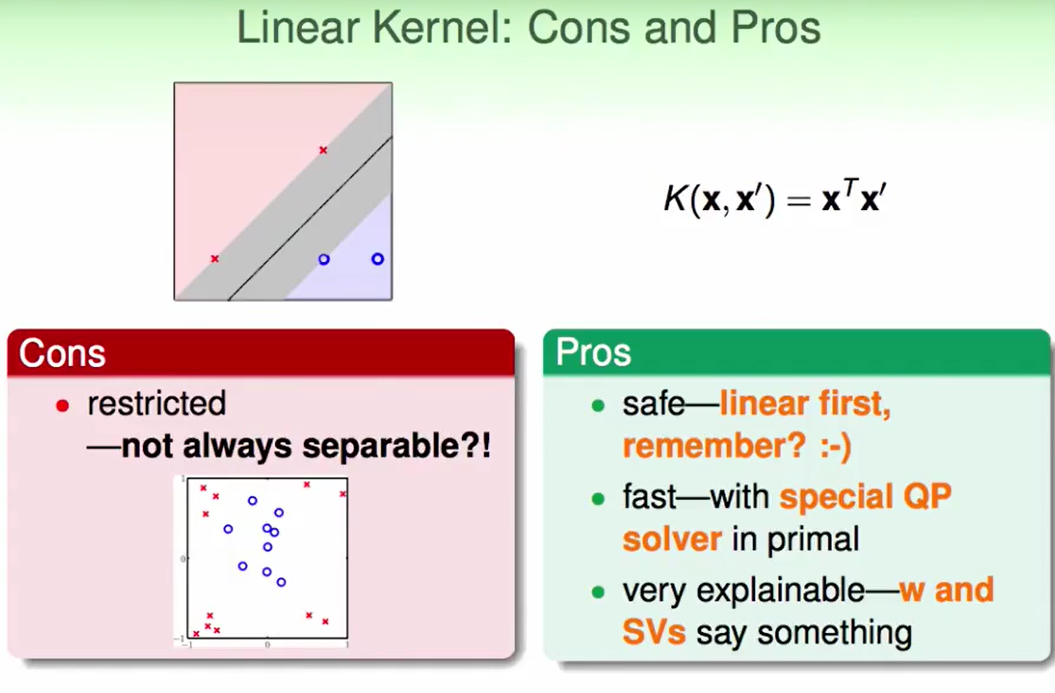
Linear Kernel：

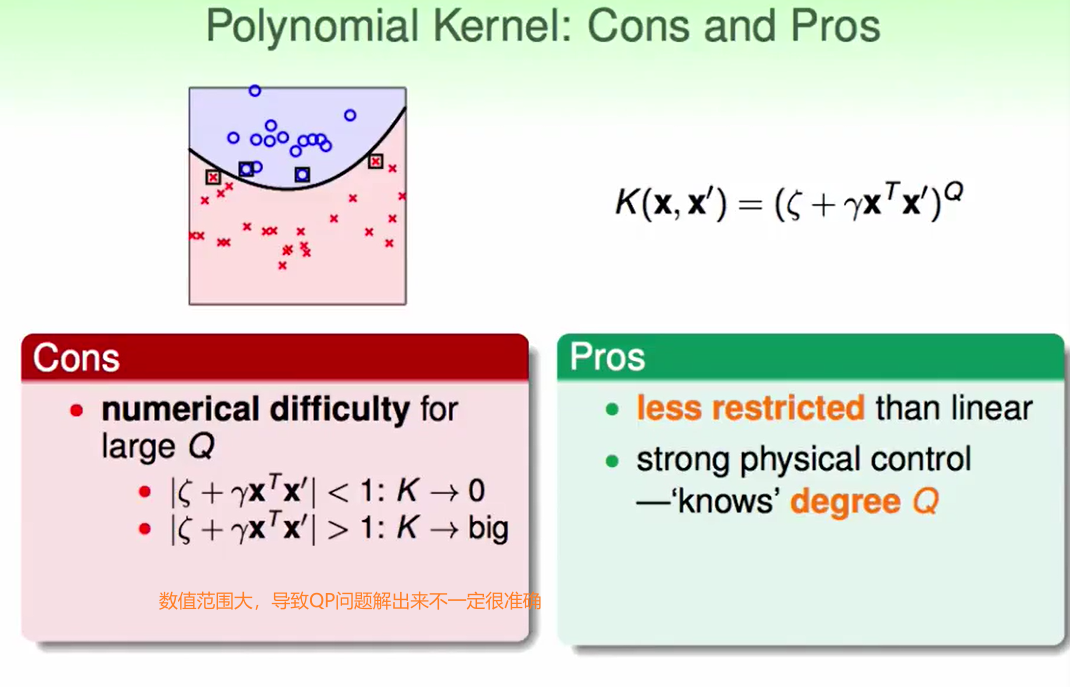
Polynomial Kernel：

Gaussian Kernel：

那我们自己可以定义一个kernel吗？

可以，但是kernel有一定的条件，Mercer’s condition就是是否为一个kernel的评判标准：