机器学习技法CH7:Blending and Bagging
CH7:Blending and Bagging
Motivation of Aggregation
现在有这样一个问题:有15个人来指导我买股票,我怎么选则是否买呢?

首先是最直观的 :选择一个以前买股票表现最好的的,也就是在做validation时最好的那一个:

让他们投票说明股票是否会涨,每个人一票:

由于一些人水平会高一些,每个人的票数不应该一样:
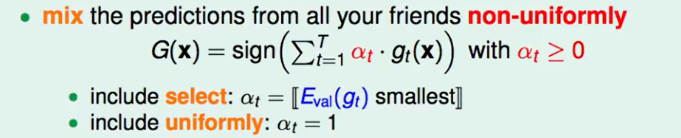
这里面是包含了以上两种的选择方式的。
有些人在某些专业领域比较在行,所以不同股票每个人权重不应该一样:
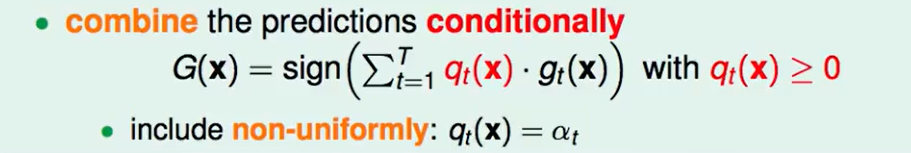
我们回顾一下select by validation:

- 简单/常用
- 我们可以用$E{in}(g_t)$来代替$E{val}(g_t^-)$, 但是这样会花费很大的复杂度代价
- 同时使用validation的时候,一般是会存在一种模型$gt^-$使得$E{val}$很小。
也就是说:

select by validation是需要有一个不错的hypothesis在set种才有意义,一堆垃圾选出来最好的也没有什么意义。
而aggregation(聚合):我们用一些一般的hypothesis来聚合成一个比较好的模型。

首先我们考虑为什么这个idea 可能work:
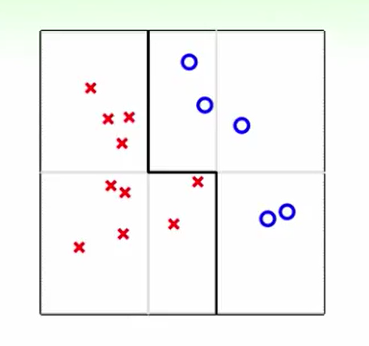
比如我们只能用垂直和水平的线来做分类,那么任何一种线似乎都无法做到完美,但是当我们把几种线聚合在一起,那么我们是有机会完美分开这两种的。

这有点类似在做feature transform。
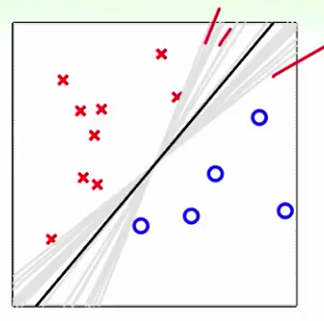
我们比如这样一个数据:我们跑PLA会得到灰色线(许多条),那么我们用aggregation来做投票后,我们得到的是一个在中间的线,这好像和SVM理论相似,找胖胖的边界,同时这也会带来regularization,容忍错误。
但是在之前的课程来看,我们基石中提到的feature transform好像和regularzation是一个矛盾的概念,因为我们认为feature transform会使得我的模型过于复杂最后overfit,从而导致容忍错误的能力差,鲁棒性差,直观反应就是regularzation没有做到。而在这里这两个概念似乎很好的平衡了。
Uniform Blending(一致融合)

一致代表着每个人都有一票,融合就是把所有人的投票都融合在一起。

这个的$G(x)$定义就是 比如有K个类别的结果,我们投票发现那儿一类得票数最多,最多的作为最后的投票结果。
那么在regression问题中uniform blending得到的$G(x)$一般长这个样子:
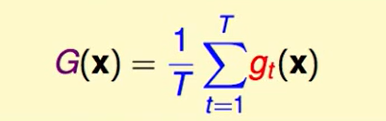
我们考虑对具体某一种输入$x$来看,他们的squre error的区别:
每个人预策结果和真实结果的squre error的平均值 与 每个人平均预策结果的平均值和真实结果的差值 的大小关系

这是对某一个$x$的得到的结果,如果是所有的$x$,那么就得到如下的式子,其中$\epsilon$表示期望。

这样告诉我们,我们里用uniform blending求出的G去做预测的错误率真的会小于随便选一个$g_t$去做预测的错误率低。

我们进行T轮迭代:
每次迭代都是新的N个数据,用算法来求出$g_t$,如果迭代T轮后我们就有T个$g_t$,于是我们可以求出一个$g_t$的平均作为$G$.
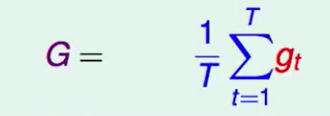
如果我们的迭代轮数T趋于无穷,那么:
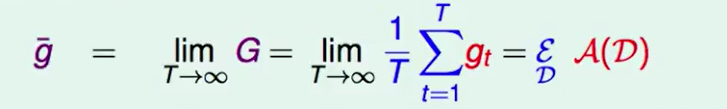
因此这是一个g的平均就是 = 产生资料过程的平均。

- $avg(E_{out})$就是算法$A$得到的结果的期望
- $E_{out}( \overline{g})$表示着各个hypothesis给出的结果的综合表现
- $avg(\epsilon(g_t - \overline{g}))$ 表示上述两个结果 的偏差
当 偏差消失,我们的算法得到的结果就会变好。
Linear and Any Blending
Linear Blending是这样的一个问题:

怎么样的$\alpha _t$的选择才是好的呢?
一个直观的想法就是我们取得这个最好的$\alpha$后我们可以得到最低的$E_{in}$。
Linear Blending 来组测回归问题就是:
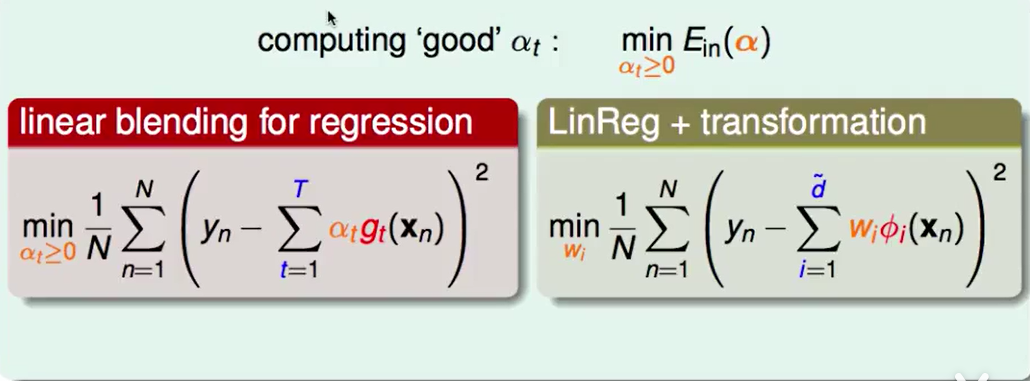
LinReg+feature transform似乎和他长得很像
我们可以把linear blending 看作 线性模型上加上一个feature transform,并且还有一个限制 那就是$\alpha\ge0$

如果没有这个constraint,我们可以直接用Linear regression那一套同样的方法计算即可,但是现在我们有这个constraint,他有什么作用呢?

如果对于一个$\alpha<0$,我们可以转换为$|\alpha_t|(-g_t(x))$, 可是这样的转换会让这个$-g_t(x)$在预测时分类得到相反的结果,然而对于二分类来说,这种是无所谓的,我们看反面即可。
因此我们可以忽略constraint。
我们比较一下 Linear Blending 和 Seletion的区别


Selection by $E{in}$ :这种方法我们首先是在不同的hypotheset中分别训练一个最好的g,然后用分别用自己得到的 $g$ 算$E{in}$, 找到一个最小的$E{in}$作为我们最好的g,这是一种best of best的想法,付出的代价是$d{VC}(\cup_{t=1}^T H_t)$
Linear Blending:这种方法是找一个最好的 $\alpha$ 使得使得$E{val}(g_t^-)$最小。复杂度是Linear blending with $E{in}$, 也就是aggregation of best,把最好的汇聚在一起,这个复杂度是大于Selection by $E_{in}$的。
- 像selection方法一样,我们的blending方法经常用$E_{val}(g_t^-)$
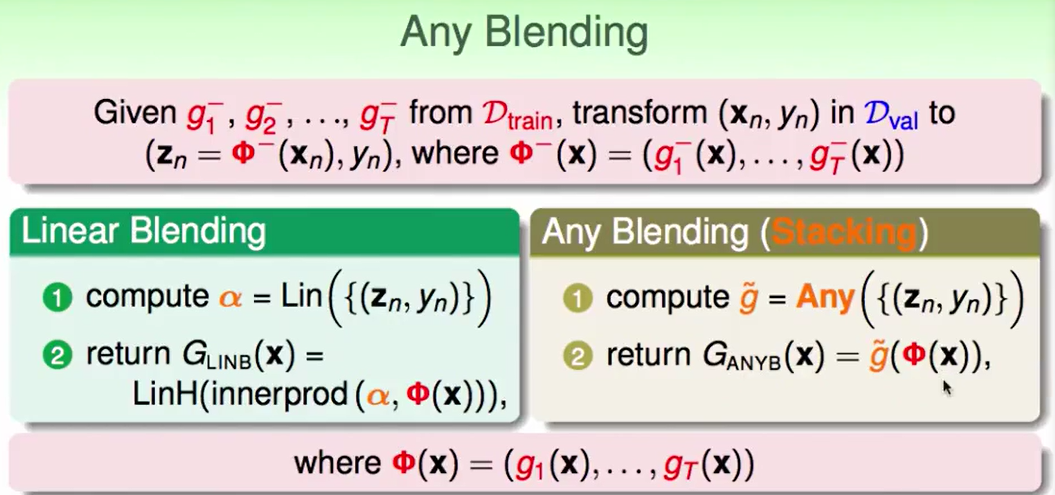
如果我们可以做到Linear Blending,那么我们就可以做到any Blending

Bagging(Bootstrap Aggregation)

我们现在是学习完所有的$g$后开聚合,那么我们可以边学边聚合吗?这是我们接下来要考虑得问题。

我们不一样的$g$可以来自很多方面:
- 模型不同得到的$g$不同
- 不同的参数得到的$g$不同
- 算法本身就带有随机性,每次得出来的$g$不太一样,比如PLA的起始点不同
- 数据的随机性,比如within-cross-validation 通过不同的$g_{val}^-$肯定得到不同的结果
如果我们就这有一份资料,想做blending,也就是说我们想过一份资料做data randomness得到不同的数据,用这些数据做blending,但是我们不希望用$g^-$的方法,因为这种方法得到的$g-$是比较次级的。
我们回顾一下上节的问题:

也就是说一堆$g$的共同作用来判断的效果是好于单一的一个$g$来做判断的期望效果。
但是这是有一个前提的:
首先迭代次数要趋于无穷,这里我们妥协一下,T改为一个很大的数,但是是有限的
其次,我们要保证资料是新鲜的,每次都从分布中得到新的资料,而我们现在只有一笔资料,这里我们可以用bootstrapping这个方法。
bootstrapping:

这其实是一种统计学里的方法,这种方法就是有放回的抽取N个资料,每次抽取分别作为第$1,2,3…..T$笔训练资料。

上图是一个实际的aggregation的方法和bootstrap aggregation的比较。

bootstrap aggregation也叫 BAGging,
bootstrap aggregation就是一种先用bootstrap生成许多组的数据,然后用uniform的方法合起来。
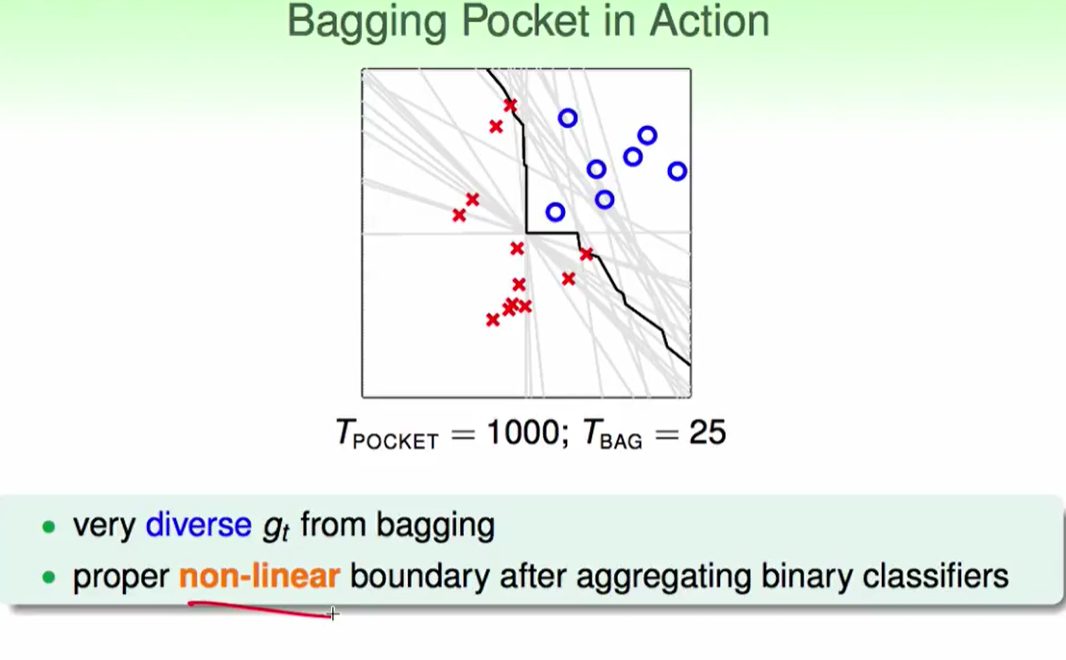
如果我们的algorithm对data randomness很敏感,那么我们就可以通过bootstrap得到较高质量的不同数据,此时我们的bagging效果会比较出色。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!