机器学习技法CH8:Adaptive Boosting
CH8:Adaptive Boosting
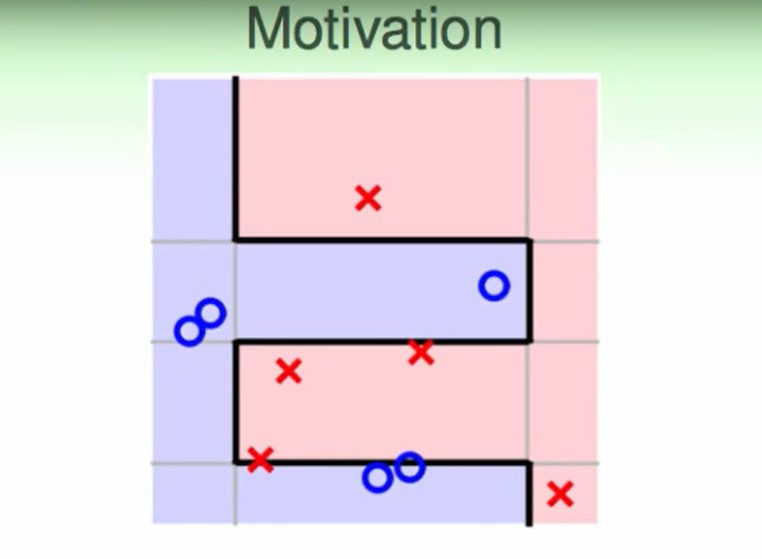
Motivation of Boosting
我们假设一个老师教学生认苹果的场景:

其中上半部分是苹果,下半部分是其他水果。
1.首先A提出按照形状判别苹果:

那么A做对了一部分,但是蓝色方块的水果里判别犯了错误。
2.我们为了减少这些错误,我们可以把已经做对的变得小一些(表示我们减轻一些对这些图片的注意力,着重看我们犯错的地方)

我们又提出一种判别的方法:红颜色的是苹果

但是这种方法在其他地方又会在蓝色部分判断错误。
3.我们重复第二步,放大错误,缩小正确的。

我们提出新的判别方法:苹果是绿色的。
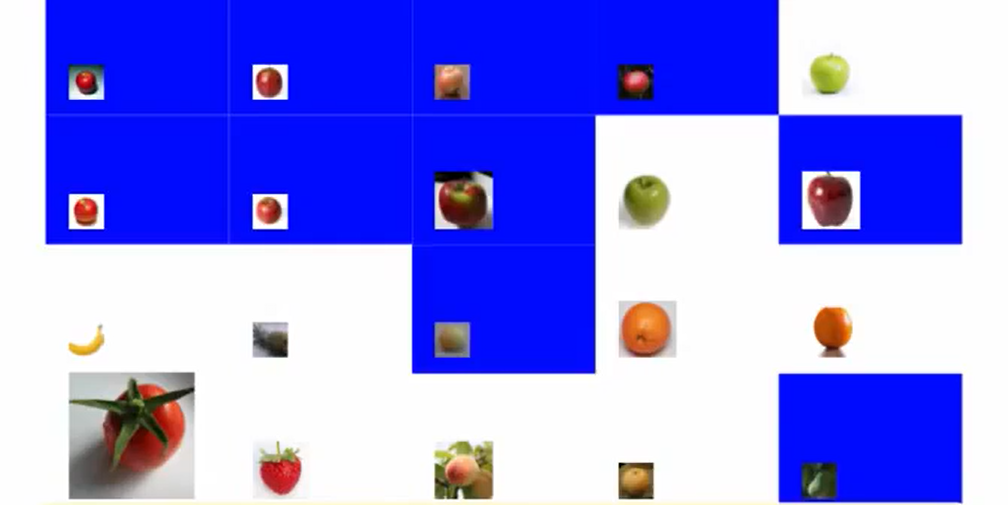
我们此时犯了一堆错误,但是请注意,我们犯错的都是我们注意力已经下降的图片了,在主要的注意力上,比如右下角的番茄被判别正确了。
4.和上面一样,蓝色部分(错误的)放大,再找新的规则来判别:苹果有梗

以此不断重复。
这就像一堆二元分类的classifier的aggregation。
老师给出的指导就是让我们focus on key example
Diversity by Re-weighting
我们首先回想一下Bagging算法,首先做bootstrap:
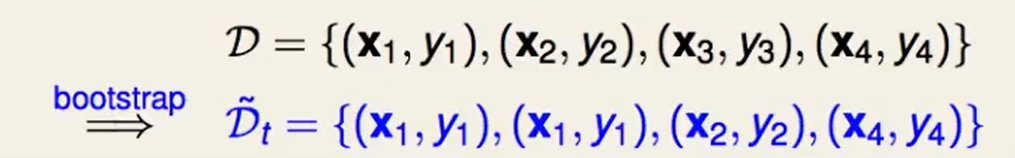
然后我们找出每个$gt$通过使得该份数据都最小化$E{in}$来得到。

其实我们可以换一种写法,我们用$u_t$代表第$t$个数据的重复次数:


这里面的$u$的概念可以代表这个点的权重:
我们提出weighted base algorithm

我们可以把这个问题转化为一个SVM问题:

也可以转化为一个logistic regression问题:

在aggregate里我们提到过:我们希望$g$之间越不同越好,也就是$g$多样性一些,因为这说明着我们学到了新的特性。
我们怎么才能使得$g$有一些多样性呢?
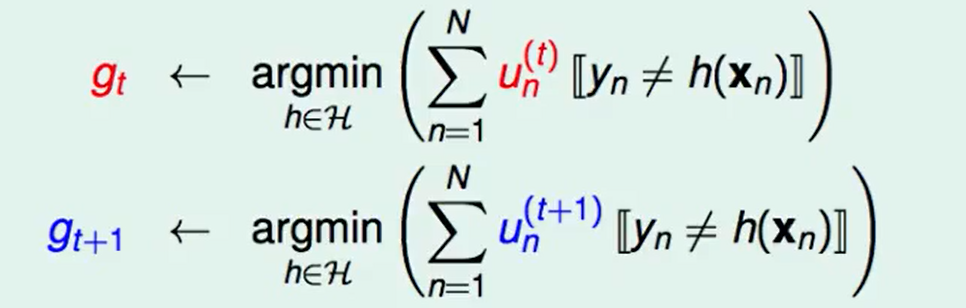
我们比如现在用$un^{(t)}$和$u_n^{(t+1)}$两份数据分别来训练$g$并得到$g{t}$和$g_{t+1}$,我们希望的多样性就是指这两个预策的结果不是很像。
那么现在假设我们已经有$gt$了,我们想要获得一个新的$u_n^{(t+1)}$来使得训练得到的$g{t+1}g_{t}$不太一样:
我们怎么数学的去衡量这个不一样呢?
我们用$u_n^{t+1}$这个权重去计算$g_t$算出来的判别结果来加上权重,这样算出来的错误率如果能达到$1/2$,那么说明已经长得很不一样了,因为这样计算出来的错误率和瞎说判别结果得到的错误率已经没区别了(几率都是$1/2$),那么此时用这个$u_n^{t+1}$去训练数据一定可以得到一个和$g_t$相差比较大的结果。

现在的问题就是我们希望怎么到达这个$1/2$.
我们拆开来看这个式子,就是计算错误的次数

我们希望在$u_n^{t+1}$的数据下用$g_t$来预测,最后得到结果这样的结果:错的数据数 占 总数据数的一半。那么怎么调节呢?

比如我们在$un^{(t)}$下我们错误数是1126,正确数是6211,我们调整一下下一次的权重对于犯错的点权重调整为:$u_n^{(t+1)} = u_n^{(t)}6211$,同理,对于正确的点调整为:$u_n^{(t+1)} = u_n^{(t)}1126$。我们就可以得到一个全新的$u_n^{(t+1)}$,这个就保证$g{t+1}$和$g_{t}$的不同。
Adaptive Boosting Algorithm
我们把上节最后的内容用一个scaling factor来统一下这样的操作:

这个scaling factor 很好的统一了两种操作。

就像这个放大错误就像是第一节老师所起到的作用一样。
我们现在提出我们的算法的一个大致思路:

但有两个问题:
$u^{(1)}$怎么选择呢? 我们想让$g_1$表现最好,一个比较直观的就是让$u_n^{(1)} = 1/N$.也就是我们不做干涉。
那我们怎么得到$G(x)$呢?也就是怎么融合得到的$g$呢?
- uniform ? 这不是一个很好的方法,因为我们前面已经说了,$g$和$g$之间差别很大,这样得到的效果会很差
- 我们可以linear,no-linear的来组合
- 其实我们可以用一种特别的算法来aggregate这些$g$, 并且还是linearly,实时的来aggregate这些$g$。
我们希望这种算法是:

这种算法可以边算$g$边给出权重$\alpha$.
- 我们希望好的$g$占的权重可以大一些,我们可以让$\alpha_t=ln(♦_t)$:
- 错误率$\epsilon_t=1/2 \to ♦_t=1 \to \alpha=0$ :也就是说表现差的g不要,权重是0
- 错误率$\epsilon_t=0 \to ♦_t=∞ \to \alpha=∞$ :也就是说表现完美直接权重拉满!
因此Adaptive Aggregation的算法是:

其实这个算法就是三部分组成:

比较弱的算法$A$,老师进行权重调整,最后aggregate到一起。
AdaBoost的理论保证:

- AdaBoost的作者给出了迭代$logN$轮后即可让$E_{in}$几乎等于0
- 我们把$T=logN$带入VC bound后半部分的式子就会发现后半部分式子很小
- 这样VC Bound就告诉我们,AdaBoost算法让$E{in}$几乎等于0,并且还可以得到很好的$E{out}$
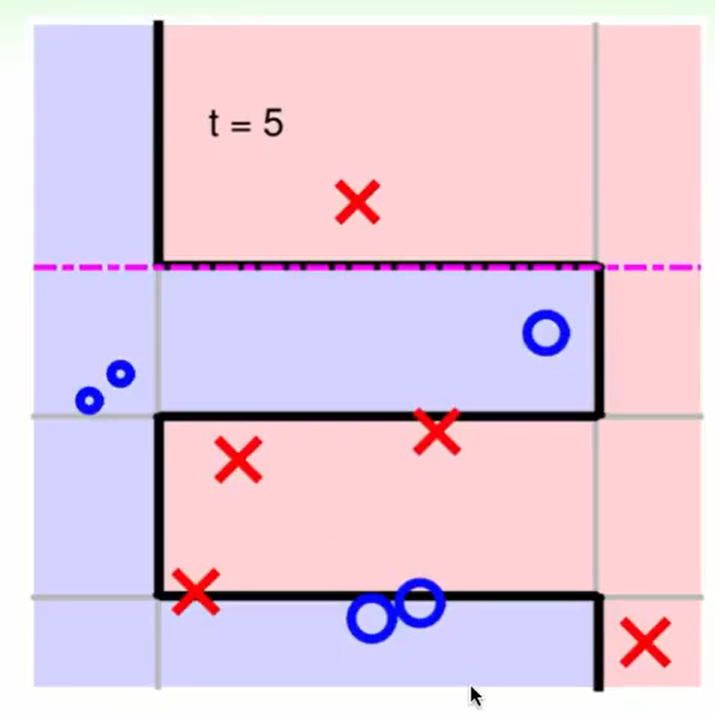
Adaptive Boosting in Action
回到上次的AdaBoositng算法:

我们希望让找一种比较弱的算法,可以使得表现的效果过好一点,但不用特别好,因为我们上节提到,几个比较准确率大于$1/2$的算法就可以aggregate一个不错的算法了。

一种比较常用的方法是:decision stump

这种方法是:在不同维度的feature上做简单的二元分类,分割线在二维面上只有水平/竖直 分割线。
但是效率非常高: 每次我们对每个维度去排序$O(NlogN)$,然后$O(n)$去遍历最好的分割点,对每一个维度都这么操作,$d$个维度,那么复杂度就是$O(d*Nlog N)$
举个例子:
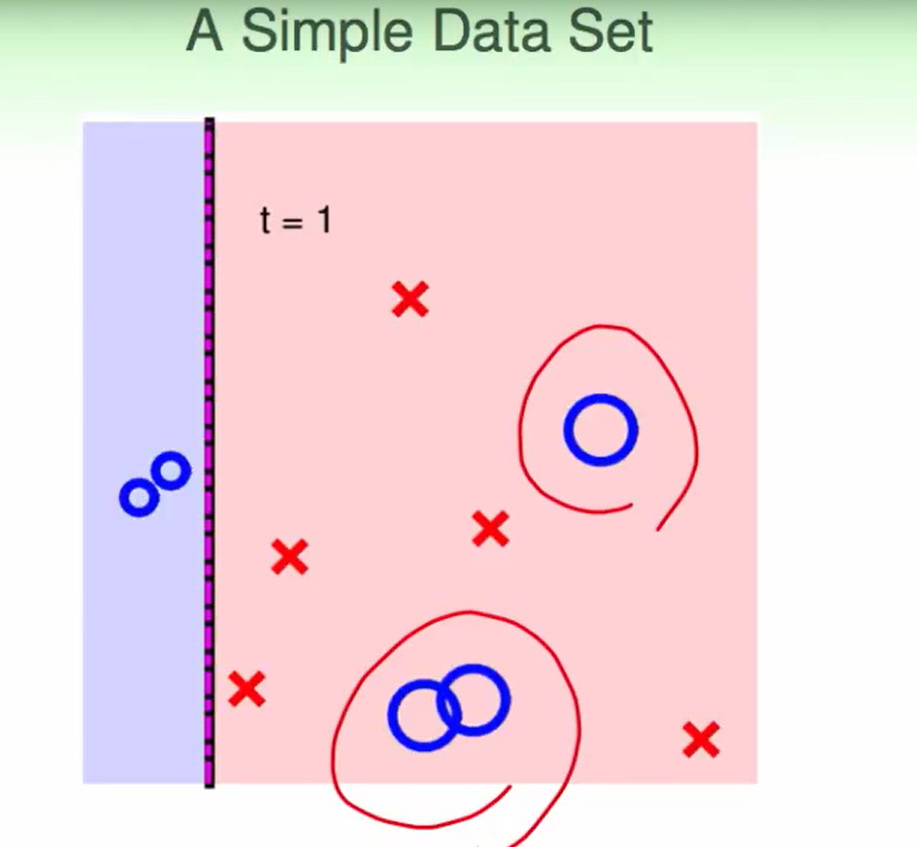
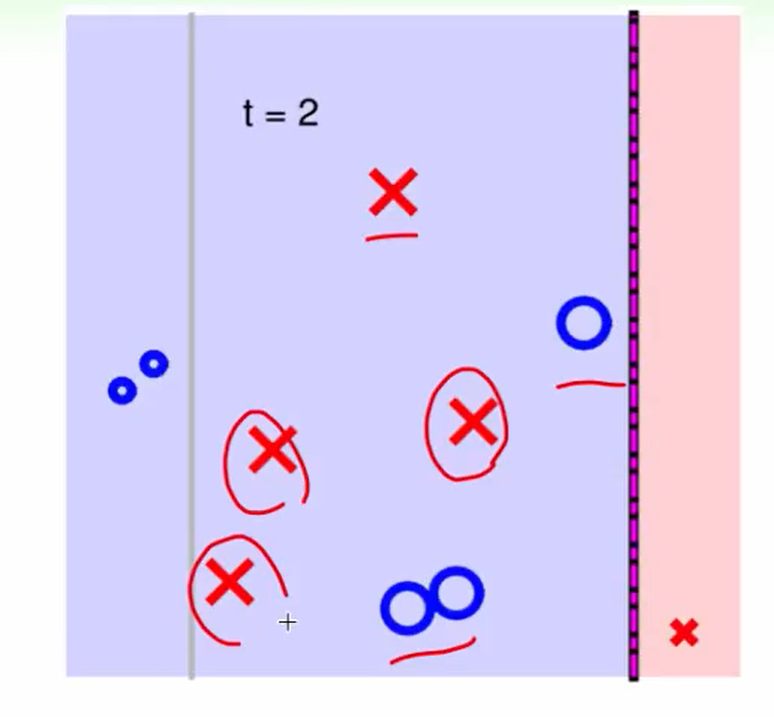
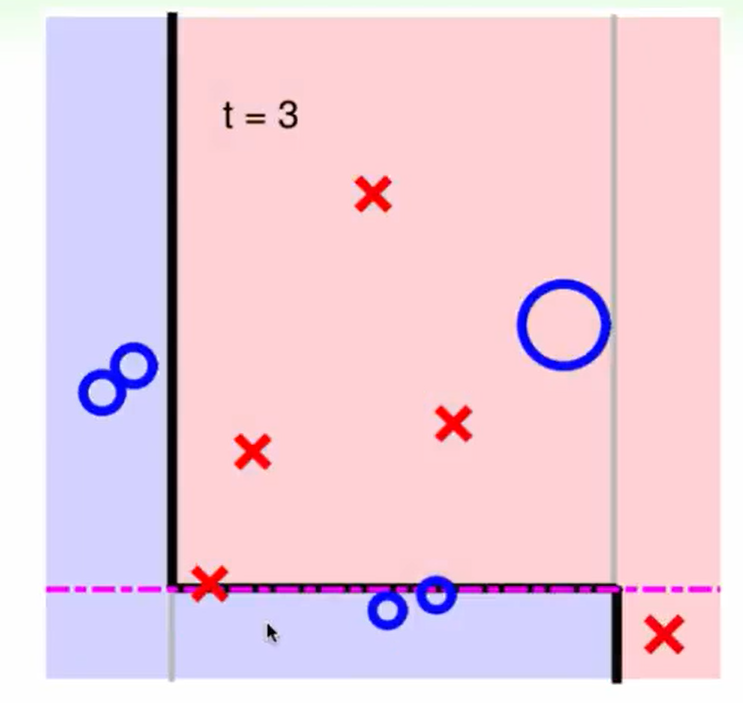
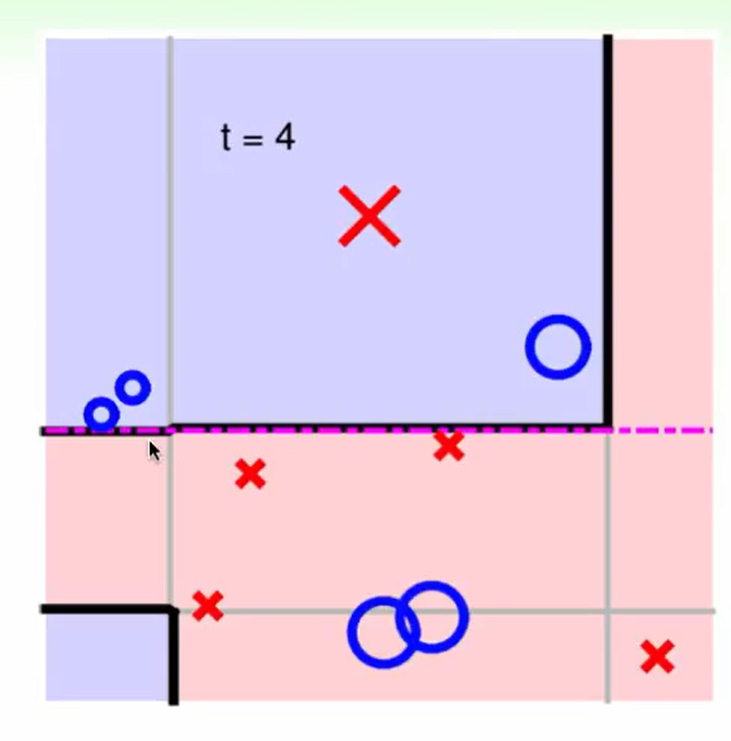
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!