CH9：Decision Tree

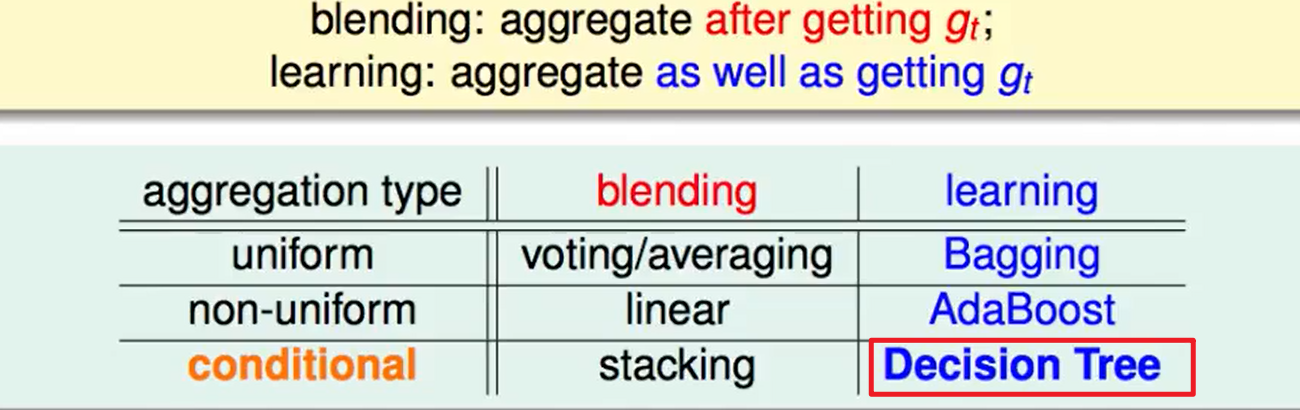
Decision Tree Hypothesis

一个decision tree的例子：

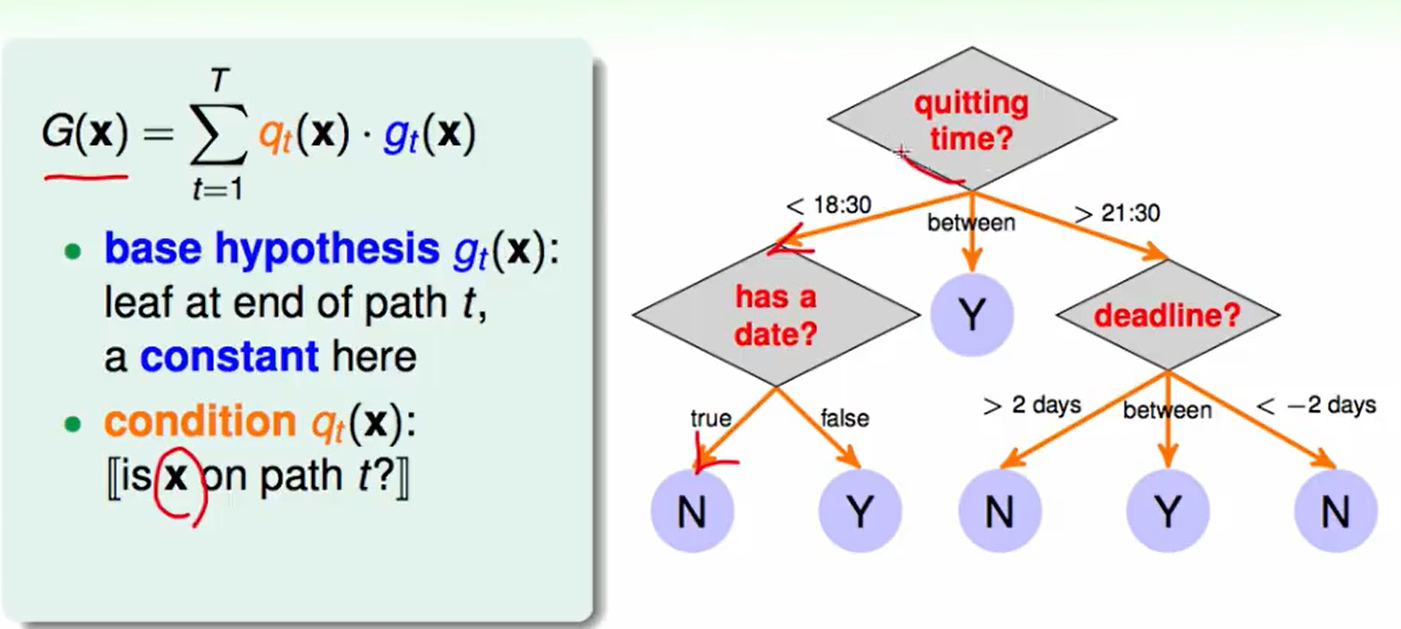
• $g_t(x)$：称为base hypothesis，叶子节点，一个常数，代表路径$t$的终点的常量，也就是最后做的决定。
• $q_t(x)$: 称为condition， 判断$x$是否在路径$t$上。

我们可以把一棵树看成如下的样式：

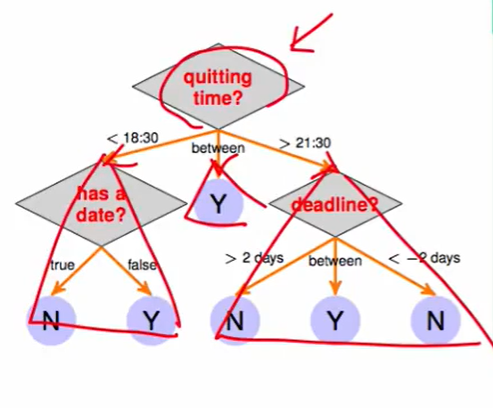
那么上图这种一个节点对应着三个子树，然后在子树中可以接着递归找子树。因此我们还可以用递归的来定义这个决策树：

• $G(x)$ 一个树
• $b(x)$分支条件
• $G_c(c)$:第c个分支条件通向的子树

decision tree的优点：

• 可解释性强，常用在医学等模型上。
• 简单，只是一个树递归
• 高效，判断的复杂度是log级别的

缺点：

• 没有很强的理论解释/理论支持
• 实际应用中依赖启发式的选择，需要灵感。

Decision Tree Algorithm

这个算法很容易写出一个basic的版本。

但是我们要做四个选择

• 分支有多少
• 依赖什么因素来分支
• 什么时候停止
• 回传的constant是什么

下面介绍一种常用的decision tree：Classification and Regression Tree(C&RT)

• 这个tree是一个binary tree，每个结点只有两个分支。

• 对于叶子节点的值怎么设定呢？

  • 对于classification任务(0/1 error)：我们用一组已经知道label的资料放进去跑decision tree，落在叶子节点后计数，看看每个叶子节点里1多还是0多，取多者为叶子节点的constant，即取最多的$y_n$。
  • 对于regression任务(squared error)：取$y_n$的平均即可。

除了上面的 如何设置分支也是很重要的一部分：

C&RT的划分方法：

• 用Decision Stump来划分：对feature的每个维度划分，那么一共可以有$d$个binary decision。
• 依靠purifying(纯度)来决定分支：

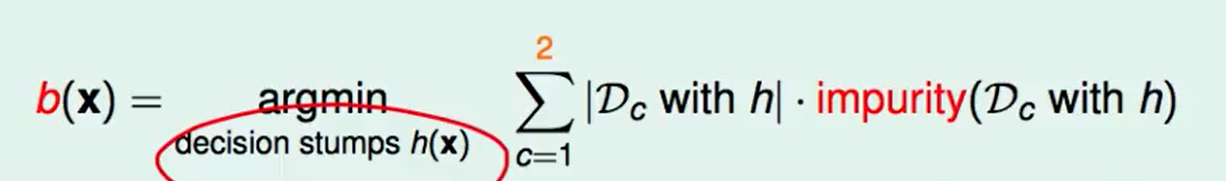
对于每个binary decision，也就是一个$h$ ,我们考量他的得分$b(x)$，思路很简单，就是对于$h$分割开的两份我们分别去算各自那一份的不纯度，然后乘上那一份的大小，这个做法很符合直觉。

上述的$impurity$函数选择有下面几种：

首先可以通过$E_{in}$来选择。

对于classification错误，我们也可以用这几种：

实际应用这 在regression中常用regression error，在classification中常用Gini index

最后一个问题就是：什么时候停止？

Decision Tree Heuristics in C&RT

C&RT算法总结：

二元分类任务可以很简单的完成，同时如果是一个multi-classification的任务，我们对上面的算法只需要constant改一下，impurity的计算公式改一下就可以做多分类问题了。

但是我们注意到了一个问题：

这个算法里要求最后是fully-grown tree，即$E_{in}(G)=0$, 但这样很有可能最后overfit。

• 我们需要一种regularizer,一种简单想法：控制叶子节点的数量。

• 然后我们去做正则化：

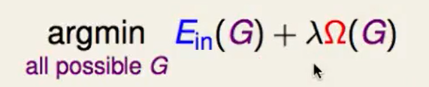
• $\lambda$怎么选择：validation

通过$\lambda$来平衡这件事情，我们称这种decision tree为pruned decision tree

但是这个方法操作起来没那么简单，我们考虑的是all possible G，那种类可就太多了，所以我们考虑这么做：

• 先做一个fully-grown tree，作为$G^{(0)}$.
• 然后对这个G(0),每次去掉一个叶子节点，计算$E{in}$,然后先放回去，接着再选一个叶子节点去掉，我们找这里面$E{in}$最低的一种删除掉，作为$G^{(1)}$
• 以此循环

如果我们有一些资料缺少了一些feature，我们可以用其他相似的feature 来替代：

比如体重数据缺失了一部分，可以根据身高的threshold。

Decision Tree in Action

举一个例子：

第一次：

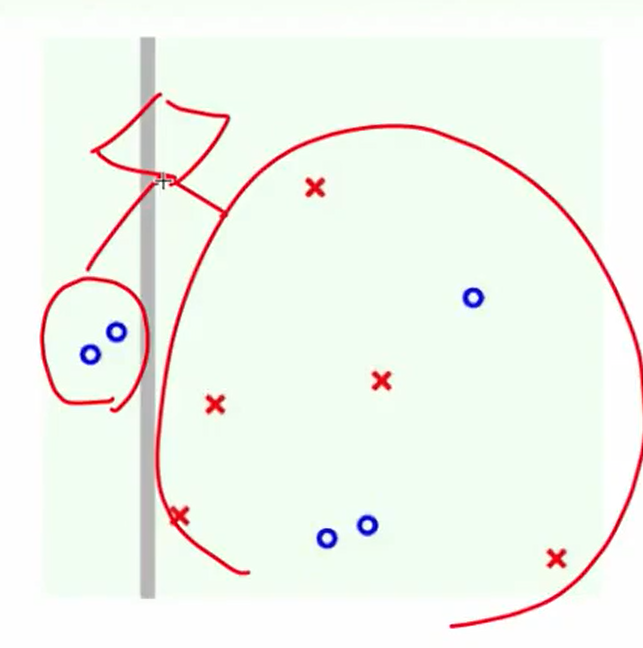
第二次：

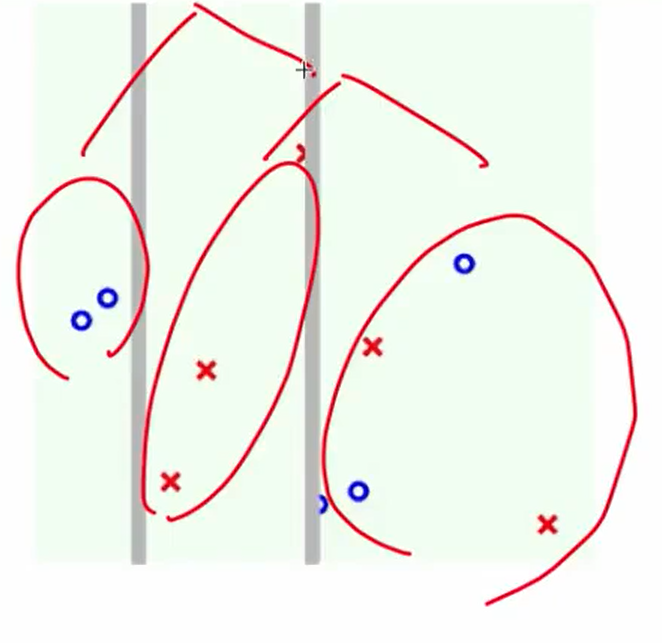
第三次：

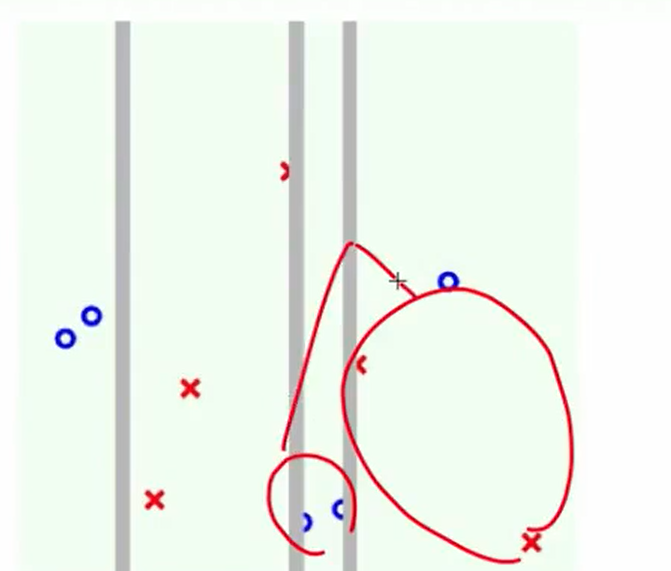
第四次：

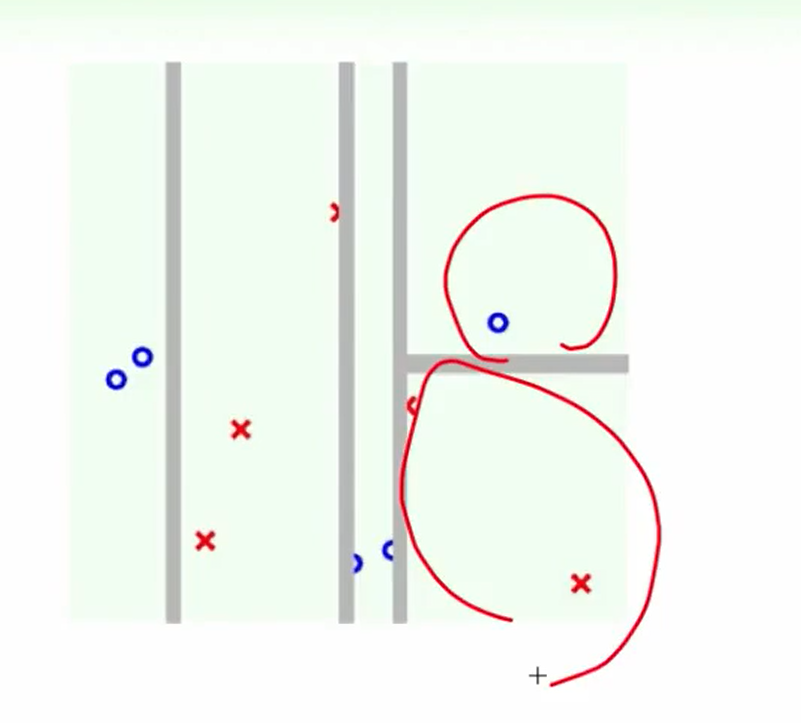
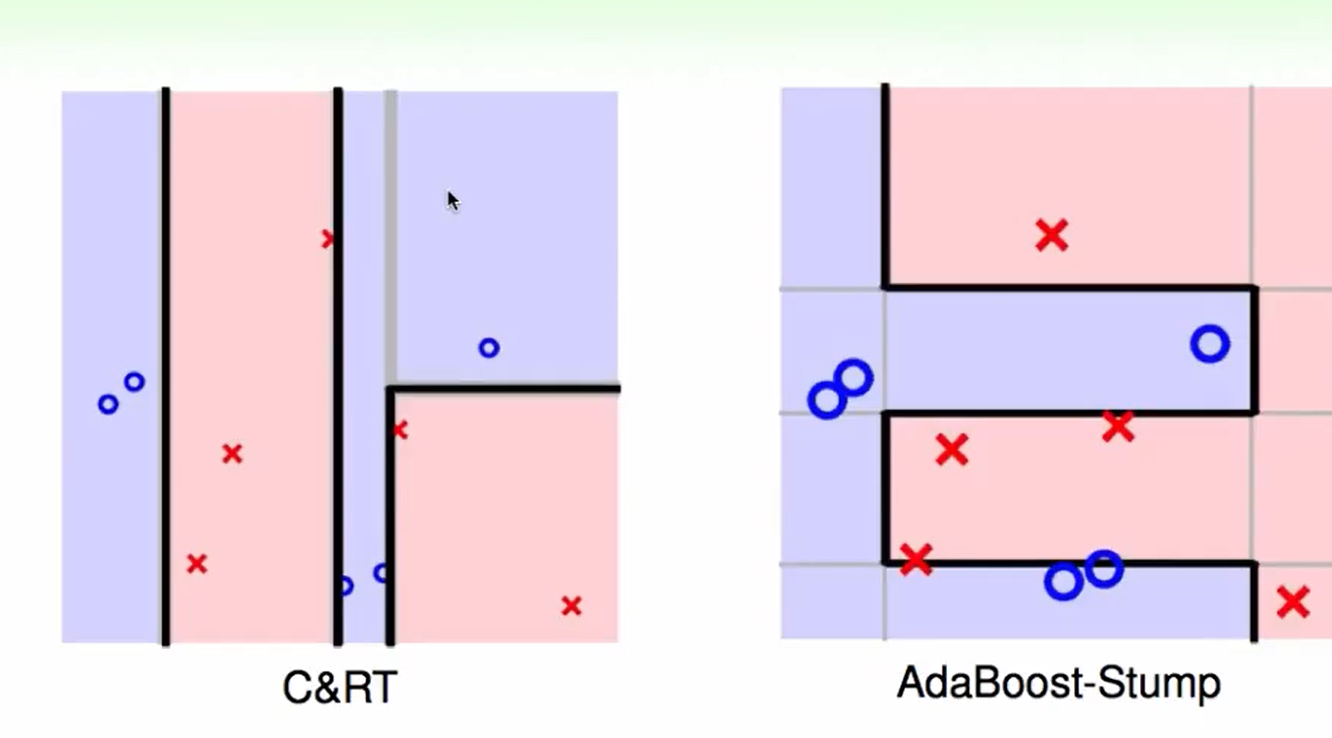
我们可以看出区别：AdaBoost切的都是贯穿全局的，而C&RT可以由于在子树里切，因此可以切一部分

当数据多的时候，我们会发现C&RT效率会高一些，因为它可以切一小部分。

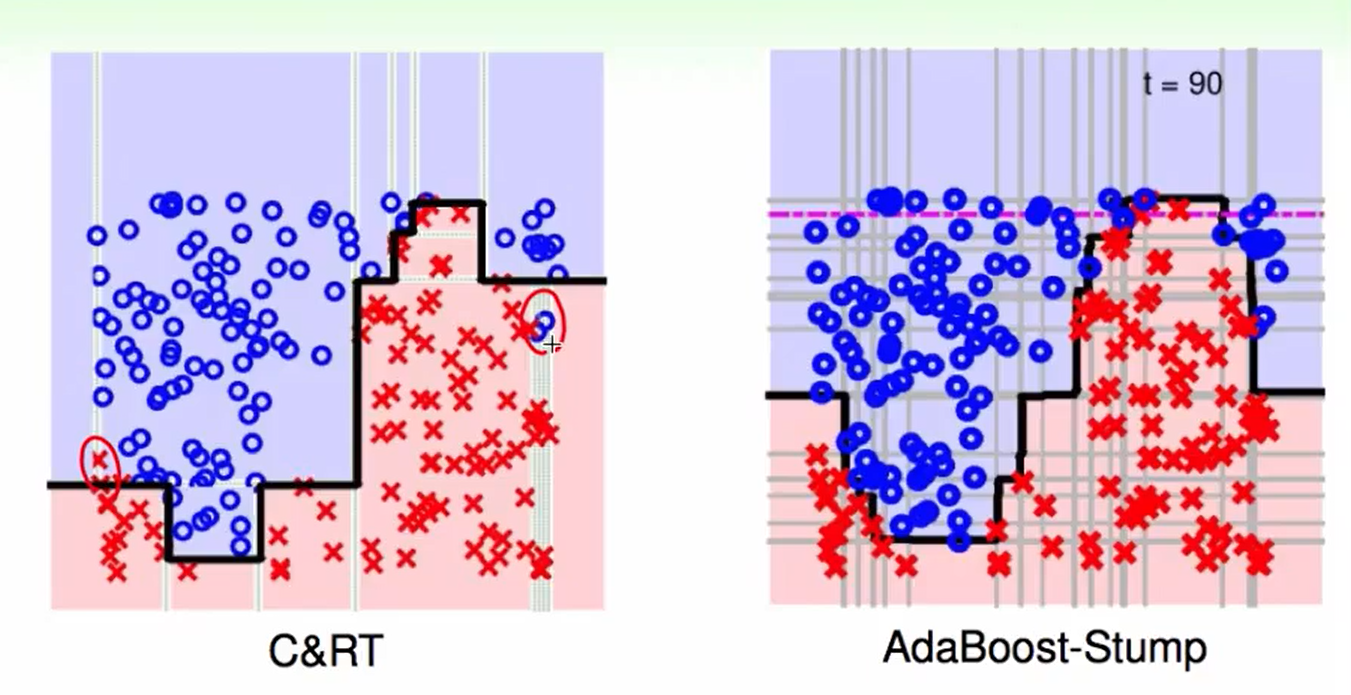
Decision tree 优势：