CH10：Random Forest

Random Forest Algorithm

首先回顾：

random forest是两部分组成：

流程是：

• 首先对数据做bootstrap，处理数据
• 然后用处理完的数据去跑decision tree，获得很多个$g_t$
• 最后uniform的合并这些树，也就是uniform的合并$g_t$

这个算法的特点：

• 我们可以看到用decision tree处理数据的时候，不同份数据没有关系，所以可以并行计算，很高效

• 还有就是random forest 继承了C&RT的优势：可以处理multi-class的数据

• C&RT由于时fully-grown tree可能回overfit，但是bagging会大大的减轻这种情况。

我们合起来这些树的时候，希望这些书很多样性，除了我们bootstrap做出来的数据可以帮助多样性外，我们还可以对数据的feature下手，比如feature 的维度是$d$，我们可以随机抽$d’(d’<d)$个维度(即抽一个feature的子集)来做C&RT decision tree。

即：

除了这个random特性，Random Forest还有一个random的特性：

已经抽取后的$d’$维数据，我们在给他乘上一个投影矩阵，其中投影矩阵的每一行从基向量随机抽出来

这种方法使每次分支得到的不再是单一的子特征集合，而是子特征的线性组合（权重不为1）。好比在二维平面上不止得到水平线和垂直线，也能得到各种斜线。这种做法使子特征选择更加多样性。值得注意的是，不同分支$i$下的$p_i$是不同的，而且向量$p_i$中大部分元素为零，因为我们选择的只是一部分特征，这是一种低维映射。

Out-of-bag Estimate

Bagging中bootstrap用图来表示就是下面这样：

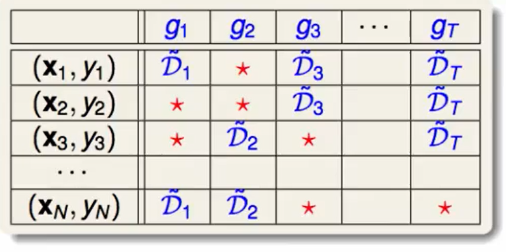
他代表了我们训练的$g$是由哪儿些数据训练出来的，红色的$*$代表这个数据在这个训练中没有被用到，用到的就会放入到$D$中。

我们称这些红色的$*$为：$g_t$的out-of-bag数据

对于一个数据$(x_n,y_n)$来说,他成为out of bag的几率是 $(1-1/N)^N$,其中N是抽出来的数据的数量。

如果$N$足够大，那么一个数据成为OOB的概率就是$1/e$。也就是说我们的数据有$1/3$是没有被用到的。

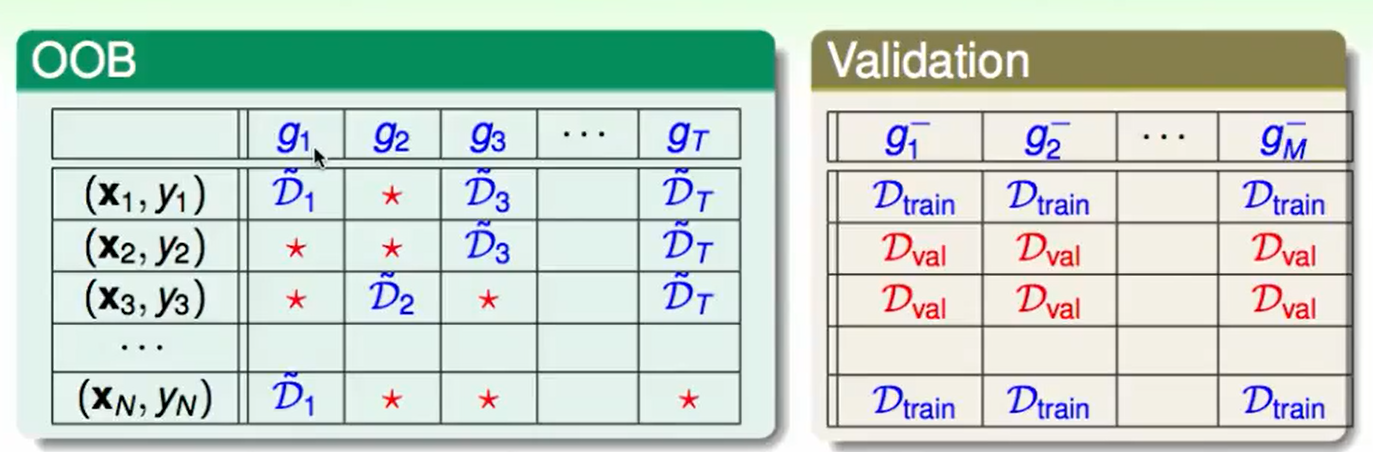
我们有$1/3$的资料没用，那么我们有这个做validation不就好了吗？

• 我们用OOB来验证$g_t$？其实是不需要的，因为我们并不关心$g_t$做的怎么样，反正最后aggregate在一起效果好就行。

• 但是我们需要用OOB来验证$G$(最后把$g$ 合并在一起的函数)，在blending或者random forest中的decision tree中我们会遇到一些参数，这些参数选择的怎么样，我们可以用OOB来验证。

比如资料$(x_N,y_N)$他在$g_1$中被用到了，但是在$g_2,g_3,g_T$中没有被用到，所以我们可以说用$g_2,g_3,g_T$组合成的$G_N^-(x)$来做validation，

对每一个数据都这么做，有点类似于one-versus-all validation

最后得到这个错误率：

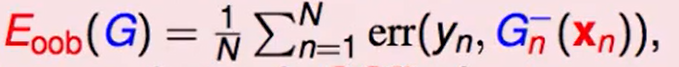
我们和之前的validation再观察一下区别：

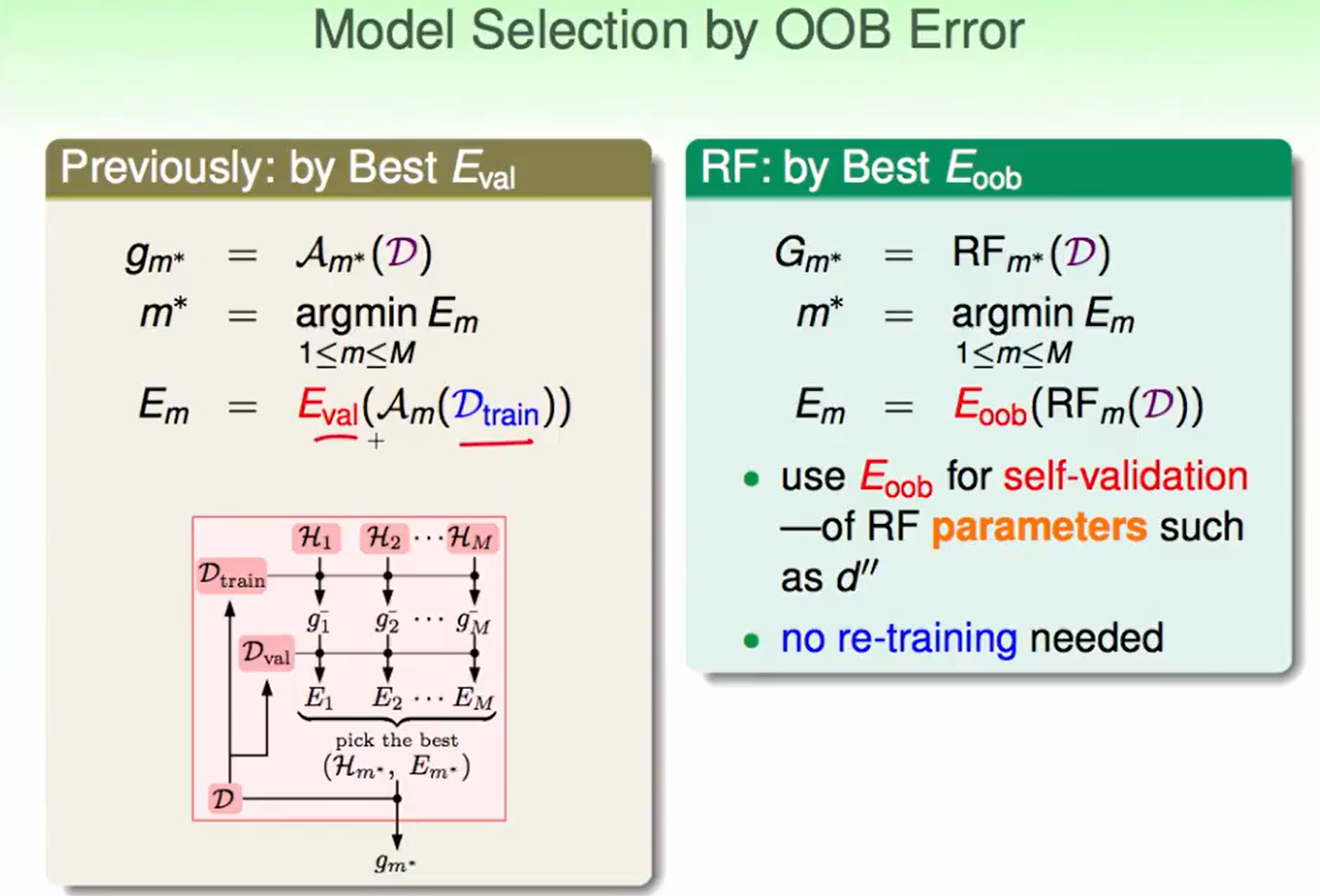
• 传统的用$E_{val}$来选择的方法，我们需要做两次训练动作，第一次用一部分训练$g$，然后validation选出最好的$g$，最后再用所有的数据重新训练这个hypothesis。

• 而$E_{oob}$只需要训练一次

Feature Selection

• 冗余的特征：例如生日和年龄
• 无关的特征：比如在预测癌症时，是否有保险这个东西和癌症没什么关系。

我们只需要一堆feature里的一个子集，这样高效且鲁棒性好。

虽然高效，但是你怎么选出这个子集呢？这是一个组合问题，这里确实很耗费时间的。

我们可以给每个feature打一个分，选择最高的几个即可，怎么定义这个分数呢？

这里介绍random test：

大致的思想就是：如果一个维度很重要，那我把这个维度污染后得到结果回合原来的结果差距就会很大。

怎么污染呢？可以用permutation test来污染，我们把这一个维度的数据洗牌(仅仅是这个维度)，然后和原来的表现做对比。

剩下最后一个问题，我们怎么衡量$performance$呢？

我们不想再用validation了，因为这样会重新训练一下才能得到结果，我们可以用$E_{oob}$代替。

Random Forest in Action

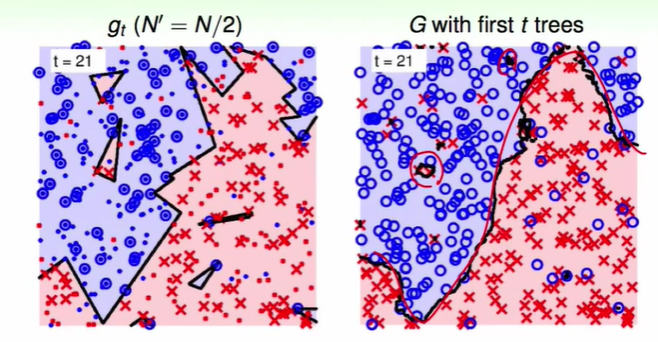
我们来做一个对比：

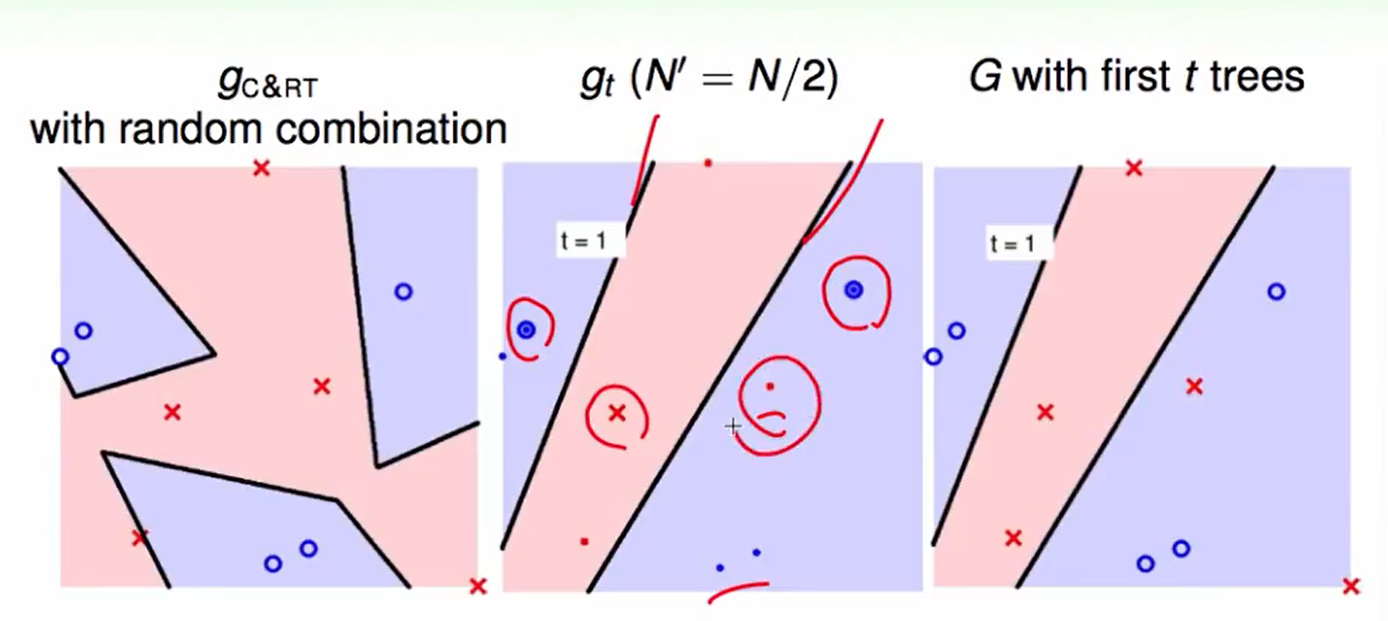
上图从左到右分别为：用C&RT with random combination做的结果，第 t 次bootstrap得到的$g_t$，$t$棵树合在一起的效果。

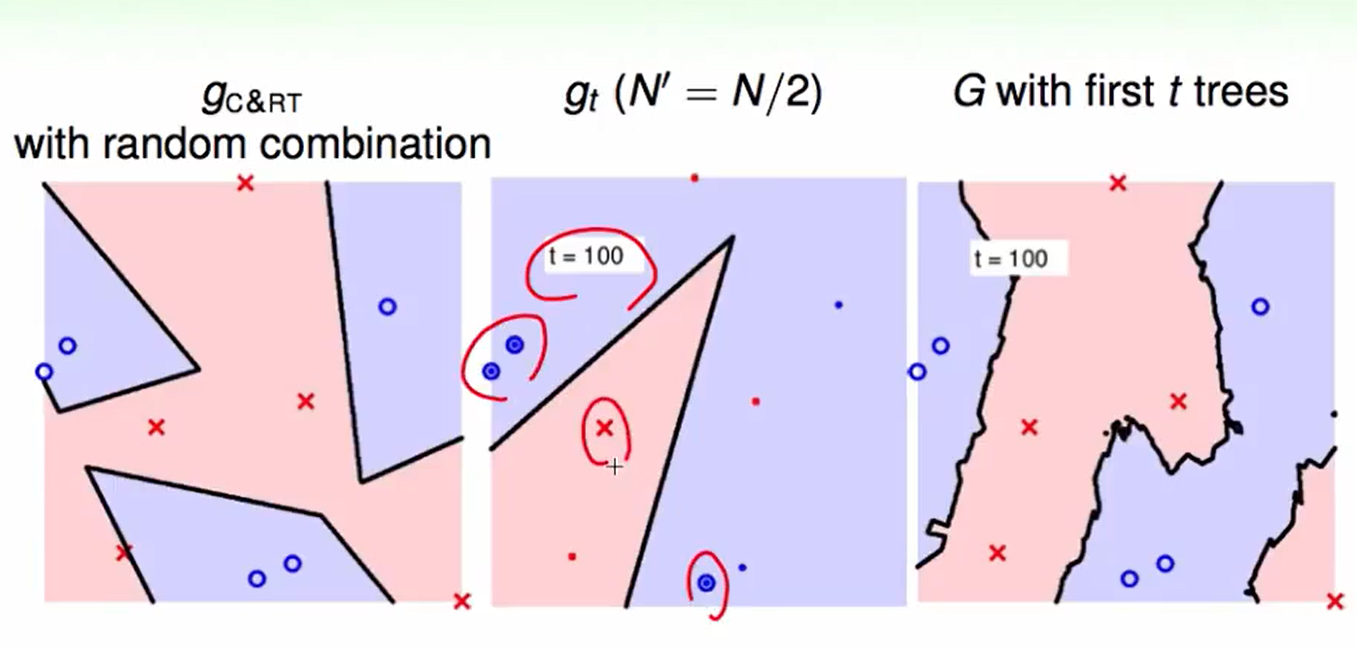
我们把迭代次数增加：

t=100

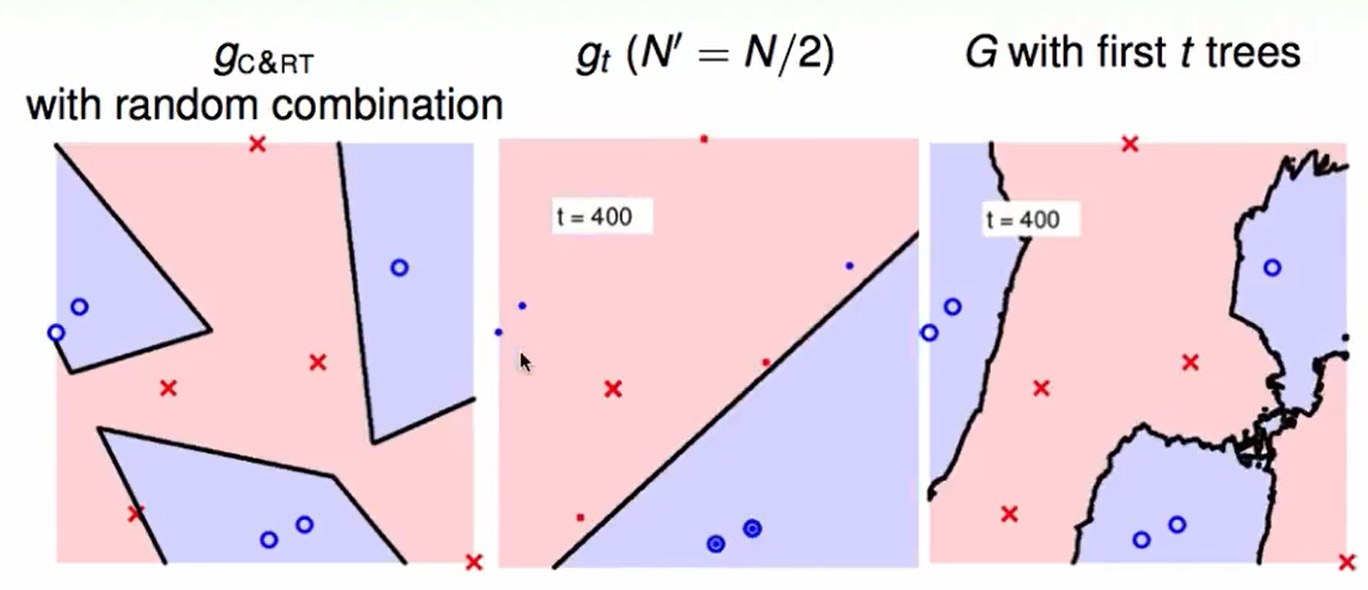
t=400

t=1000

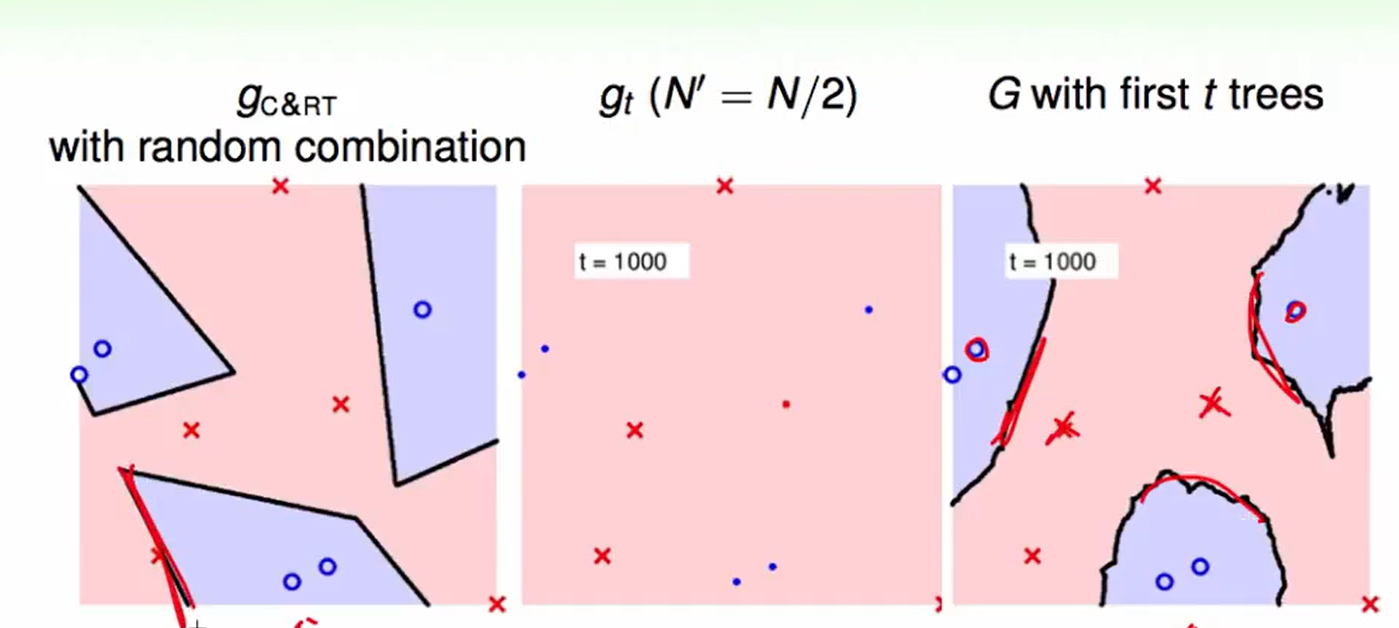
观察上图的左下角在边上的红色叉叉，如果是通过random forest来做，可以发现得到结果没有在边上，也就是做到了large-margin。

并且边界更加光滑。

我们对一份数据加上10%噪音

random forest依然得到了很好的效果.