CH11：Gradient Boosted Decision Tree

AdaBoost Decision Tree

我们在AdaBoost-DTree中的第二步的DTree算法中加入了权重$u^{(t)}$。

如何实现这个呢 ？

我们回想一下在bootstrap中，我们把$u_n$代表着每个数据被选到的数量。但是我们现在的DTree算法没有权重这一说，我们又想要加上权重这个概念，那怎么办呢？

我们可以提前先对数据处理一下，比如原来有三个数据(1,1)(2,2) (3,3),权重是2，1，0，也就是2个(1,1),1个(2,2),没有(3,3),那么我们把数据先改变为(1,1)(1,1)(2,2),然后再去随机抽取，这样就用 抽到的概率 代替了 权重的概念。

我们现在用sampling 来代替权重概念，还没有魔改DTree。

在AdaBoost中 $\alpha_t = ln(♦_t) = ln \sqrt{(1-\epsilon_t)/\epsilon_t}$,我们如果同样用到这里：

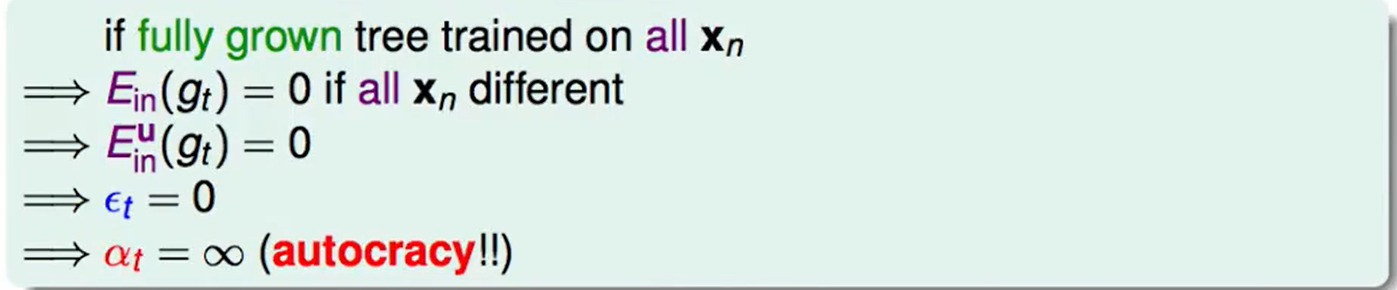
我们发现如果我们把树做成了fully-grown，那么$E_{in}=0$,那么会导致权重$\alpha = ∞$，这样就导致了只有这一个$g_t$来决定了，这不就变成decision tree了吗？

我们可以用一些手段来限制长成fully-grwon，并且尽量让他不全作对：

• 可以pruned来限制树高
• 我们抽一部分数据来训练decision tree。

我们反正不需要做的太好，我们把树高限制在1层就好了

一层不就是decision stump了吗？

我们称之为AdaBoost-Stump ，他就是AdaBoost-DTree的一种特殊情况。

此时也不用做sampling了，因为此时$E_{in}=0$的可能性几乎不存在了，做这个多此一举。

Optimization of AdaBoost

再来回顾一下AdaBoost中的权重迭代：

我们是否可以写成一个整体呢？即等两种形式都写成乘菱形的形式。

那么我们可以直接推出$u_n^{T+1}$的通项公式：

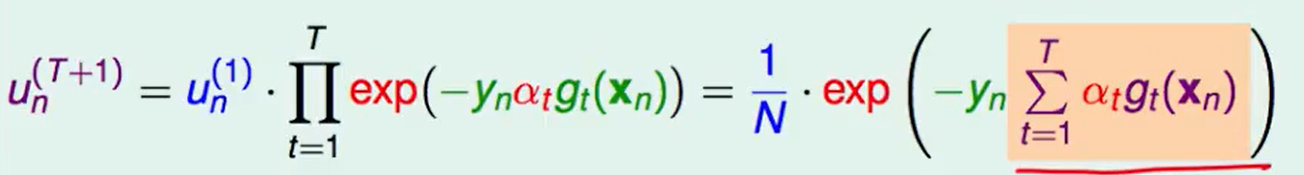
其中橘色的一项就是AdaBoost最终返回的结果$G(x)$：

在linear blending那一节提到过：linear blending和 线性模型+feature transform很像。(如下图)

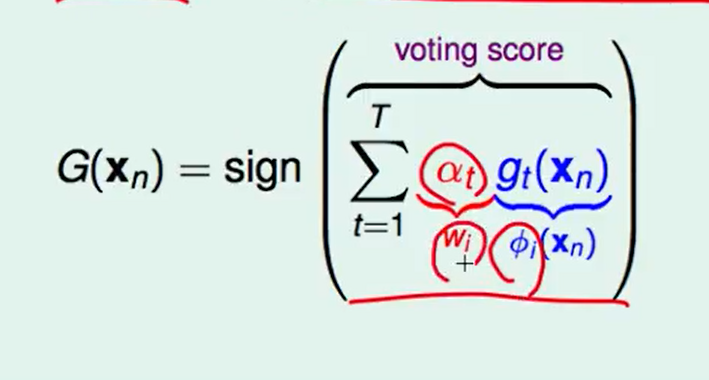
而hard-margin SVM margin的表达式是：

这里的$w^T\phi(x_n)$的就是还没有正规化之前的距离，$y_n$无所谓，他只代表在哪儿一边。

这么来看，margin和voting score好像很相似，至少表达了同一种性质。

所以当迭代的次数多一些，$u_n^{(T+1)}$小一些，AdaBoost可以达到large margin的效果。

$u_n^{(T+1)}$小一些，AdaBoost效果就好一点，那不如把$u_n^{(T+1)}$看作一种新的error measure的指标。

且这种新的错误指标还是0/1 error measure的上界，那我们能做到很好吗？

我们来证明一下：

首先回顾gradient descent：

$\eta$是步长/学习率，$v^T$是梯度的反方向。

同理我们考虑$Min\ E_{ADA}$是否也可以转化成这种想法：

在第$t$次迭代，我们想找一个$h$使得error迭代后最小。

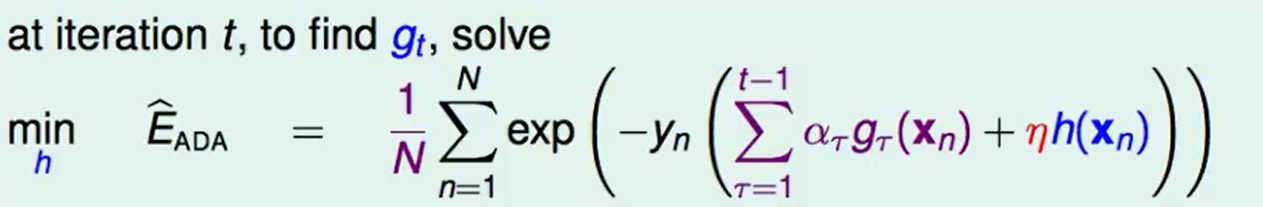
化简：

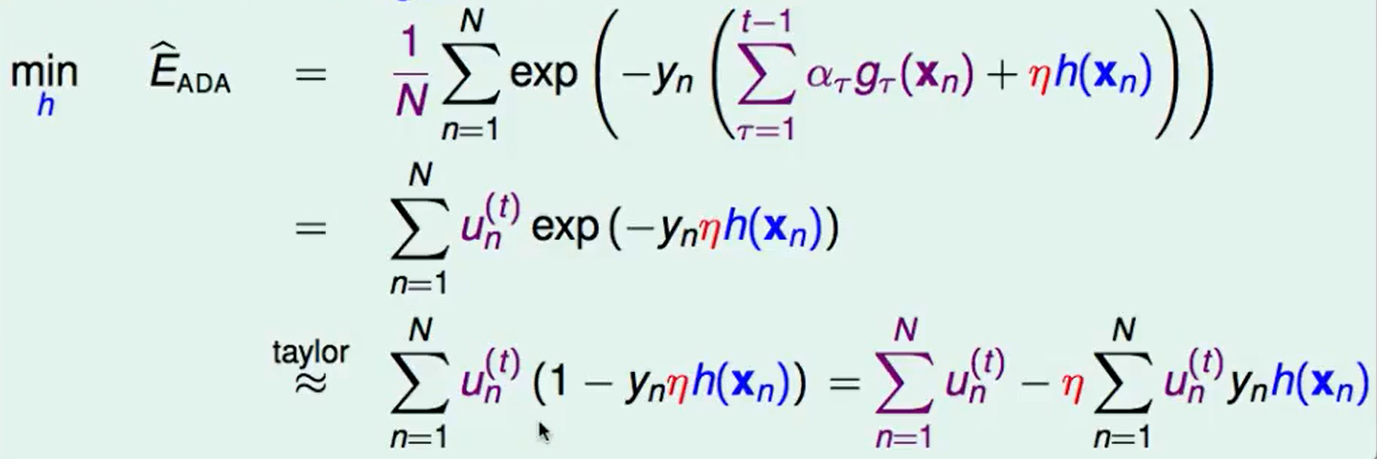
现在问题转化为了：如何最小化第二项。

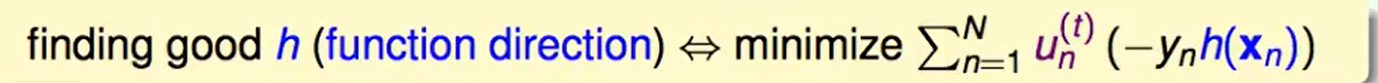
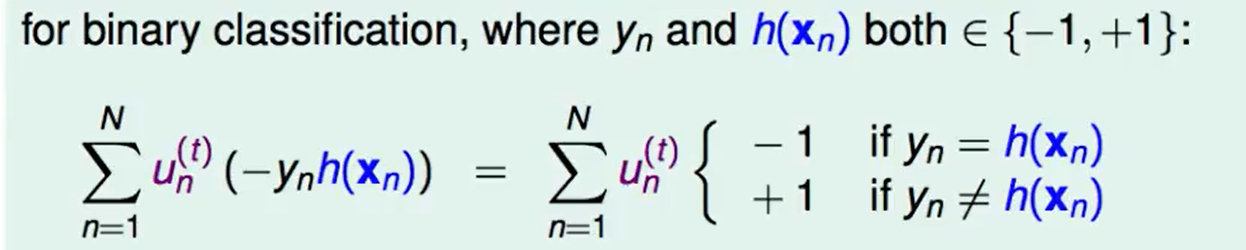
我们现在把这个式子做一个平移：

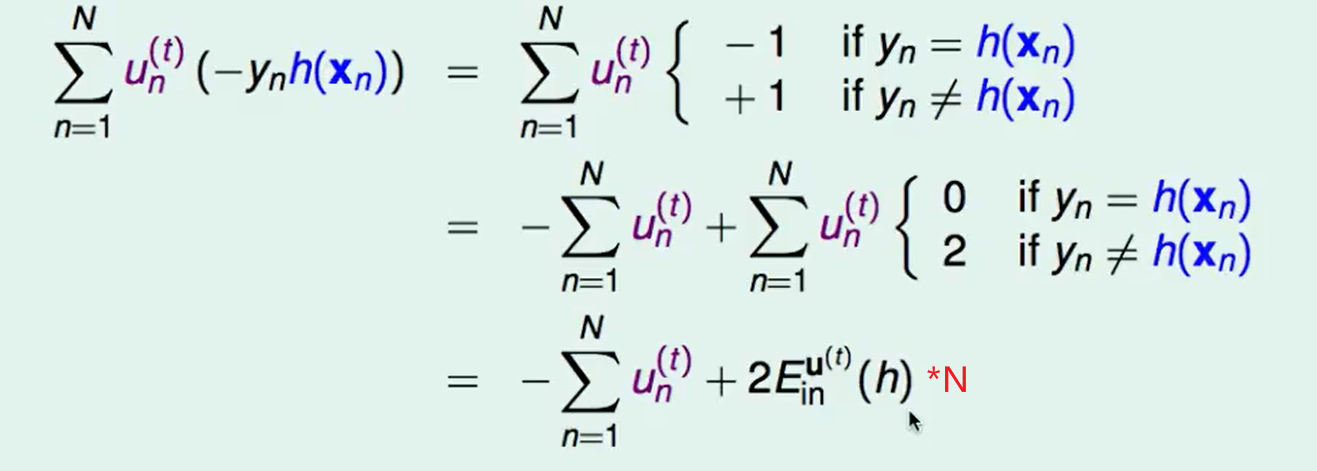
那么我们最小化$E_{in}^{u(t)}(h)$即可

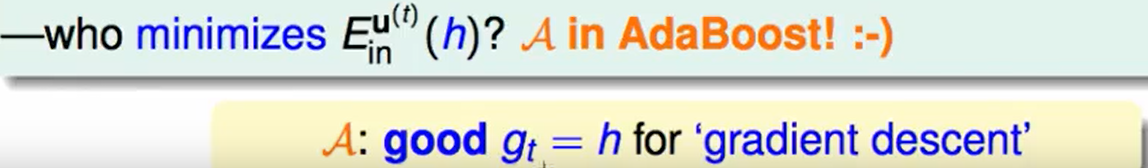
那么谁在最小化$E_{in}^{u(t)}(h)$？ 这个问题等价于：谁找到了一个最好的$h$作为$g_t$?

我们看下AdaBoost的算法流程：

很明显最小化$E_{in}^{u(t)}(h)$的任务就是AdaBoost算法中的$A$来做的，而且这个最好的$h$就像是梯度下降中的梯度方向。

我们找到最好的h，也就是$g_t$后，我们想着走的大步一些：

这样找的最优的$\eta$由于是贪心的来走，所以肯定比一个固定的$\eta$大：

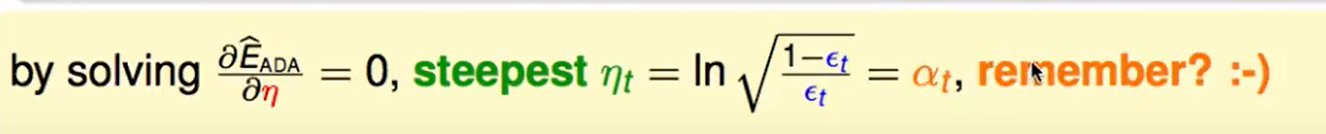
我缓缓打出一个问号？ 这个最好的$\eta$居然就是$\alpha_t$。

之前我们认为$\alpha_t$是在帮我们做不同$g_t$权重的衡量,现在来看，背后还在帮助我们做最佳化，快速到达最好的局面。

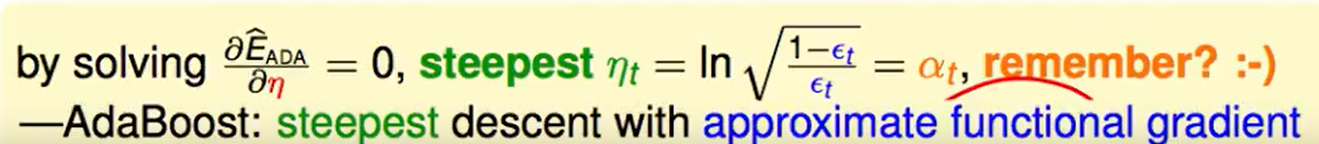
AdaBoost中的这种steepest decent用到了函数式梯度。

Gradient Boosting

那么AdaBoost的本质是：

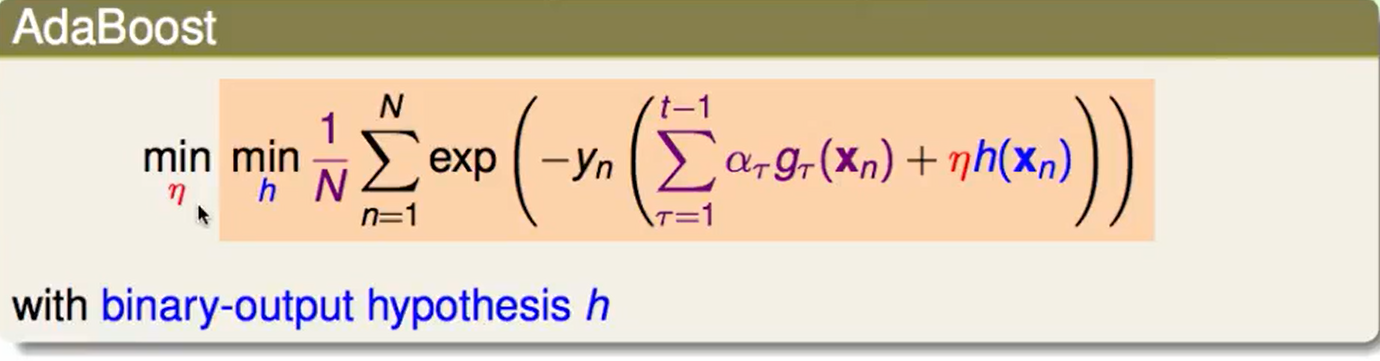
我们可以把这种思想带入任何其他的error measure方法：

这种算法就是GradientBoost。

由于任何error measure都可以使用，那么：

我们现在对回归任务/软分类问题也做GradientBoost。

我们下面再回归任务上来看看GradientBoost怎么用的：

和上一节AdaBoost一样，做Taylor展开：

$h(x)$是走的方向，那么他应该要和$2(s_n-y_n)$组合起来保持是负的，才能不断地是原算式边小。

那么$h(x)$符号方面至少要保证$h(x_n) = -k*(s_n-y_n),其中k>0$,我们希望下降的越大越好，反正$h$没什么限制，不妨让$k$趋于无穷

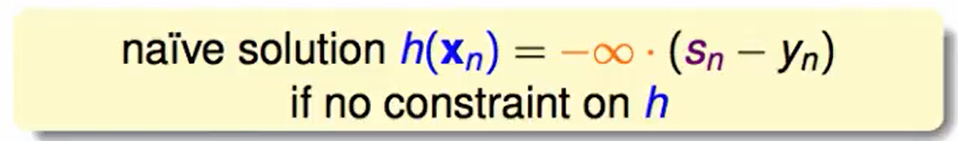
这么做看起来明显不是很合理，之前再gradient descent中我们限制了梯度向量的长度为一个定值。

那么谁来解决$h(x_n)$的大小问题呢？用$\eta$，因为$\eta$是第二层，外面那一层的优化，他会帮我们来做这个事情。

我们首先加上了一个平方项，这个和最小化式子是相违背的，这样就帮助我们尽可能地减小$h(x)_n$的大小。

我们并不关注那些常数项，和最优化没关系。

最后我们推出我们只关心$h(x_n)$和$(y_n-s_n)$的相似度，而$(y_n-s_n)$代表了实际与预期的差距。

那么现在的我们最小化的就是 这样一个square error：$(h(x_n)-(y_n-s_n))^2$,再做对数据${(x_n,y_n-s_n)}$一次regression找最好的$h$即可。

现在问题转化为了：

发现又变成了squre error的形式，等于现在再做一次regression，不过我们的只求一个$\eta$。

最后把所有的东西合并在一起，提出Gradient Boosted Decision Tree(GBDT)算法

Gradient Boosted Decision Tree(GBDT)：

Summary of Aggregation

首先是blending(即已经获得$g_t$后的aggregate方法)

• uniform：适用于$g_t$的地位相差不大

• non-uniform：也就是linear blending，要小心overfit

• conditional：也就是stacking，要小心overfit

和第一种aggregation不同，这第二部分的aggregation是边学边获得$g_t$

• bagging：bootstrap抽取数据训练 + uniform合在一起

• AdaBoost：处理$g_t$的线性组合

• Decision Tree：处理conditional vote

还有一个GradientBoost，他的$g_t$的多样性通过对余数做regression来得到。

我们还可以进行组合：

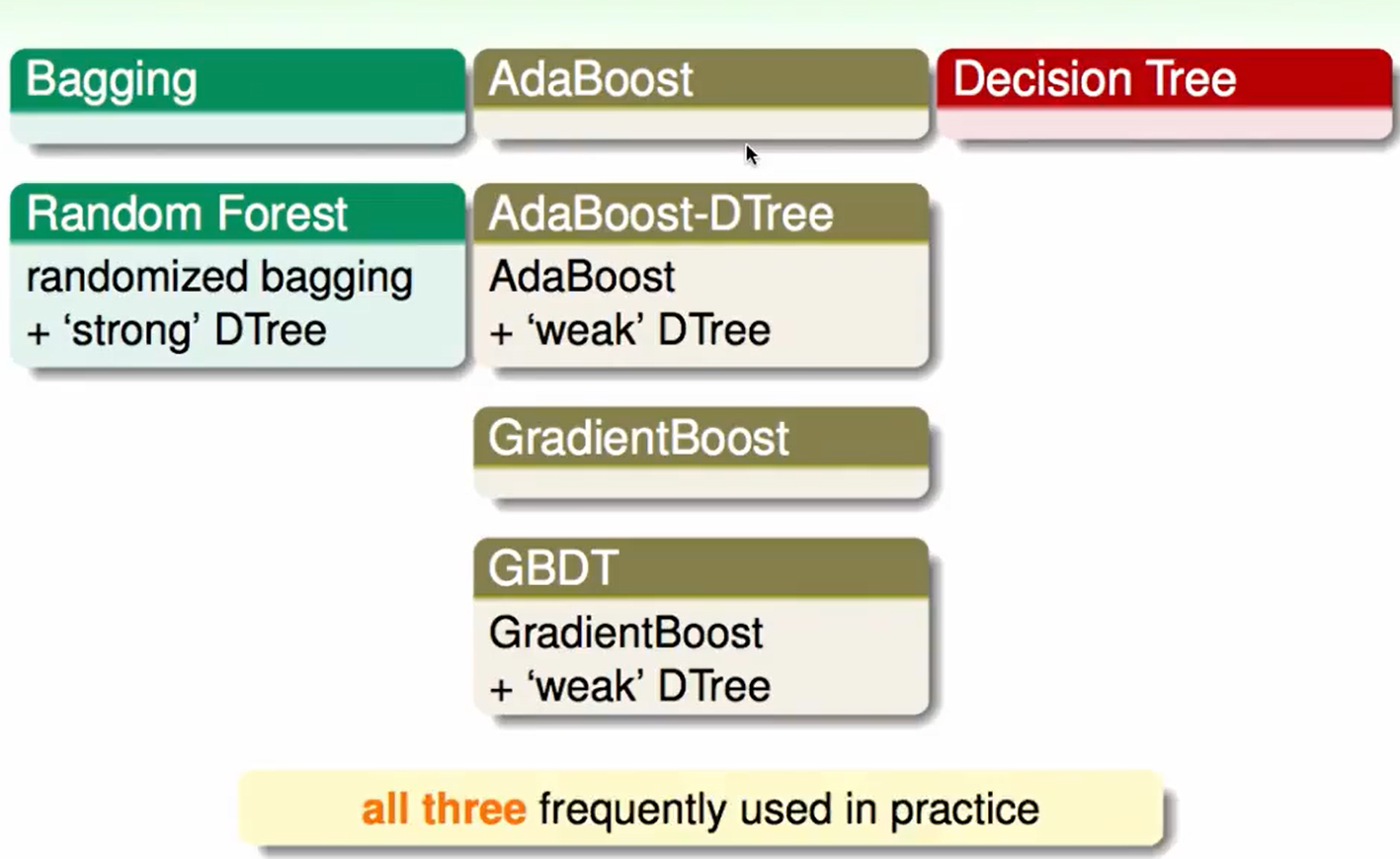
aggregation带来的好处是：

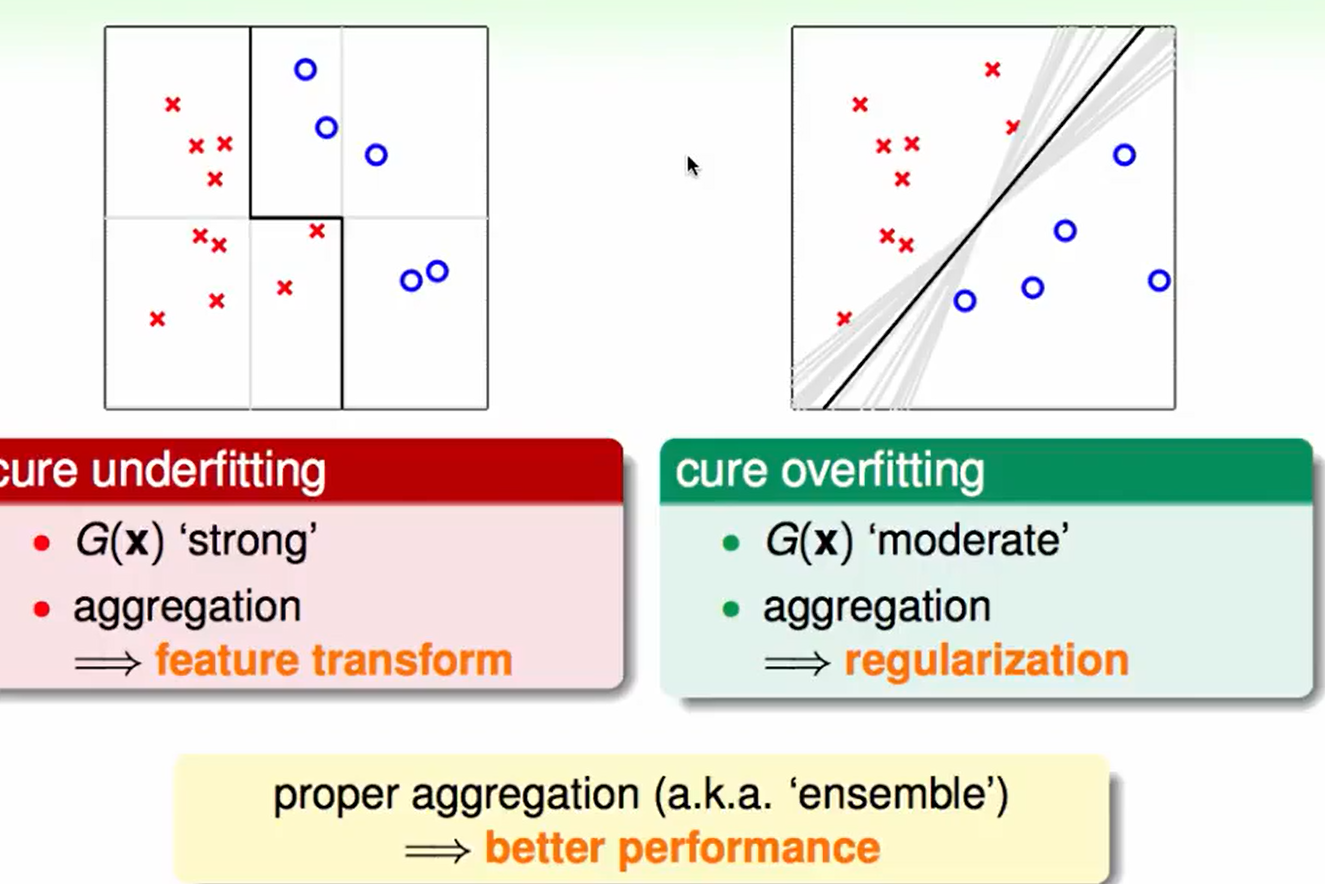
不拟合的时候aggregation相当于做feature transform帮你拟合，却也可以帮你regularization防止过拟合，因此选择合适的aggregation方法才可以获得更好的表现。