CH12：Neural Network

Motivation

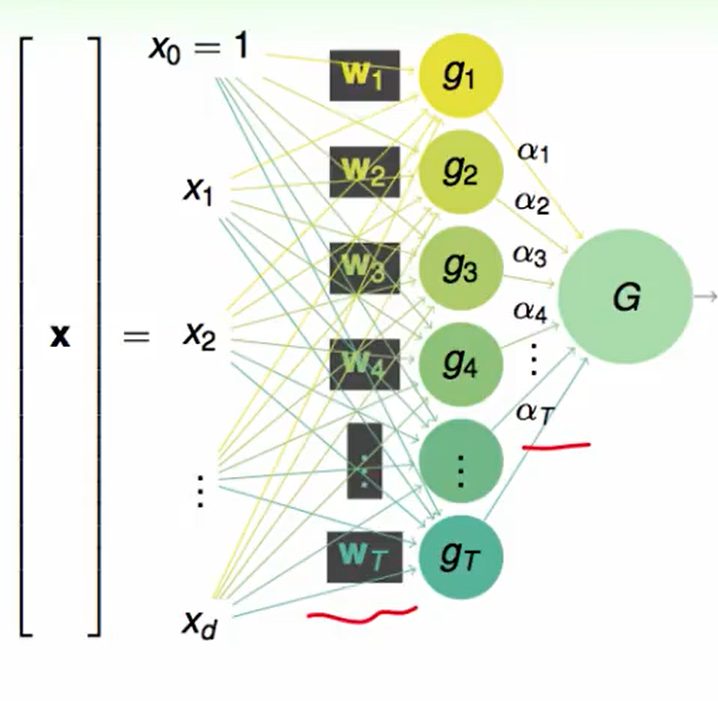
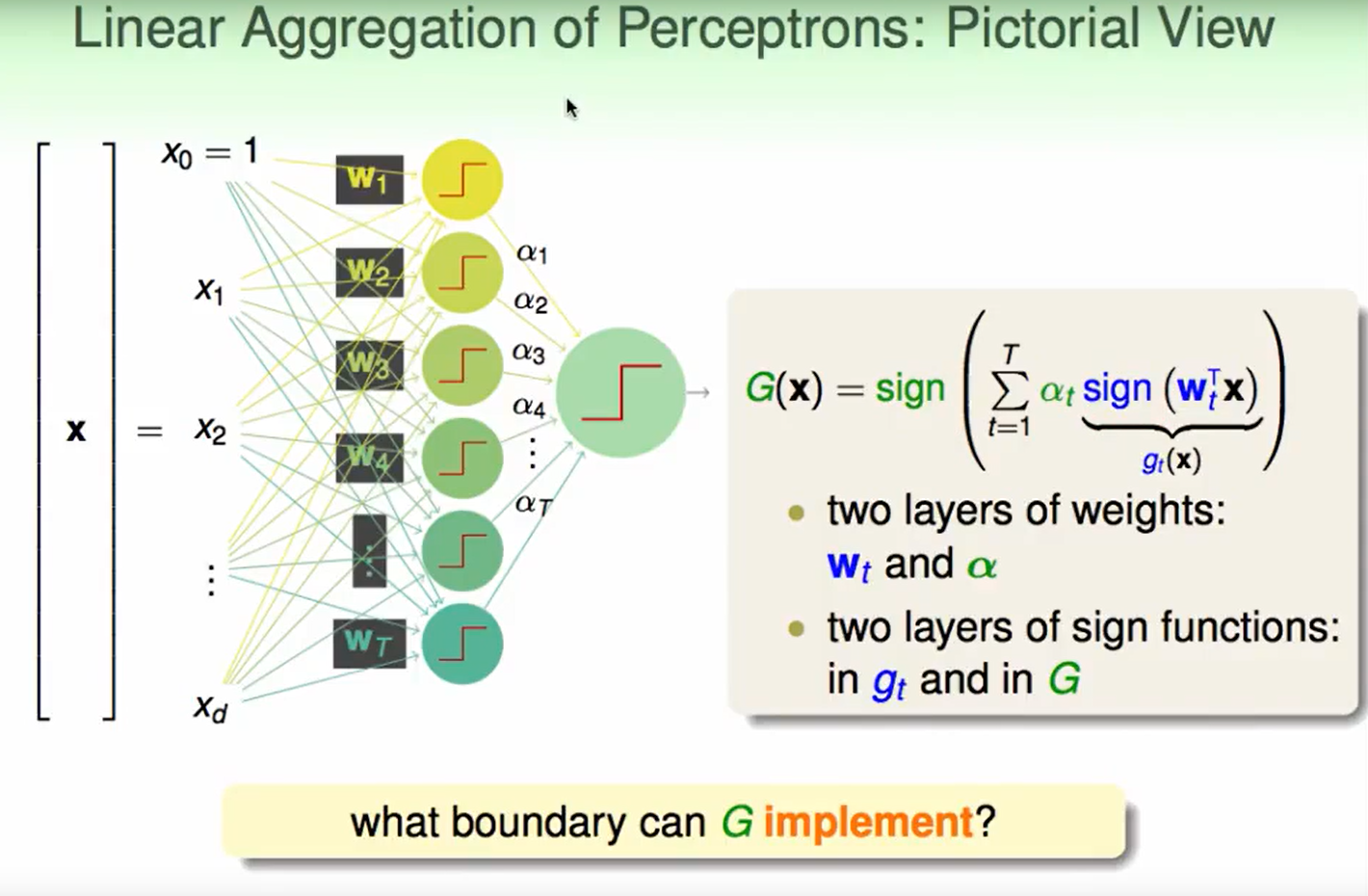
我们可以自由决定$w$和$\alpha$ .

首先这种aggregation操作可以做到logic operation(逻辑运算)：

AND运算：

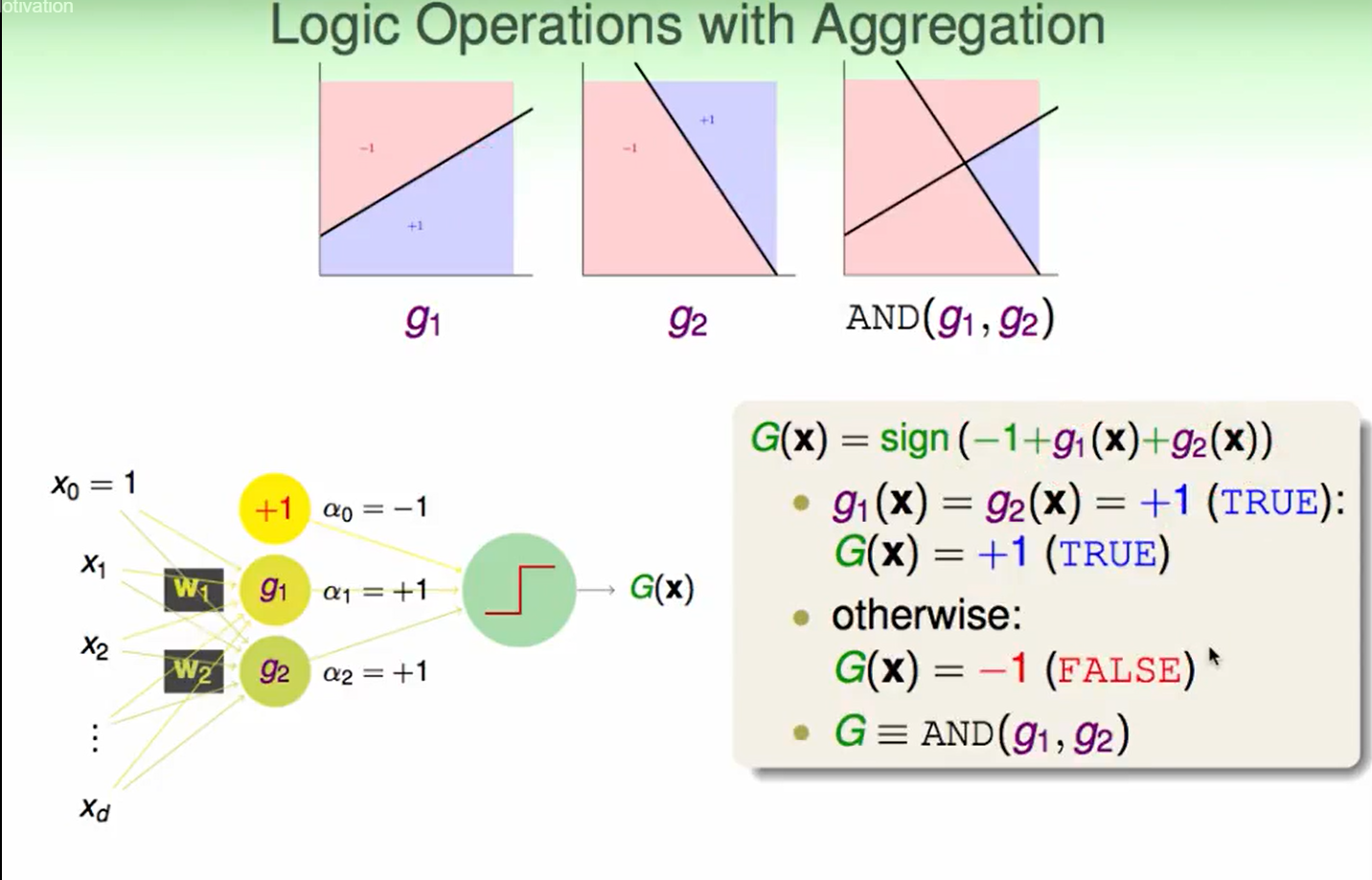
我们的这种aggregation of Perceptron是很复杂度 ：

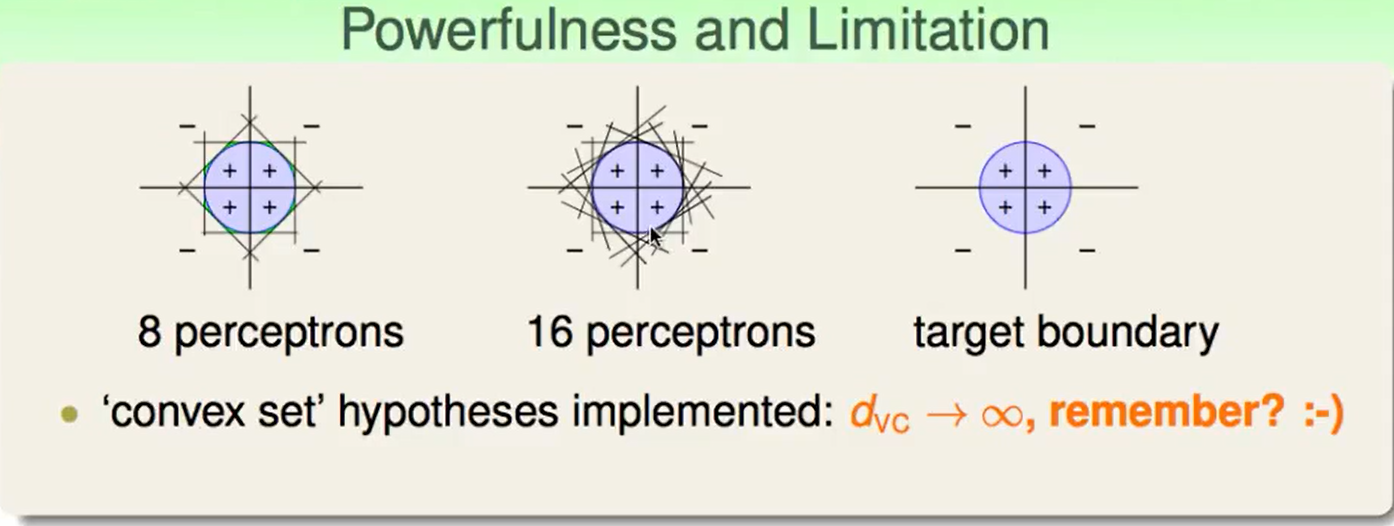
上图发现，我们用足够多的perceptron就可以得到一个近似于target boundary的结果，因此它是一种能力很强的组合方法。当然这也意味着很容易overfit。

当然这种方法也有一些局限(Limitation)：

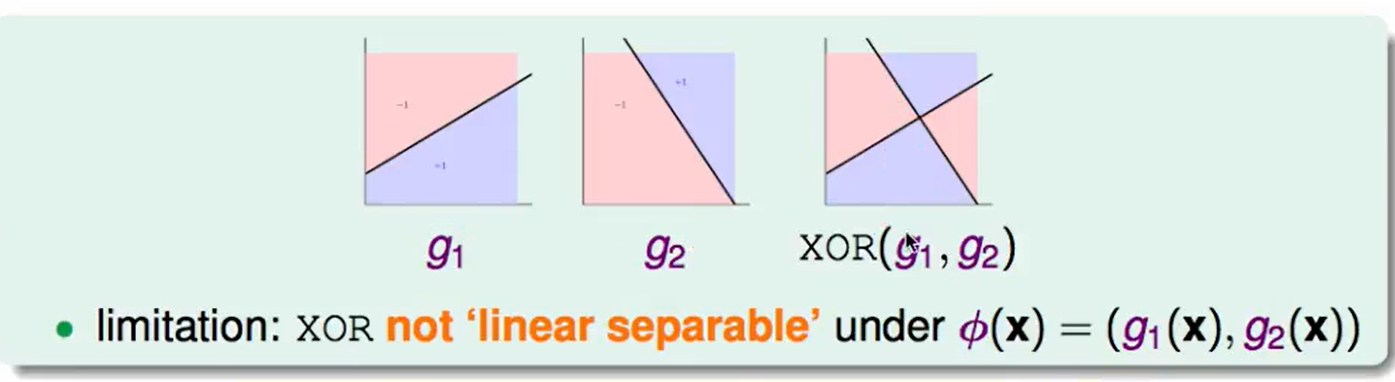
由于异或是非线性可分的，因此这种方法不能直接处理。

那可以先考虑做一次feature transform，那么也就是我要做两层转换。

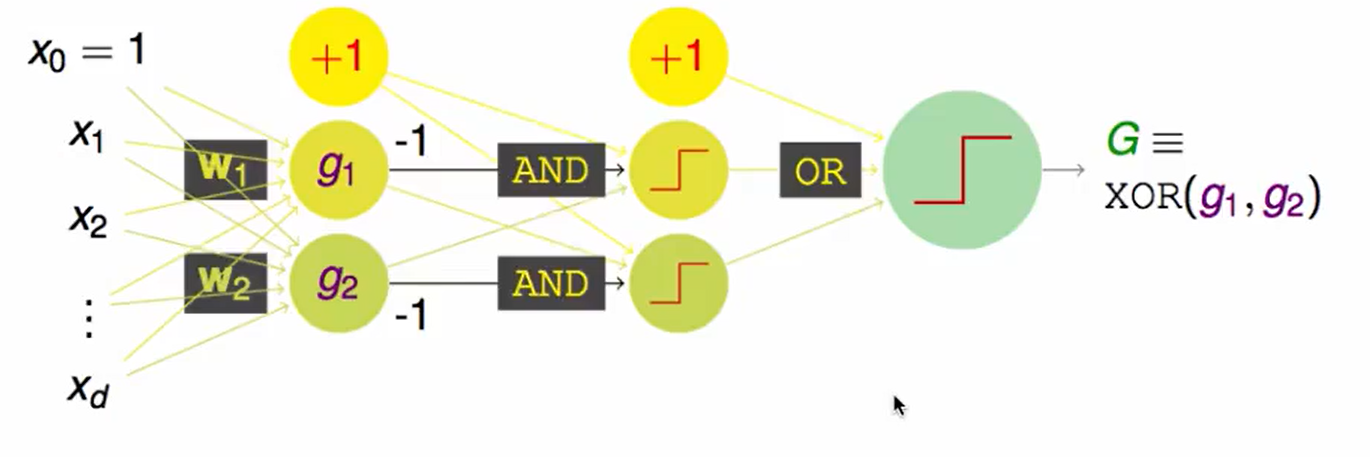
多层的perceptron就是basic Neural Network。

Neural Network Hypothesis

输出可以看作一个多层模型嵌套后的线性组合：$s=w^T\phi^{(1)}(\phi^{(2)}(\phi^{(3)}(…)))$

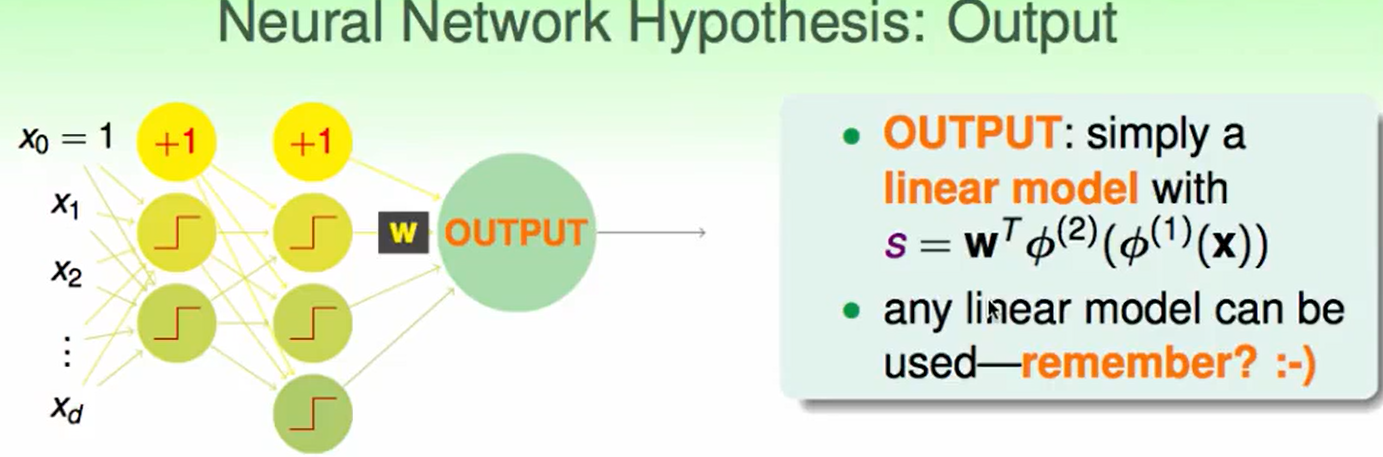
s可以做下面这三种操作：

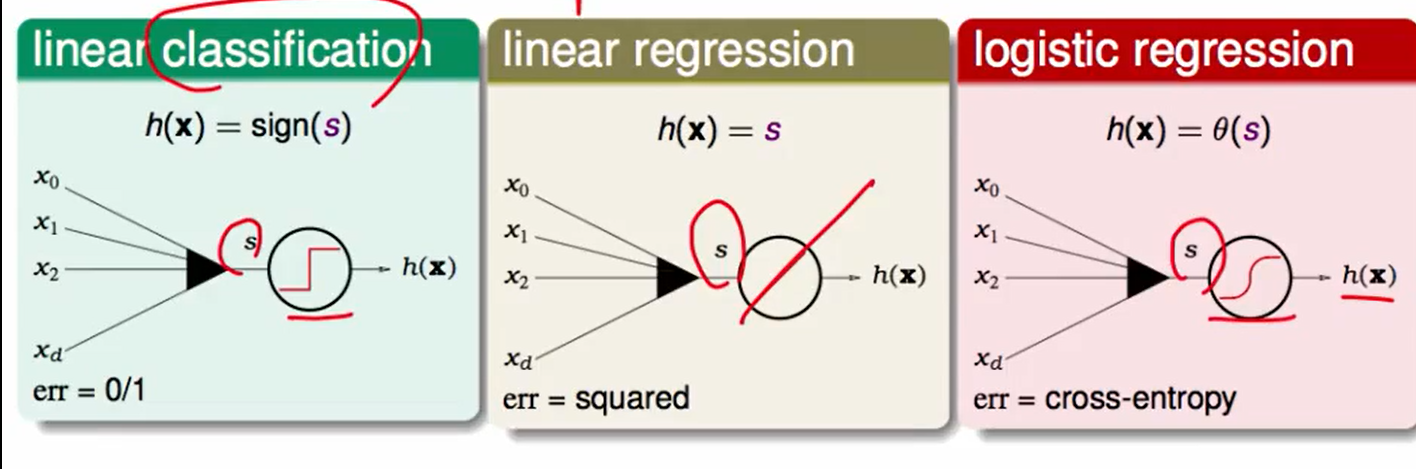
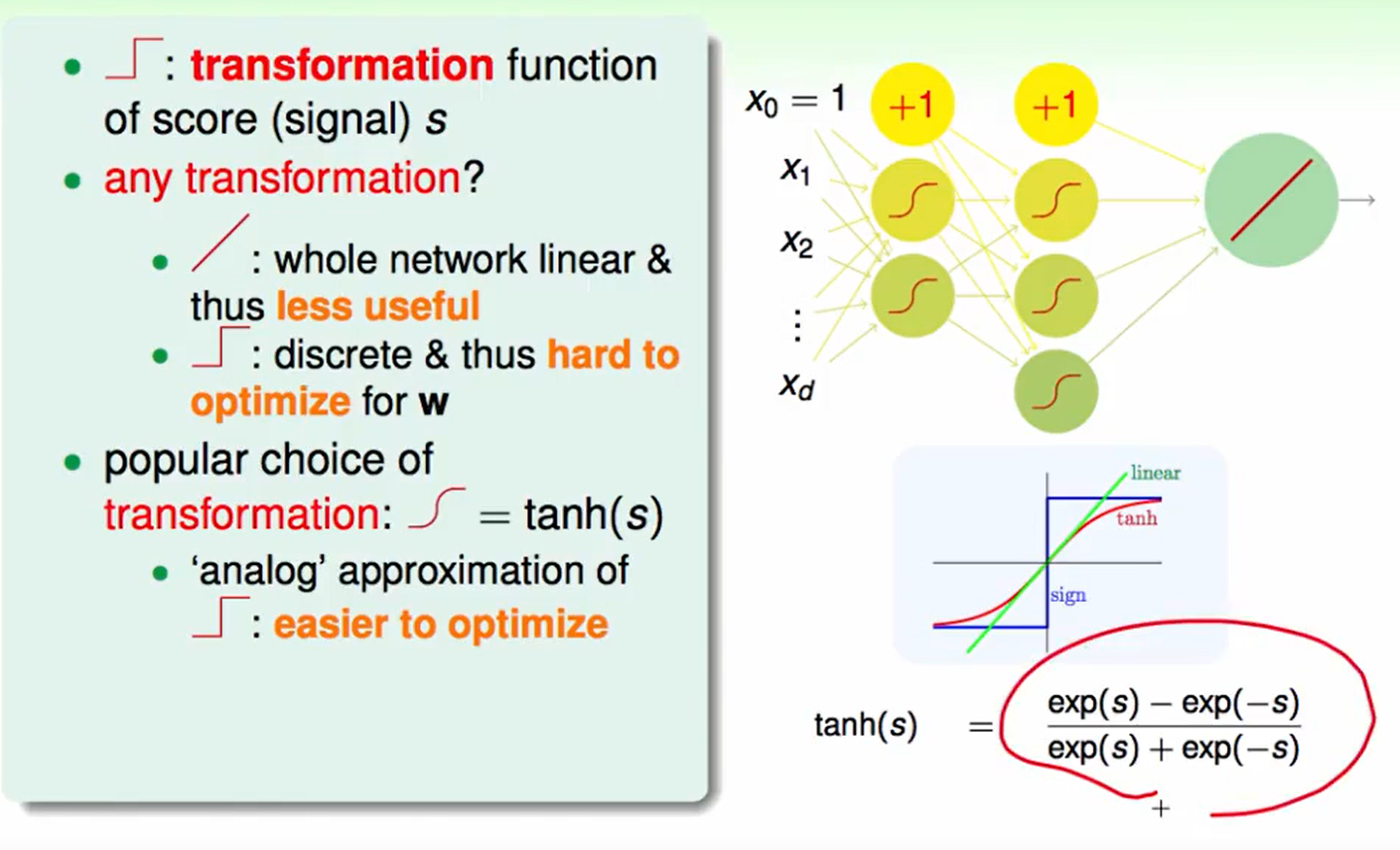
我们之前一直都讨论的神经元处理都是sign阶梯函数来处理的，但是这种很难最优化$w$,而若全部换成线性的，其实也没什么作用，因为线性的组合还是线性的，这样做是没有意义的。

因此考虑$tanh(s)$这个函数来处理，他在近似原点的地方符合linear，远离原点的地方符合sign.

同时注意到,$tanh(s)$可以化简为：$tanh(s) = 2\theta(2s)-1$

那么把这个hypothesis改进后:

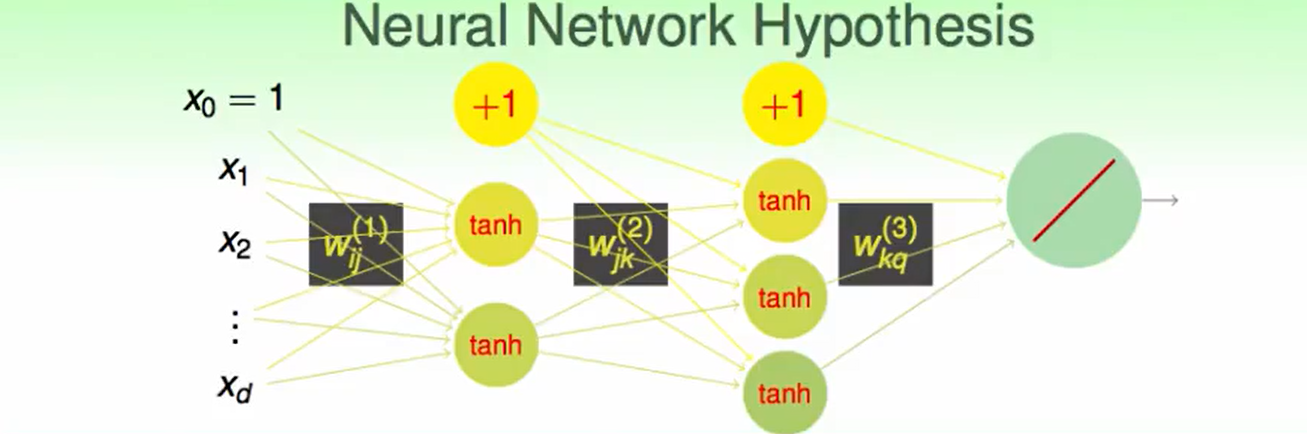
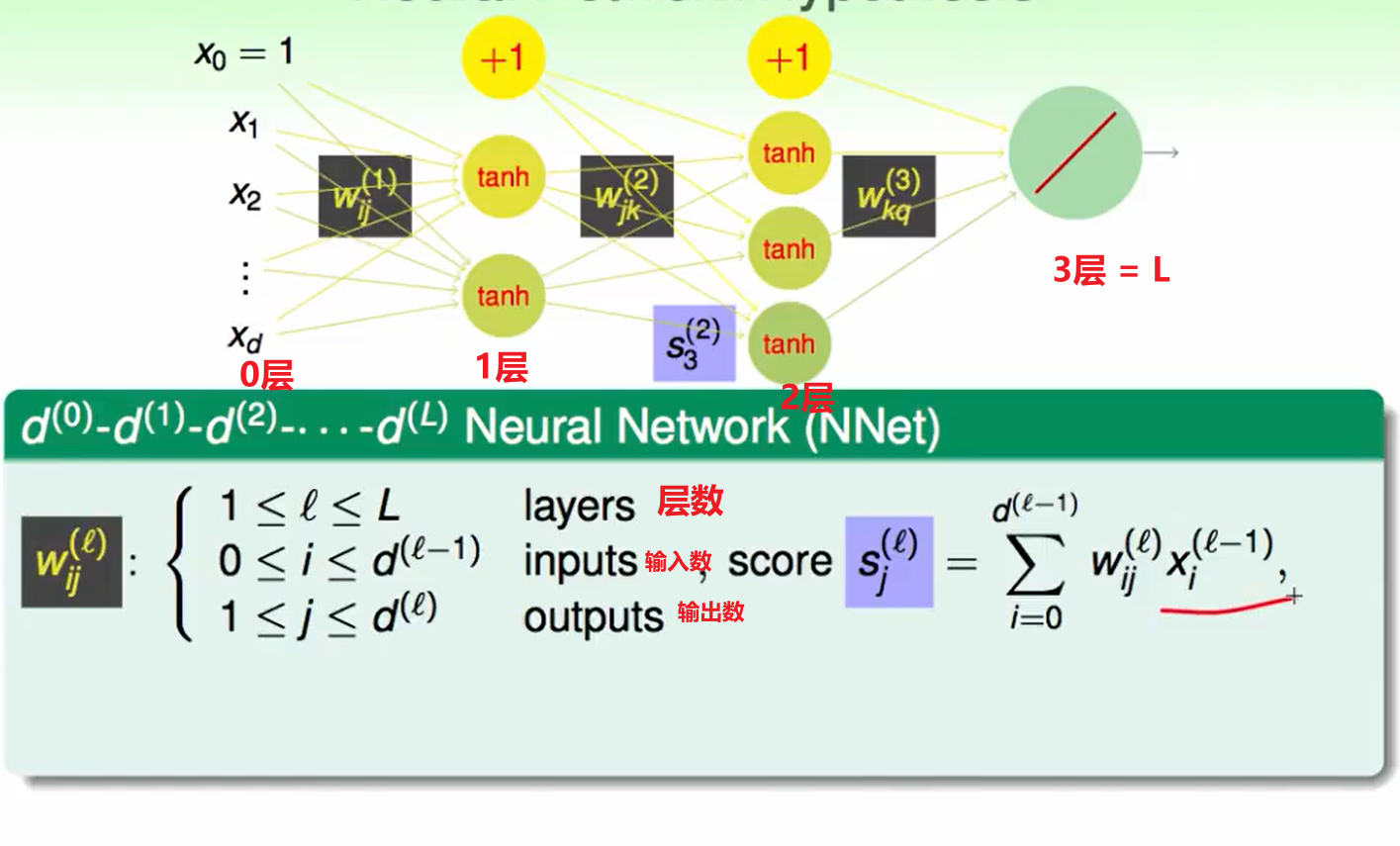
其中输入得第0号是输入的常数项。

我们提出了两个概念：一个是分数score，另一个是transformed转换后的输入：

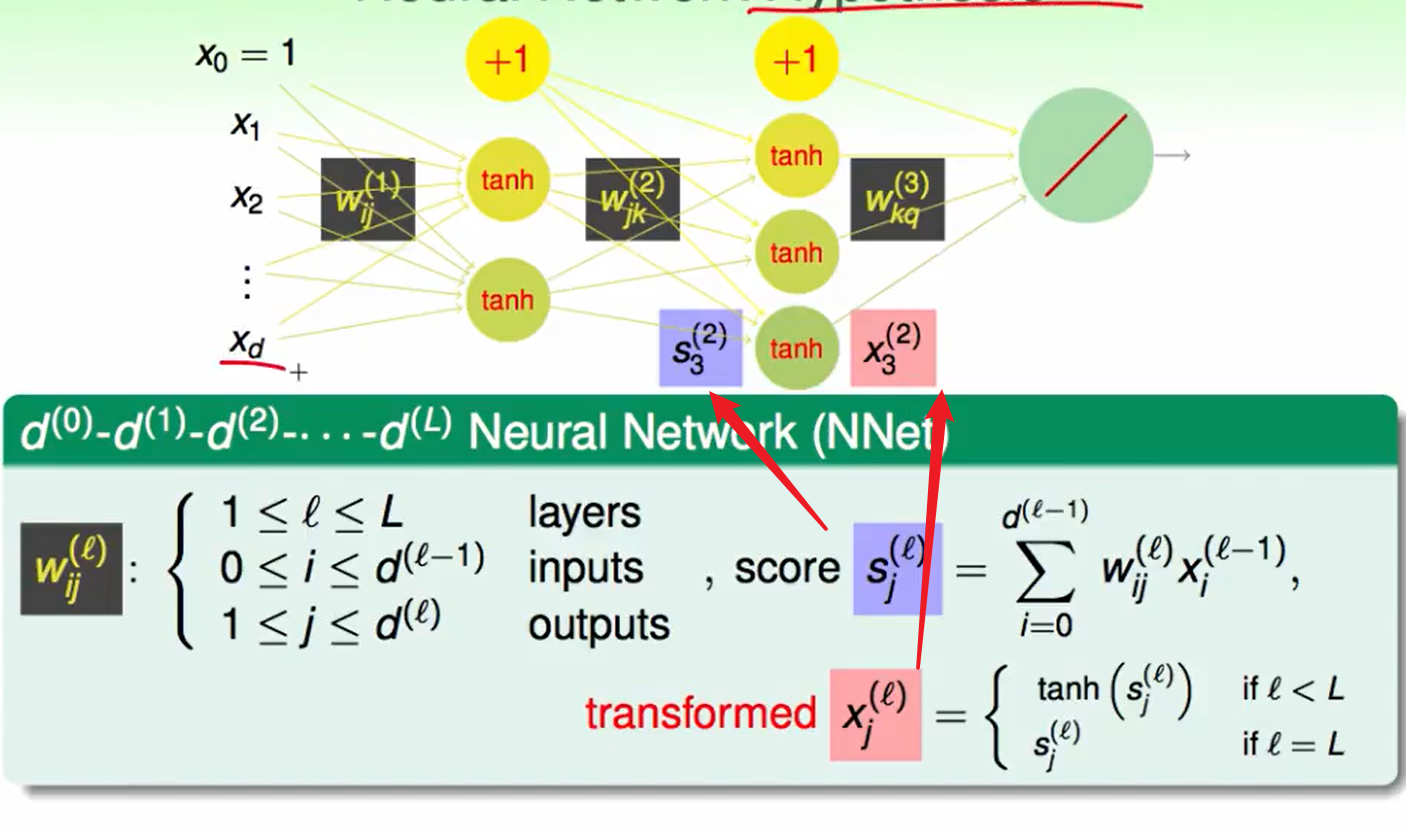
Neural Work Learning

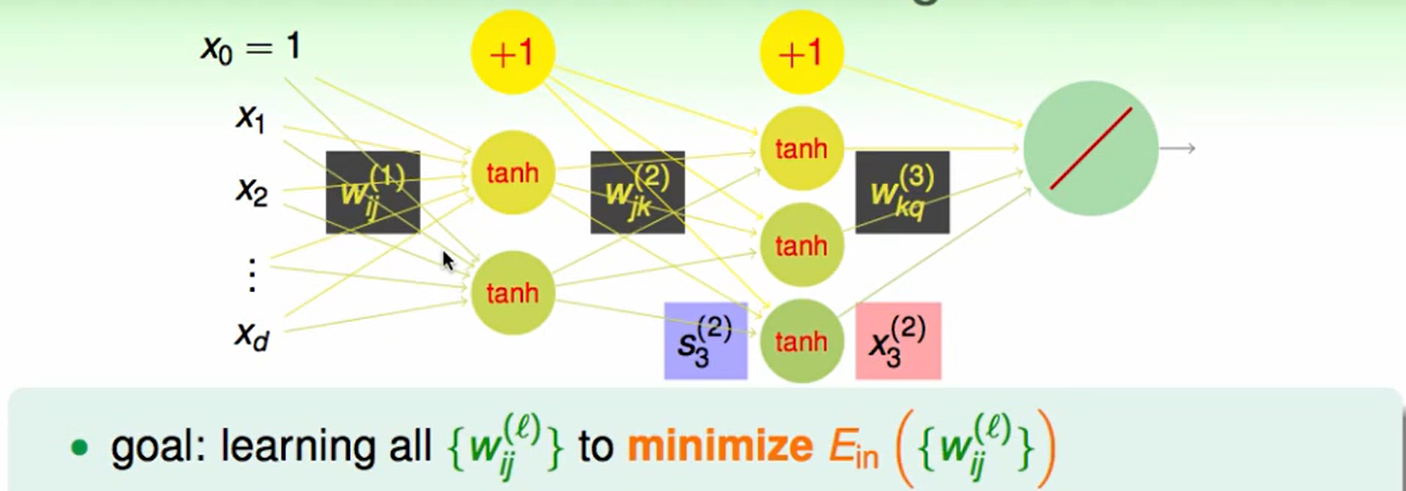
我们可以写成square error的形式：

但是这样的效率很低，因此目标是:

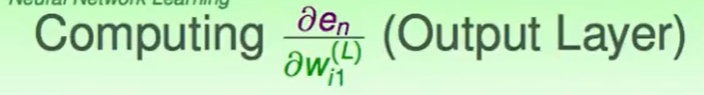
我们首先来算最后一层的，即第$L$层。

最后一层的输出是1的，那么$w^{(L)}$的应该是一个大小为$d^{(L-1)}*1$的矩阵：

那么最后一层可以很方便的算出来。

如果不是最后一层呢？

同样的方法我们应用到这里，但是对于$ \frac{\part e_n}{\part s_j^{(l)}}$，我们很难计算,因此我们选择用暂时不处理，并用$\delta_j^{(l)}$代替。

下面我们来处理这个难搞的偏微分：

一个$e_n$是$s_j^{(l)}$经多次变化才会得到的，如图：

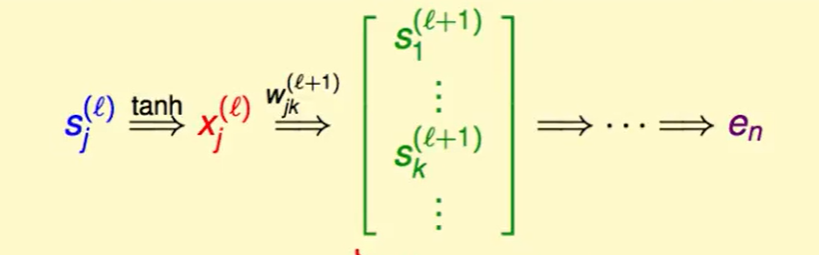
和之前一样，我们用连锁律来一步一步倒推回去：

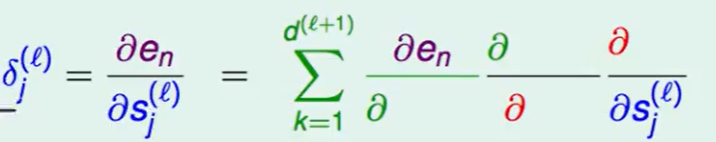
这里有个$\Sigma$的原因是因为$s$是一个高维的的数据,所以我们需要对 每一个都求偏微分加在一起。

最后写出下式：

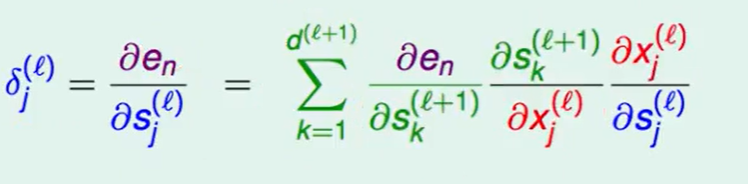
继续推到，第一项绿色的就是我们定义的$\delta$ ，红色项推导：根据上面的转换图可以看出$sk^{(l+1)}$是由$x_j^{(l)}*w{jk}^{(l+1)}$得到，故对偏微分就是$w_{jk}^{(l+1)}$.

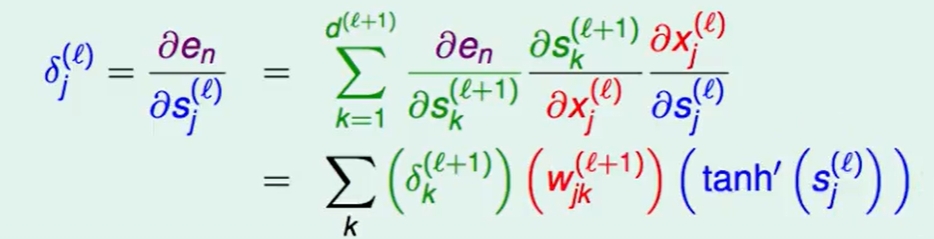
现在我们有了递推式$l$层可以通过$l+1$层推出。

那么我们就可以提出这个新的算法Backpropagation Algorithm反向传播算法：

实际应用中 ，对于一次运算④，我们回把①到③做多次去求得一个平均值，即$average(xi^{(l-1)}\delta{j}^{(l)})$。同时注意到这种①到③运算是可以并行的运算的，这就是大大加快了效率。

我们称这种多次运算取平均的方法叫做mini-batch

Optimization and Regularization

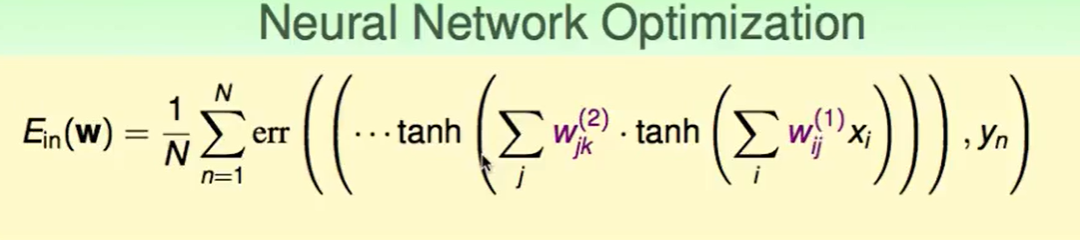
我们写出$E_{in}$函数，发现下面这几个问题：

第一，这个是一个非凸的函数，因此会有很多个山谷，因此我们并不是很容易中找到一个全局最小化的地方，我们所用的GD/SGD 通过反向传播算法得到的也只是一个局部的最小值。

第二，由于有多个山谷，权重$w$的不同初始化的值会导致不同的局部最小值，坦白来说，并没有什么最好的方法来最优的初始化这个$w$,但是我们可以通过一些技巧来做到一个还算不错的结果。

• 首先如果权重$w$很大,那么做$tanh()$时会导致梯度非常小，为什么呢？$tanh()$在$w$非常大的时候函数曲线已经接近平的了，这样我们每次只会走非常小的一步，这样就在有限的次数里可能不会走到最小的谷底。
• 因此给出的建议是：权重选择要随机一些，同时权重尽量一些。

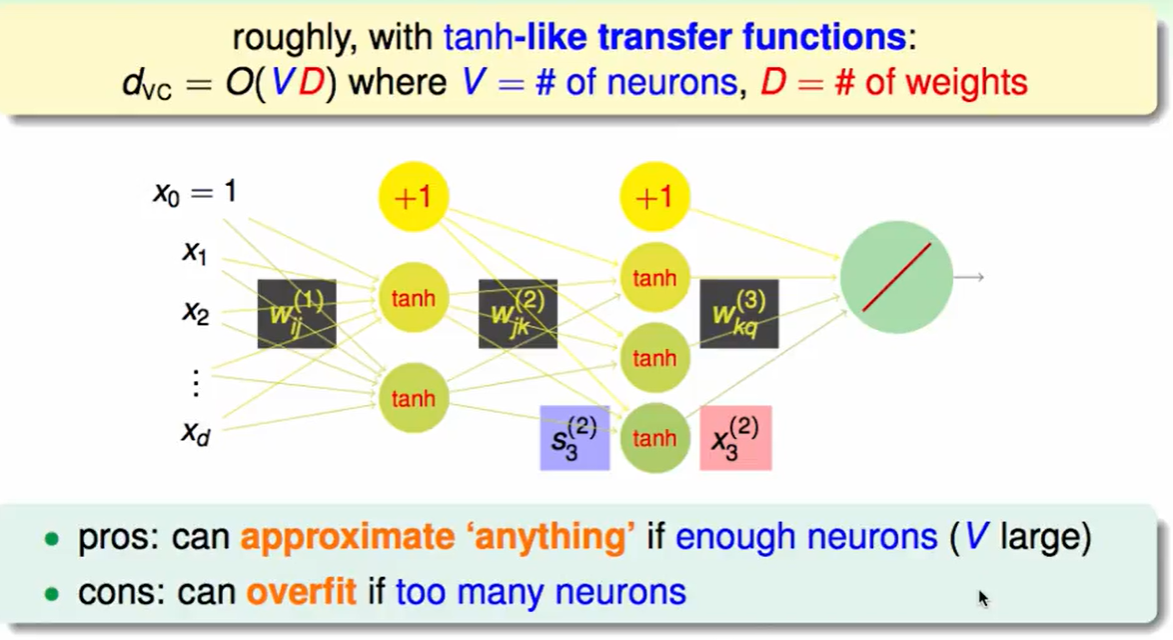
那么这个算法在使用tanh做transfer function的情况下的复杂度，用VC dimension来衡量大概是$O(VD)$。 他可以来做许多事情如果你的神经元足够多。但是同样也要小心这样带来的overfitting。

对于overfitting，我们可以做Regularization:

我们不难想到一种basic choice就是 做L2正则化，限制w的权重平方和。

但是这么做没什么意义，好比一个近似等比例的缩小：

比如原来的权重是8现在就是4，原来是10现在就是6，这种放缩并不会帮助你解绝overfit。

L2正则化本质上没有帮我们解决降低$d_{VC}$的问题，也就是说没有帮我们把一些w变成0.

我们现在不妨考虑L1正则化：

但是这有一些问题，就是带着绝对值不好微分，backprop是要求微分的。

还有一种比较常用的方法就是使用weight-elimination regularizer。weight-elimination regularizer类似于L2 regularizer，只不过是在L2 regularizer上做了尺度的缩小，这样能使large weight和small weight都能得到同等程度的缩小，从而让更多权重最终为零。weight-elimination regularizer的表达式如下：

还有一种有趣的正则化方法：early stopping

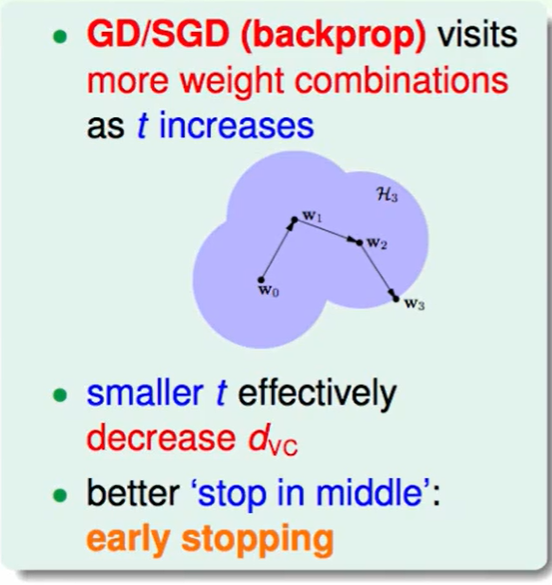
我们每次的GD只是观察一个小的范围内并作出选择，随着我们迭代次数变多，也就是时间变长，我们看到的会更多也就会导致overfit，因此我们运行的时间越短，那么$d_{VC}$也会越小。

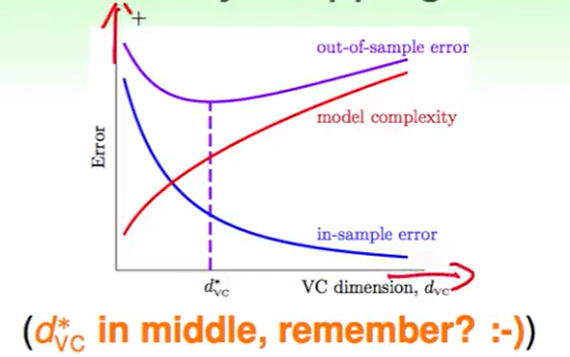
因此我们选一个适合的时间，得到一个适合的$d_{VC}$,那么我们就可以获得一个不错的结果。

下面是一个运行时间t和错误率 的关系的图：

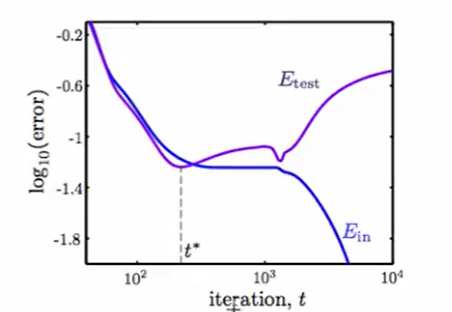
那么也就是说我们还要选择一个参数：时间$t$

怎么做呢？ Validation！