机器学习技法CH13:Deep Learning
CH13:Deep Learning
Deep Neural Network
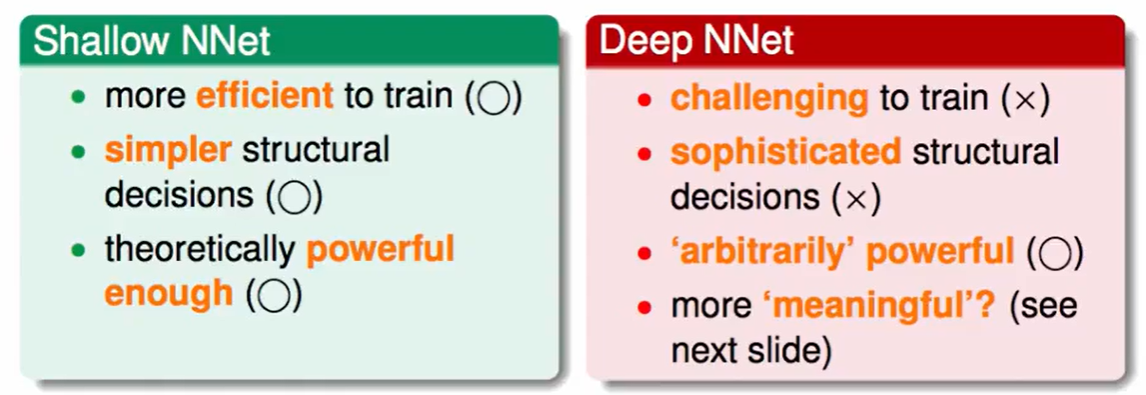
Deep NNet特点 :
训练很难
结构复杂,很多层很难决定结构
模型效果很好
层数变多可以获得更多的实际物理意义
实际物理意义举个例子,如下 :
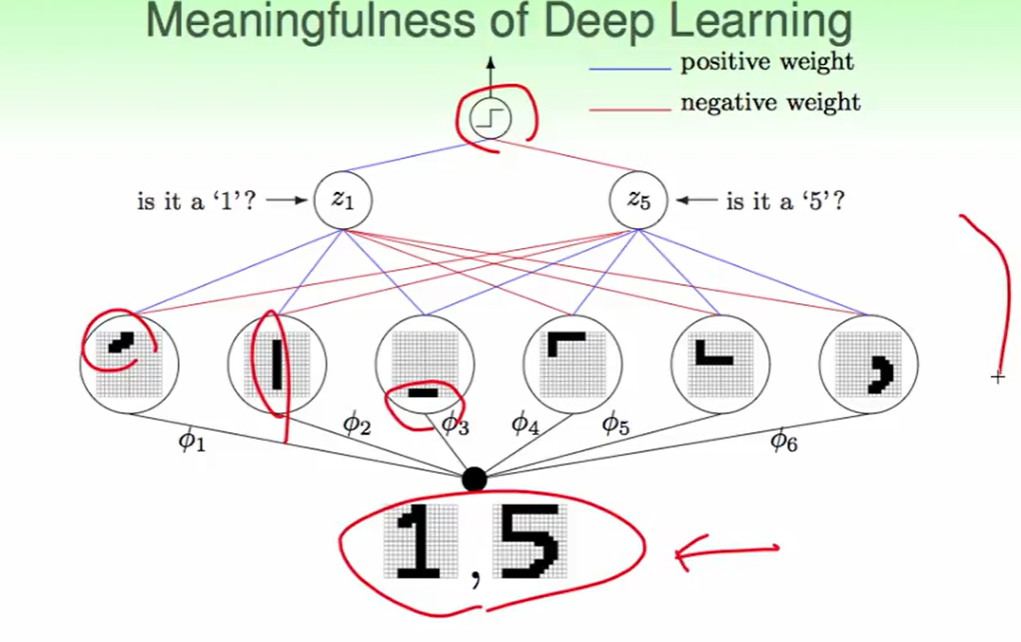
每一层的神经元都有他自己的物理意义,向着从简单到复杂feature的转换。
一些Deep Learning的chllenges和keys:
- 结构复杂

比如决定网络结构的时候,我们可以人为的做一些选择,比如图像识别,我们网络连接时,对于某个像素,我们只连接他周围的像素。
- 模型复杂

一般做视觉我们数据会很大很多,因此不用太担心。
同时也要做正则化,例如:dropout和denoising
局部最佳很难:

可以通过pre-traning来选择合适的初始化值,避免局部最小。
- 计算量大

现阶段的GPU 已经可以做很大的运算了。
Autoencoder
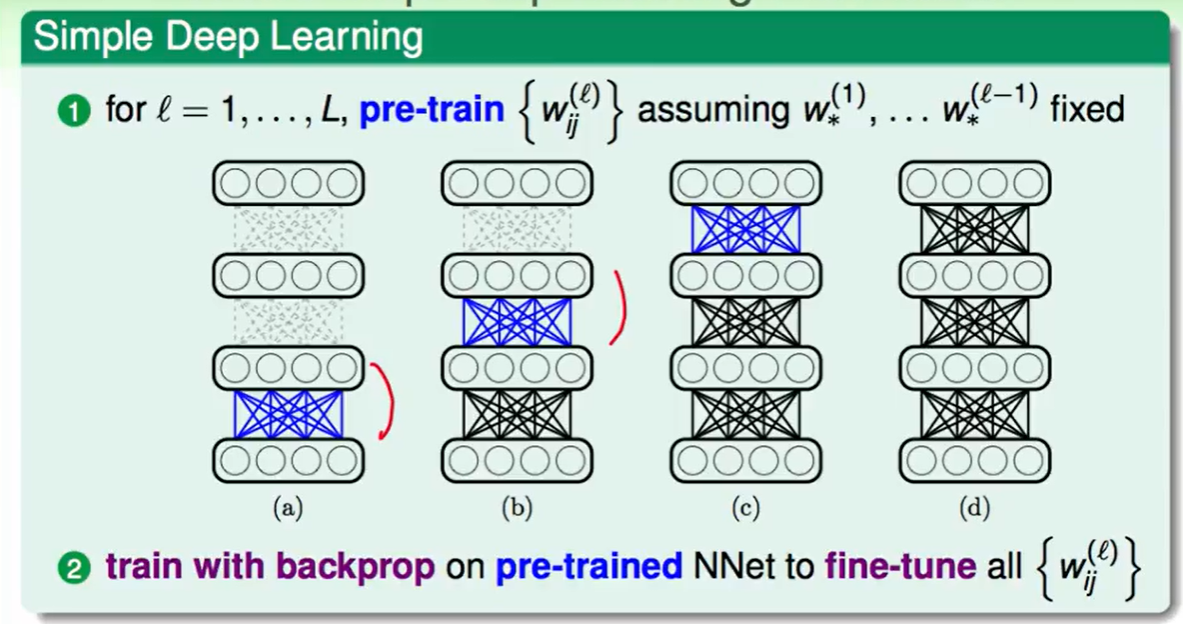
首先我们要对权重w的初值pre-training,它不用做到很好,能够帮助最后w迭代的快一些即可,同时帮助我们在一个还不错的地方做梯度下降,这样效果也会更好。
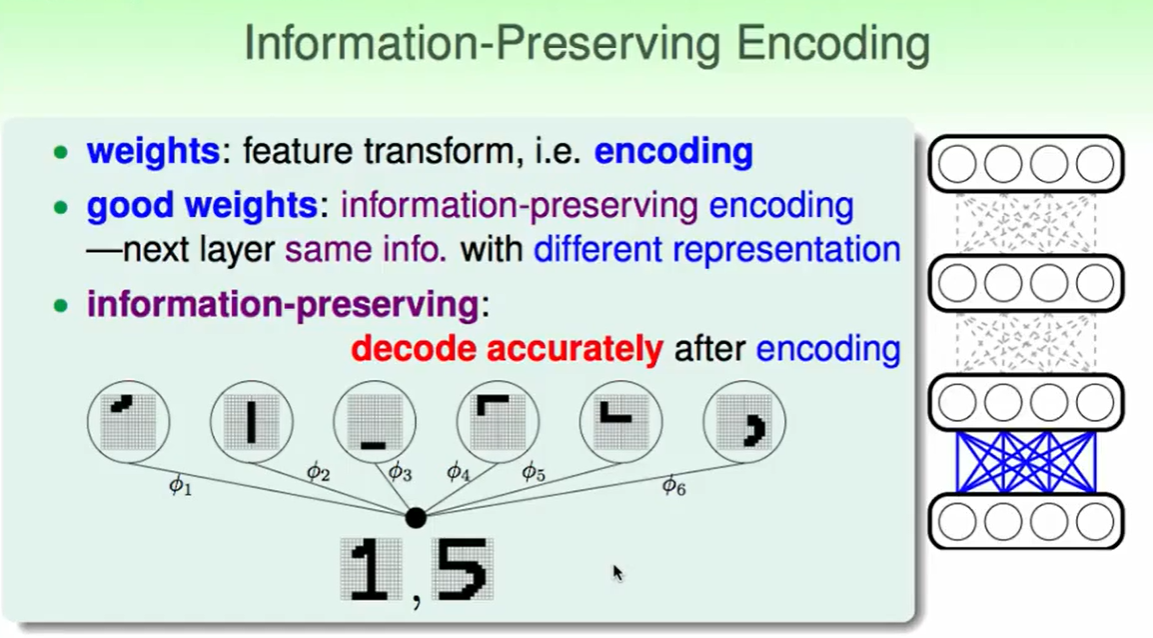
什么是好的权重? 可以保存原来的信息,只是比较简明精炼。如果你设计的把原来的资料搞得乱七八糟毫无规律,那么下一层也训练不出来什么好的效果。
一个比较具体的例子就是下图:
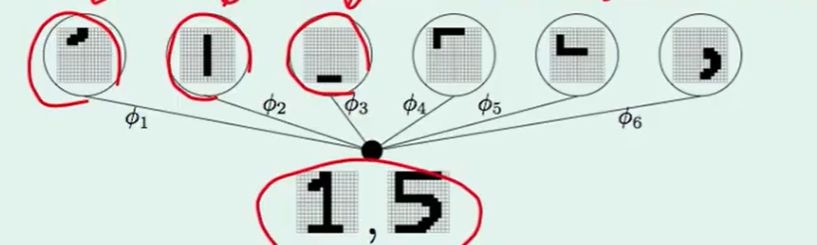
我们分开的这些小部分可以重建回来,那么它必然带着原来的信息,且更精炼,那么这个转换就是一个information-preserving(信息保留)的。
怎么找这么一个information-preserving的转换呢?
还是通过一个简单的神经网络:
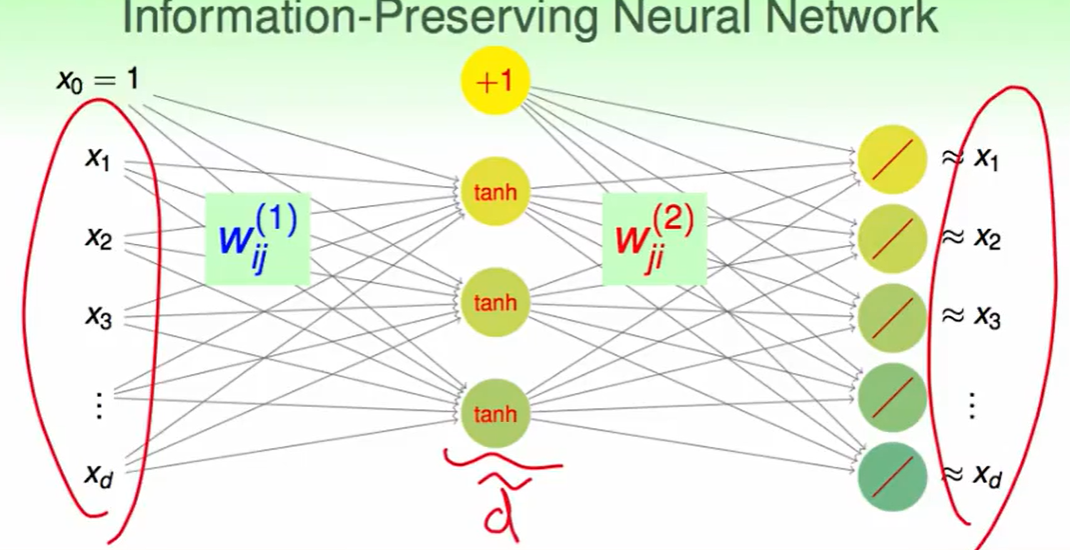
这个网络很有意思,最开始输入$x$进去,他输出还是$x$,这说明了第一次所做的转换可以反转回来,也就说信息得到了保留。
我们称之为autoencoder自动编码:

那么我们就是在让这个information-preserving Neural Network逼近一个不做任何转换的函数,这有什么意义呢?

这个逼近过程利用了一些数据的隐藏结构:
- 对于监督学习,这些隐藏的结构可以帮助我们做一个合理的transform,也就是学习数据所带的有效信息。
- 对于非监督学习,比如分布稠密的检测,这个transform可以告诉我们分布的稠密,我们就k可以知道数据起到主要作用的表达信息是什么。反着来看,我们还可以通过找到那些$g(x)! \approx x$,来看到是为什么差?为什么不合群。 所以可以告诉我们什么要的数据是一个典型的数据。
那么我们可以提出这个基本的Autoencoder的算法:

训练数据很简单就是 (x,y=x),因为我们想让它输入输出一样。
我们通常希望第二层的神经元数量要少于第一层,因为我们希望得到的是精炼的信息。
可以用backprop训练,层数不多很容易训练。
有时我们会加上这个限制:$w{ij}^{(1)} =w{ji}^{(2)}$,这个很容易理解,这个权重怎么送过来的就怎么传回去,这样做完后如果能够按照转化来的时候的方法转换回去,那么信息说明得到了保留。
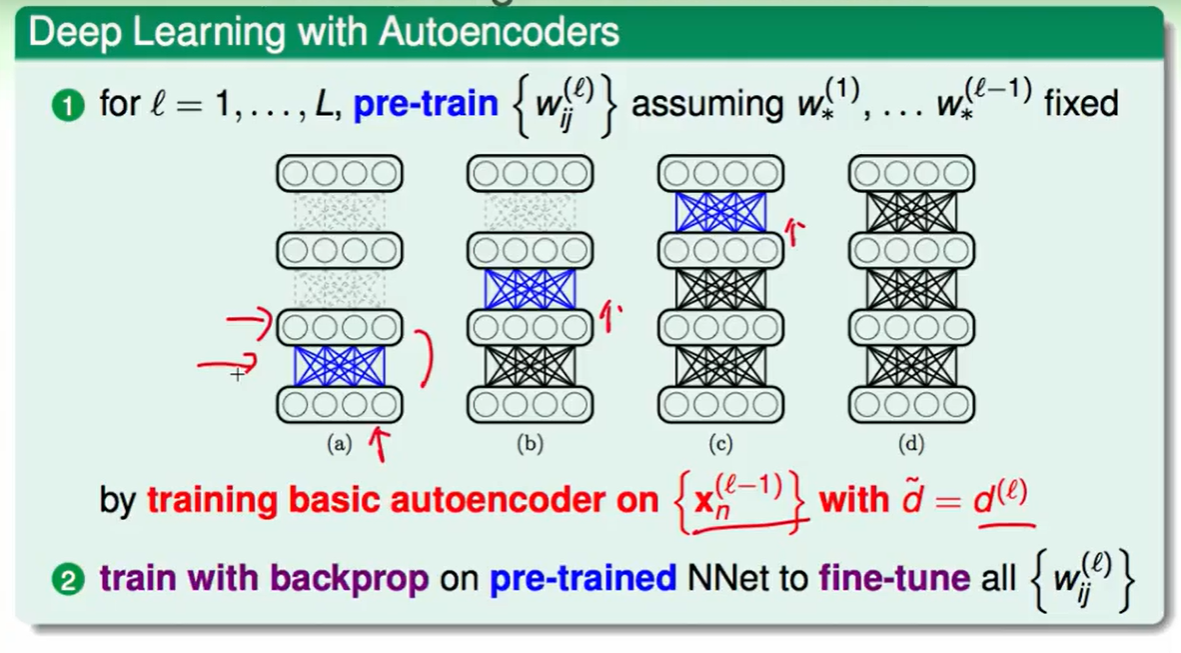
那么我们对每一层来做即可,得到每层的初始权重。
Denoising Autoencoder
由于深度神经网络模型复杂,我们要小心overfitting,可以添加一些regularization:
- 比如网络结构限制的简单一些
- 比如上一章所提到的weight-elimination regularizer 或者是weight decay regularizer
- early stopping
除此之外,我们还有一种方法:
先回顾一下overfitting的原因:
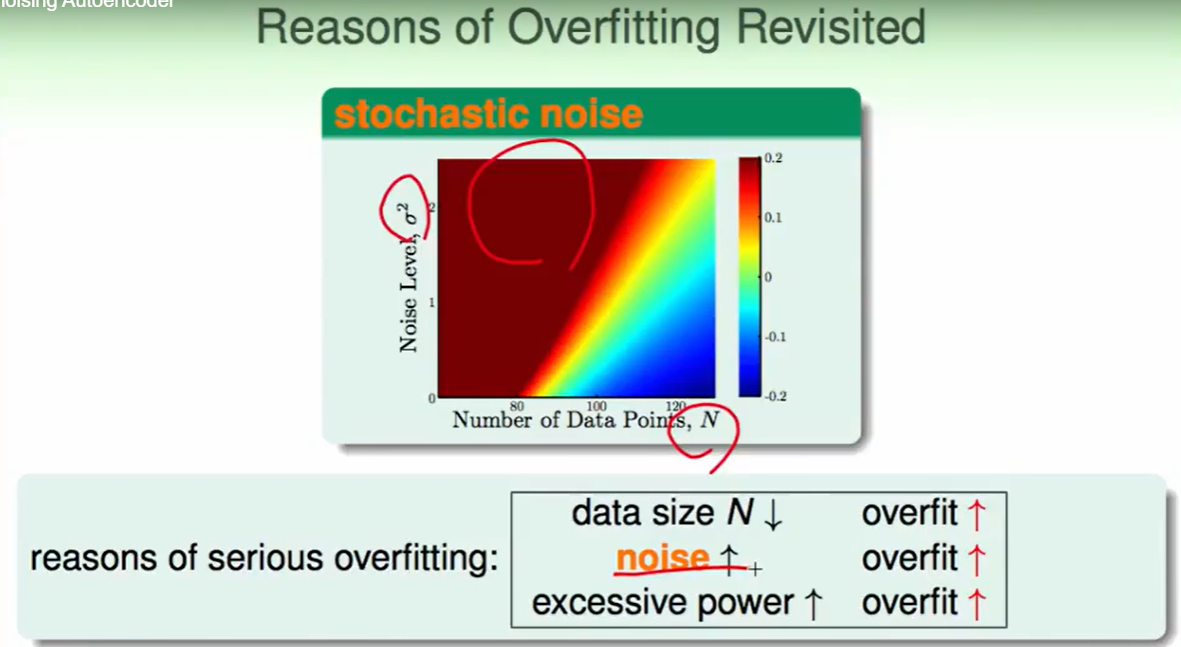
一个直观的想法是:我们直接去掉noise,这样noise少一些,overfit就会减轻一些,但是这样并不容易做到。
想让网络鲁棒性更强,我们甚至可以主动喂给autoencoder网络一些noise!
这个想法非常反直观,我们换个角度来想,如果我们在训练autoencoder的时候放一些noise,比如写的很丑的数字一,但是我们依然把他的输出期望设置为干净的1。那么我们的encoder就有了一种去除杂质的功能。

我们称之为denoising autoencoder,具体就是训练数据上的输入加一些noise,输出不变,用这样的数据去训练一个denoising的encoder。
这样做出来的权重一定程度上表达了我们需要的性质,也获得了一定的去杂质功能,这也是一种regularization的方式。
Principal Component Analysis(PCA)
autoencoder不是一个线性模型,里面包含tanh()。
我们现在考虑线性的autoencoder:

考虑一些特殊的条件:
- $x_0$我们会拿掉,这样就保持了输入输出维度一致
- 限制$w{ij}^{(1)} = w{ji}^{(2)}=w_{ij}$: 正则化
- 假设中间层的维度小于输入输出两侧的维度,为了压缩精炼信息。
不妨另$W = [w_{ij}]$,这是一个$d* \tilde d$维的矩阵。
那么我们就可以推出新的用$W$表示的$h(x)$
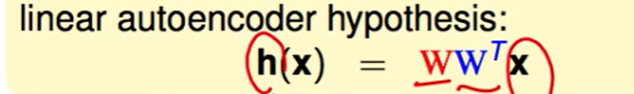
我们的error measure function $E_{in}$就是变化后和希望得到的结果的平方差,而我们希望得到的恰好是我们的输入,那么表达式就是:
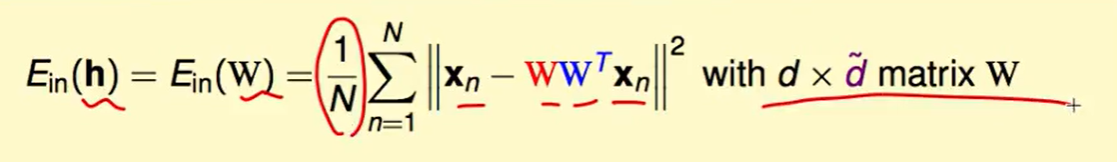
我们尝试去解他的闭式解:
$WW^T$首先可以做特征分解(也叫谱分解/酉相似对角化):

- $d*d$维的矩阵$V$的每一行向量是互相垂直/正交的(orthogonal):所以$VV^T=V^TV=I_d,I_d是一个单位矩阵$
- $\Gamma$是一个对角矩阵,这个对角矩阵,对角上的值是$W$的特征值,非零项最多有$\tilde d$个,这个不难理解,因为我们的$W$是一个$d*\tilde d$的矩阵,那么他的秩最大是$\tilde d$。
$WW^Tx_n = V\Gamma V^Tx_n$
- 我们从几何意义理解这个式子,$V^Tx_n$可以看作对$x_n$做一个旋转或平移
那么$\Gamma V^Tx_n$就可以看作,我们把$V^Tx_n$ $d$到$\tilde d$维的数据变为了0,然后放缩了其他项
$ V\Gamma V^Tx_n$,表示我们最后在旋转回来
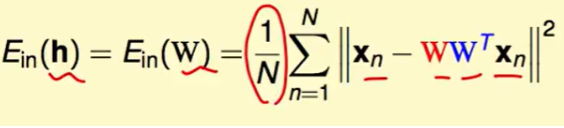
那么这个公式前面的$x_n$也可以看作:$x_n = VIV^Tx_n$,$I$是单位矩阵。
那么现在把问题转化为了$W$最佳化问题转换为了$\Gamma$和$V$最佳化的问题:
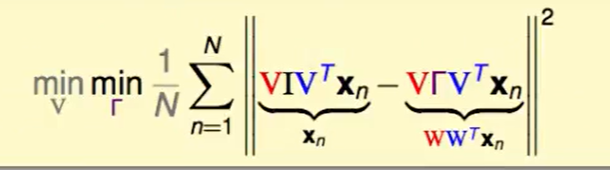
首先红色的$V$代表back-rotate,就是第一次旋转/反射 的逆变换,这不会影响长度,所以我们暂时可以把他们去掉

我们想要先考虑里面一层最小化$\Gamma$的问题: 也就是说我们想要尽可能多的0塞入$(I-\Gamma)$这个对角矩阵中,这样就可以减少这个表达式的值。由于$\Gamma$的$rank\le \tilde d$,因此我们不失一般性的设$\Gamma$长这个样子:

那么下一步我们就去做$V$的最佳化维题:
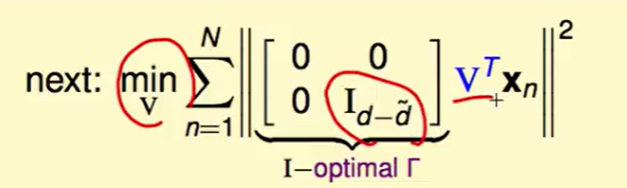
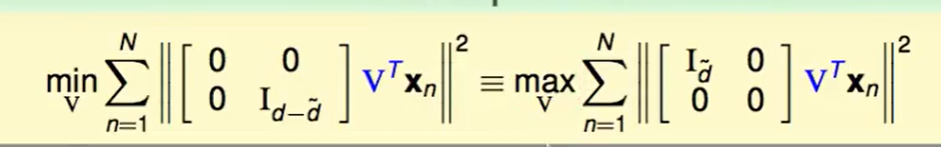
首先把最小化问题转成最大换,原来代表的是留下哪儿些维度,希望他们最小,这就等价于拿掉哪儿些维度,希望他们最大。
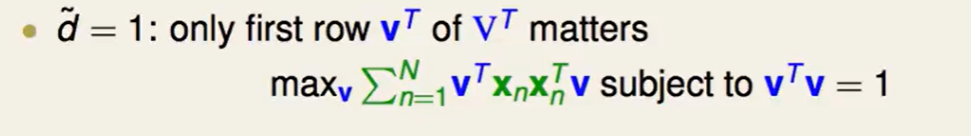
首先只考虑是对角上非零的个数只有一个的情况:
由lagrange multiplier可以得到:
我们对两边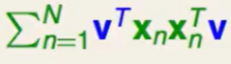 和他的限制条件
和他的限制条件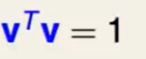 分别求导后,最优解是可以使得两个导数平行,即:
分别求导后,最优解是可以使得两个导数平行,即:

这么看来$v$就是这个绿色部分就是的特征向量!

那么在$\tilde d = 1$的情况下,最优的$v$就是 $XX^T$的最大特征向量。
拓展到$\tilde d$不限制为1的情况下:
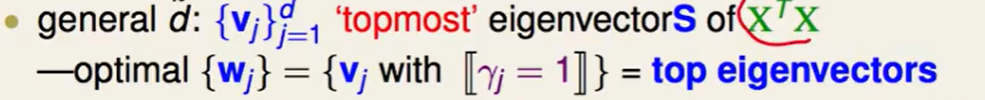
我们找最大的几个特征向量即可,这就是我们最好的$V$
因此linear autoencoder就是在告诉我们:我们拿到一个数据矩阵,我们对他做特征分解,找出最大的几个特征向量,这几个特征向量就是最符合$x_n$的向量,我们最应该做投影,做特征转化的向量。

Linear Autoencoder算法:


因此这个算法可以帮我们最大化投影后的效果。
他主要用在PCA(Principal Component Analysis,主成分分析)上,主成分分析中希望我们最大化 一个差值:$x- \overline x$,即投影后的变化量最大。
其实PCA算法就是:

也就是说把一个高维的数据找到一个线性上表现最好的形式。
这也是PCA的主要作用:降维
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!