CH14：Radial Basis Function Network

RBF Network Hypothesis

首先回忆一下Gaussian Kernel在SVM中的应用

我们在$x_n$处找$\alpha_n$ 来组合Gaussian Kernel，使得实现最大边界。

高斯核也叫径向基(Radial Basis Function，RBF)核。其中radial代表我们今天算的和距离有关，也就是$x$和中心$x_n$。

我们今天就是要做radial hypothesis的linear aggregation。

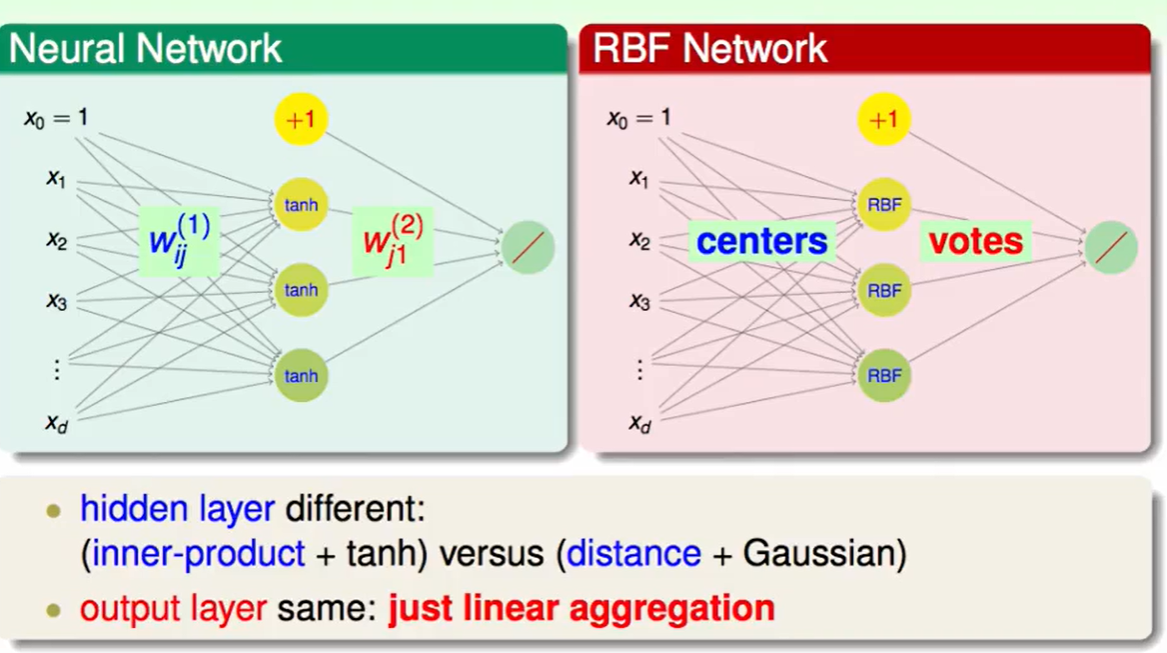
RBF Network和Neural Network的区别是：Neural Network是先和$w$做内积然后tanh转化，而RBF Network是通过把输入看成centre，然后去做距离的RBF Function。

这两者的输出反而没什么区别，都是linear aggregation

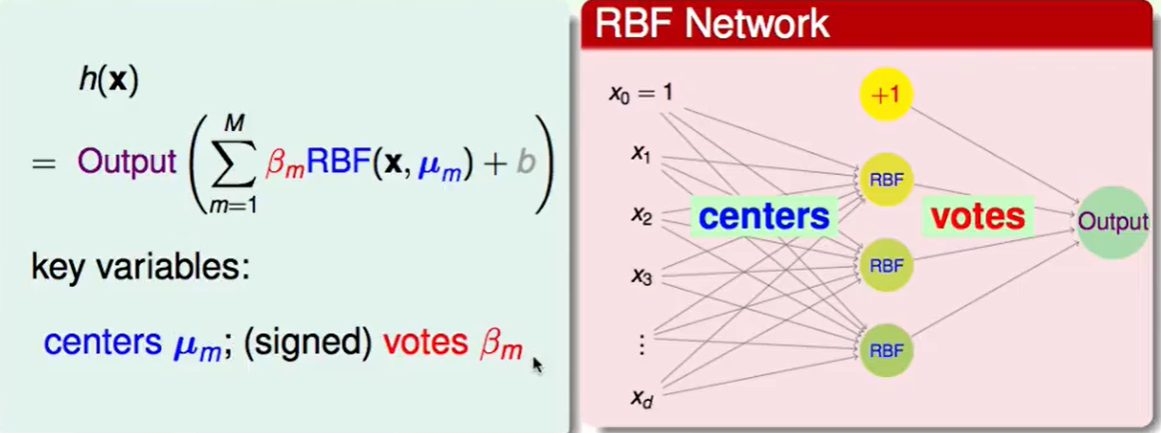
那么我们应该关注的两个变量就是系数$\beta_m$和中心$\mu_m$。

output采用的是sign(),也就是二分类，M就是support vector的数量。

我们在kernel中提到kernel通过把两个向量转换道z空间，找到他们的相似性。

相似性是一个很好的定义特征转换的方法，RBF中通过距离的相似性做feature transform。

RBF Network Learning

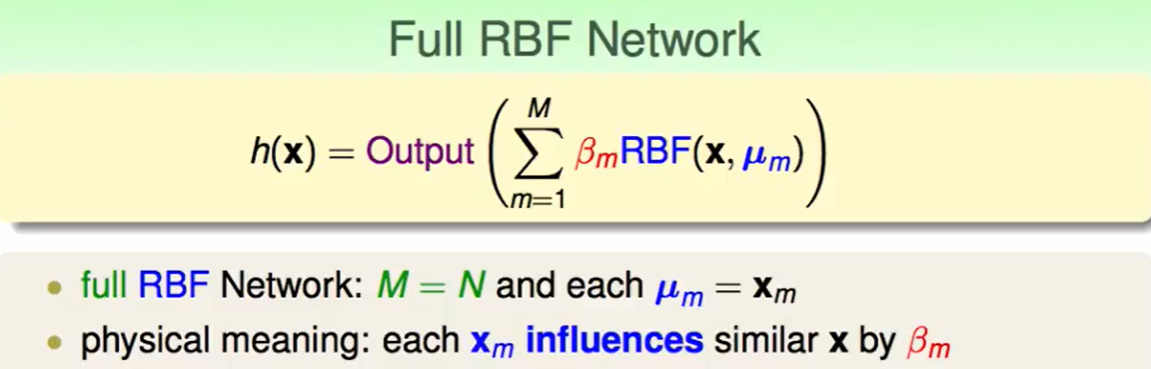
我们定义一个Full RBF Network，他有N笔资料，那么就有N个中心，他的物理意义就是：我的每笔资料对会对周围资料有影响，影响力大小为$\beta_m$。

比如Uniform的方法：

我们通过大家意见的相似度来整合每个人的意见，把所有点都当做中心点。

高斯函数是一个幂指数函数，他的下降非常快，因此那个最接近$x_m$的$x$掌握了主导权，那么我们是不是就不用考虑每个人了，找出主导权的来做决定就好了。

我们考虑有主导权的那个$x$(最接近$x_m$的$x$), 用他的投票$y_m$代替所有的人。

这应该叫做selection而不是aggregation了。

这叫好比找中心$x_m$的最近的邻居，我们称之为最邻近模型。

我们可能一个来代表所有人还是有点太不合理了，那么我们考虑最有主导权的k个$x$, 也就是距离中心最近的k个邻居。

那么我们考虑最佳化这个$\beta$就好了：

我们先把他看作一个linear regression的问题，然后用square error去衡量错误。

那么我们的资料就是这些 RBF Function组成的资料：

最优化$\beta$ ? linear regression很容易做到这个问题，这是有闭式解的：

$Z$矩阵的大小是一个NN的，即每个点距离每个中心的RBF Function。那么这肯定是一个*对称矩阵，因为a到b和b到a的距离必然相同。

有一个theoretical fact：如果$x_n$各不相同，那么$Z$就是一个可逆的。证明这个很容易，如果存在$x_1=x_2$,那么Z的第一二行会相同，第一二列也会相同，那么这明显就不是满秩的了，也就是说不可逆了。

那么我们的$\beta$表达式可以写成：

full Gaussian RBF Network中的$\beta$做完回归后：

这里推到发现：$g_{RBF}(x_1) = \beta ^TZ^{-1}(Z的第一行)$，这就得到了一个很有趣的结果：

$g{RBF}(x_n) = y_n$,这就说明我们的$E{in} =0$， 但这感觉有点怪怪的: 可能回有overfitting。

那我们加上正则化：那么我们用ridge regression来做：

其中$\lambda$是一个正则量，代表着正则化的程度。

在kernel ridge regression中我们对无限多维的转换做regularization，在RBF Network中是对有限多维做regularization。

我们考虑考虑不让所有数据来做中心，考虑一部分有代表性的来做中心即可，那么就可以减少overfitting了。

K-Means Algorithm

如果$x_1$和$x_2$相近，那么就没必要搞两个中心，聚类时选一个看作中心即可。

现在先做一个聚类，分成M个集合，我们希望每个集合中的中心和这个集合中的数据是相似的。

我们还是先做一个error measure function：

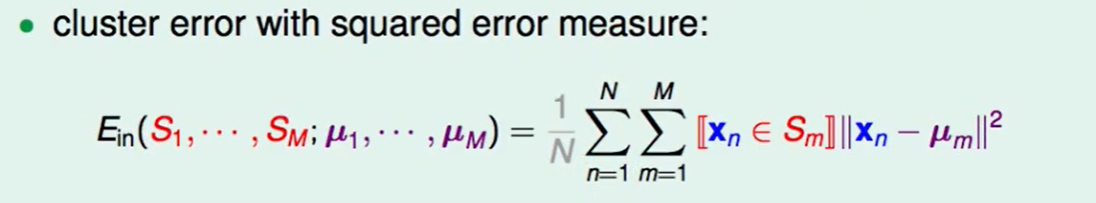
采用square error，对每个集合来说，找出这个集合中的每个点和中心点的距离差。

但这个貌似并不好做最优化，因为有两个优化要做：一个是排列组合问题：怎么分开不同的集合，另一个是中心点怎么选择的数值优化问题。

如果中心点确定了，那么我们选择距离某个中心点最近的中心点即可。

那么没了分组的问题 ，我们可以直接做数值优化的问题了：

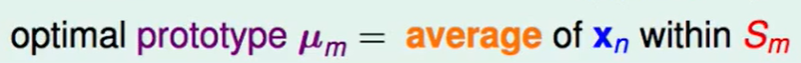
那么最佳的$\mu_m$就是每个集合内$x$的平均。

那么K-Means算法就可以提出：

• 初始的$\mu$怎么选：一般来说从$x_n$中随便选取k个即可

• 怎么停止？会停止吗？

  

  当然会，集合不变化后，$E_{in}$是逐渐变小的。

同时也可以提出RBF Network Using K-Means算法了。

• 用非监督的方法K-Means来帮助我们精炼到了feature transform，就像autoencoder一样。

• 参数选择：怎么选择M，$\gamma$ ? 还是Validation : )

老实说，RBF Network是一种old-fashion的model，他和Gauss SVM，Neural Network可能表现没什么区别，但是它可以帮我们连接一些我们已知的算法，建立一个完整的算法体系。

K-Means and RBFNet in ACTION

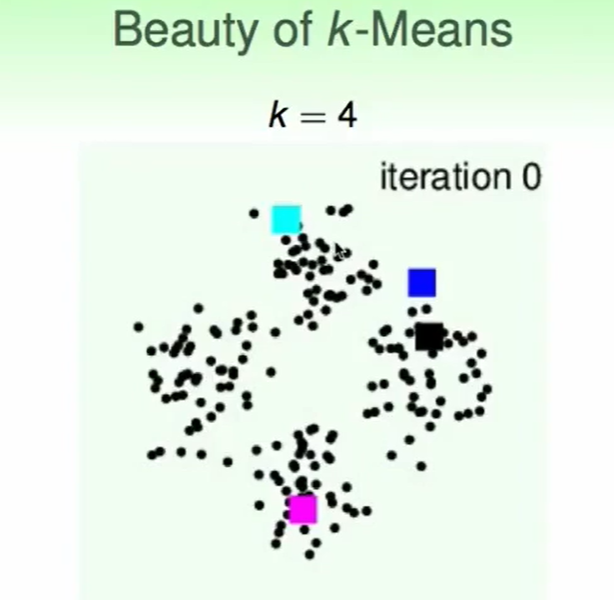
一个K-Means的Demo：

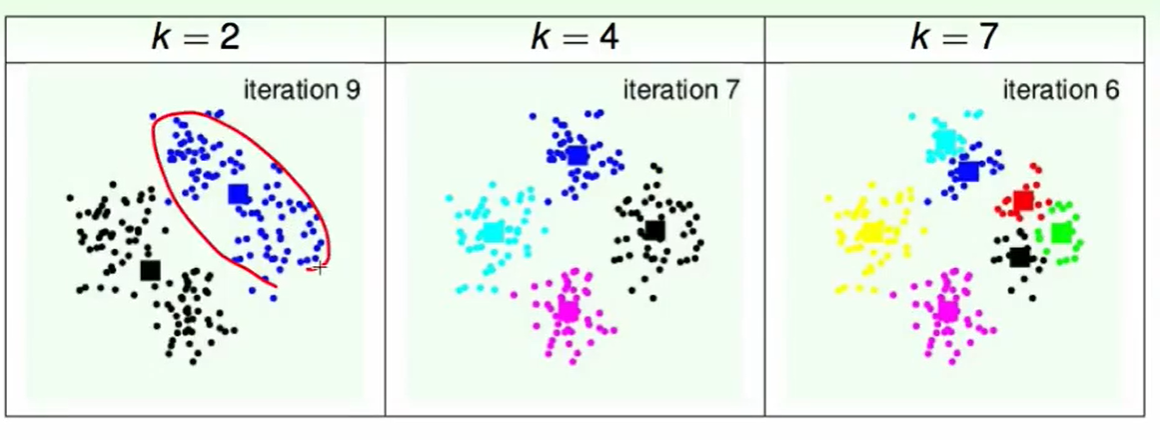
不同的k的区别：

我们可以用这些K-means做的结果，用RBF Network using k-means去做binary classification：

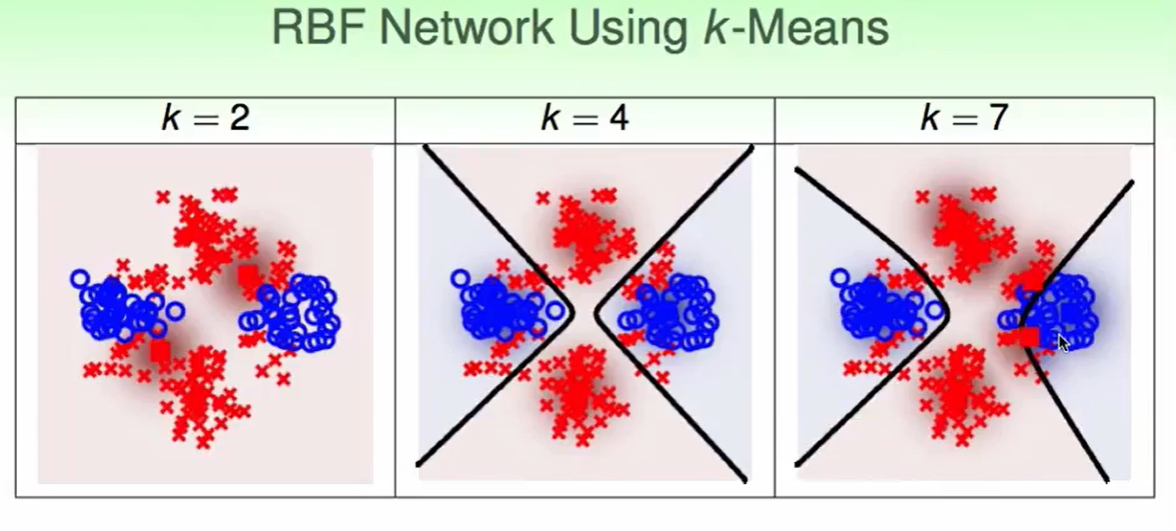
如果我们第一层的K-Means做的比较合理，那么RBF Network来做也是很轻松的，随着K的变大,RBF Network的feature transform的维度也更大，边界会更精准一些，但是要小心overfitting哦。

我们最后来看Full RBF Network：

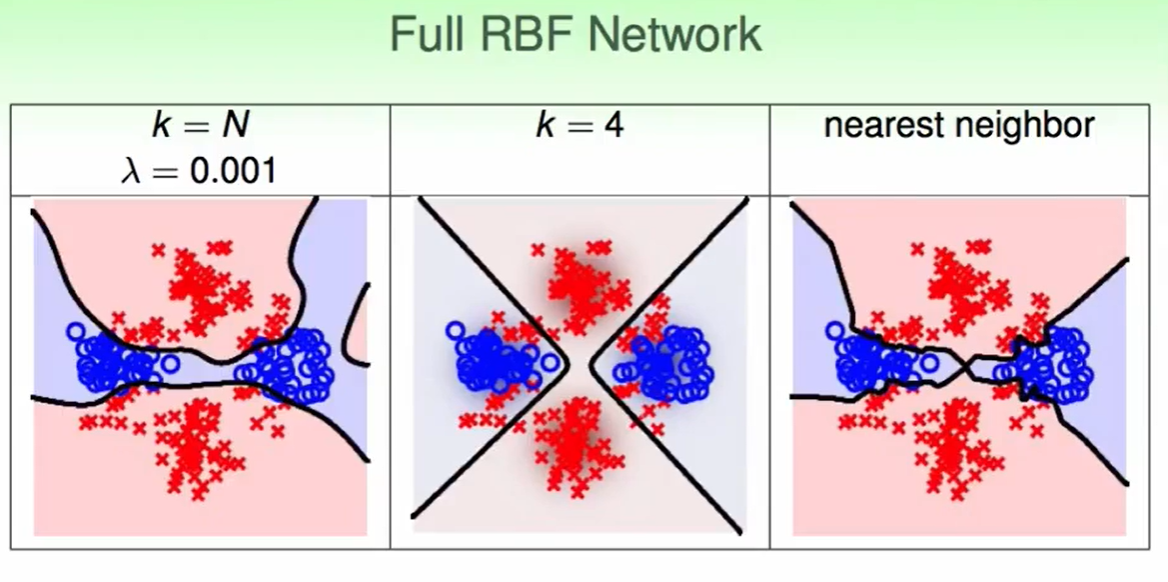
值得一提的是:Full RBF Network因为要考虑所有的点，因此计算量很大，比如nearest neighbour这种方法，他很依赖于一些几何上的算法，来计算的快一些