介绍神经网络

反向传播(backpropagation)

梯度的计算是通过计算图 ：

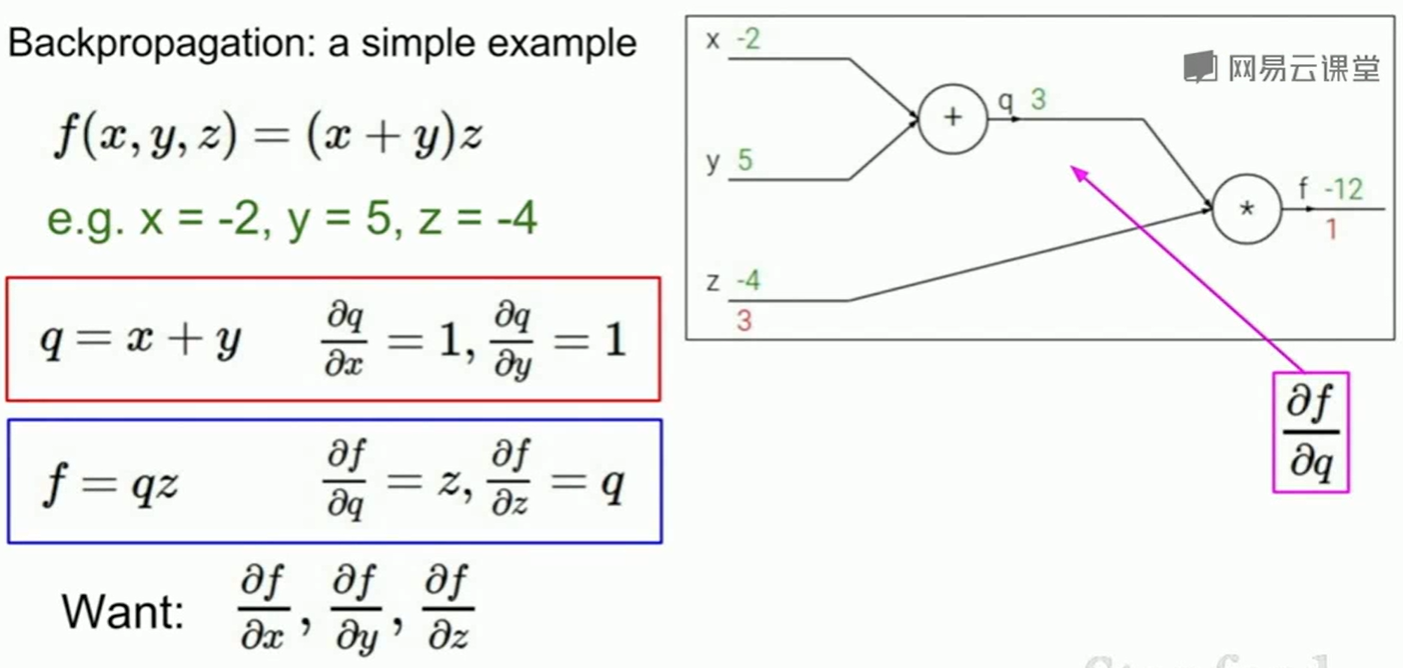
链式法则告诉我们，我们只需要把计算图上的每一段相邻的梯度算出来，我们连乘上他们就是最后一个变量对最前面一个变量的梯度。

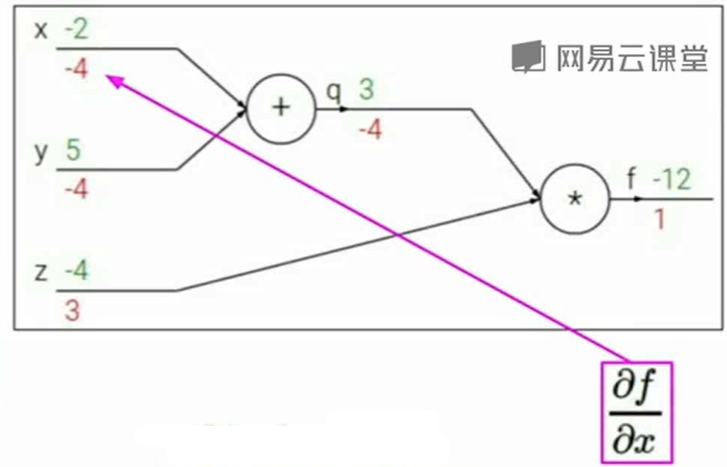
backpropagation的运行方式：

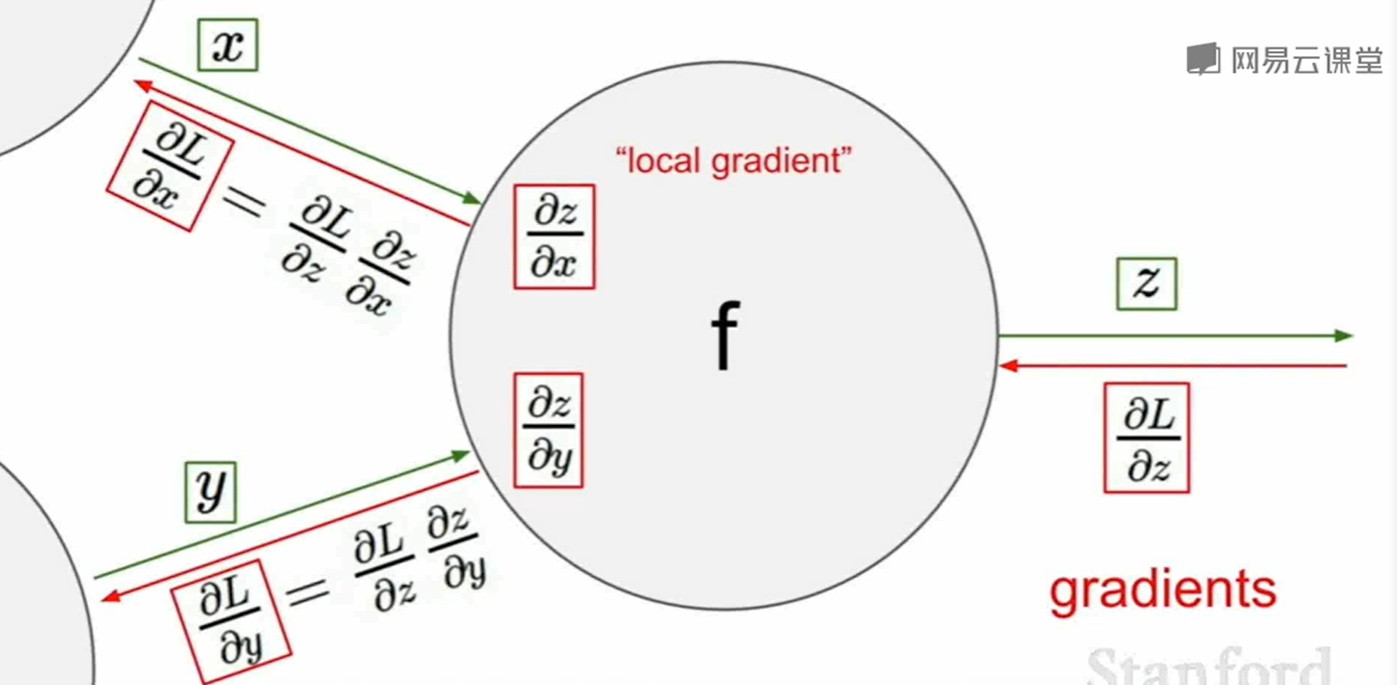
一个比较复杂的例子：

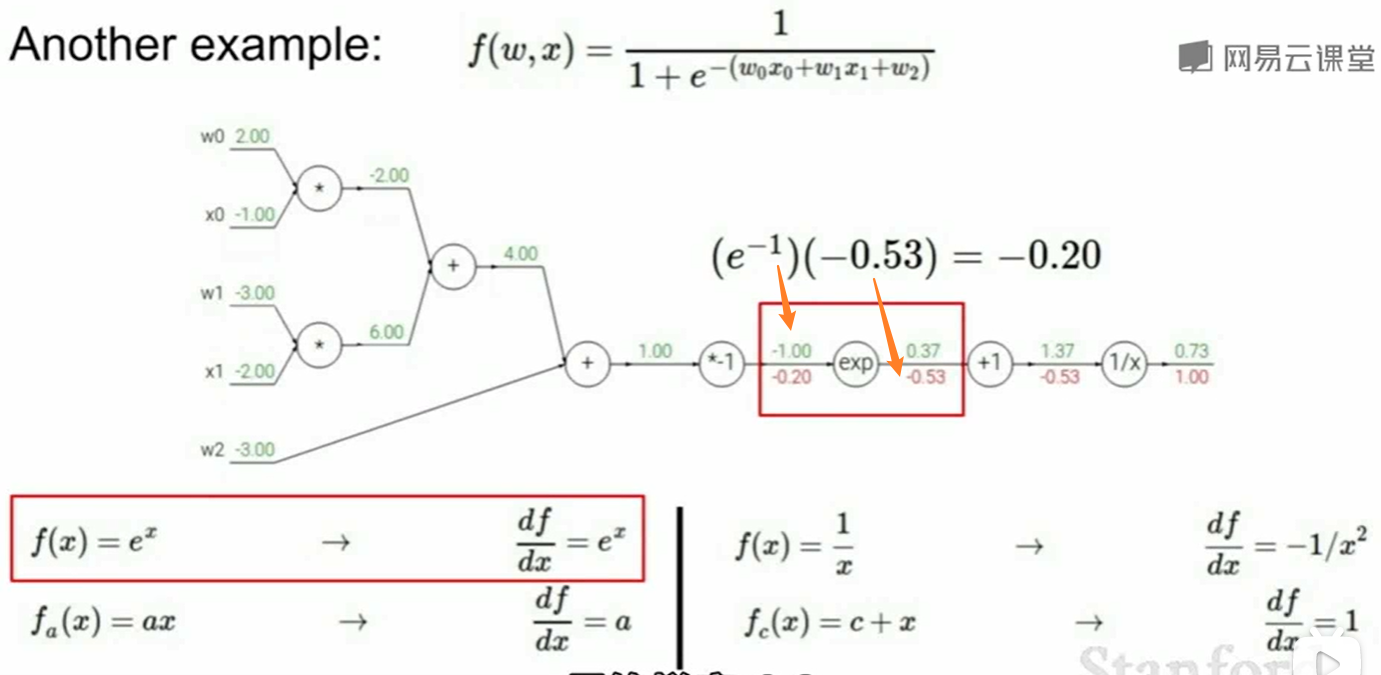
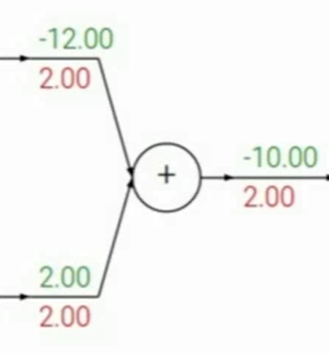
对于add门，求对两边梯度都是1，因此直接传过去梯度upstream gradient即可：

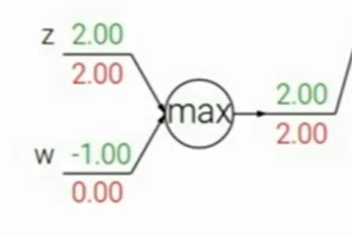
对于max门，local gradient只会对其中较大的一个变量的梯度1，另一个为0.

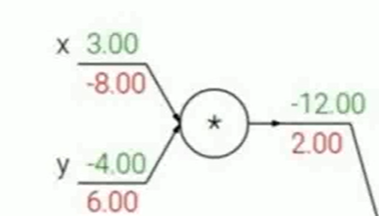
对于mul门，对其中一个求梯度就是另一个变量的值，如下图，xy对x求梯度就是y，也就是-4，然后upstream gradient是2，2\(-4)=-8

假如变量是高维的，做法和刚才一样，只不过我们的梯度变成了雅可比矩阵。

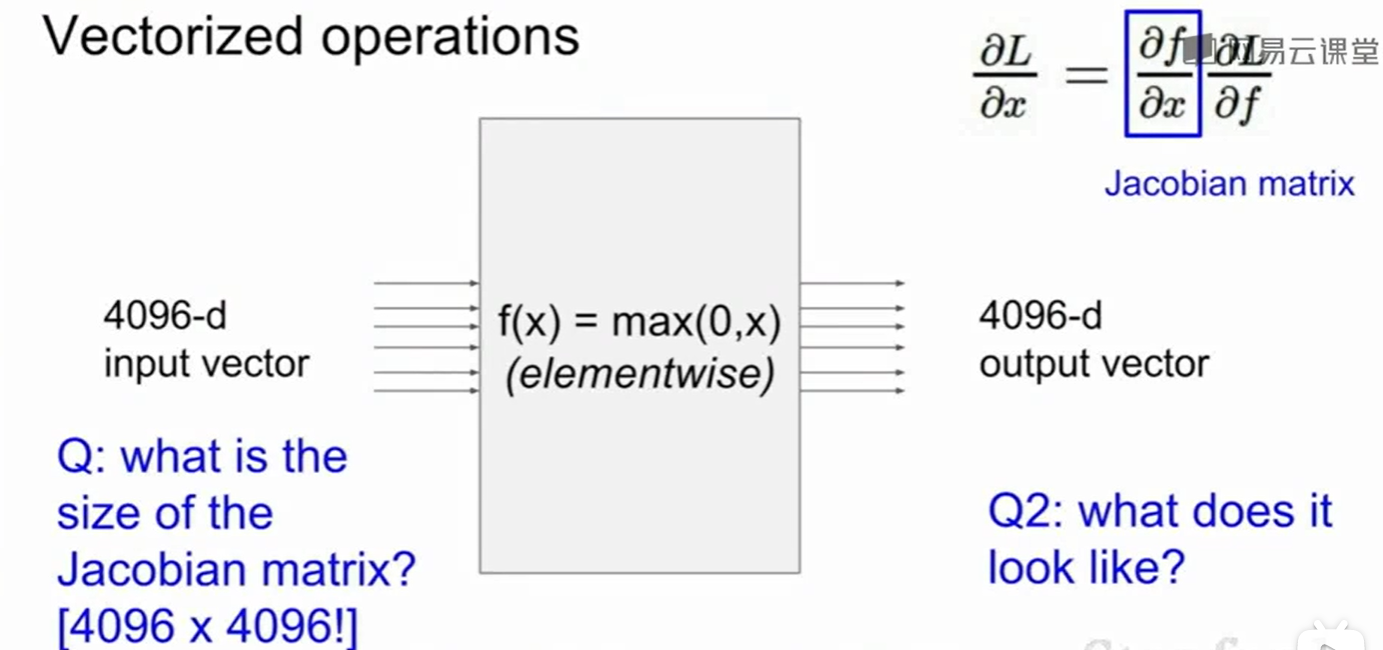
如果我们对向量求导，即x对每个4096维的向量的每个元素求偏导，那么结果这个雅可比矩阵就是4096*4096的矩阵，这个矩阵太过于大了。

其实这个矩阵存在大量0，我们只需要记录非零项即可，这样就大大减少了空间的开销。

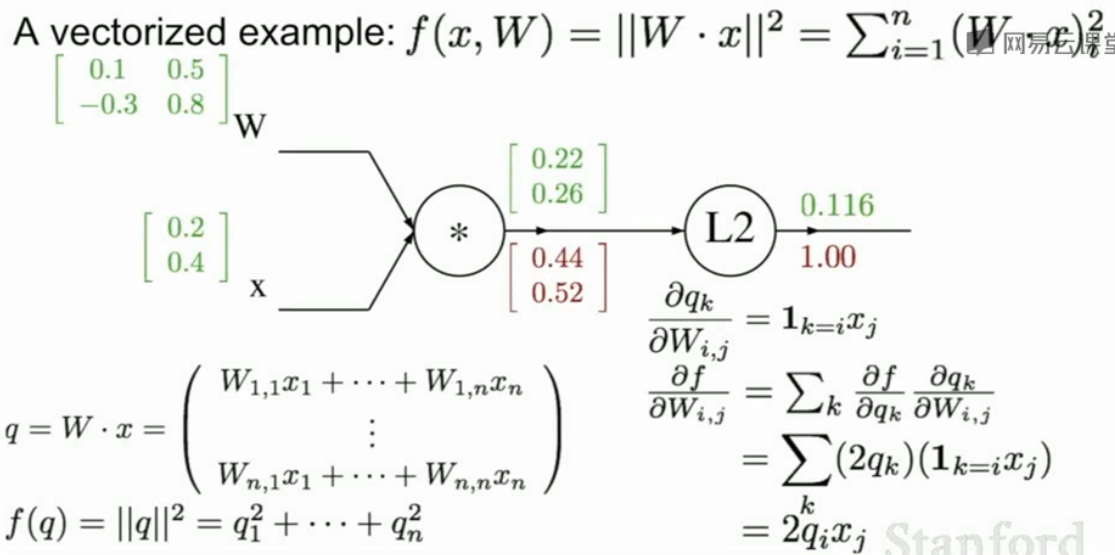
所以梯度就是：

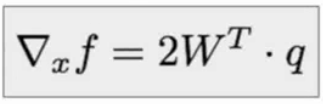
神经网络(Neural Network)

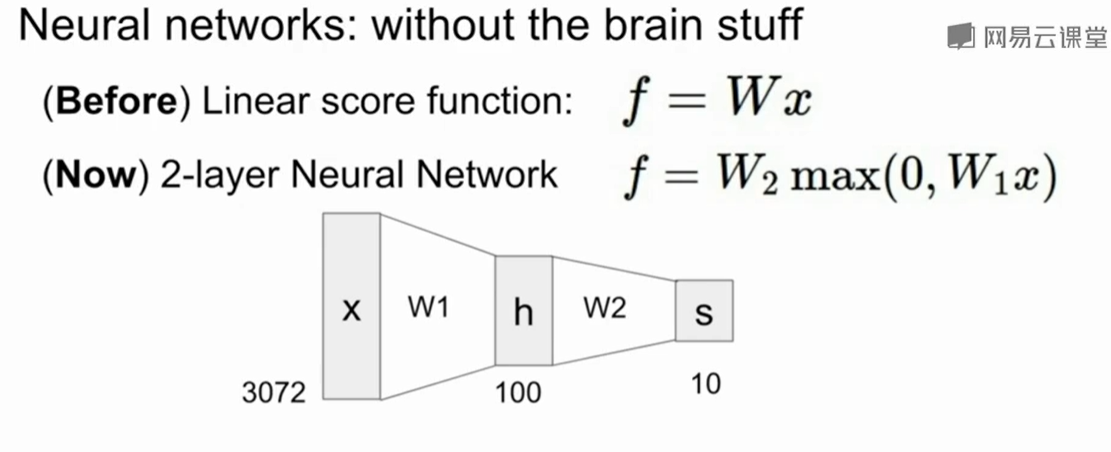
$f=Wx$是一种最简单的线性的网络。

我们可以组成一个两层的网络，其中一层是$W_2$，另一层是$max(0,W_1x)$，这一层将网络变成了非线性的，这是因为$max(0,W_1x)$本身不是一个线性的函数。

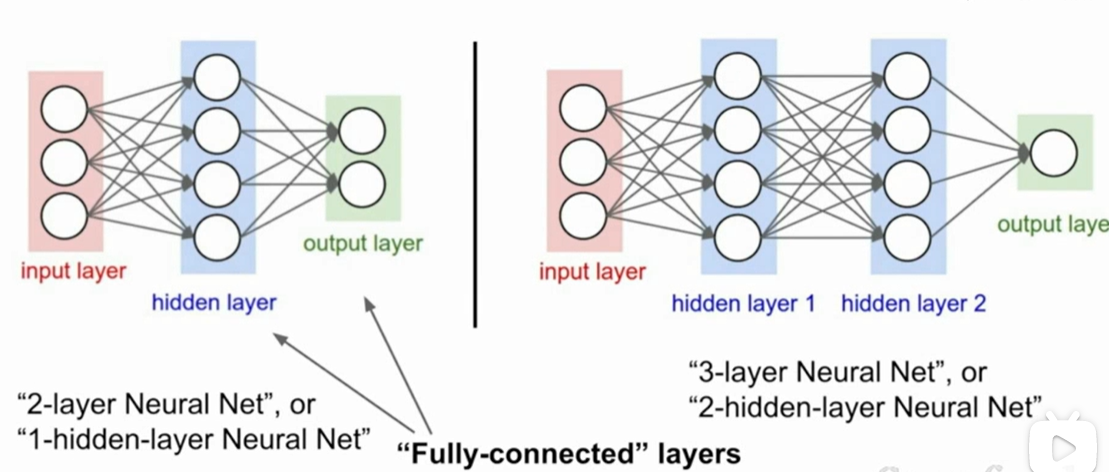
扩展到多层网络：

一些激活函数：

神经网络的叫法： 一般我们更喜欢叫 k层神经网络，k=1(a input layer)+hidden layer层数.