马尔可夫决策过程(MDP)—下

本次课的plan list：

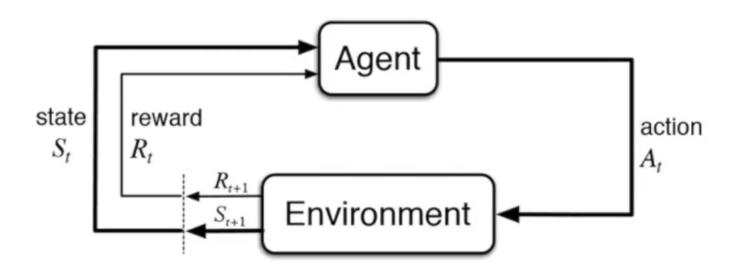
环境和agent交互的过程可以通过马尔科夫决策过程来表示。

马尔可夫决策过程可以解决许多实际问题，因此这是RL种的一个基本框架。

一般来说MDP的环境是fully observable的，但其实partically observable也是可以通过MDP来解决的。

如果一个状态转移是符合马尔可夫的，那么说明当前的状态只与上一时刻有关。

即：

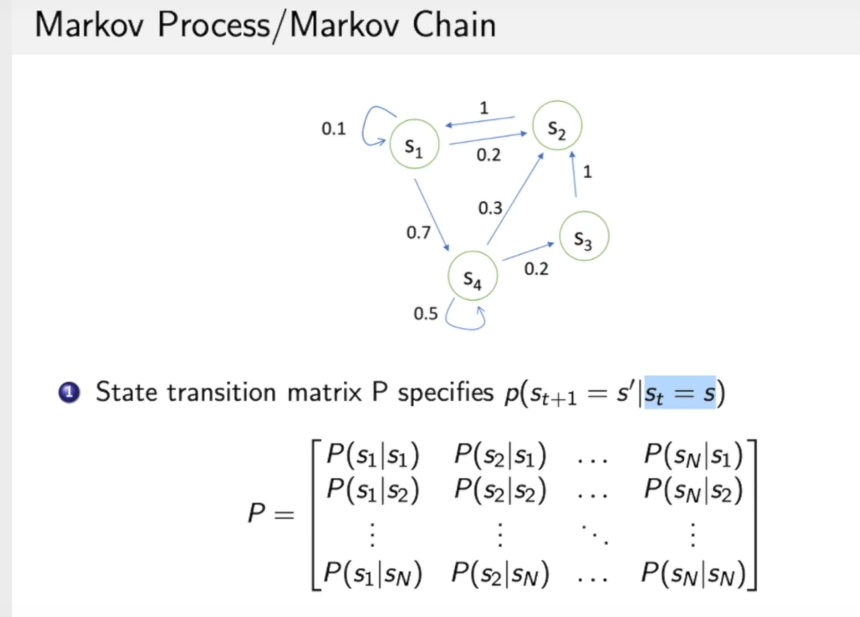
上图可以看作：在当前状态转移到其他的概率，我们可以用一个状态转移矩阵来表示，可以看作是一个条件概率，即在当前状态下到达其他状态的概率。

这个图可以看作马尔可夫链，一个例子：

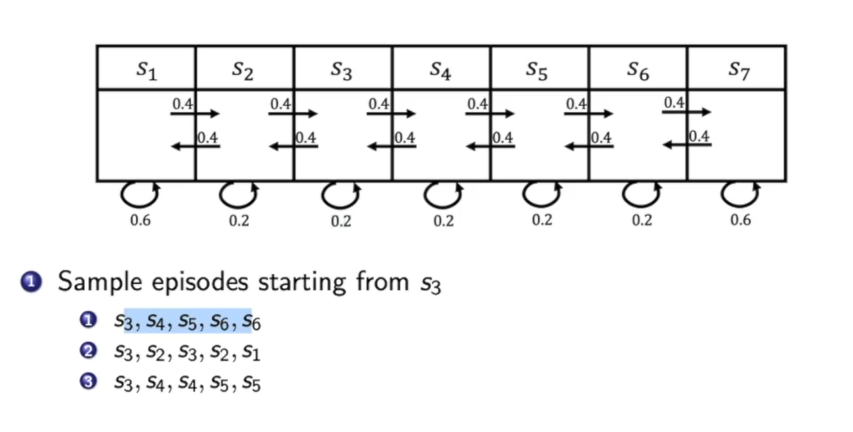
马尔可夫奖励过程（Markov Reward Process）：

马尔可夫奖励过程 = 马尔可夫链 + 奖励函数

现在我们给上述例子中的马尔可夫链加上奖励：

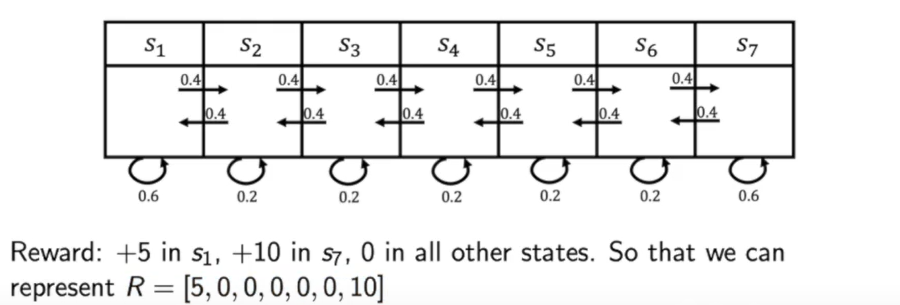
奖励可以用一个向量$R$来表示。

马尔可夫奖励过程 中Return的定义：

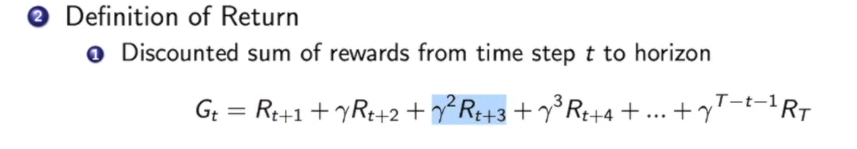
这里面包含一个折扣因子，距离我们越远的汇报折扣的越多。

马尔可夫奖励过程 中value function的定义：

可以简单理解为从未来获得奖励和的期望

为什么我们加上了discount factor $\gamma$ 这个东西呢？

• 首先他很好的避免了环状的马尔可夫过程，避免了无穷的奖励

• 我们希望尽可能快的得到奖励

• 人和动物对立刻奖励有更大的倾向

当马尔科夫过程中的$\gamma$设置成1时，我们就把未来的奖励和当前立刻可以获得的奖励看成等价的，而把$\gamma$设置成0，说明我们只关心立刻获得的奖励。一般我们把这个$\gamma$当成超参数。

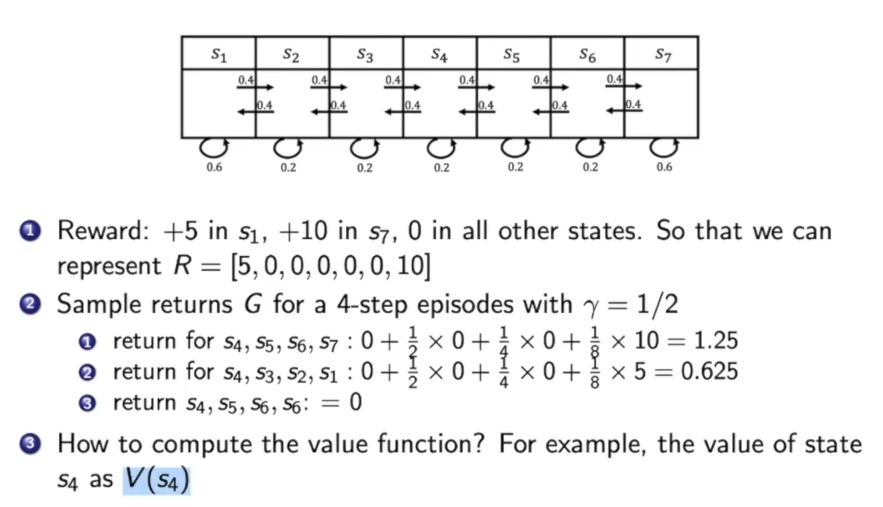
对于$s_4$我们如何计算在此处的价值呢？

我们可以从$s_4$开始移动，获得各种路径，再把路径所获得的reward传回来。我们可以蒙特卡洛计算，也可以通过下述的Bellman equation来算：

计算马尔可夫过程的价值：

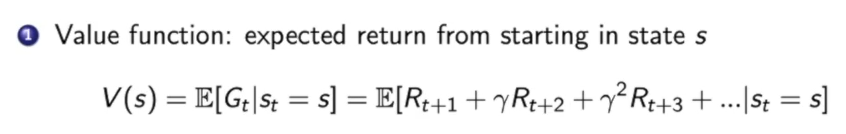
首先value function的公式如上

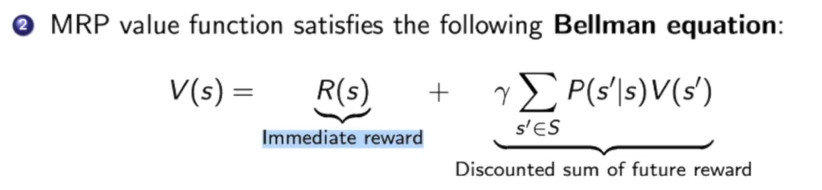
我们可以给他换个写法：

也就是bellman equation。

Bellman Equation：

Bellman Equation 定义了当前状态与下一个状态的关系

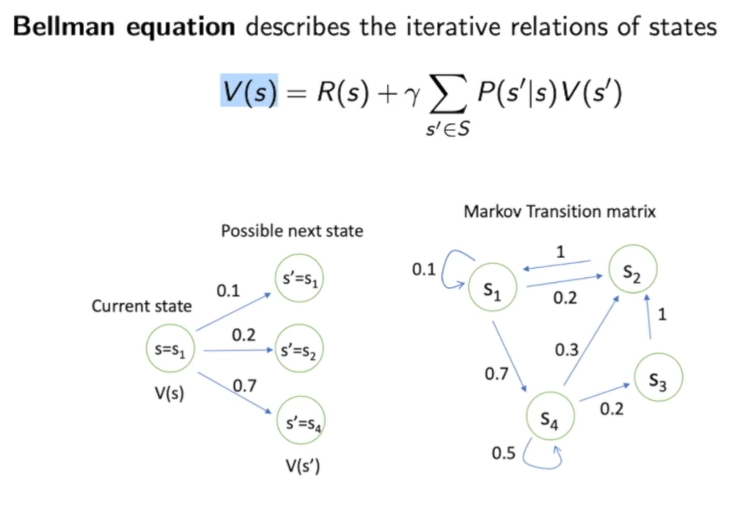
我们可以把bellman equation改写成矩阵形式：

那么我们在此时就可以推导出矩阵V的形式：

$$V = R + \gamma P V\\ V = (I-\gamma P)^{-1} R$$

但矩阵求逆的复杂度是$O(n^3)$,因此这种直接求逆的解法只适用于少量状态的马尔可夫过程。

我们可以通过迭代的方法解决大型的马尔可夫过程：

• 动态规划 Dynamic Programming

  

  一直去迭代这个bellman equation，直到他们函数$v(s)$收敛

• 蒙特卡罗方法 Monte-Carlo

  

  其实就是大量的模拟取平均，举个例子：

  

  对于$s_4$的价值，我们首先随机的生成一些路径，看看这些路径带来的价值，然后用获得的价值和除以路径数，就可以估算这个状态点可以获得的价值期望。

马尔科夫决策过程(Markov Decision Process,MDP)：

马尔科夫决策过程 = 马尔可夫奖励过程 + 决策(action)

此时，状态转移的概率分布也会收到action影响，那么reward function也会受到action影响。

而action是什么是取决于策略(policy)的，而policy有两种，分别是：deterministic和stochastic的。

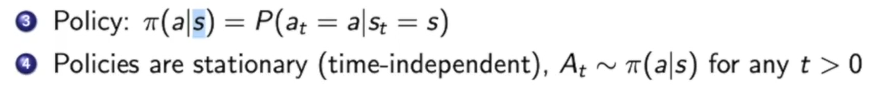
在这里我们有一个假设就是，各个时间点上都是在对policy function采样。

如果我们知道马尔可夫决策过程并已知采取的策略，那么我们就可以把马尔可夫决策过程转化为马尔科夫奖励过程。

马尔可夫奖励过程和马尔可夫决策过程的区别：

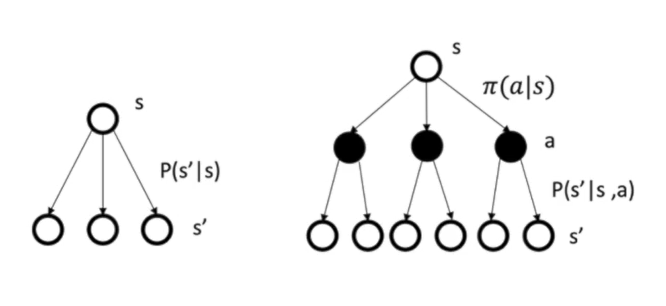
上图可以看出马尔可夫决策过程多了一个在某个状态下action的分布，这个action的不同会导致不同的状态转移矩阵。

在马尔可夫决策过程中：

对于一个状态价值函数$v^{\pi}(s)$，就是衡量在策略$\pi$下这个状态的价值。

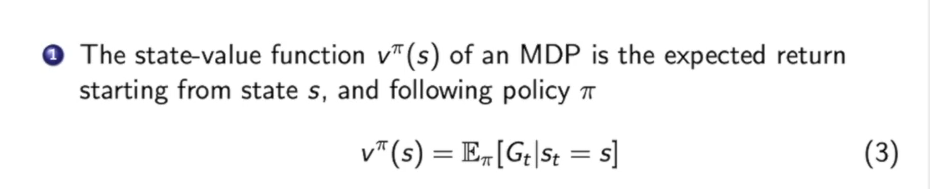
在马尔可夫决策过程过出现了一个新的动作价值函数(action-value function)，他表示在决策$\pi$下，状态$s$时，采取动作$a$，所获得的价值。

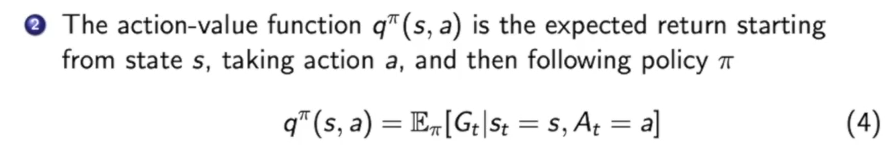
不难发现，$v^{\pi}(s)$和$q^{\pi}(s,a)$很相似，我们只需要让$q^{\pi}(s,a)$取到各种action，算一算期望，就可以得到$v^{\pi}(s)$。

因此：

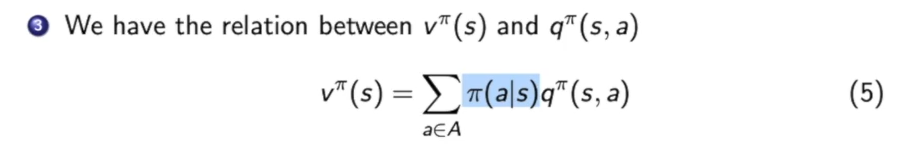
$\pi(a|s)$代表在状态$s$下做出动作$a$的概率。

Bellman Expectation Equation：

用当前状态和下一状态的方式 重写了 state-value function 和 action-value function。

上面我们提到了$v^{\pi}(s)$和$q^{\pi}(s,a)$的关系(即下式(8)),我们还有Bellman Expectation Equation(下式(9))，那么我们就可以推出(10),(11):

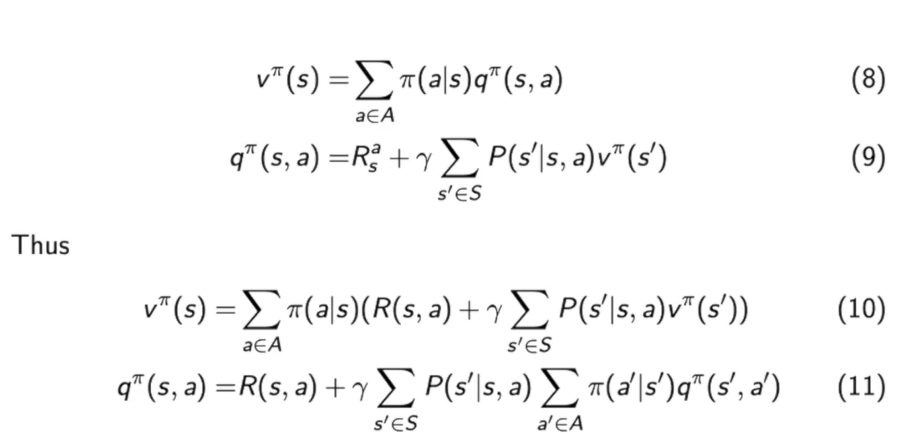
$v^{\pi}(s) =\sum{a \in A} \pi(a \mid s)\left(R(s, a)+\gamma \sum{s^{\prime} \in S} P\left(s^{\prime} \mid s, a\right) v^{\pi}\left(s^{\prime}\right)\right)$这个式子并不难理解，如下图：

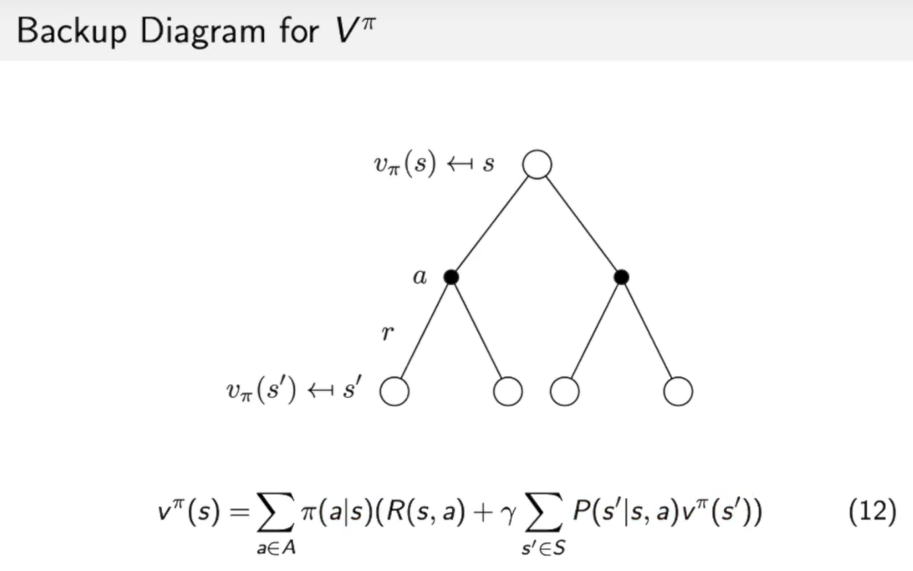
首先$R(s,a)+\gamma \Sigma_{s’ \in S}P(s’|s,a)v^{\pi}(s’)$代表在状态$s$，做出动作$a$，到达状态$s’$时的价值所得到的reward。也就是叶子节点backup到了黑色节点action，代表在这个动作下所获的reward，也就是$q^{\pi}(s,a)$。第二次backup就是action节点到根节点状态s，即：

$v^{\pi}(s)=\sum{a \in A} \pi(a \mid s)\left(R(s, a)+\gamma \sum{s^{\prime} \in S} P\left(s^{\prime} \mid s, a\right) v^{\pi}\left(s^{\prime}\right)\right)$

相当于对不同action的reward 乘上这个action在状态s下出现的几率，计算了在状态s获得价值的期望。

最后举一个例子：

马尔可夫链/马尔科夫奖励过程相当于小船随波逐流，到哪儿完全凭随机，没有任何主观的干扰(比如action)。而马尔可夫决策过程则完全不同，除了河流的流向影响着状态，船夫所做的行动也会影响船的走向。