强化学习纲要Ch4-无模型价值函数估计和控制-上

无模型的价值函数估计和控制—上

image-20210505200826789

这一次讲的是model-free的value function的预策(prediction)和控制(control)。

model-free就是指无模型，MDP不是已知的。也就是说我们不知道$R(Reward)$和状态转移矩阵$P$

下面是上一次课的concise review：

image-20210505201103886

对于Model-free的RL，我们没有了R和P, 因此我们需要从交互过程中来学习：

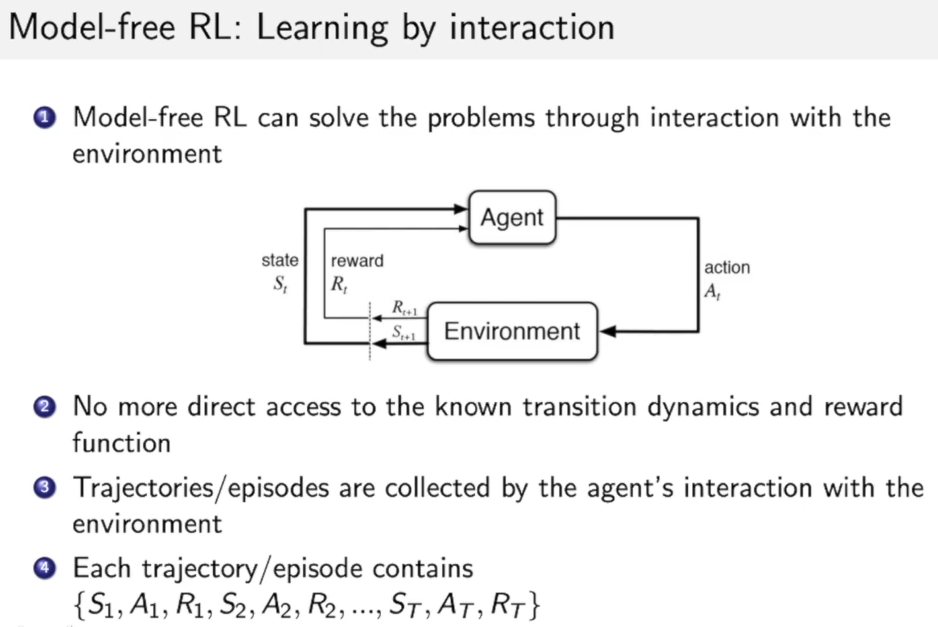
image-20210505203412074

而交互过程就是这样的一个序列：${S_1,A_1,R_1,S_2,A_2,R_2,..S_T,A_T,R_T}$

image-20210505204213590

在model-free时，如何在特定的策略下，估计状态的价值函数呢？

  • 蒙特卡洛策略估计

    image-20210505210813648

    为了写成迭代的形式，我们可以建立一个上一时刻的平均值和下一时刻平均值的关系：

    $\begin{aligned} \mu{t} &=\frac{1}{t} \sum{j=1}^{t} x{j} \ &=\frac{1}{t}\left(x{t}+\sum{j=1}^{t-1} x{j}\right) \ &=\frac{1}{t}\left(x{t}+(t-1) \mu{t-1}\right) \ &=\mu{t-1}+\frac{1}{t}\left(x{t}-\mu_{t-1}\right) \end{aligned}$

    利用这个方法，我们可以改写一下蒙特卡洛的方法：

    image-20210505211616960

    这里比较一下蒙特卡洛MC方法和动态规划DP方法的区别：

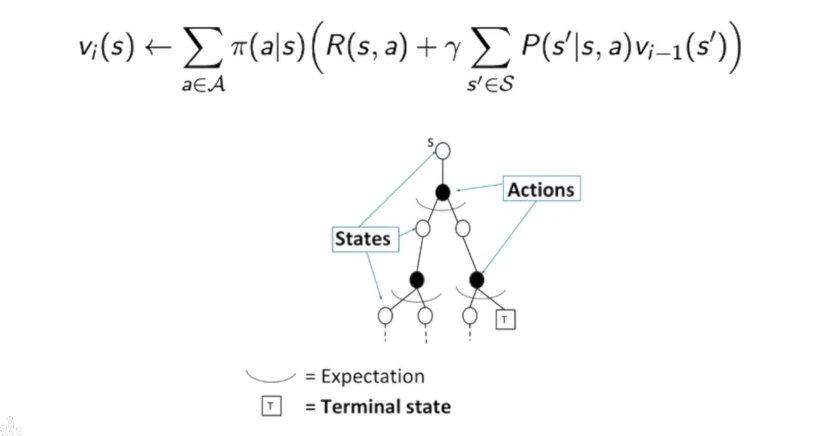
    image-20210505212157744

    在DP中，我们获得一个状态的价值是根据下层所有情况来得到的。

    而在MC中：

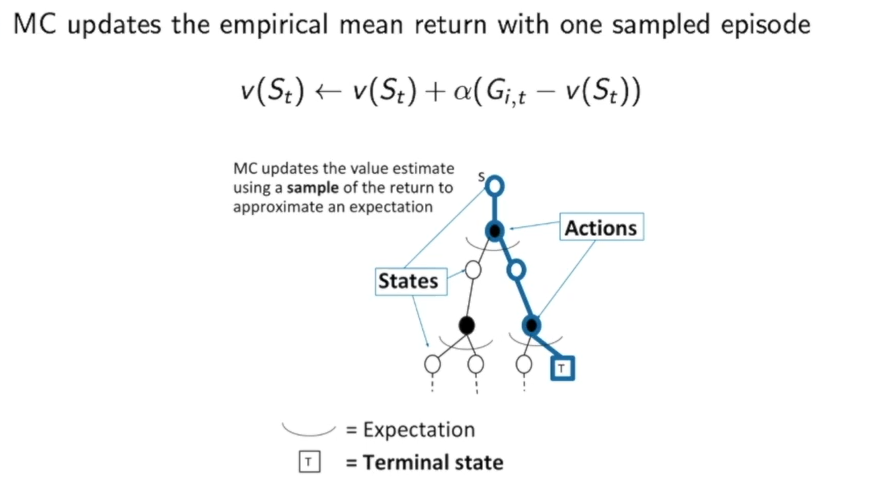
    image-20210505212302882

    我们只是根据几条路径来大致估计的，可能有些路径会被忽略掉，因此并不是根据下层所有可能出现的情况来得到状态的价值的。

    造成这样区别的主要原因就是：我们不知道状态转移概率矩阵P。

  • Temporal Difference(TD) learning ，时间差分学习

    image-20210505213619048

TD方法也是用了上面的一个online mean的技巧，这里它通过TD target（即$R{t+1}+\gamma v(S{t+1})$）来更新，这一步由两部分分别是$R{t+1}$和$\gamma v(S{t+1})$：

$R{t+1}$是在新的一步中直接获得的奖励，第二部分$\gamma v(S{t+1})$利用了动态规划的思想，利用之前的估计来估计现在的，也就是当前$St$可以转移到$S{t+1}$,那么就用$S_{t+1}$的value function的值来更新即可。

我们对比一下TD和 MC方法的区别：

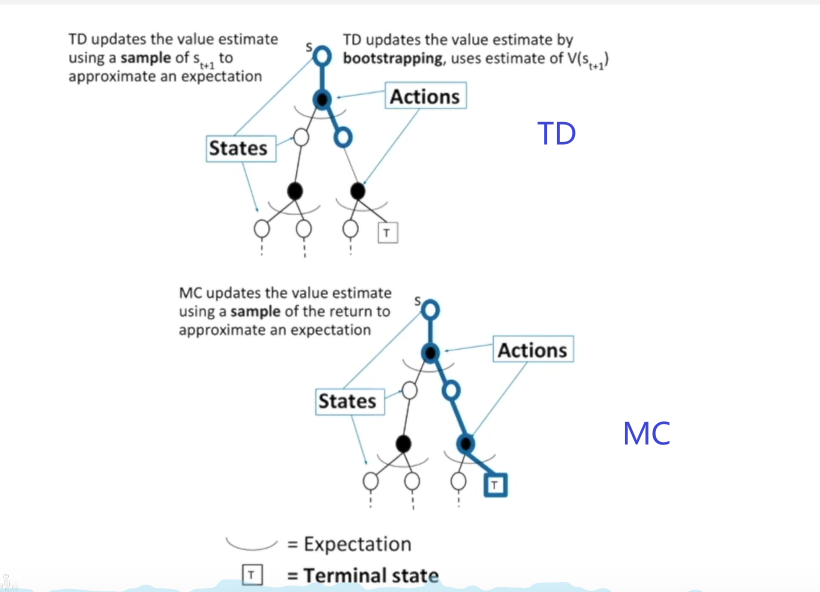
image-20210505215024640

更多的区别：

  1. TD算法在每一步状态的转移下都可以实时在线学习，而MC必须做完一个episode才能知道return的大小。
  2. TD可以从不完整的交互序列来学习，而MC不可以，他必须需要一个完整的交互序列才可以得到return
  3. TD可以在一个无终止的环境下学习，而MC由于需要完整的序列，而无终止环境下序列是无限长的，因此MC无法在无终止的环境下学习。
  4. 当然，TD也有缺点，就是TD假设了强化学习任务有马尔科夫特征，即当前状态只和上一时刻有关系，而与更早的时刻无关。而MC没有对马尔科夫环境做出要求。

TD有一些灵活的用法，比如n-step TD：

image-20210505215917166

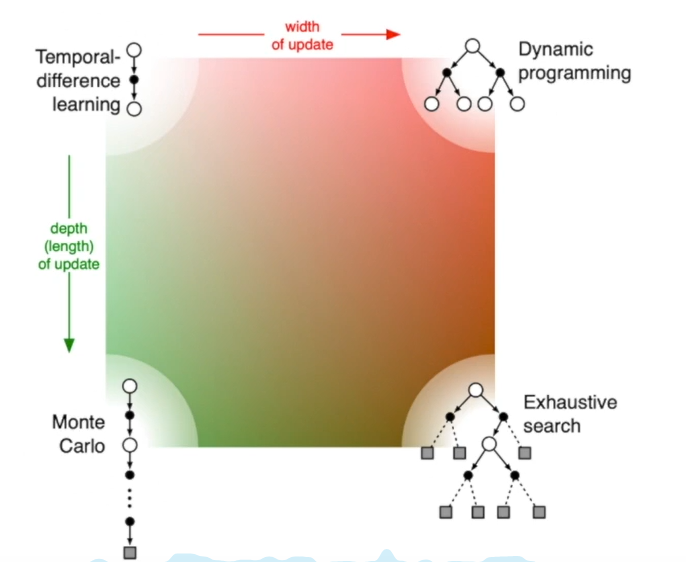
image-20210506085517428

TD的step如果远一些，那么就会加大搜索深度，到达极限即使MC方法，也就是找到一条完整的路径来算return。而TD加宽搜索广度即是DP方法。如果又宽又广即是穷举了决策树，也就是穷举算法。

image-20210506085849669

统计学中，bootstrapping可以指依赖于重置随机抽样的一切试验。bootstrapping可以用于计算样本估计的准确性。对于一个采样，我们只能计算出某个统计量统计量)(例如均值))的一个取值，无法知道均值统计量的分布情况。但是通过自助法(bootstrapping)我们可以模拟出均值统计量的近似分布。有了分布很多事情就可以做了（比如说有你推出的结果来进而推测实际总体的情况）。

在这里我们可以简单理解为在估计上估计(estimate by estimating)，比如DP就用到了这种思想，利用了其他状态的value function的值来估计一个状态value function的值。

而MC没有，他是抽取了决策树的一部分的支路，然后取了个平均，每一步都是实实在在的return，没有任何估计，因此是estimate by sampling。

而在TD中由于TD target包含两部分：$R{t+1}$和$\gamma v(S{t+1})$

$R{t+1}$是通过真实的走一步，看看得到了环境的return是什么，因此这是sample，而后面的$\gamma v(S{t+1})$就是利用了bootstrap。