强化学习纲要Ch10-策略优化进阶
策略优化进阶——上
本次的内容:

首先还是先回顾一下Value-based RL和Policy-based RL区别:

策略目标和策略梯度:
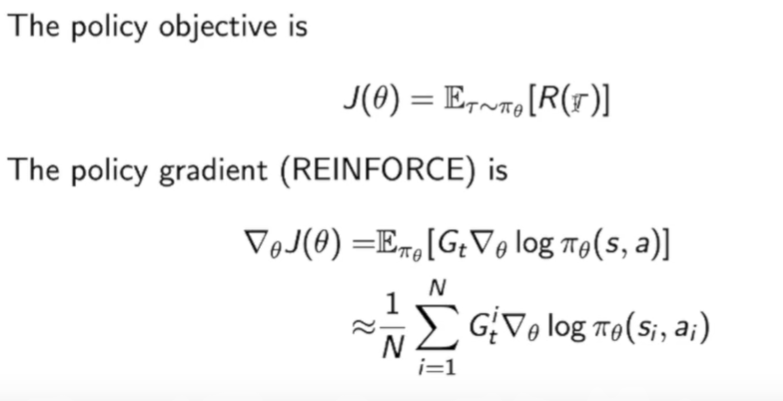
策略梯度(Policy gradient)有下面几种常见的算法:

这里要说一下这四个优化方法的关系:
首先是REINFORCE使用的是$G_t$,是由MC方法获得的,他其实就是Q Actor-Critic方法中$Q^w$的采样。Advantage Actor-Critic中为$A^w$,即把$Q^w$减去了一个baseline,这么做是为了减少方差。TD Acrot-critic中直接使用TD target作为reward function。
critic会用policy evaluation来估计$Q^\pi(s,a)$,$A^\pi(s,a)$,$V^\pi(s)$
下面介绍当下最历害/前沿的六种强化学习算法:

TRPO
在介绍这些算法前,首先我们要了解基于Policy Gradient的缺点:
- 首先是sample effiency问题:当前优化的policy不仅要被优化,也要用这个policy来采取数据,所以采样效率其实很低。
- 训练过程不稳定:强化学习采集到的数据一般都不是iid的,有很强的关联。比如我们的step size不是那么正确,导致的结果是:step too far->bad policy->bad data,也就是坏的策略会导致坏的数据,坏的数据会使得策略变得更差,导致我们很难从一个错误的policy中恢复回来。
对应于这两点,解决方法是:
怎么让训练更稳定:利用Trust region和natual policy gradient
怎么让sample高效一些:用另一个policy去产生策略,即off-policy方法,比如在TPRO中就用到了Importance sampling
Natural Policy gradient的概念:

原来我们考虑的policy gradient就是在一个欧几里得空间找一个d,这个d方向可以使得$J(\theta)$变化最快。
但是这里有个问题就是,这个d对采取怎样参数化的形式很敏感。
所以这里提出了一种新的方法:通过分布空间(policy output)来进行梯度更新

利用KL散度控制梯度变化前后的输出的分布的差异为一个定值c,然后在此基础上在参数空间中找一个d使得J函数变换最大。
这里补充一下KL散度的概念:

上面说到,我们现在考虑得更新方式为:

这种constraint的最优化可以用拉格朗日乘子来解决,如上图。然后把KL[]这个函数用泰勒展开,得到上图中的式子。
然后我们对上面那个优化函数求导即可,就可以得到natual policy gradient:

因此我们现在策略的更新方式为:

和原来相比就是多了一个$F^{-1}$,即Fisher information matrix。

这里的F就是KL散度的二阶导数,我们可以用下式进行计算。
$F=E{ \left.\pi{\theta}(s, a}\right]}\left[\nabla \log \pi{\theta}(s, a) \nabla \log \pi{\theta}(s, a)^{T}\right]$
F意味着策略的曲率与模型参数$\theta$的相关性。
所以Natural policy gradient的出现使得我们让策略优化可以与模型参数空间的选择无关。
Importance Sampling方法:
另外一个方面是我们想把policy gradient方法改成off-policy的方法,我们知道off-policy learning自身有很多好处,我们可以用另一种算法在环境里面去探索(explore),采集到很多激进的数据,这样来喂给优化的策略。
这里采取方法是Importance sampling(重要性采样):Importance sampling在采样过程里面也是用的比较广泛的。
它的简单概念是:我们现在假设要去估计一个函数的期望,比如说要估算f(x)这个值,x是从p分布里面采样出来的;有时候我们不知道怎么去p分布里面采样,比如说p分布的形式非常奇怪,没法去直接采样,我们只能从如uniform distribution或者Gaussian distribution里面采样,那么我们怎么去根据一个不知道怎么采样的p估计这个f(x)参数呢?
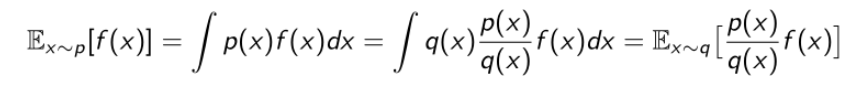
通过简单的变换,f(x)针对p的期望,变换成另一种期望的形式,这样x就可以从另外一个分布里面采样了。采样很多的x后再取平均。
同样的原理,我们可以把策略优化的目标函数也改写一下:
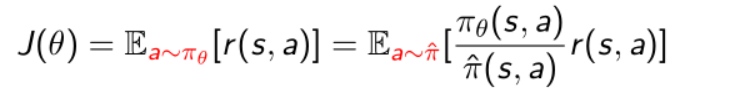
α是优化的策略里面产生的,假设我们现在优化函数没法对它采样,就可以从另外一个策略函数里面对它采样,比如从 $\hat{\pi}$里面去采样action,通过importance sampling去乘以ratio来近似。这里变化就是我们可以用behavior policy $ \hat{\pi}$ 去产生实际的轨迹。
Increasing the Robustness(鲁棒性) with Trust Regions(信赖域):
所以这样就可以把策略函数改写成基于之前另外一个策略的一个优化函数,另外一个策略最简单的办法是可以用之前的这个策略,在Deep Q learning中有两个策略函数,behavior policy是用的之前的策略函数,因为之前的策略函数产生的数据我们也可以放到这个replay buffer里面,所以就可以重用之前采到的数据。
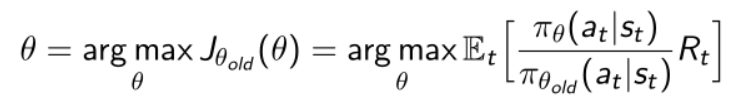
这里有个问题需要注意一下,$\frac{\pi_\theta}{\hat{\pi}}$可能非常大,也就是说上下两个策略差距比较大,同样我们可以借用上面的方法,用KL散度来限制分布的差异,限制两个策略的区别:

一个形象的例子是:

每次优化过程只能在这个圆圈里面(安全的区域)选择一个方向,这样就可以使得这个训练尽可能的稳定,这样也使得它的概率输出和上一步的概率输出的步数尽可能的小,随着训练过程也可以使得trust region缩的越来越小,更新也会变得越来越小,整个过程也会变得越来越稳定。
Trust Region Optimization:
对Trust Region Optimization进行进一步的推导,对价值函数做泰勒展开,展开如下:
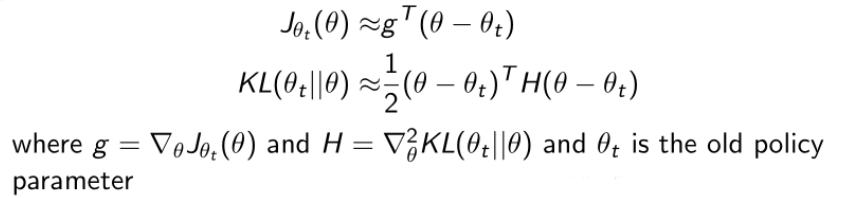
此时的目标变为:
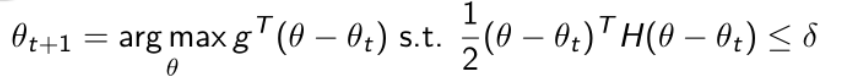
这个式子是有显示解的:
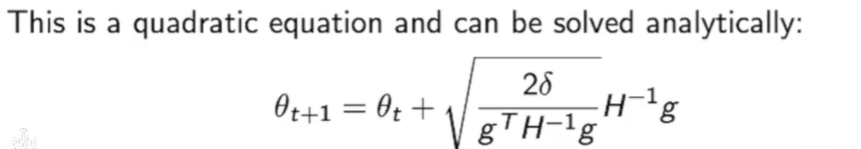
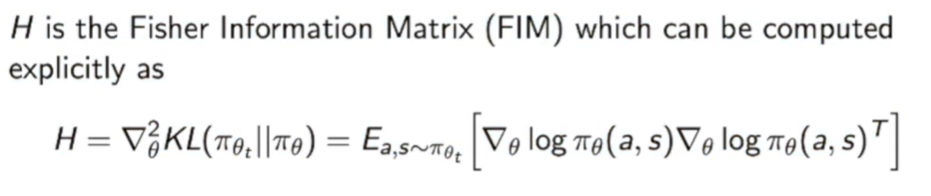
我们会发现他和Natural gradient(自然梯度)的形式很一致。
我们发现这个natural gradient没有学习率,而是用KL散度之间的差别$\delta$来代替学习率。δ是直接在限制更新之后的policy和之前的policy的近似程度 ,也就是说做了这个推导过后δ和learning rate直接联系起来了。这也是TRPO推导非常好的地方,不需要设定step-size,只需要指定trust region的大小,即更新后的策略和之前的策略输出距离多少,然后用距离去推出step-size。这样我们可以把trust region设的很小,这样就使得更新非常稳定。
到现在为止,我们推导的就是在TRPO中的Natural policy gradient:
- TRPO是在natural policy gradient的基础上加了importance sampling。

由于我们提到了H的逆这个问题,求逆复杂度是$O(n^3)$的,十分慢,因此我们常用共轭梯度法来解绝这个问题:

所以完整的方法就是:

TPRO中通过一些推导(具体可看论文的附录),证明了一个guaranteed monotonic improvement,即:
随着迭代增加,我们的J函数是单调的。

TPRO的一些问题:
- 计算量非常大。虽然用了conjugate gradient method(共轭梯度法),但是对于每一次迭代,policy都要算H逆。
- 在近似H的时候,H本身是个期望,但是我们在近似这个期望的时候是用样本近似,需要很多样本。

- TRPO在某些游戏上并不会比DQN更好。
ACKTR
paper: Y.Wu, et al. “Scalable trust-region method for deep reinforcement learning using Kronecker-factored approximation”. NIPS 2017.
ACKTR的核心思想是想提升TRPO的计算效率。在TRPO里面有一步是算Fisher information matrix(FIM),即$H^{-1}$,在矩阵维度很大的时候求逆计算量非常大。因此,ACKTR提出用Kronecker-factored approximation curvature(K-FAC) 方法来加速求逆。
PPO
PPO可以看作是TRPO的简单版本:
首先回顾TRPO的loss function:

我们采用这种方法区合并约束:

这样在优化时,一方面就考虑到了让前面一部分变大,另一方面让后面一部分变小。
我们会发现有个参数$\beta$在衡量他们二者,这个$\beta$可以做到自适应,如下的算法流程图:
当我们的KL散度过大,说明策略更新过快,变化过大,那么我们就变大$\beta$,让优化时更注重KL散度。反之亦然。
这个方法叫做PPO with Adaptive KL Penalty

因为PPO本身优化的过程是利用first-order optimization(SGD,一阶优化) 优化的,所以优化效率比二阶的TRPO快很多,因为PPO的算法过程中并没有去计算KL散度或者Fisher information matrix。
除了上面adaptive beta的方法,PPO提供了第二种方式是把objective function自身带了clipping,所以它提出了更复杂一些的形式来处理本身loss的优化情况。
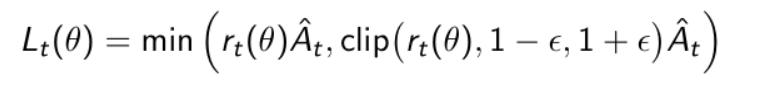

这就是PPO with Clipped Objective

本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!