强化学习纲要Ch9-策略优化基础-下

策略优化基础——下

Score Function Gradient Estimator

我们考虑写一个更广义的策略函数：

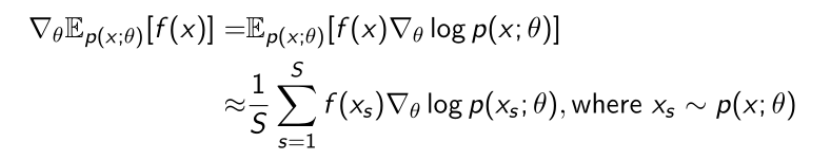
上面那个推导过程不太详细，下面给出具体的推导步骤：

这个梯度可以理解为：

p(x)为采样得到的值，他们梯度就是上图蓝色箭头，而f(x)代表给这些梯度一个权重。

比如当权重分布如下时：

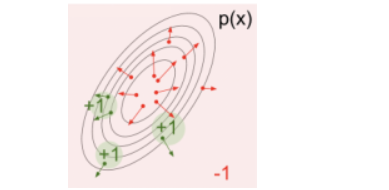
此时这个p(x)分布会向权值大的哪个方向平移，最后移动至下图：

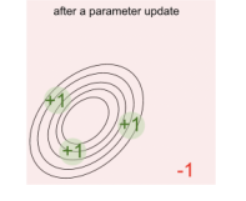
可以看到概率函数p(x)的形状变了，整个形状变得往能得到更高分数的区域走；所以score function gradient estimator就可以通过这样一个几何解释来理解。

Score Function Gradient Estimator与Maximum Likelihood estimator(极大似然估计)的对比：

score Function Gradient Estimator多了reward function，可以看成加权后的极大似然估计，也就是说这种policy gradient estimator鼓励函数向获得奖励更多的地方移动。

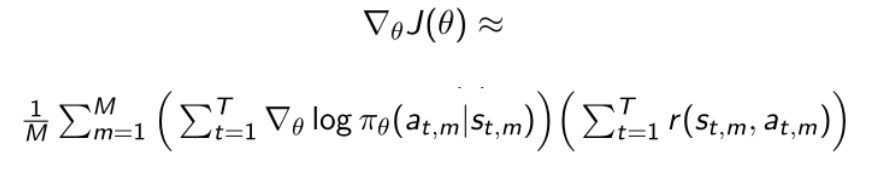
而极大似然估计就是单纯的优化一个参数，这个参数是从训练数据中学到的，他学到的是训练数据的分布。

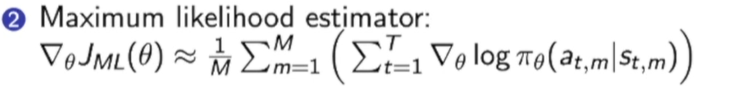
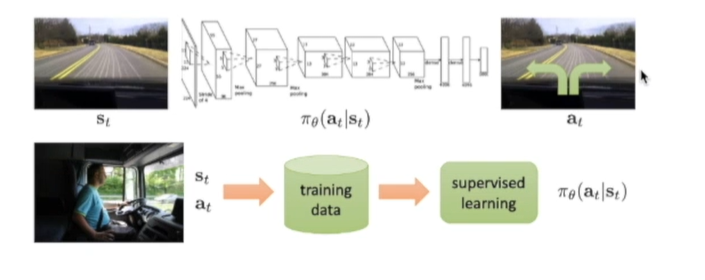
在优化的过程中，score Function Gradient Estimator这种policy gradient estimator方法是：鼓励策略进入到得到奖励尽可能多的区域里面。supervised learning是直接有个标签去优化函数；策略函数是优化策略概率函数使得能够尽可能进入到能够采样产生更高奖励的区域里面。

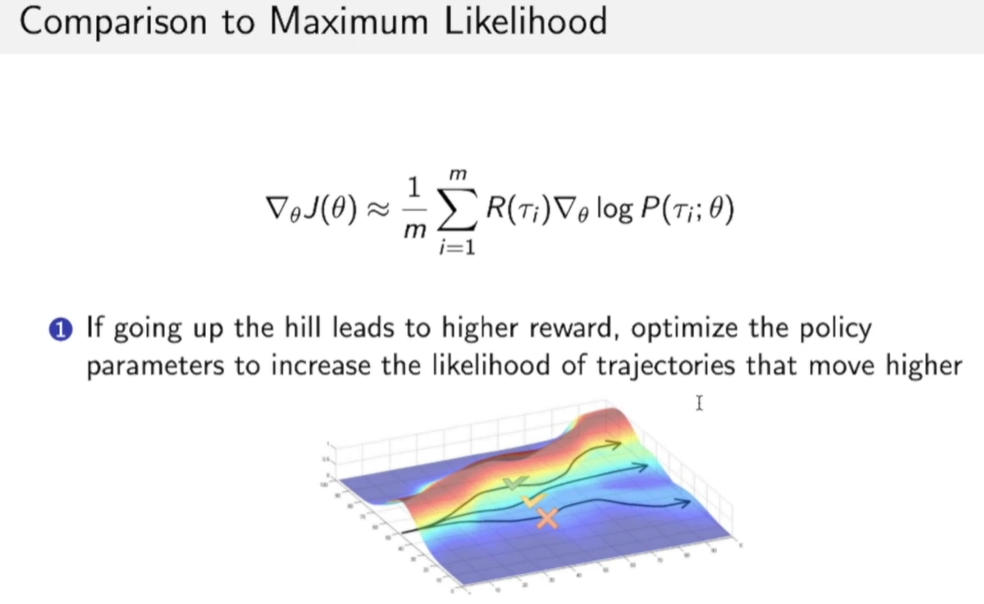
更形象的理解就是：

policy gradient方法希望优化概率分布函数$P$的参数$\theta$，从而使得函数更靠近获得奖励高的区域，如下图，我们其实就是希望P函数移动到靠近红色的区域上，这样我们采样时得到的奖励的期望也会更多。

Large Variance of Policy Gradient

现在policy gradient是采样产生的:

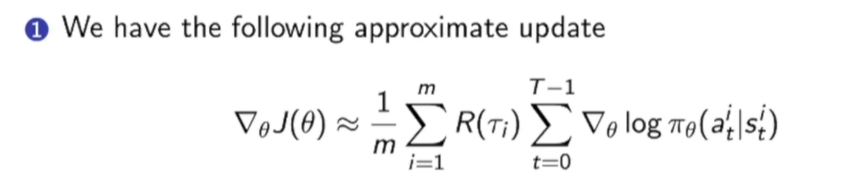
由于我们用的MC方法，即基于抽样得到的gradient。但是方差（variance)是非常大的，导致训练不稳定，因此我们现在的新的目标就是减少方差。

有两种办法减少Policy Gradient的方差：

方法一：Use temporal causality利用时序上的因果关系减少variance

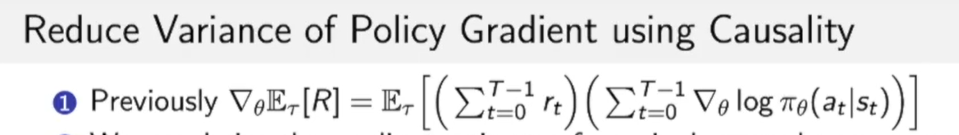
原来这个式子有一个问题就是，这个式子没有因果关系，他先计算了路径上的log likelihood，然后再把路径上每个点的奖励进行加和。

不如写成如下形式：我们每走一步，只计算当前一步所获得奖励。

即写为下式：

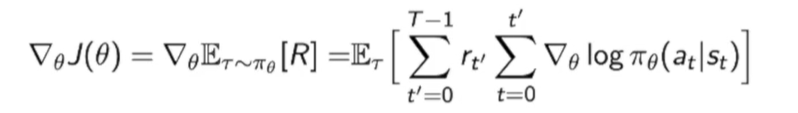
那我们的原来的梯度就可以改写成：

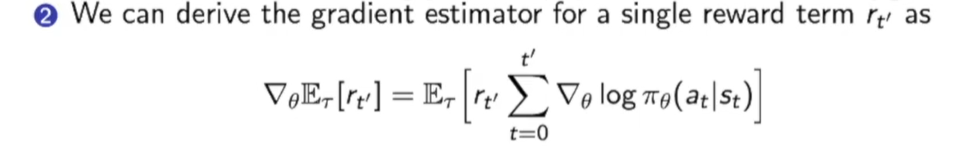
进行一点推到：

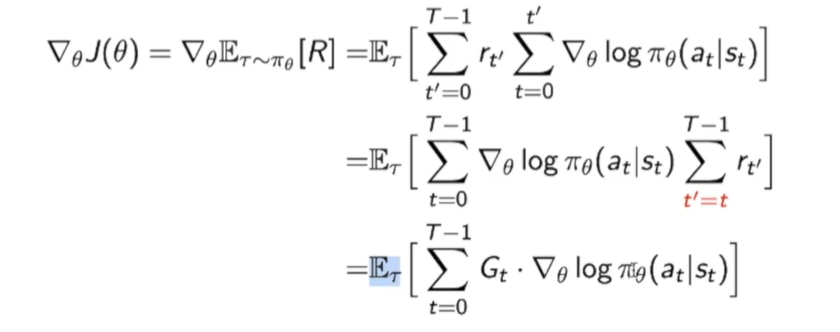
最后的$Gt=\sum{t^{\prime}=t}^{T-1} r_{t^{\prime}}$

说一些推到中的细节：

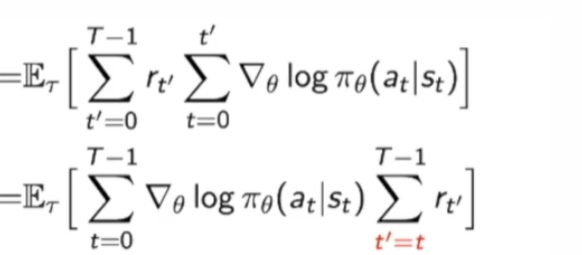
这一步的转化就是和算贡献一样：前面时刻t的每一个score function会对后面时刻的$r_{t’}$做贡献,其中$t’>=t$

这个其实就是REINFORCE算法：

方法二：引入baseline

这个方法可以不改变期望(保证了仍然是无偏估计)的同时还降低方差：

期望为0的证明：

Vanilla Policy Gradient Algorithm with Baseline：

有时候我们会把baseline用一种参数去拟合，写为$b_w(s)$
使得baseline本身带有参数w，在优化过程中同时优化 $\theta$和$w$。

对于每次迭代:iter = 1,2,....：
	用策略\pi_theta收集m条轨迹
	对于每个轨迹\tau的每一步t：
		计算G_t^(i)=r_{t}+r_{t+1}+...r_{T-1}
		计算advantage estimate：A_t^(i) = G_t^(i)-b(s_t)
	通过更新w来更新b(s_t)，即最小化(b(s_t)-G_t^(i))^2：
	计算策略梯度g
	利用SGD/Adam更新参数\theta
return /theta，baseline(即b(s))

Actor-critic

我们在上一小节已经提出了Policy gradient：

我们会用一种新的方法来减少梯度，这种方法就是利用cirtic（评价者）

首先$G_t$在前面提到过是在MC 梯度下降中抽样而来，它本质上是对Q函数无偏的估计：

我们这里利用critic去估计Q函数从而替换掉$G_t$:

那么这就是Actor-Critic Policy Gradient方法：

Actor表演者：它就是利用策略函数生成动作，因此成为actor.

Critic评价者：评价这个动作的价值，类似于Q函数。

这个critic和policy evaluation的作用很类似：评价当前策略$\pi_\theta$的参数$\theta$到底好不好。

计算方法有以下三种：

这样我们就得到了QAC算法：

假设critic是一个线性的价值函数：

QAC算法流程图：

这里利用TD error来更新w，由于我们假设了critic的$Q_w$由$\psi$的线性组合得到，那么$Q_w$的梯度就是$\psi$ ，因此更新w的式子为：$\mathbf{w} \leftarrow \mathbf{w}+\beta \delta \psi(s, a)$

而$\theta$得更新就是policy gradient更新即可。

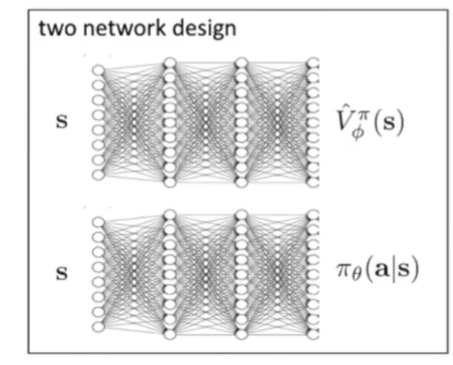
理论上我们需要用两个不同的函数来拟合：

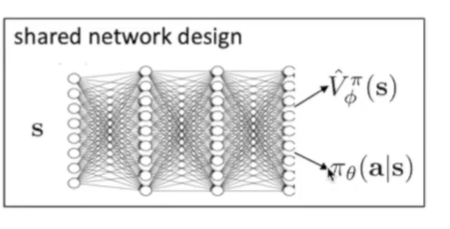
实际中我们可以让这两个函数共享网络结构，节省计算：

Actor-critic这种方法同样可以用baseline来减少方差：

首先回顾一下Q函数和V函数：

我们之前定义的baseline是：

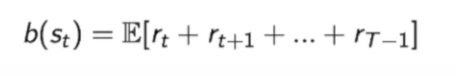
因为$Gt=r_t+r{t+1}+…r_{T-1}$

因此:$b(s_t)= E(G_t)$

而我们之前提到过用Q函数代替$G_t$,那么$b(s_t)=E(Q(.))=V^{\pi,\gamma}(s)$

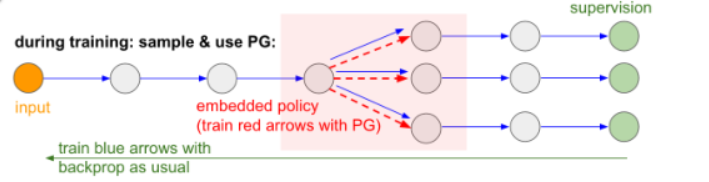
policy gradient的一个非常好的应用：解决不可微分的计算成分

比如一个网络的得传播是由多段组成的：

中间可能有一段是不可维分的，那么对于这样一部分会使得我们在bp时无法传播到前半段。

解决方法有两个：

方法一：用Reparameterization trick(VAE变分编码器中使用的trick)的方法。（不懂，以后再说QAQ）
方法二：用采样的方法，中间不可微的阶段可以用样本来替代。

基于policy gradient的算法有很多：

RL的两个学派：

1.Value-based RL:利用dynamic programming和bootstrapping的方法去优化它的价值函数，得到价值函数后，从Q函数里面采取行为。
代表算法：Deep Q-learning and its variant
代表人物：Richard Sutton (no more than 20 pages on PG out of the 500-page textbook), David Silver, from DeepMind
从控制论背景出发
2.Policy-based RL:只需要少量样本，就可以拟合出策略函数。
代表算法： PG, and its variants TRPO, PPO, and others
代表人物：Pieter Abbeel, Sergey Levine, John
Schulman, from OpenAI, Berkelely
从机器人，机器学习背景出发

DeepMind和OpenAI两大RL流派区别：
https://www.zhihu.com/question/316626294/answer/627373838
殊途同归，都往Actor-critic发展。
DeepMind主要研究游戏领域，主要跑仿真对样本本身不挑剔；OpenAI研究机器人，更注重sample effectioncy（有效性），减少采样。

强化学习

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议，转载请注明出处！

强化学习纲要Ch10-策略优化进阶上一篇

机器学习中的KernelModel/LinearModel总结下一篇