LeetCode 建信 04.电学实验课(矩阵快速幂，计数)

LeetCode 建信 04.电学实验课(矩阵快速幂，计数)

题目描述:

某电学实验使用了 row * col 个插孔的面包板，可视作二维矩阵，左上角记作 (0,0)。老师设置了若干「目标插孔」，它们位置对应的矩阵下标记于二维数组 position。实验目标要求同学们用导线连接所有「目标插孔」，即从任意一个「目标插孔」沿导线可以到达其他任意「目标插孔」。受实验导线长度所限，导线的连接规则如下：

一条导线可连接 相邻两列 的且 行间距 不超过 1 的两个插孔
每一列插孔中最多使用其中一个插孔（包括「目标插孔」）
若实验目标可达成，请返回使用导线数量最少的连接所有目标插孔的方案数；否则请返回 0。

注意:
输入数据保证每列最多仅有一个「目标插孔」；
答案需要以 1e9 + 7 (1000000007) 为底取模，如：计算初始结果为：1000000008，请返回 1。

样例

输入：row = 5, col = 6, position = [[1,3],[3,2],[4,1]]
输出：0
解释：根据连接规则无法达成实验目标。

image-20211110160849593

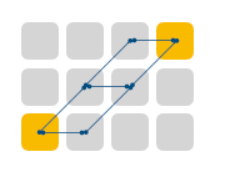
输入：row = 3，col = 4, position = [[0,3],[2,0]]
输出：3
解释：根据连接规则共有三种方案达成目标。

image-20211110160915463

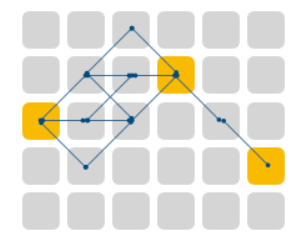
输入：row = 5, col = 6, position = [[1,3],[3,5],[2,0]]
输出：6
解释：根据连接规则共有六种方案达成目标。

image-20211110160939693

限制

$1 <= row <= 20\
3 <= col <= 10^9\
1 < position.length <= 1000\
0 <= position[i][0] < row\
0 <= position[i][1] < col$

思路

​ 由于每列只有一个插孔，所以连接顺序一定是从左到右一次连接，不会出现折返(这违反了”每一列插孔中最多使用其中一个插孔（包括「目标插孔」）”这个条件)。且每次前进一列一定只有三种连接方式：右上，右，右下。

​ 将目标插孔按照列的大小排序，然后计算$position[i][1]$ 到$posistion[i-1][1]$两个相邻目标插孔间的方案数即可，最终答案就是 将这些相邻目标插孔方案数连乘起来。

​ 考虑如何计算相邻目标插孔的方案数？我们先考虑相邻两列之间有哪儿些行可以转移，不妨设一个转移矩阵$T$，$T[i][j]$就代表当前一列的第$i$行可以转移到当前列的第$j$行。这个计算很简单：

1
2
3
4
5
6
7
8
t[0].len = row;
for(int i=0;i<row;i++)
{
    for(int j=max(i-1,0);j<=min(i+1,row-1);j++)
    {
        t[0].a[i][j] = 1;
    }
}

​ 但是目标插孔相邻两列之间的距离不一定是1，加入是2，那么令$T=T^2$,此时$T[i][j]$就代表了前两列的第$i$行到当前第$j$行的方案数。可以列的范围高达1e9，如果目标插孔相邻两列之间的距离为1e9那怎么办呢？直接$T^{1e9}$这是不合理的复杂度高达$O(n^3m)$, 考虑矩阵快速幂，对1e9进行二进制拆分即可。我们只需要预处理出$T,T^2,T^4,T^8….T^{2^{30}}$即可，每次只需要前一个平方即可递推出下一个，预处理复杂度是$O(30*n^3)$。

​ 接下来逐一处理相邻两个目标插孔即可，d二进制拆分$logd$，每次$n^3$的复杂度的矩阵乘法。最后复杂度是$O(nlogmn^3)$。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
typedef long long ll;
const int MAXN = 1e6+10;
const int INF = 0x3f3f3f3f;
const ll MOD = 1e9+7;

class Solution {
public:
    int r,c;

    struct M{
        ll a[20][20];
        int len;
        M(){
            memset(a,0,sizeof a);
        }
    };
    bool cmp(vector<int>x,vector<int>y)
    {
        return x[1]<y[1];
    }
    M operator *(const M &x,const M &y)
    {
        M ans;
        for(int i=0;i<x.len;i++)
        {
            for(int j=0;j<x.len;j++)
            {
                for(int k=0;k<x.len;k++)
                {
                    ans.a[i][j] = (ans.a[i][j] + (x.a[i][k]*y.a[k][j])%MOD)%MOD;
                }
            }
        }
        ans.len = x.len;
        return z;
    }
    int electricityExperiment(int row, int col, vector<vector<int>>& p) {
        r = row, c = col;
        M t[33];
        t[0].len = row;
        for(int i=0;i<row;i++)
        {
            for(int j=max(i-1,0);j<=min(i+1,row-1);j++)
            {
                t[0].a[i][j] = 1;
            }
        }
        for(int i=1;i<30;i++)
        {
            t[i] = t[i-1] * t[i-1];
        }
        ll ans = 0;
        sort(p.begin(),p.end(),cmp);
        for(int i=1;i<p.size();i++)
        {
            M tep;
            tep.len = row;
            int d = p[i][1] - p[i-1][1];
            for(int j=0;j<row;j++)
            {
                tep.a[j][j] = 1;
            }
            for (int j = 0; j < 30; j++)
            {
                if (y & (1 << j)) tep = tep * t[j];
            }
            ans = ans*tep.a[p[i-1][0]][p[i][0]]%MOD;
            if(ans==0) return ans;
        }
        return ans;
    }
};