比赛板子

一切的开始

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include<bits/stdc++.h>
using namespace std;
#define pii pair<int,int>
#define pll pair<ll,ll>
#define pdd pair<double,double>
#define fastIO ios::sync_with_stdio(false);cin.tie(0);
#define endl "\n"
typedef long long ll;
const int INF=0x3f3f3f3f;
const int MAXN=5e5+7;
const long long MOD=998244353;
const double pi=acos(-1);
const double eps=1e-4;
vector<int>di = {-1, 1, 0, 0}, dj = {0, 0, -1, 1};

int main()
{
    fastIO

    
    return 0;
}

基础

离散化

1
2
3
4
5
6
7
int C[MAXN], L[MAXN];
// 在main函数中...
memcpy(C, A, sizeof(A)); // 复制
sort(C, C + n); // 排序
int l = unique(C, C + n) - C; // 去重
for (int i = 0; i < n; ++i)
    L[i] = lower_bound(C, C + l, A[i]) - C + 1; // 查找

三分

1
2
3
4
5
6
7
8
9
while (r - l > eps)
{
    mid = (l + r) / 2;
    double fl = f(mid - eps), fr = f(mid + eps);
    if (fl < fr)
        l = mid; // 这里不写成mid - eps，防止死循环；可能会错过极值，但在误差范围以内所以没关系
    else
        r = mid;
}

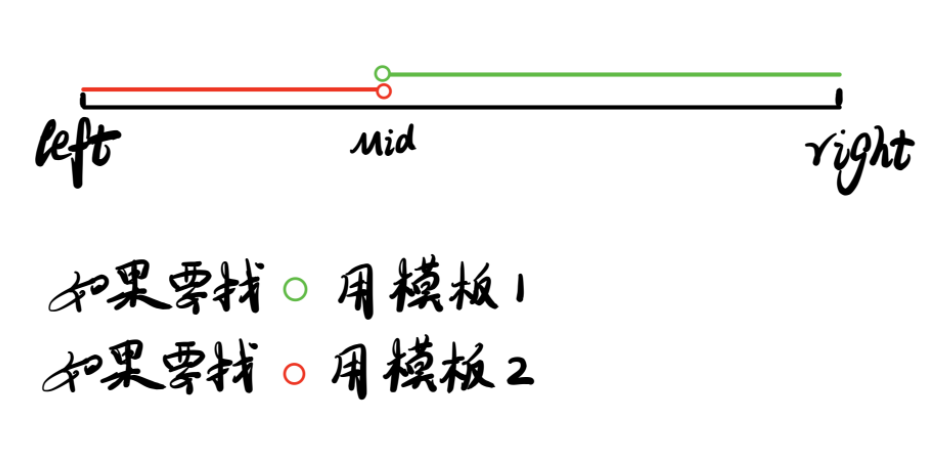
二分

整数集合上的二分：

image-20210117220854401

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
// 判断条件很复杂时用check函数，否则if后直接写条件即可
bool check(int mid) {
    ...
    return ...;
}

// 能二分的题一定是满足某种性质，分成左右两部分
// if的判断条件是让mid落在满足你想要结果的区间内

// 找满足某个条件的第一个数  即右半段
int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;  
        else l = mid + 1;
    }
    return l;
}

// 找满足某个条件的最后一个数  即左半段
int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

实数域上的二分：

$eps=10^{-(k+2)}$ $k=保留小数k位$

1
2
3
4
5
6
7
8
9
10
11
12
13
bool check(double x) {/* ... */} // 检查x是否满足某种性质

double bsearch_3(double l, double r)
{
    const double eps = 1e-6;   // eps 表示精度，取决于题目对精度的要求
    while (r - l > eps)
    {
        double mid = (l + r) / 2;
        if (check(mid)) r = mid;
        else l = mid;
    }
    return l;
}

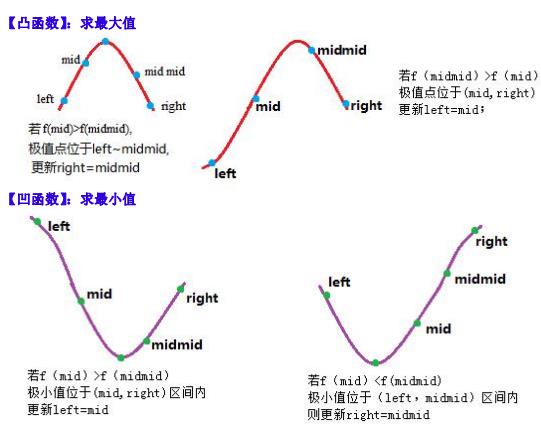
实数域上的三分：

360截图20191113165558620.jpg

1
2
3
4
5
6
7
8
9
10
11
12
13
double f(double a){/*根据题目意思计算*/}
double three(double l,double r) //找凸点
{
    while(l<r-1)
    {
        double mid=(l+r)/2;
        double mmid=(mid+r)/2;
        if(f(mid)>f(mmid)) r=mmid;
        else l=mid;
    }
    if(f(l)>f(r)) return l;
    else return r;
}

数学

整除分块

1
2
3
4
5
6
7
8
9
int ans = 0;
int k = 10;
for(int l=1,r;l<=k;l=r+1)
{
    if(k / l != 0)
        r=k / (k / l);
    else r = k;
    ans += (k / l) * (r - l + 1);
}

这里和上一个模板的改变是：将连续的$\lfloor 10/i\rfloor$数值相等区间前的系数$i$ 用等差数列求和快速求出。相当于每一段多了一个系数。

1
2
3
4
5
6
7
8
9
int ans = 0;
int k = 10;
for(int l=1,r;l<=k;l=r+1)
{
    if(k / l != 0)
        r=k / (k / l);
    else r = k;
    ans += (k / l) * (r - l + 1)*(l + r) / 2;
}

上下取整的转换技巧

上取整函数建议自己写 ：

1
2
3
4
5
6
7
8
//方法1：
if (temp%k == 0)
    result = temp / k ;
else
    result = (temp / k)+1;

//方法2：但要注意temp+k是否有可能溢出
result = (temp +k-1)/ k;

转换技巧: 有时候需要我们做整除分块，将上整除转换为下整除

Lucas定理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
ll  n, m, p;
ll Ext_gcd(ll a, ll b, ll &x, ll &y) 
{
	if (b == 0) { x = 1, y = 0; return a; }
	ll ret = Ext_gcd(b, a%b, y, x);
	y -= a / b * x;
	return ret;
}
ll Inv(ll a, int m) 
{   
	ll d, x, y, t = (ll)m;
	d = Ext_gcd(a, t, x, y);
	if (d == 1) return (x%t + t) % t;
	return -1;
}
 
ll Cm(ll n, ll m, ll p)  
{
	ll a = 1, b = 1;
	if (m > n) return 0;
	while (m)
	{
		a = (a*n) % p;
		b = (b*m) % p;
		m--;
		n--;
	}
	return (ll)a*Inv(b, p) % p;  
}
 
int Lucas(ll n, ll m, ll p)  
{
	if (m == 0) return 1;
	return (ll)Cm(n%p, m%p, p)*(ll)Lucas(n / p, m / p, p) % p;
}
 
int main()
{
	int  T;
	cin >> T;
	while (T--)
	{
		scanf("%lld%lld%lld", &n, &m, &p);
		printf("%d\n", Lucas(n, m, p));
	}
	return 0;
}

lcm/gcd

1
2
3
4
5
6
7
8
9
ll gcd(ll a,ll b)
{
    return b==0?a:gcd(b,a%b);
}
 
ll lcm(ll a,ll b)
{
    return a*(b/gcd(a,b));
}

预处理阶乘+排列组合+逆元(预处理逆元)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
ll fac[MAXN];
ll facinv[MAXN];


//复杂度log2(x)
ll ksm(ll n,ll x,ll p=MOD)//n^x%p
{
    ll ans=1;
    ans=ans%p;
    while(x)
    {
        if(x&1) ans=ans*1ll*n%p;//1ll防止溢出
        n=n*1ll*n%p;
        x>>=1;
    }
    return ans;
}

void cal(ll range)
{
    fac[0] = 1;
    ll ans = 1;
    for(ll i=1;i<=range;i++) {ans = (ans*1ll*i)%MOD;fac[i] = ans;}
    facinv[range] = ksm(fac[range],MOD-2,MOD);
    for(ll i=range-1;i>=0;i--) {facinv[i] = facinv[i+1]*(i+1)%MOD;}
}

ll ccc(ll x,ll y)
{
    ll ans = fac[x];
    ans = (ans*facinv[y]%MOD)*facinv[x-y]%MOD;
    return ans;
}

ll aaa(ll x,ll y)
{
    ll ans = 1;
    for(ll i=1;i<=y;i++)
    {
        ans=ans*(1ll*y+1ll*i-1)%MOD;
    }
    return ans;
}

线性筛/欧拉筛

1
2
3
4
5
6
7
8
9
10
11
12
13
int primes[maxn / 10];// 质数 2，3，5，7...排列好的数组
bool isPrime[maxn + 5];//isPrime[i] :i是质数吗？
int tot=0;//质数的个数

void init(){
    for(int i = 2; i <= maxn; i++){
        if (!isPrime[i]) primes[tot++] = i;
        for(int j = 0; i * primes[j] <= maxn; j++){
            isPrime[i * primes[j]] = 1;
            if (i % primes[j] == 0) break;
        }
    }
}

STL

基础

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
vector, 变长数组，倍增的思想
    size()  返回元素个数
    empty()  返回是否为空
    clear()  清空
    front()/back()
    push_back()/pop_back()
    begin()/end()
    []
    支持比较运算，按字典序

pair<int, int>
    first, 第一个元素
    second, 第二个元素
    支持比较运算，以first为第一关键字，以second为第二关键字（字典序）

string，字符串
    size()/length()  返回字符串长度
    empty()
    clear()
    substr(起始下标，(子串长度))  返回子串
    c_str()  返回字符串所在字符数组的起始地址

queue, 队列
    size()
    empty()
    push()  向队尾插入一个元素
    front()  返回队头元素
    back()  返回队尾元素
    pop()  弹出队头元素

priority_queue, 优先队列，默认是大根堆
    size()
    empty()
    push()  插入一个元素
    top()  返回堆顶元素
    pop()  弹出堆顶元素
    定义成小根堆的方式：priority_queue<int, vector<int>, greater<int>> q;

stack, 栈
    size()
    empty()
    push()  向栈顶插入一个元素
    top()  返回栈顶元素
    pop()  弹出栈顶元素

deque, 双端队列
    size()
    empty()
    clear()
    front()/back()
    push_back()/pop_back()
    push_front()/pop_front()
    begin()/end()
    []

set, map, multiset, multimap, 基于平衡二叉树（红黑树），动态维护有序序列
    size()
    empty()
    clear()
    begin()/end()
    ++, -- 返回前驱和后继，时间复杂度 O(logn)

    set/multiset
        insert()  插入一个数
        find()  查找一个数
        count()  返回某一个数的个数
        erase()
            (1) 输入是一个数x，删除所有x   O(k + logn)
            (2) 输入一个迭代器，删除这个迭代器
        lower_bound()/upper_bound()
            lower_bound(x)  返回大于等于x的最小的数的迭代器
            upper_bound(x)  返回大于x的最小的数的迭代器
    map/multimap
        insert()  插入的数是一个pair
        erase()  输入的参数是pair或者迭代器
        find()
        []  注意multimap不支持此操作。 时间复杂度是 O(logn)
        lower_bound()/upper_bound()

unordered_set, unordered_map, unordered_multiset, unordered_multimap, 哈希表
    和上面类似，增删改查的时间复杂度是 O(1)
    不支持 lower_bound()/upper_bound()， 迭代器的++，--

bitset, 圧位
    bitset<10000> s;
    ~, &, |, ^
    >>, <<
    ==, !=
    []

    count()  返回有多少个1

    any()  判断是否至少有一个1
    none()  判断是否全为0

    set()  把所有位置成1
    set(k, v)  将第k位变成v
    reset()  把所有位变成0
    flip()  等价于~
    flip(k) 把第k位取反

lower_bound/upper_bound

设我们有一个数x，并保证a数组从小到大排好

upper_bound( a,a+n,x)：从数组的begin位置到end-1位置二分查找第一个大于x的数字，找到返回该数字的地址，不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。

lower_bound( a,a+n,x)：从数组的begin位置到end-1位置二分查找第一个大于或等于x的数字，找到返回该数字的地址，不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。

在数组a[5]={0,2,3,4,5}中，对于需要查找的x=2

lower_bound(a,a+n,x)-a 返回值为1，表示数组中第一个大于等于x的下标值

upper_bound(a,a+n,x)-a 返回值为2，表示数组中第一个大于x的下标值

上面是对于非递减数列的用法，那对于非递增数列的用法呢？
这时候我们就需要传入第四个参数 $greater()$ 其中TYPE是指数组类型
这时候我们lower_bound就是返回数组中第一个小于或等于x的数的位置，upper_bound就返回数组中第一个小于x的数的位置了。
找不到会返回a.end()/a[n+1]

unorder_map防止被卡O(n)写法

不同于map的红黑树实现，unorder_map的有hash实现，一般来说查找是O(1)的，而不是O(log)的，但是CF上有时会被hack成O(n)的，因此提出这种写法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
struct my_hash {
  static uint64_t splitmix64(uint64_t x) {
    x += 0x9e3779b97f4a7c15;
    x = (x ^ (x >> 30)) * 0xbf58476d1ce4e5b9;
    x = (x ^ (x >> 27)) * 0x94d049bb133111eb;
    return x ^ (x >> 31);
  }

  size_t operator()(uint64_t x) const {
    static const uint64_t FIXED_RANDOM =
        chrono::steady_clock::now().time_since_epoch().count();
    return splitmix64(x + FIXED_RANDOM);
  }

  // 针对 std::pair<int, int> 作为主键类型的哈希函数
  size_t operator()(pair<uint64_t, uint64_t> x) const {
    static const uint64_t FIXED_RANDOM =
        chrono::steady_clock::now().time_since_epoch().count();
    return splitmix64(x.first + FIXED_RANDOM) ^
           (splitmix64(x.second + FIXED_RANDOM) >> 1);
  }
};

写完自定义的哈希函数后，就可以通过 unordered_map<int, int, my_hash> my_map; 或者 unordered_map<pair<int, int>, int, my_hash> my_pair_map; 的定义方式将自定义的哈希函数传入容器了。

map自定义排列顺序：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
//记录大数据点
#include <bits/stdc++.h>
using namespace std;
struct Node{
    int x,y;
    Node() {}
    Node(int x,int y):x(x),y(y) {}
    bool operator < (const Node &rhs) const {
		return x < rhs.x;
	} 
};
map<Node,int>mp;
int main()
{
    int x1,y1;
    while(cin>>x1>>y1) {
        if(x1 == 0&& y1 == 0) break;
        Node temp = Node(x1,y1);
        if(!mp.count(temp)) {
            mp[temp] = 1;
        }
        else mp[temp]++;
    }
    for(auto &u:mp) {
        cout<<u.first.x<<" "<<u.first.y<<" "<<u.second<<endl;
    }
    return 0;
}

set自定义顺序

set是一种关联式容器，所以有顺序，下面给出自定义顺序写法。

1
2
3
4
struct cmp {
  bool operator()(int a, int b) { return a > b; }
};
set<int, cmp> s;

数据结构

ST表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
struct RMQ{
    ll f1[22][MAXN],f2[22][MAXN];
    inline int highbit(ll x) {return 31 - __builtin_clz(x);}
    void init(ll *v,int n) {
        for(int i = 0;i < n;i++) f1[0][i] = f2[0][i]= v[i];
        for(int x = 1;x <= highbit(n);x++)
            for(int i = 0;i <= n - (1 << x);i++) {
                f1[x][i] = min(f1[x - 1][i],f1[x - 1][i + (1 << (x - 1))]);
                f2[x][i] = max(f2[x - 1][i],f2[x - 1][i + (1 << (x - 1))]);
            }
    }
    ll get_min(int l,int r) {
        assert(l <= r);
        int t = highbit(r - l + 1);
        return min(f1[t][l],f1[t][r - (1 << t) + 1]);
    }
    ll get_max(int l,int r) {
        assert(l <= r);
        int t = highbit(r - l + 1);
        return max(f2[t][l],f2[t][r - (1 << t) + 1]);
    }
};

//use
int array[]....
RMQ st;
st.init(array,n); //

单调队列

复杂度O(n)

在长度为n的序列中求每个长度为m的区间最值

1
2
3
4
5
6
7
8
9
10
11
12
//求区间最大值
deque<int> Q; // 存储的是编号
for (int i = 0; i < n; ++i)
{
    if (!Q.empty() && i - Q.front() >= m) // 毕业
        Q.pop_front();
    while (!Q.empty() && V[Q.back()] < V[i]) // 比新生弱的当场退役（求区间最小值把这里改成>即可）
        Q.pop_back();
    Q.push_back(i); // 新生入队
    if (i >= m - 1)
        cout << V[Q.front()] << " ";
}

单调栈

求NGE(Next greater element)问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int n;
cin >> n;
vector<int> V(n + 1), ans(n + 1);
for (int i = 1; i <= n; ++i)
    cin >> V[i];
stack<int> S;
for (int i = 1; i <= n; ++i)
{
    while (!S.empty() && V[S.top()] < V[i])
    {
        ans[S.top()] = i;
        S.pop();
    }
    S.push(i);
}
for (int i = 1; i <= n; ++i)
    cout << ans[i] << " ";

线段树

单点修改+区间查询 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
struct Node{
    int l,r;
    int v;
}tr[4*MAXN];

void pushup(int u)
{
    tr[u].v = max(tr[u<<1].v,tr[u<<1|1].v);
}

void build(int u,int l,int r)
{
    tr[u] = {l,r};
    if(l==r) return;
    int mid = l + r >> 1;
    build(u<<1,l,mid);
    build(u<<1|1,mid+1,r);
}
//查询区间最大
int query(int u,int l,int r)
{
    if(tr[u].l>=l&&tr[u].r<=r) return tr[u].v;//树中节点已经被完全包含在[l,r]中
    int mid = tr[u].l + tr[u].r >> 1;
    int v = 0;
    if(l<=mid) v = query(u<<1,l,r);
    if(l>mid) v = max(v,query(u<<1|1,l,r));
    return v;
}

void modify(int u,int x,int v)
{
    if(tr[u].l==x&&tr[u].r==x) tr[u].v = v;
    else
    {
        int mid = tr[u].l + tr[u].r >> 1;
        if(x<=mid) modify(u<<1,x,v);
        else modify(u<<1|1,x,v);
        pushup(u);
    }
}

区间修改+区间查询：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
typedef long long ll;
const int INF=0x3f3f3f3f;
const int MAXN=5e5+2;
const int MOD=998244353;
const double pi=acos(-1);
const double eps=1e-4;

int w[MAXN];

struct Node{
    int l,r;
    ll sum,add;
}tr[4*MAXN];

void pushup(int u)
{
    tr[u].sum = tr[u<<1].sum + tr[u<<1|1].sum;
}

void pushdown(int u)
{
    auto &root = tr[u], &left = tr[u<<1], &right = tr[u<<1|1];
    if(root.add)
    {
        left.add += root.add,left.sum += (ll)(left.r - left.l  + 1)*root.add;
        right.add += root.add,right.sum += (ll)(right.r-right.l + 1)*root.add;
        root.add = 0;
    }
}

void build(int u,int l,int r)
{
    if(l==r) tr[u] = {l,r,w[r],0};
    else
    {
        tr[u] = {l,r};
        int mid = l+r>>1;
        build(u<<1,l,mid);
        build(u<<1|1,mid+1,r);
        pushup(u);
    }
}

//区间修改(区间加d)
void modify(int u,int l,int r,int d)
{
    if(tr[u].l>=l&&tr[u].r<=r)
    {
        tr[u].sum += (ll)(tr[u].r - tr[u].l + 1)*d;
        tr[u].add += d;
    }
    else
    {
        pushdown(u);
        int mid = tr[u].l + tr[u].r>>1;
        if(l<=mid) modify(u<<1,l,r,d);
        if(r>mid) modify(u<<1|1,l,r,d);
        pushup(u);
    }
}
//区间查询sum
ll query(int u,int l,int r)
{
    if(tr[u].l>=l&&tr[u].r<=r) return tr[u].sum;
    pushdown(u);
    int mid = tr[u].l + tr[u].r>>1;
    ll sum = 0;
    if(l<=mid) sum += query(u<<1,l,r);
    if(r>mid) sum += query(u<<1|1,l,r);
    return sum;
}

int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>w[i];
    build(1,1,n);
    char op[2];
    int l,r,d;
    while(m--)
    {
        cin>>op>>l>>r;
        if(*op=='C')
        {
            cin>>d;
            modify(1,l,r,d);
        }
        else cout<<query(1,l,r)<<endl;
    }
    return 0;
}

Trie树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
int son[N][26], cnt[N], idx;
// 0号点既是根节点，又是空节点
// son[][]存储树中每个节点的子节点
// cnt[]存储以每个节点结尾的单词数量

// 插入一个字符串
void insert(char *str)
{
    int p = 0;
    for (int i = 0; str[i]; i ++ )
    {
        int u = str[i] - 'a';
        if (!son[p][u]) son[p][u] = ++ idx;
        p = son[p][u];
    }
    cnt[p] ++ ;
}

// 查询字符串出现的次数
int query(char *str)
{
    int p = 0;
    for (int i = 0; str[i]; i ++ )
    {
        int u = str[i] - 'a';
        if (!son[p][u]) return 0;
        p = son[p][u];
    }
    return cnt[p];
}

并查集

朴素并查集：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
int p[N]; //存储每个点的祖宗节点

// 返回x的祖宗节点
int find(int x)
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

// 初始化，假定节点编号是1~n
for (int i = 1; i <= n; i ++ ) p[i] = i;

// 合并a和b所在的两个集合：
p[find(a)] = find(b);


//按秩合并
void unite(int x,int y)
{
    x=find(x);
    y=find(y);
    if(x==y) return ;
    if(rank[x]<rank[y])
        parent[x]=y;  // 合并是从rank小的向rank大的连边
    else
    {
        parent[y]=x;
        if(rank[x]==rank[y]) rank[x]++;
    }
}

//防止爆栈，非递归版本
int find(int x){
    int p=x;
    while(p!=fa[p])
        p=fa[p];
    while(x!=p){
        int tmp=fa[x];
        fa[x]=p;
        x=tmp;
    }
    return x;
}

维护size的并查集：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int p[N], size[N];
//p[]存储每个点的祖宗节点, size[]只有祖宗节点的有意义，表示祖宗节点所在集合中的点的数量

// 返回x的祖宗节点
int find(int x)
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

// 初始化，假定节点编号是1~n
for (int i = 1; i <= n; i ++ )
{
    p[i] = i;
    size[i] = 1;
}

// 合并a和b所在的两个集合：
size[find(b)] += size[find(a)];
p[find(a)] = find(b);

维护到祖宗节点距离的并查集：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
int p[N], d[N];
//p[]存储每个点的祖宗节点, d[x]存储x到p[x]的距离

// 返回x的祖宗节点
int find(int x)
{
    if (p[x] != x)
    {
        int u = find(p[x]);
        d[x] += d[p[x]];
        p[x] = u;
    }
    return p[x];
}

// 初始化，假定节点编号是1~n
for (int i = 1; i <= n; i ++ )
{
    p[i] = i;
    d[i] = 0;
}

// 合并a和b所在的两个集合：
p[find(a)] = find(b);
d[find(a)] = distance; // 根据具体问题，初始化find(a)的偏移量

树状数组

单点修改+区间查询：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
int n;
int tree[MAXN];
int a[MAXN];
int lowbit(int x) {return x&(-x);}
int getsum(int x)
{
    int ans_tep=0;
    for(int i=x;i>0;i-=lowbit(i)) ans_tep+=tree[i];
    return ans_tep;
}
void single_update(int x,int y)//第x个加y
{
    for(int i=x;i<=n;i+=lowbit(i)) tree[i]+=y;
}
int range_query(int x,int y)
{
    return getsum(y)-getsum(x-1);
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        single_add(i,a[i]);//单点更新来建立树
    }
    查询区间 range_query(int x,int y)
    查询前缀 getsum(int x)
    return 0;
}

区间修改+单点查询：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
int n;
int a[MAXN];
int tree_help[MAXN];//差分辅助树状数组
int lowbit(int x) {return x&(-x);}

void part_update(int x,int val)
{
    for(int i=x;i<=n;i+=lowbit(i)) tree_help[i]+=val;
}
void update_query(int l,int r,int val)
{
    part_update(l,val);
    part_update(r+1,-val);
}
int single_query(int x)
{
    int ans_tep=0;
    for(int i=x;i>0;i-=lowbit(i)) ans_tep+=tree_help[i];
    return ans_tep;
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        part_update(i,a[i]-a[i-1]);//单点更新建立tree_help[]
    }
    区间更新： update_query(int l,int r,int val);
    单点查询： single_query(int x);
    return 0;
}

区间修改+区间查询：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
//Chillstep ^_^
#include<bits/stdc++.h>
using namespace std;
#define pii pair<int,int>
#define pll pair<ll,ll>
#define pdd pair<double,double>
typedef long long ll;
const int INF=0x3f3f3f3f;
const int MAXN=5000+5;
const int MOD=1e9+7;
const double pi=cos(-1);

int n;
int a[MAXN];
int c1[MAXN],c2[MAXN];//差分辅助树状数组
int lowbit(int x) {return x&(-x);}
void update(int *o,int x,int val)
{
    for(int i=x;i<=n;i++)
    {
        o[x]+=val;
        x+=lowbit(x);
    }
}
int getsum(int *o,int x)
{
    int ans_tep=0;
    for(int i=x;i>0;i-=lowbit(x))
    {
        ans_tep+=o[x];
        x-=lowbit(x);
    }
    return ans_tep;
}
int sum(int x)
{
    int ans1_tep,ans2_tep;
    ans1_tep=x*getsum(c1,x);
    ans2_tep=getsum(c2,x);
    return ans1-ans2;
}
int range_quiry(int l,int r)
{
    int ans1_tep,ans2_tep;
    ans1=sum(r);
    ans2=sum(l-1);
    return ans1_tep-ans2_tep;
}
int update_range(int l,int r,int val)
{
    update(c1,l,val);
    update(c1,r+1,-val);
    update(c2,l,(l-1)*val);
    update(c2,r+1,-r*val);
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        update(c1,i,a[i]-a[i-1]);
        update(c2,i,(i-1)*(a[i]-a[i-1]));
    }
    区间更新： update_range(int l,int r,int val)
    区间查询： range_quiry(int l,int r);
    return 0;
}

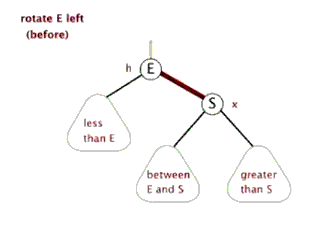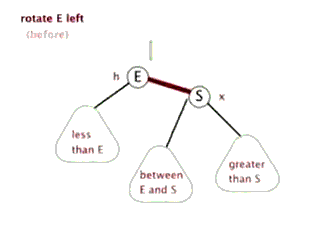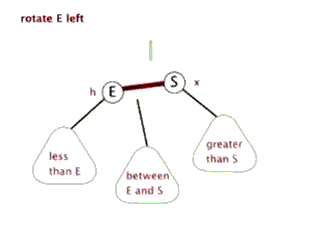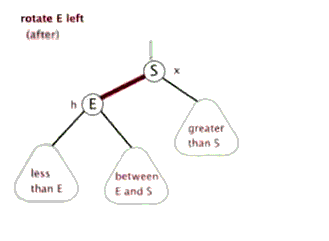
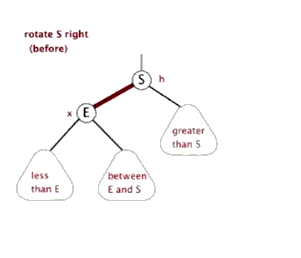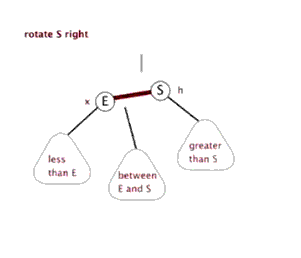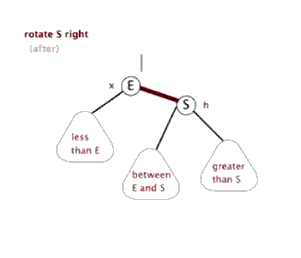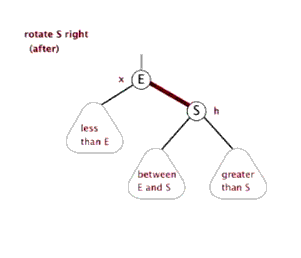
平衡树AVL

平衡树左旋

平衡树右旋

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
#include<bits/stdc++.h>
using namespace std;
#define pii pair<int,int>
#define pll pair<ll,ll>
#define pdd pair<double,double>
#define fastIO ios::sync_with_stdio(false);cin.tie(0);
#define fi first
#define se second
typedef long long ll;
const int INF=0x3f3f3f3f;
const int MAXN=5e5+2;
const int MOD=998244353;
const double pi=acos(-1);
const double eps=1e-4;

int n;

struct node
{
    int data;
    node *lchild,*rchild;
};
node *Newnode(int x)
{
    node* newnode = new node;
    newnode->data = x;
    newnode->lchild = newnode->rchild = nullptr;
    return newnode;
}
int height(node *root)
{
    if(root==nullptr) return 0;
    else return max(height(root->lchild),height(root->rchild)) + 1;
}
int getbalance(node* root)
{
    return height(root->lchild) - height(root->rchild);
}
void R(node*&root) //右旋
{
    node* temp = root->lchild;
    root->lchild = temp->rchild;//根的左节点->跟的右节点
    temp->rchild = root;
    root = temp;
}
void L(node*&root)//左旋
{
    node* temp = root->rchild;
    root->rchild = temp->lchild;
    temp->lchild = root;
    root = temp;
}

void inst(node* &root,int x)
{
    if(root==nullptr)
    {
        root = Newnode(x);
        return;
    }

    if(x<root->data)
    {
        inst(root->lchild,x);
        if(getbalance(root)==2)//左边比右边高
        {
            if(getbalance(root->lchild)==1) R(root);
            else if(getbalance(root->lchild)==-1) {L(root->lchild);R(root);}
        }
    }
    else
    {
        inst(root->rchild,x);
        if(getbalance(root)==-2)
        {
            if(getbalance(root->rchild)==1) {R(root->rchild);L(root);}
            else if(getbalance(root->rchild)==-1) L(root);
        }
    }

}

int main()
{

    cin>>n;
    node *root = nullptr;
    for(int i=0;i<n;i++)
    {
        int x;
        cin>>x;
        inst(root,x);
    }
    cout<<root->data<<endl;
    return 0;
}

图论

最短路

Dijkstra（单源最短路，正边权）：

无优化：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
int g[N][N];  // 存储每条边
int dist[N];  // 存储1号点到每个点的最短距离
bool st[N];   // 存储每个点的最短路是否已经确定

// 求1号点到n号点的最短路，如果不存在则返回-1
int dijkstra()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;

    for (int i = 0; i < n - 1; i ++ )
    {
        int t = -1;// 在还未确定最短路的点中，寻找距离最小的点
        for (int j = 1; j <= n; j ++ )
            if (!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;

        // 用t更新其他点的距离
        for (int j = 1; j <= n; j ++ )
            dist[j] = min(dist[j], dist[t] + g[t][j]);

        st[t] = true;
    }

    if (dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
//Chillstep ACM-Template
#include<bits/stdc++.h>
using namespace std;
#define pii pair<int,int>
#define pll pair<ll,ll>
#define pdd pair<double,double>
#define fastIO ios::sync_with_stdio(false);cin.tie(0);

typedef long long ll;
const int INF=0x3f3f3f3f;
const int MAXN=5e5+2;
const int MOD=998244353;
const double pi=acos(-1);
const double eps=1e-4;

int n,m;
int dist[MAXN];
bool st[MAXN];
vector<int>g[MAXN];
map<pii,int>w;
void dij(int src)
{
    memset(dist,0x3f,sizeof dist);
    dist[src]=0;
    priority_queue<pii,vector<pii>,greater<pii>>heap;
    heap.push({0,src});

    while(!heap.empty())
    {
        auto t = heap.top();
        heap.pop();

        int u = t.second,distance = t.first;
        if(st[u]) continue;
        else st[u] = true;

        for(int i=0;i<g[u].size();i++)
        {
            int v = g[u][i];
            if(dist[v]>distance+w[{u,v}])
            {
                dist[v] = distance + w[{u,v}];
                heap.push({dist[v],v});
            }
        }
    }
}


int main()
{
    cin>>n>>m;
    for(int i=1;i<=m;i++)
    {
        int x,y,z;
        cin>>x>>y>>z;
        g[x].push_back(y);
        w[{x,y}]=z;
    }
    dij(1);
    if(dist[n]==0x3f3f3f3f) cout<<-1<<endl;
    else cout<<dist[n]<<endl;
    return 0;
}

/*

*/

SPFA（单源最短路，正负边权皆可）:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#define N 100005
struct edge
{
    int v,w,nxt;
} e[N*2];
void add(int u,int v,int w)
{
    tot++;
    e[tot].v=v;
    e[tot].w=w;
    e[tot].nxt=head[u];
    head[u]=tot;
}
ll dis[M];
queue<int> Q;
bool vis[M];
void SPFA(int s)
{
    memset(dis,0x3F,sizeof(dis));
    dis[s] = 0;
    Q.push(s);
    vis[s]=1;
    while(!Q.empty())
    {
        int u=Q.front();
        Q.pop();
        vis[u]=0;
        for(int i=head[u]; i; i=e[i].nxt)
            if(dis[u]+e[i].w<dis[e[i].v])
            {
                dis[e[i].v]=dis[u]+e[i].w;
                if(!vis[e[i].v])
                {
                    vis[e[i].v]=1;
                    Q.push(e[i].v);
                }
            }
    }
}

Floyd $O(n^3)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
初始化：
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= n; j ++ )
            if (i == j) d[i][j] = 0;
            else d[i][j] = INF;

// 算法结束后，d[a][b]表示a到b的最短距离
void floyd()
{
    for (int k = 1; k <= n; k 
        for (int i = 1; i <= n; i ++ )
            for (int j = 1; j <= n; j ++ )
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}

DP

排序

手写堆

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
//Chillstep ACM-Template
#include<bits/stdc++.h>
using namespace std;
#define pii pair<int,int>
#define pll pair<ll,ll>
#define pdd pair<double,double>
#define fastIO ios::sync_with_stdio(false);cin.tie(0);

typedef long long ll;
const int INF=0x3f3f3f3f;
const int MAXN=5e5+2;
const int MOD=998244353;
const double pi=acos(-1);
const double eps=1e-4;

int a[11] = {0,10,5,13,14,1,23,44,1,22,23};
void adjust(int n,int i)
{
    int largest = i;
    if(i*2<=n&&a[largest]<a[i*2]) largest = i*2;
    if(i*2+1<=n&&a[largest]<a[i*2+1]) largest = i*2+1;
    if(largest!=i)
    {
        swap(a[largest],a[i]);
        adjust(n,largest);
    }
}


int main()
{
    int n = 10;
    //create max heap
    for(int i=n/2;i>=1;i--)
    {
        adjust(n,i);
    }
    //sort
    for(int i=n;i>=1;i--)
    {
        swap(a[1],a[i]);
        adjust(i-1,1);
    }
    for(int i=1;i<=n;i++) cout<<a[i]<<" ";
    cout<<endl;
    return 0;
}

奇怪的知识

  • 对于小于n的所有素数$p$，$\sum 1/p=loglogn$
  • 对于小于n的所有正整数$x$，$\sum 1/x = logn$，也就是调和级数

无极鲅鱼

  • 请检查是否应该开long long
  • 每个test case清空数组的时候应当大一些，比如清空1到n的时候，请尝试清楚1到n+1，因为上一个test case的n+1可能会影响到这一次的结果。
  • #pragma comment(linker, "/STACK:10240000000000,10240000000000") 手动开栈
  • 再读一边题目，是否读错了题目。
  • 自定义比较函数别用<= 最好定义<
  • endl太慢，用"\n" 或者 #define endl "\n"