(A-G)NEC Programming Contest 2021(AtCoder Beginner Contest 229)

(A-G)NEC Programming Contest 2021(AtCoder Beginner

A - First Grid

当且仅当有两个#需要判断，其他直接输出YES。当有两个#时，判断这两个#是否在对角线即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include<bits/stdc++.h>
using namespace std;
#define pii pair<int,int>
#define pll pair<ll,ll>
#define pdd pair<double,double>
#define fastIO ios::sync_with_stdio(false);cin.tie(0);

typedef long long ll;
const int INF=0x3f3f3f3f;
const int MAXN=2e5+7;
const long long MOD=1e9+7;
const double pi=acos(-1);
const double eps=1e-4;


int main()
{
    fastIO
    string s[2];
    cin>>s[0];
    cin>>s[1];
    int cnt = 0;
    for(auto ch:s[0])
    {
        if(ch=='#') cnt++;
    }
    for(auto ch:s[1])
    {
        if(ch=='#') cnt++;
    }
    if(cnt==2)
    {
        if(s[0][0]==s[1][1]) cout<<"No"<<endl;
        else cout<<"Yes"<<endl;
    }
    else cout<<"Yes"<<endl;


    return 0;
}

B - Hard Calculation

模拟题，模拟意义下大数加法，判断是否进位即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include<bits/stdc++.h>
using namespace std;
#define pii pair<int,int>
#define pll pair<ll,ll>
#define pdd pair<double,double>
#define fastIO ios::sync_with_stdio(false);cin.tie(0);

typedef long long ll;
const int INF=0x3f3f3f3f;
const int MAXN=2e5+7;
const long long MOD=1e9+7;
const double pi=acos(-1);
const double eps=1e-4;


int main()
{
    fastIO
    string s1,s2;
    cin>>s1>>s2;
    reverse(s1.begin(),s1.end());
    reverse(s2.begin(),s2.end());
    bool hard = false;
    for(int i=0;i<min(s1.size(),s2.size());i++)
    {
        int x = s1[i] - '0';
        int y = s2[i] - '0';
        if(x+y>=10) hard = true;
        if(hard) {break;}
    }
    if(hard) cout<<"Hard"<<endl;
    else cout<<"Easy"<<endl;


    return 0;
}

C - Cheese

贪心题，按照a排序，贪心的从前往后拿即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include<bits/stdc++.h>
using namespace std;
#define pii pair<int,int>
#define pll pair<ll,ll>
#define pdd pair<double,double>
#define fastIO ios::sync_with_stdio(false);cin.tie(0);

typedef long long ll;
const int INF=0x3f3f3f3f;
const int MAXN=3e5+7;
const long long MOD=1e9+7;
const double pi=acos(-1);
const double eps=1e-4;

pii a[MAXN];
int main()
{
    fastIO

    int n,w;
    cin>>n>>w;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i].first>>a[i].second;
    }
    sort(a+1,a+1+n,greater<pii>());
    ll ans = 0;
    for(auto [d,cnt]:a)
    {
        if(cnt<=w)
        {
            w -= cnt;
            ans += 1ll*cnt*d;
        }
        else
        {
            //w = 0;
            ans += 1ll*w*d;
            w = 0;
        }
        if(w==0) break;
    }
    cout<<ans<<endl;


    return 0;
}

D - Longest X

二分，考虑预处理前缀$pre[]$表示前i个字符有多少个$.$ ，然后对于每个前缀$pre[i]$，在数组$pre[]$中二分第一个大于$pre[i-1]+k$的位置$idx$,然后让$idx—$,也就是最后一个小于等于$pre[i-1]+k$的位置，那么$idx-pre[i]+1$就是从第$i$个字符开始可以做到的最长连续序列的长度。其他位置同理照做，复杂度$O(nlogn)$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include<bits/stdc++.h>
using namespace std;
#define pii pair<int,int>
#define pll pair<ll,ll>
#define pdd pair<double,double>
#define fastIO ios::sync_with_stdio(false);cin.tie(0);

typedef long long ll;
const int INF=0x3f3f3f3f;
const int MAXN=3e5+7;
const long long MOD=1e9+7;
const double pi=acos(-1);
const double eps=1e-4;

int pre[MAXN];
int main()
{
    fastIO

    string s;
    cin>>s;
    int n = s.size();
    s = "v" + s;
    int k;
    cin>>k;
    for(int i=1;i<=n;i++)
    {

        pre[i] = pre[i-1] + (s[i]=='.');
    }
    int ans = 0;
    for(int i=1;i<=n;i++)
    {
        int idx = upper_bound(pre+i,pre+1+n,k+pre[i-1]) - pre;
        if(idx!=n+1)
        {
            idx--;
            ans = max(ans,idx - i + 1);
        }
        else ans = max(n - i + 1,ans);
    }
    cout<<ans<<endl;
    return 0;
}

E - Graph Destruction

并查集，倒着建立并查集即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include<bits/stdc++.h>
using namespace std;
#define pii pair<int,int>
#define pll pair<ll,ll>
#define pdd pair<double,double>
#define fastIO ios::sync_with_stdio(false);cin.tie(0);

typedef long long ll;
const int INF=0x3f3f3f3f;
const int MAXN=3e5+7;
const long long MOD=1e9+7;
const double pi=acos(-1);
const double eps=1e-4;



vector<int>g[MAXN];
int p[MAXN]; //存储每个点的祖宗节点

// 返回x的祖宗节点
int find(int x)
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

// 初始化，假定节点编号是1~n


// 合并a和b所在的两个集合：
void un(int a,int b) {p[find(a)] = find(b);}

int main()
{
    fastIO
    int n,m;
    cin>>n>>m;
    for (int i = 1; i <= n; i ++ ) p[i] = i;
    for(int i=1;i<=m;i++)
    {
        int x,y;
        cin>>x>>y;
        g[x].push_back(y);
        g[y].push_back(x);
    }
    vector<int>ans;
    int cnt = 0;

    for(int i=n;i>=1;i--)
    {
        cnt++;
        for(auto v:g[i])
        {
            if(v>i&&find(i)!=find(v)) {un(i,v);cnt--;}
        }
       // cout<<cnt<<endl;
        ans.push_back(cnt);
    }
    for(int i=n-2;i>=0;i--) cout<<ans[i]<<" ";
    cout<<"0"<<endl;
    return 0;
}

F - Make Bipartite

DP题，希望我们去掉边后是一个二分图，我们可以采用染色的方法来表示二分图，即相邻的两个点颜色总是不同。

可以把中心点$0$设为黑色(用1表示)，设为白色(用$0$表示)同理等价。

设状态$dp[i][j][sorce]$表示染色到第$i$个点，将第$i$个点染色为$j$颜色，且顶点$1$的颜色为$sorce$已经删去的边权

然后从点$1$开始染色，顶点1可以是白色/黑色，因此初始状态有两种:$dp[1][0][0]=0,dp[1][1][1] = a[i]$ ,$dp[1][1][1]$由于顶点0也是黑色，如果顶点1也想染成黑色，那么就必须切断$a[1]$这条边。

转移就是四种：

1
2
3
4
dp[i][0][1] = min(dp[i-1][0][1]+b[i-1],dp[i-1][1][1]);
dp[i][1][1] = min(dp[i-1][0][1]+a[i],dp[i-1][1][1]+a[i]+b[i-1]);
dp[i][1][0] = min(dp[i-1][0][0]+a[i],dp[i-1][1][0]+a[i]+b[i-1]);
dp[i][0][0] = min(dp[i-1][0][0]+b[i-1],dp[i-1][1][0]);

最后计算答案时我们要比较四个：

即$dp[n][1][1]+b[n]$,$dp[n][0][0]+b[n]$(因为顶点1和顶点n颜色一样，那么要断掉外边$b[n]$) 和 $dp[n][1][0],dp[n][0][1]$

1
min({dp[n][1][1]+b[n],dp[n][0][0]+b[n],dp[n][1][0],dp[n][0][1]})
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include<bits/stdc++.h>
using namespace std;
#define pii pair<int,int>
#define pll pair<ll,ll>
#define pdd pair<double,double>
#define fastIO ios::sync_with_stdio(false);cin.tie(0);
#define endl "\n"
typedef long long ll;
const int INF=0x3f3f3f3f;
const int MAXN=5e5+7;
const long long MOD=998244353;
const double pi=acos(-1);
const double eps=1e-4;
vector<int>di = {-1, 1, 0, 0}, dj = {0, 0, -1, 1};

//unsigned seed = std::chrono::system_clock::now().time_since_epoch().count();
//mt19937 rand_num(seed);

ll dp[MAXN][2][2];
ll a[MAXN],b[MAXN];
int main()
{
    fastIO

    memset(dp,INF,sizeof dp);
    //v0 is black(1)
    int n;
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=1;i<=n;i++) cin>>b[i];
    dp[1][1][1] = a[1];
    dp[1][0][0] = 0;
    for(int i=2;i<=n;i++)
    {
        dp[i][0][1] = min(dp[i-1][0][1]+b[i-1],dp[i-1][1][1]);
        dp[i][1][1] = min(dp[i-1][0][1]+a[i],dp[i-1][1][1]+a[i]+b[i-1]);
        dp[i][1][0] = min(dp[i-1][0][0]+a[i],dp[i-1][1][0]+a[i]+b[i-1]);
        dp[i][0][0] = min(dp[i-1][0][0]+b[i-1],dp[i-1][1][0]);
    }
    cout<<min({dp[n][1][1]+b[n],dp[n][0][0]+b[n],dp[n][1][0],dp[n][0][1]})<<endl;



    return 0;
}

G - Longest Y

这题要有一些前置的知识：

首先考虑在一条数轴上，有n个工厂，现在希望在数轴上的找某一点，使得其他工厂到这个点的距离最小，这是最经典的贪心题，也就是绝对值不等式的应用，直接选择n个工厂位置的中位数即可。

现在回到我们这个题上，我们不放考虑二分答案$len$, 对于$check(len)$, 我们可以$O(n)$的枚举每个点最为$len$的中点(运用了上面的贪心性质)，然后利用一些维护技巧来$O(1)$的看看左边凑连续$len/2$个$Y$，右边凑连续$len - len/2$个$Y$的花费是否小于$K$。那么这个题就可做到$O(nlogn)$了。

那么剩下的问题就是如何$O(1)$维护左右连续某个数量的$Y$的花费是多少：

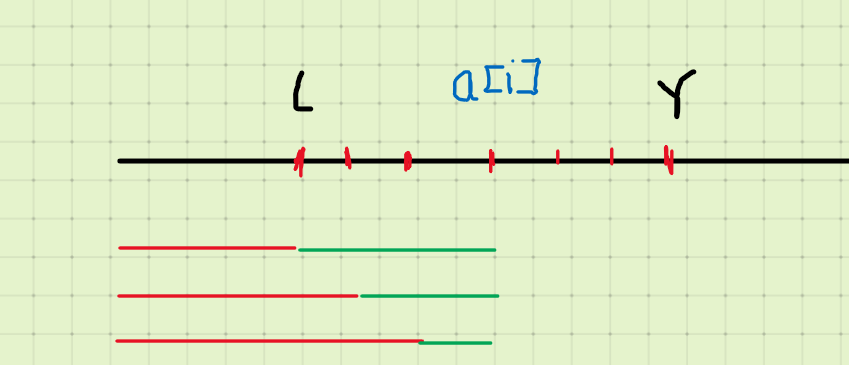
image-20211207154620742

对上面图，我们可以维护每个红色点的前缀和，我们可以O(1)查出三根红线长度和$red$，那么利用$3*a[i]-red$就是绿色线段的和，但是我们知道我们不是都移动到a[i],因为如果a[i]前面已经有Y了，那就只能移到这个Y的前面。因此我们其实是多计算了，$1+2+3$的距离。此时我们再减去这段多算的距离，就是左半部全部靠向$a[i]$的花费，此时我们就可以$O(1)$的维护了查询花费了。

右半部同理，但是细节很多，有点麻烦难写。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
#include<bits/stdc++.h>
using namespace std;
#define pii pair<int,int>
#define pll pair<ll,ll>
#define pdd pair<double,double>
#define fastIO ios::sync_with_stdio(false);cin.tie(0);
#define endl "\n"
typedef long long ll;
const int INF=0x3f3f3f3f;
const int MAXN=5e5+7;
const long long MOD=998244353;
const double pi=acos(-1);
const double eps=1e-4;
vector<int>di = {-1, 1, 0, 0}, dj = {0, 0, -1, 1};

//unsigned seed = std::chrono::system_clock::now().time_since_epoch().count();
//mt19937 rand_num(seed);

char s[MAXN];
ll k;
ll n,m;
ll a[MAXN];
ll pre[MAXN];
int ans = 0;

bool check(ll len)
{
   // cout<<"ch"<<len<<endl;
    ll lcnt = len/2+1;
    ll rcnt = len- lcnt;
    if(len>m) return false;
    ll minn = 1e18;
    for(int i=lcnt;i+rcnt<=m;i++)
    {
        //cout<<"beg:"<<i<<endl;
        ll tep = 1ll*lcnt*a[i] - 1ll*(pre[i] - pre[i-lcnt]) - 1ll*(1+lcnt-1)*(lcnt-1)/2;
        //cout<<lcnt*a[i]<<" "<<pre[i] - pre[i-lcnt]<<" "<<(1+lcnt-1)*(lcnt-1)/2<<endl;
        ll tep2= 1ll*(pre[i+rcnt] - pre[i]) - 1ll*rcnt*a[i] - 1ll*(1+rcnt)*rcnt/2;
       // cout<<(pre[i+rcnt] - pre[i])<<" "<<rcnt*a[i]<<" "<<(1+rcnt-1)*rcnt/2<<endl;
       // cout<<i<<" "<<tep<<" "<<tep2<<endl;
        tep = tep + tep2;
        minn=min(minn,tep);
    }
    //cout<<"ch: "<<len<<" "<<minn<<endl;
    if(minn<=k) return true;
    else return false;
}


int main()
{
    fastIO

    string ss;
    cin>>ss;

    n = ss.size();
    for(int i=0;i<ss.size();i++) s[i+1] = ss[i];
    cin>>k;
    for(int i=1;i<=n;i++)
    {
        if(s[i]=='Y') a[++m] = i;
    }
    for(int i=1;i<=m;i++) pre[i] = pre[i-1] + a[i];

    if(m==0) {cout<<0<<endl;return 0;}
    if(m==1) {cout<<1<<endl;return 0;}

    ll l = 2,r = n;
    while(l<r)
    {
        ll mid = l + r + 1 >> 1;
        if(check(mid)) l = mid;
        else r = mid - 1;
    }
    if(check(1ll*2)==false) cout<<1<<endl;
    else cout<<l<<endl;
    return 0;
}

END

ACM-Atcoder

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议 ，转载请注明出处！