RB-tree红黑树

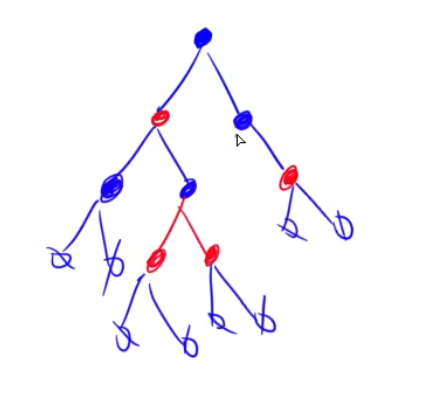
一些基本性质：

1.根节点一定是黑色

2.所有叶子结点(叶子结点都是空节点)都是黑色

3.红色结点的两个子结点一定是黑色

4.从任一个节点，到它每个叶子结点的路径都包含相同数目的黑色节点。

红黑树插入：

分三大类情况

1.被插入的节点是根节点，直接把此节点涂黑

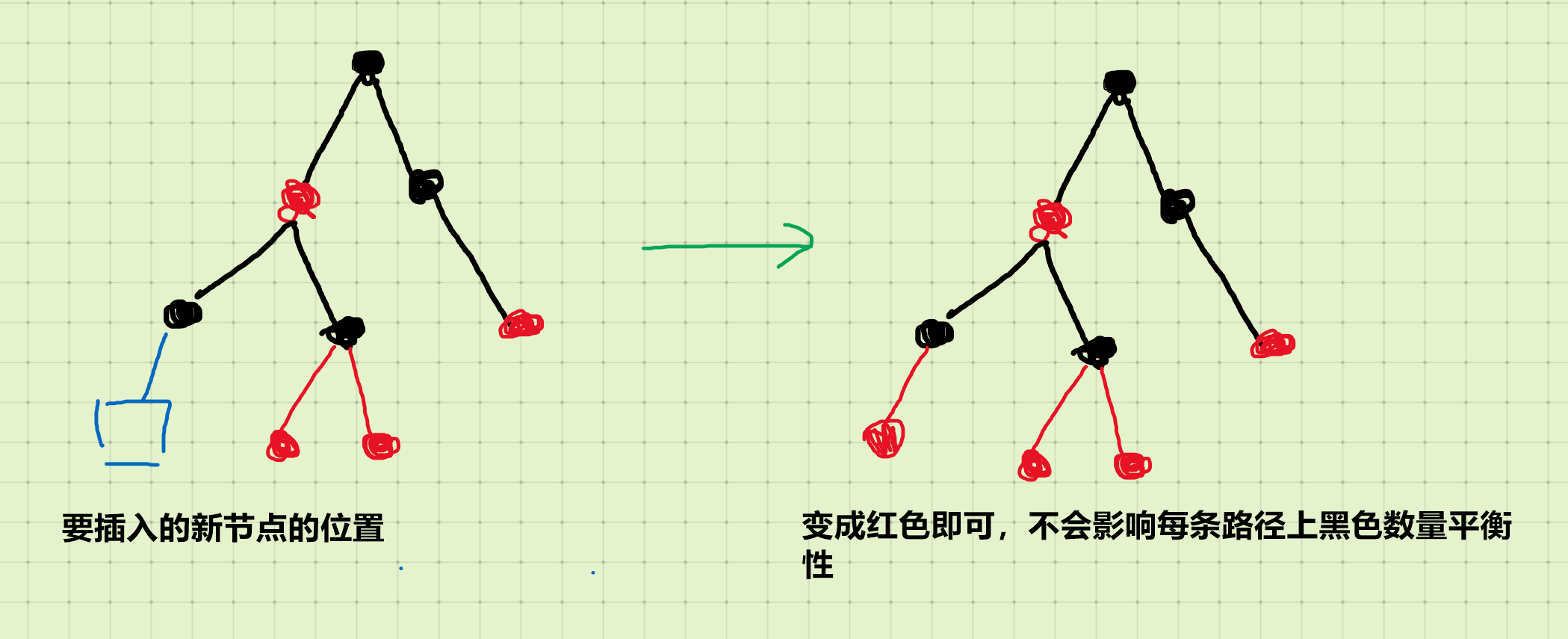
2.被插入的节点的父节点是黑色，直接插进去并且把节点变成红色(这是因为变成红色就不会影响上述的 基本性质4)

3.被插入的节点的父节点是红色，(由于红色只能挨着黑色，所以不能简单的插入后变红。)

• 3.1 叔叔节点也是红色(叔叔节点就是父节点的父节点的另一个儿子节点)

  ​ 父节点设为黑色，叔叔节点设为黑色，祖父节点设为红色，将祖父节点设为当前节点，之后对当前节点进行操作。

  

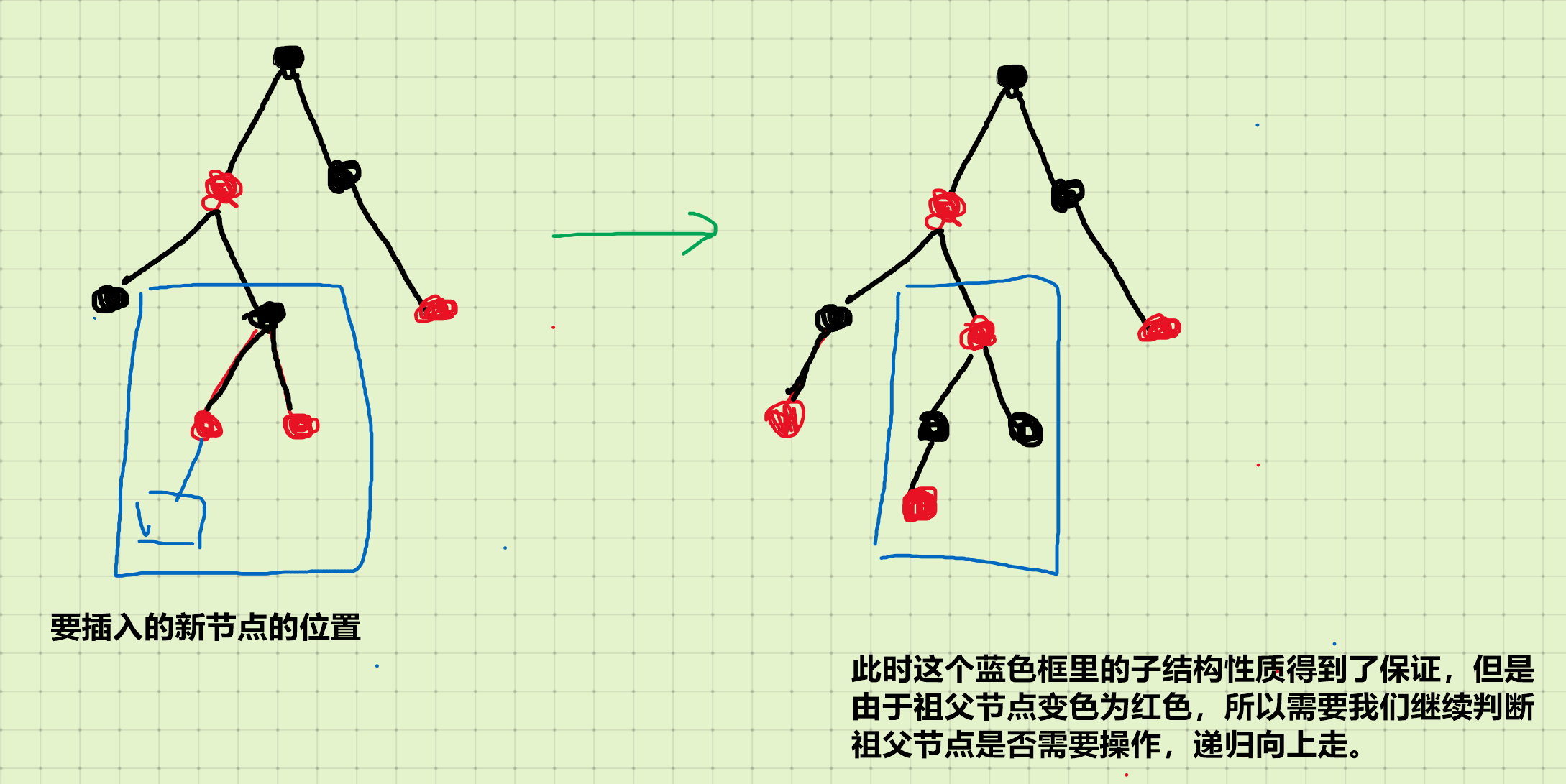
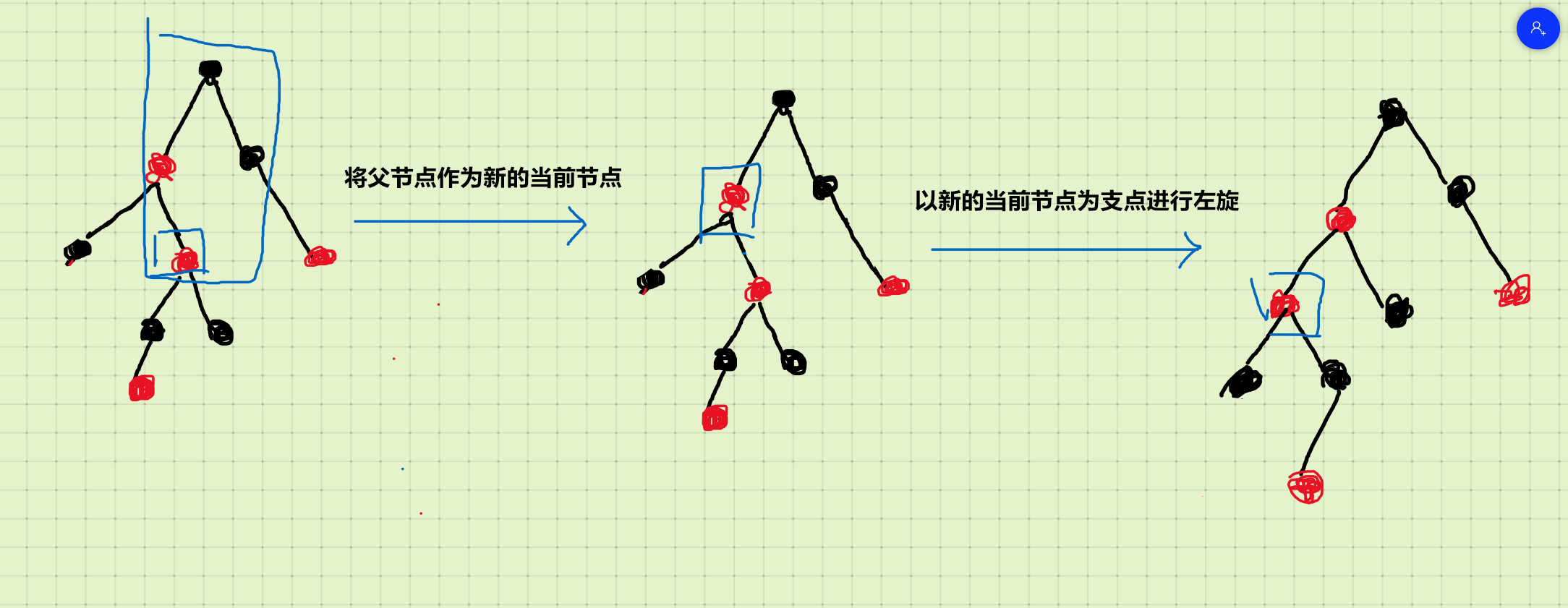
• 3.2 叔叔节点也是黑色，且当前点是父节点的右孩子

  ​ 将父节点作为新的当前节点，以新的当前节点为支点进行左旋：

  操作完后就会转化到3.3的情况

  

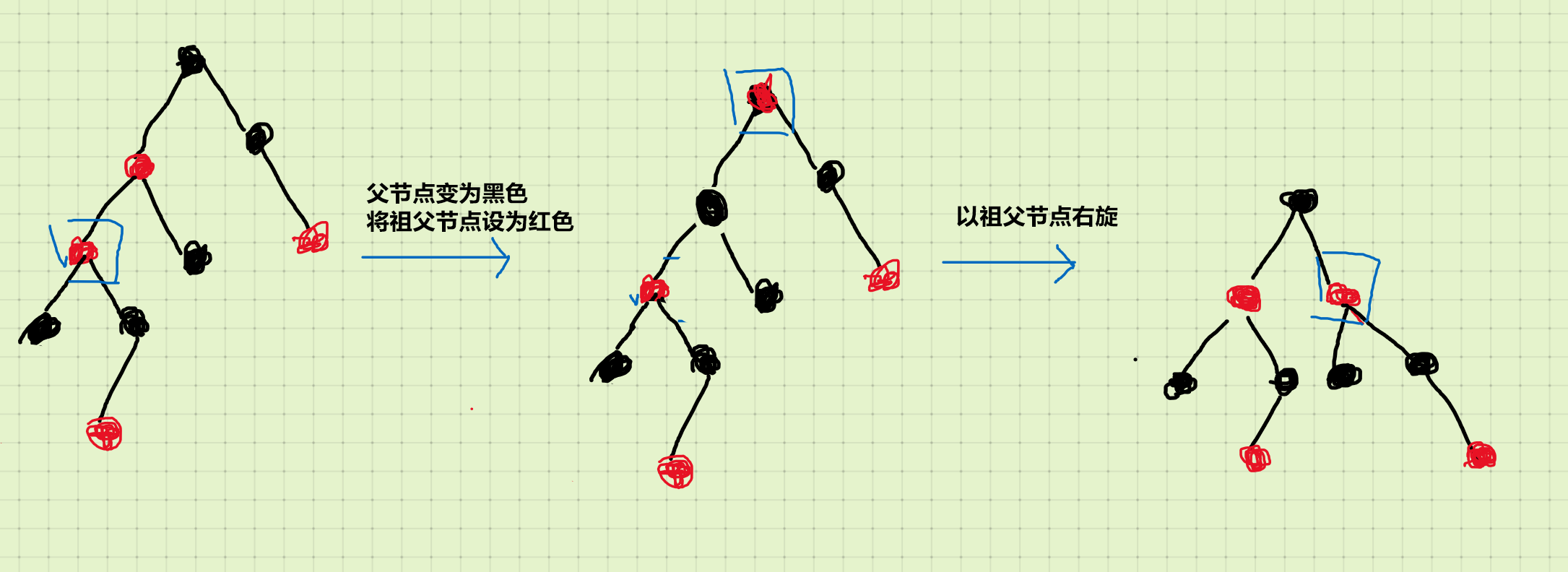
• 3.3 叔叔节点也是黑色，且当前点是父节点的左孩子

​ 将父节点变为黑色，将祖父节点设为红色，然后以祖父节点为支点右旋。

红黑树删除：

这里我们先解释一下在AVL中是如何删除的：

1.假如要删除的节点只有1个儿子，那么直接把儿子提上来即可。

2.假如要删除的节点有2个儿子，那么把右儿子的最左边节点提上来即可：

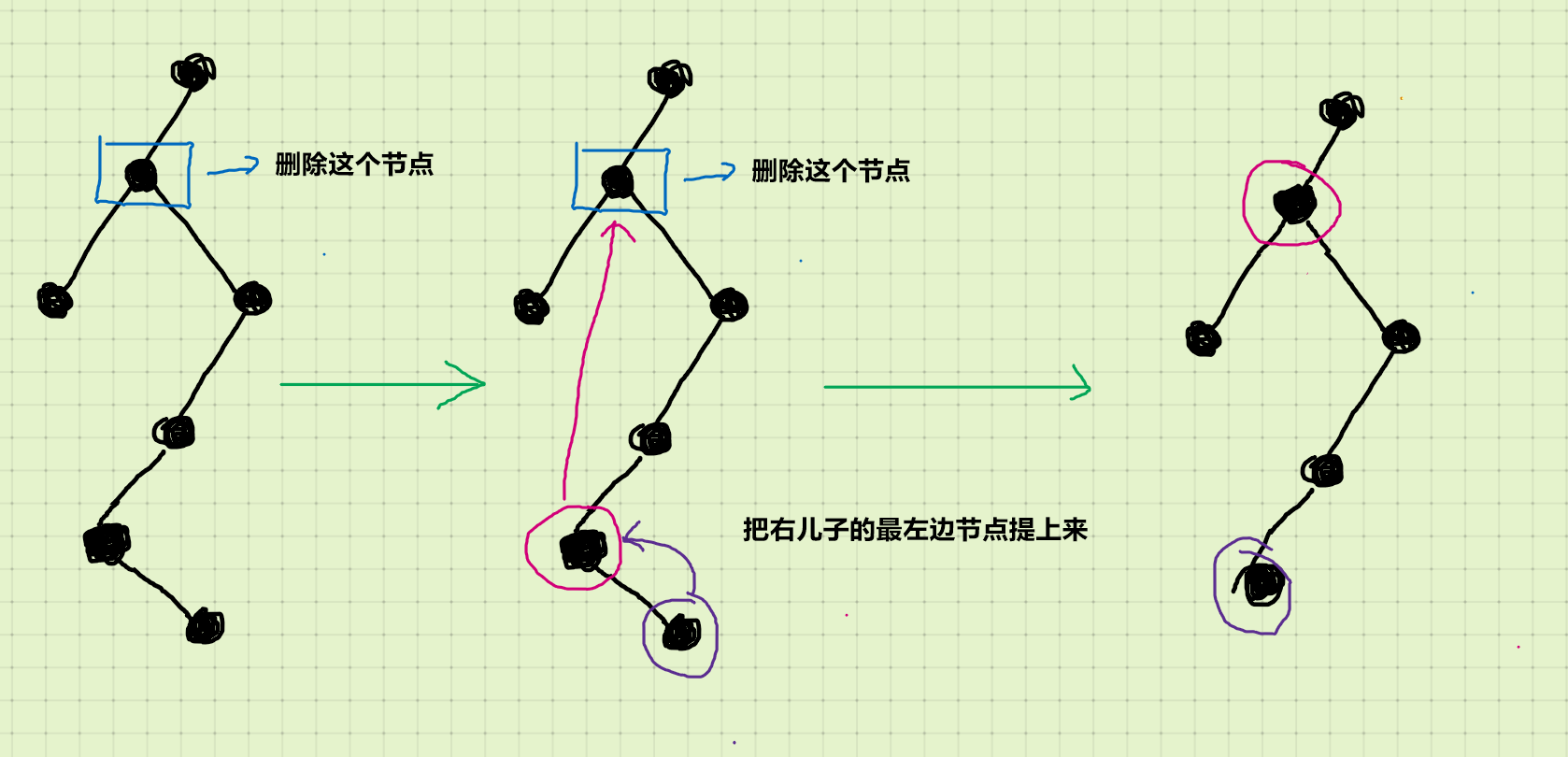
红黑树中删除和AVL的区别是还需要维护黑色平衡的性质：

1.如果删除的是红色点，那么我们什么也不需要做，因为这不会影响黑色平衡的性质，和AVL一样重新调整平衡即可。

2.如果删除的是黑色点：先提上来的结点颜色变为混合色：黑(要删除节点的颜色)+黑/红(提上来结点颜色) 的混合颜色。

• 2.1 黑+提上来的红色 ：结点设为黑色即可（因为提上来是的红色没了也不影响黑色平衡性，原来的黑色结点被删除后补上新的黑色保持了黑色平衡性）

• 2.2 根节点的黑(根节点一定为黑色)+提上来的黑色：结点设为黑色即可（因为从根节点开始，只是相当于从根节点开始的所有路径到叶子结点的黑色结点数全部减一，但不影响黑色平衡性）。

• 2.3 普通的黑色节点+提上来的黑色：

  设x为当前要删除的黑色节点。

  

红黑树和AVL比较：

1. 红黑树不追求”完全平衡”，即不像AVL那样要求节点的 |balFact| <= 1，它只要求部分达到平衡，但是提出了为节点增加颜色，红黑是用非严格的平衡来换取增删节点时候旋转次数的降低，任何不平衡都会在三次旋转之内解决，而AVL是严格平衡树，因此在增加或者删除节点的时候，根据不同情况，旋转的次数比红黑树要多。
2. 插入节点导致树失衡的情况，AVL和RB-Tree都是最多两次树旋转来实现复衡rebalance，旋转的量级是O(1)。
3. 删除节点导致失衡，AVL需要维护从被删除节点到根节点root这条路径上所有节点的平衡，旋转的量级为O(logN)，而RB-Tree最多只需要旋转3次实现复衡(注意:但是恢复红黑树的颜色性质需要少量logn的操作)，只需O(1)，所以说RB-Tree删除节点的rebalance的效率更高！
4. AVL的结构相较于RB-Tree更为平衡，插入和删除引起失衡，如2所述，RB-Tree复衡效率更高；当然，由于AVL高度平衡，因此AVL的Search效率更高。
5. 针对插入和删除节点导致失衡后的rebalance操作，红黑树能够提供一个比较”简单”的解决方案，降低开销，是对search，insert ，以及delete效率的折衷，总体来说，RB-Tree的统计性能高于AVL.

总结：引入RB-Tree是功能、性能、空间开销的折中结果。

1. AVL更平衡，结构上更加直观，search快一些；维护稍慢(因为AVL需要维护从被删除节点到根节点root这条路径上所有节点的平衡，旋转的量级为O(logN) )，空间开销较大(每个节点需要额外两比特来表示左斜、平衡、右斜三种状态,红黑树的每个节点只需要额外一比特来表示红、黑两种颜色)。
2. 实际应用上，红黑树有着良好的稳定性和完整的功能，性能表现也很不错，综合实力强，在诸如STL的场景中需要稳定表现。

Reference：

关于AVL树和红黑树的一点看法

视频-红黑树