GAMES101-现代计算机图形学入门

Lec1: Overview

本课包含的几个基本的tipic：

• 光栅化 Rasterization

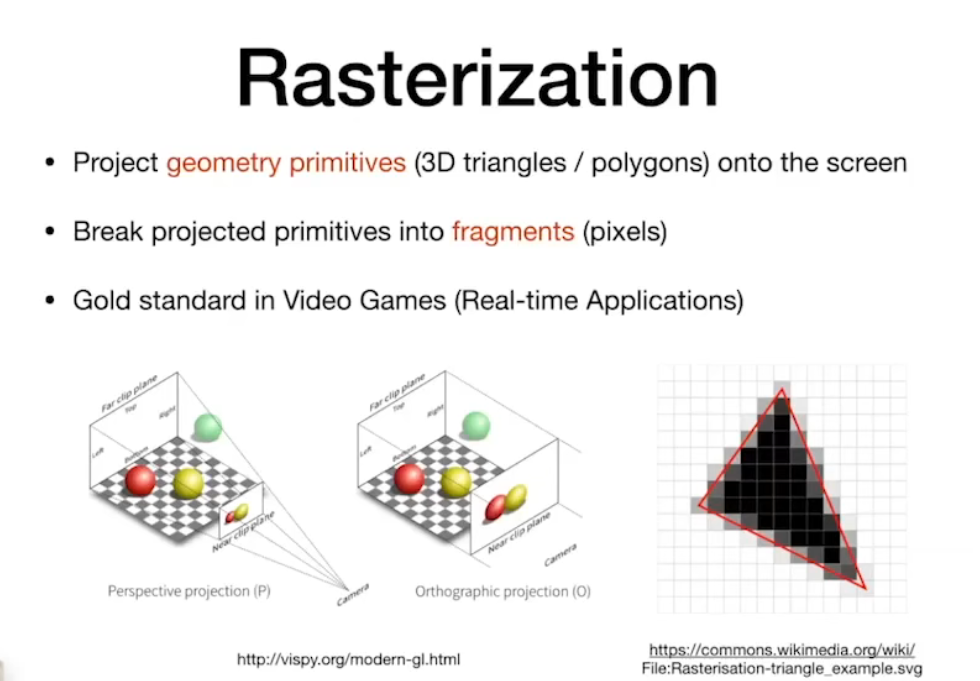
• 曲线/曲面Curves and Meshes

  

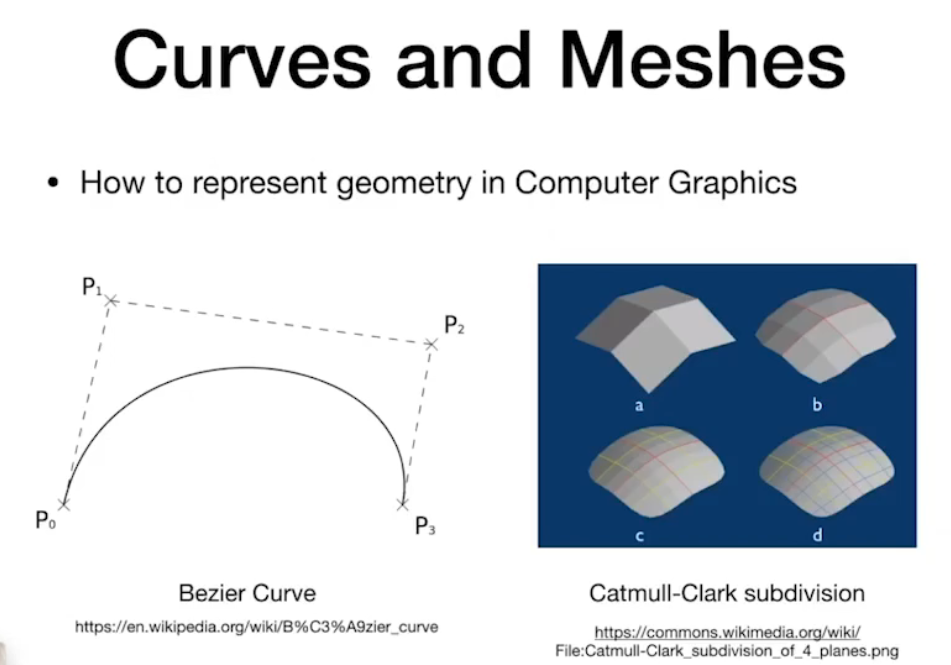
• 光线追踪 Ray Tracing

  

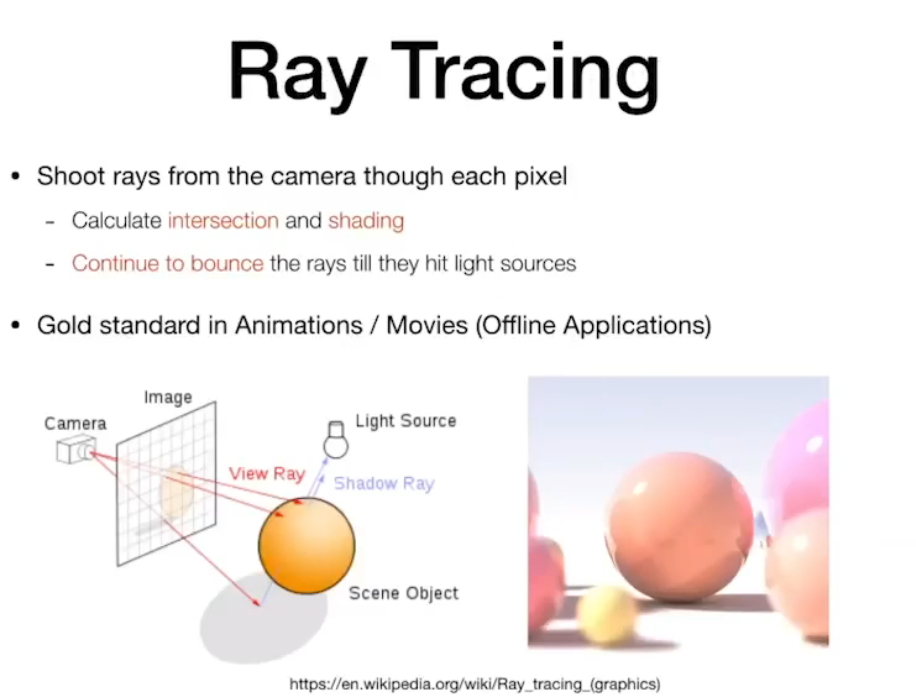
• 动画/模拟 Animation/Simulation

  

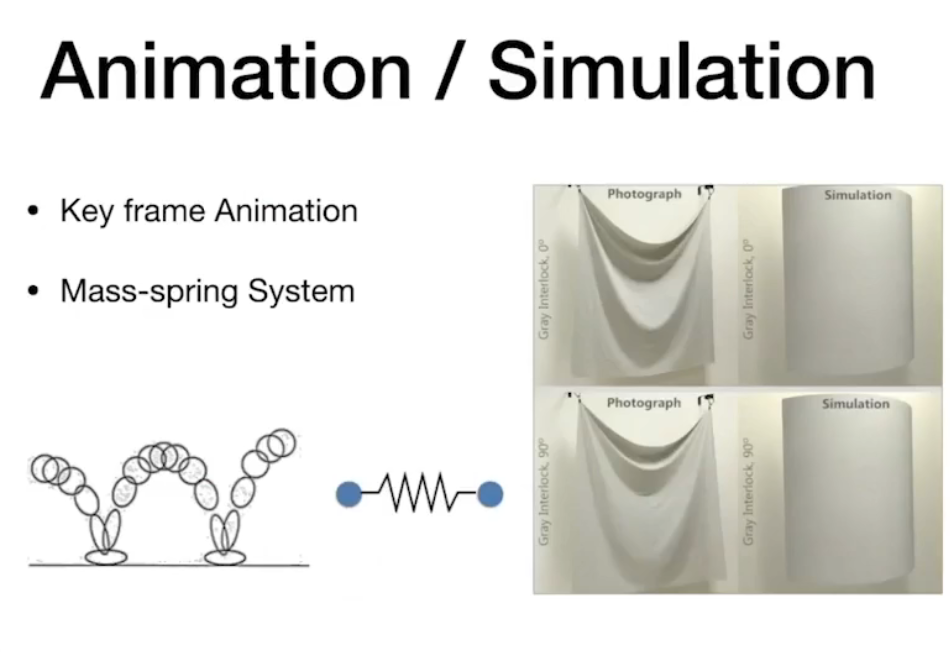
Lec2: Review of Linear Algebra

向量

• $\vec{a}$，代表一个方向，因此向量平移后还代表原向量。
• 单位向量：

$$\begin{align} \hat{a} & = \vec{a} /\|\vec{a}\| \end{align}$$

• 向量求和：平行四边形法则/三角形法则

点乘

• 点乘：常用于计算夹角/向量投影

  

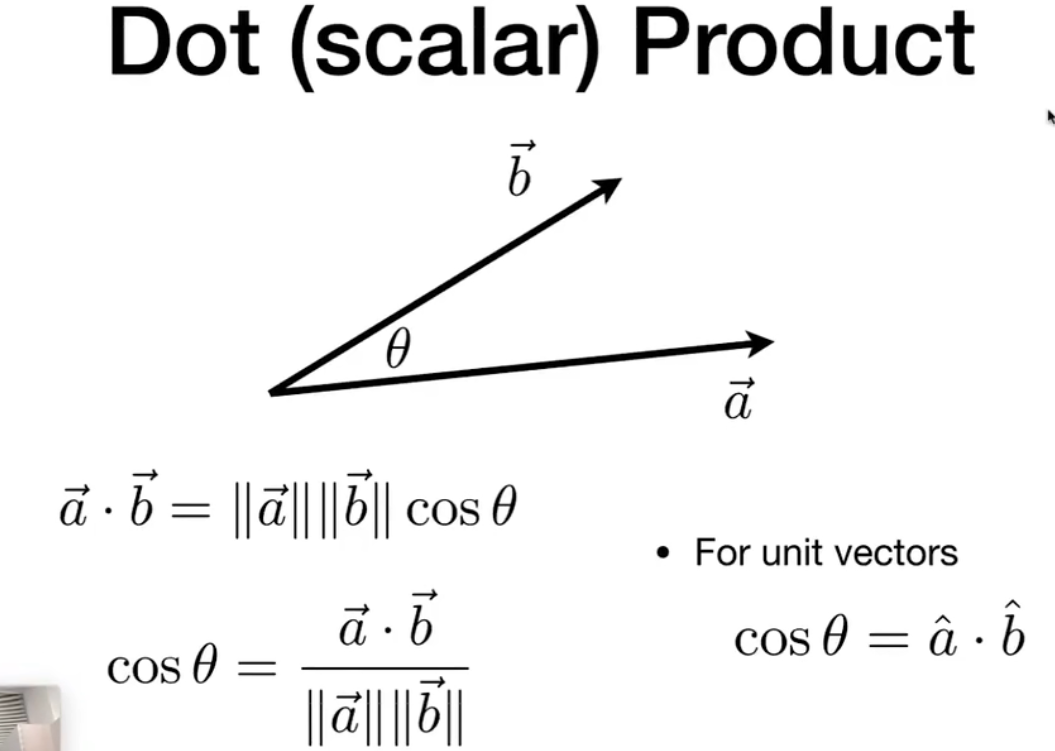
• 点乘: 符合 结合律/分配律/交换律

$$\begin{align} \vec{a} \cdot \vec{b} & = \vec{b} \cdot \vec{a} \\ \vec{a} \cdot(\vec{b}+\vec{c}) & = \vec{a} \cdot \vec{b}+\vec{a} \cdot \vec{c} \\ (k \vec{a}) \cdot \vec{b} & = \vec{a} \cdot(k \vec{b}) \end{align}$$

• 点乘还可以用于区分前后：

  

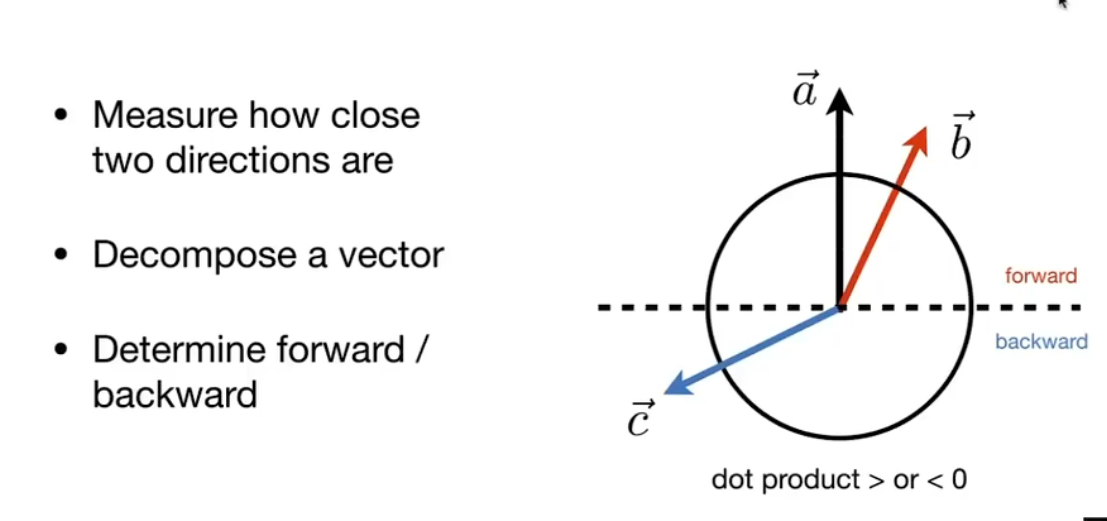
​ 例如 $\vec{b}，\vec{c}$ 和 $\vec{a}$做点乘，大于0说明在前方，小于0在后方

叉乘

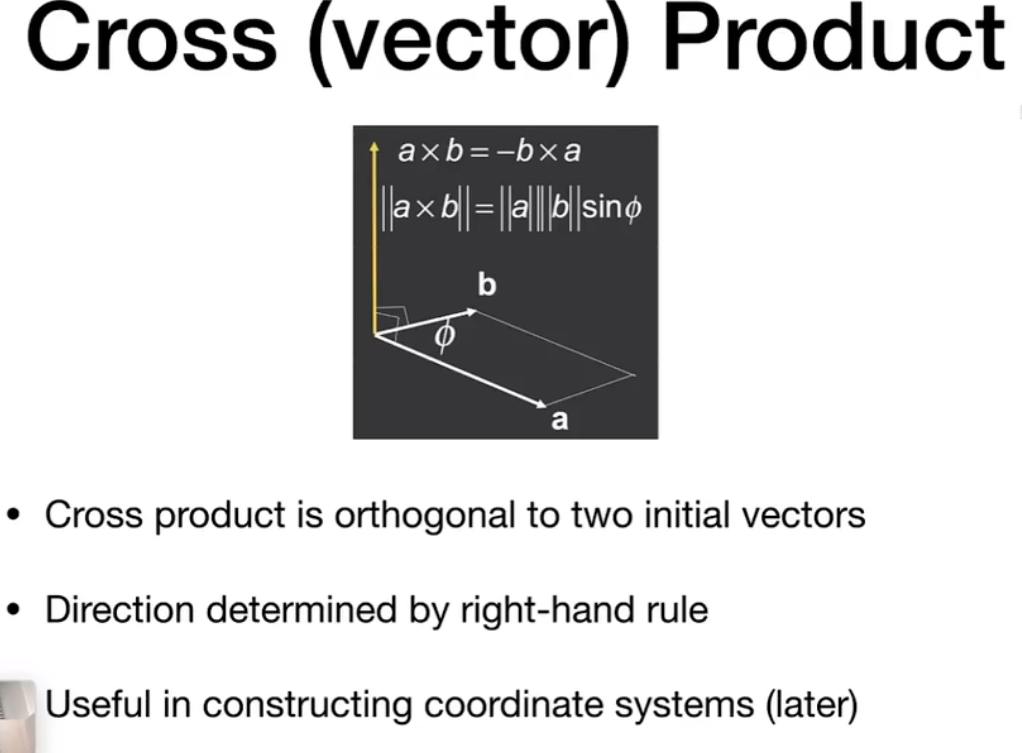
• 叉乘出的向量垂直于两个向量

• 方向：右手定则 (四指从$\bold{a}$绕到$\bold{b}$) 可依法向

• $$\begin{align} a \times b & = -b \times a \\ \|a \times b\| & = \|a\||b| \mid \sin \phi \end{align}$$

• 一个右手坐标系： $\bold{x} \cross\bold{y} = \bold{z}$

  一个左手坐标系： $\bold{x} \cross\bold{y} = \bold{-z}$

• 基本运算法则：自己叉乘自己是0向量，有分配律

  $$\begin{align} \vec{a} \times \vec{a} & = \overrightarrow{0} \\ \vec{a} \times(\vec{b}+\vec{c}) & = \vec{a} \times \vec{b}+\vec{a} \times \vec{c} \\ \vec{a} \times(k \vec{b}) & = k(\vec{a} \times \vec{b}) \end{align}$$

• 叉乘可以写成矩阵形式：

  

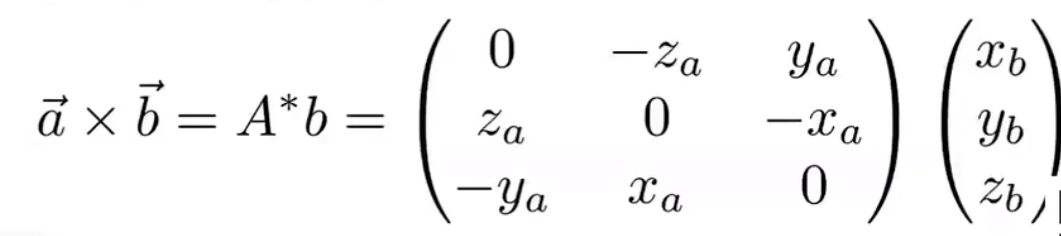
• 叉乘作用：

  • 判定左/右：

    

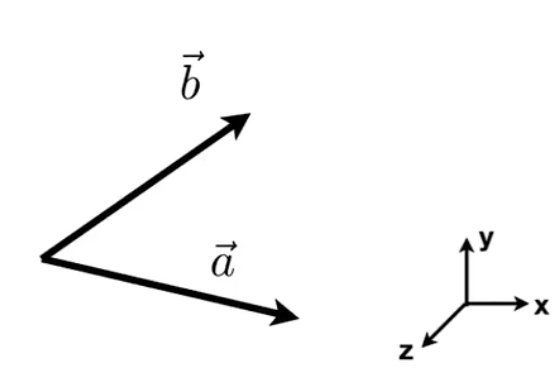
    如何判断$\bold{b}$是否在$\bold{a}$的左侧？ 用$\bold{a}\cross\bold{b}$即可，判断叉乘是否为正，若为正说明在左侧，反之在右侧。

  • 判断一个点是否在一个图形内部：

    

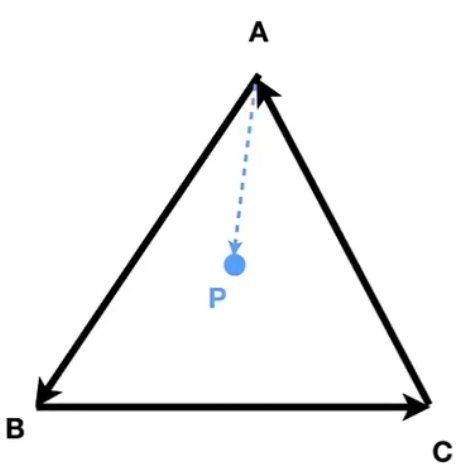
    用$\vec{AB}\cross\vec{AP}$ 若为正说明在$\vec{AB}$左侧，同理计算$\vec{BA}\cross\vec{BP}$ 和$\vec{CA}\cross\vec{CP}$ 发现都为正，那么说明这个点 $p$ 都在首位相接的向量的左侧，那么说明在这个首位相接向量构成的图形的内部。

    若这三条边是一个顺时针的呢？同理，会发现都在右边。

正交坐标系

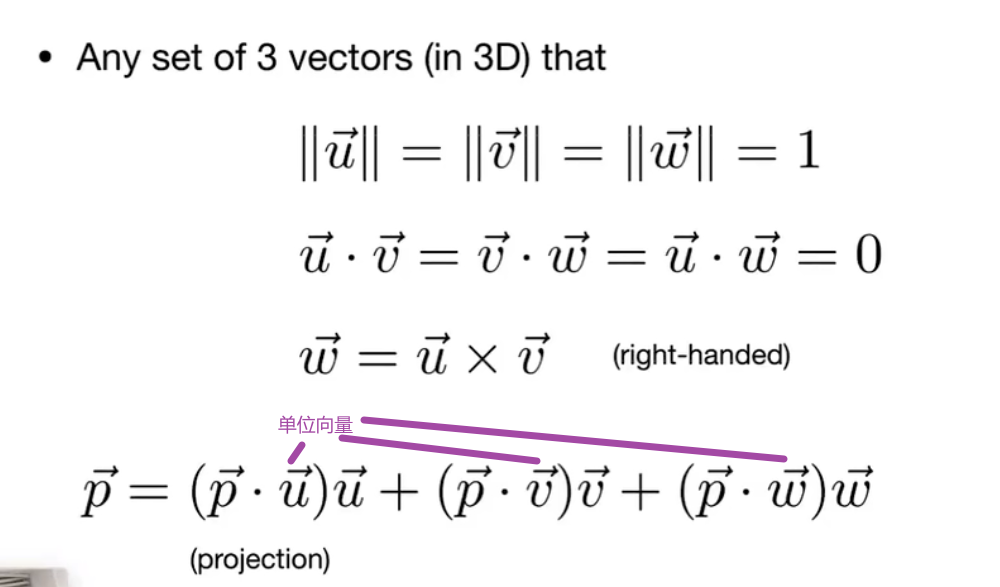
矩阵

矩阵乘法： 第一个矩阵的列数必须等于第二个矩阵的行数

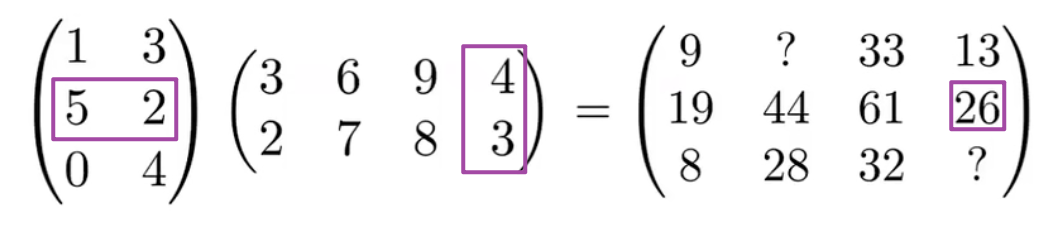
矩阵乘法不符合交换律， 符合结合律/分配律：

$$\begin{align} (A B) C & = A(B C) \\ A(B+C) & = A B+A C \\ (A+B) C & = A C+B C \end{align}$$

矩阵-向量乘法：

把向量当成一个$m*1$的矩阵即可

矩阵转置：

$$\begin{align} (A B)^{T} & = B^{T} A^{T} \end{align}$$

单位矩阵和逆矩阵：

$$\begin{align} I_{3 \times 3} & = \left(\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right) \\ A A^{-1} & = A^{-1} A = I \\ (A B)^{-1} & = B^{-1} A^{-1} \end{align}$$

点乘叉乘转换成矩阵形式：

Lec3: 变换Transformation

三维到二维投影：三维世界到二维平面

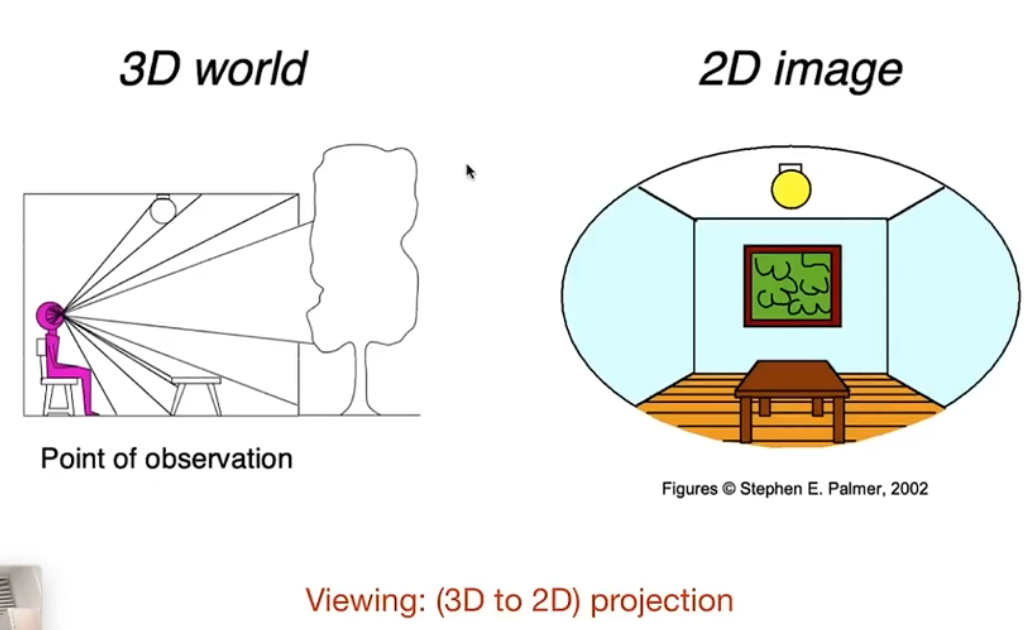
Scale Transform/尺度变换

均匀缩放：

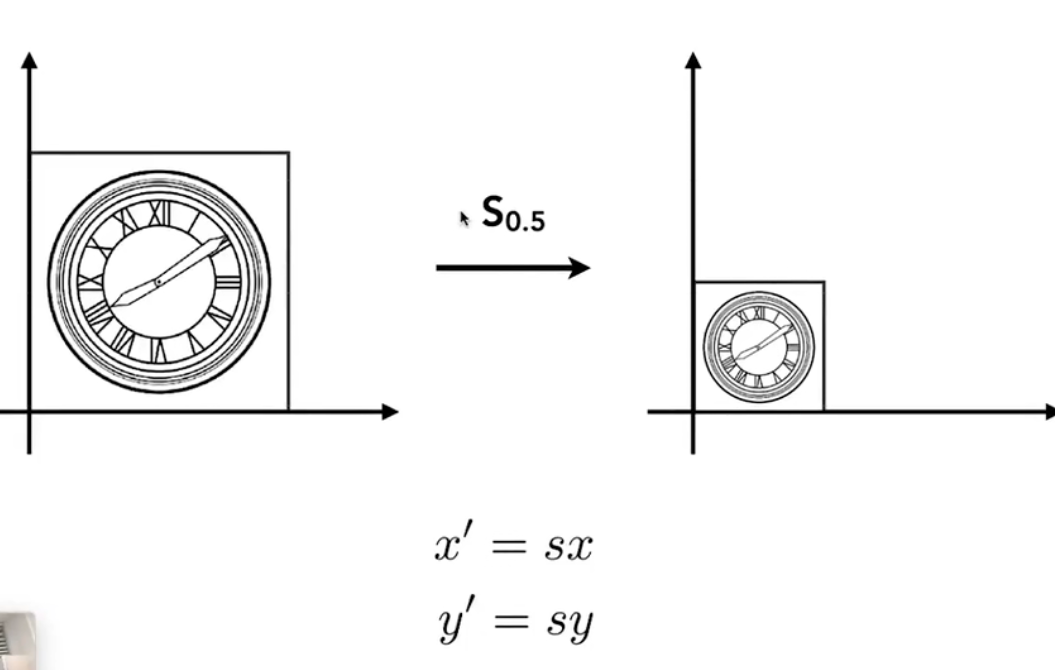
写成矩阵形式：

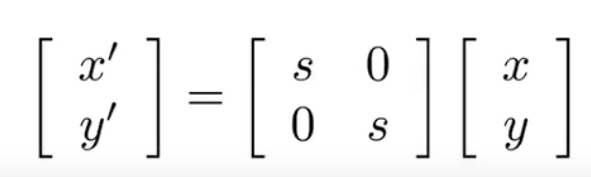
非均匀缩放：

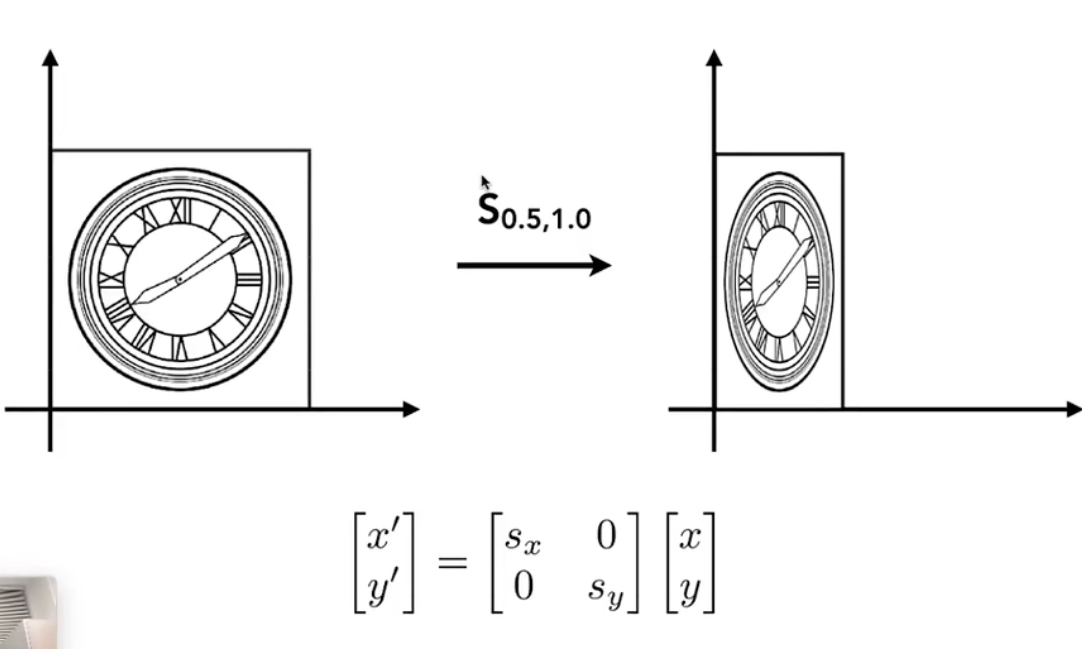
图像反转：

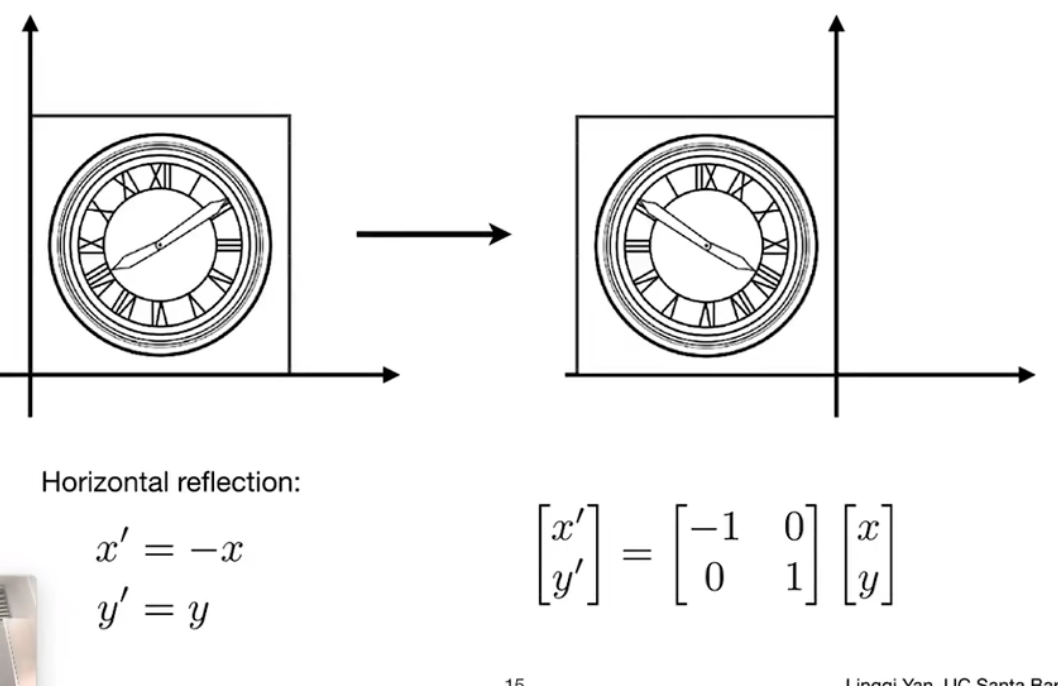
shear/错切变换 ：

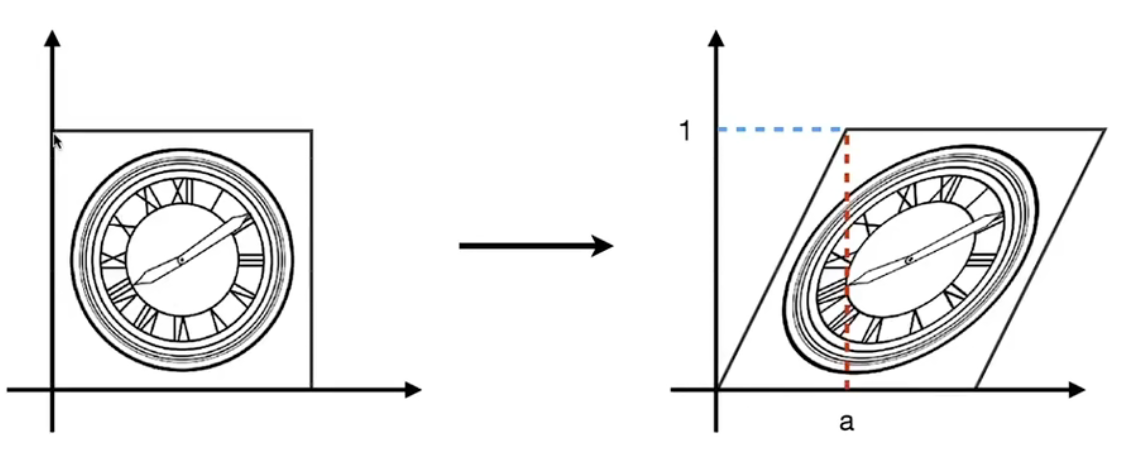
相当于y方向大小不变，向右拉扯。

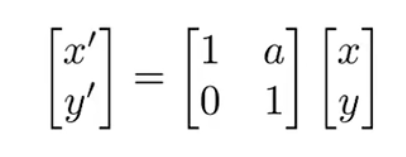
Rotate/旋转变换(逆时针旋转$\theta$)

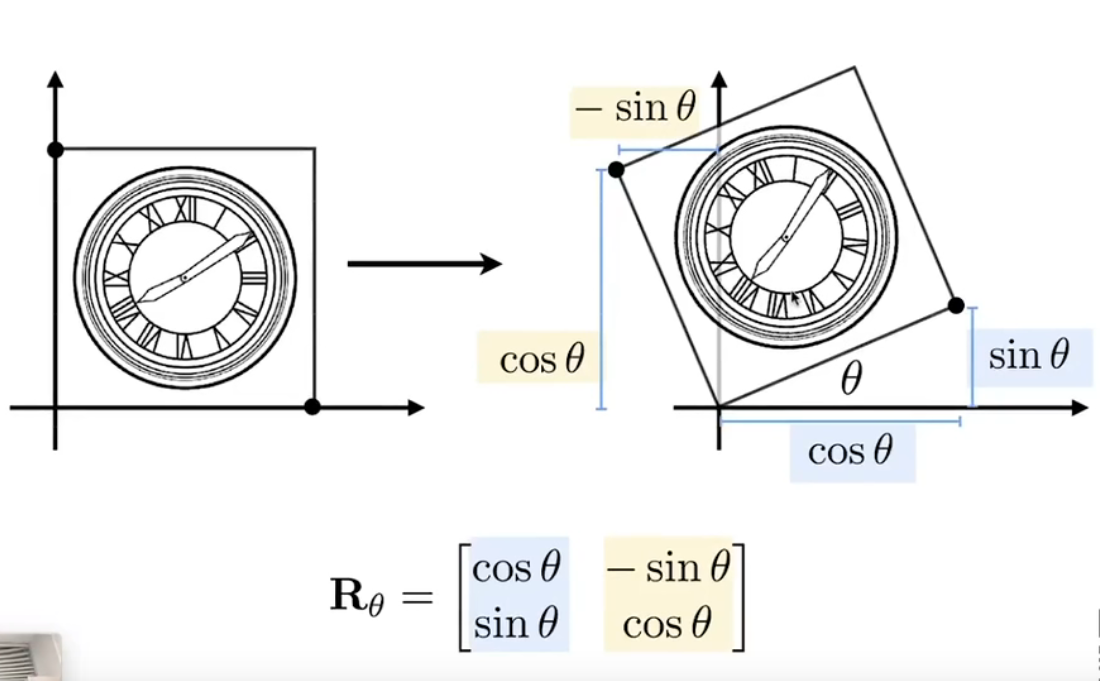
推导过程(下面推导是针对顺时针旋转$\theta$)：

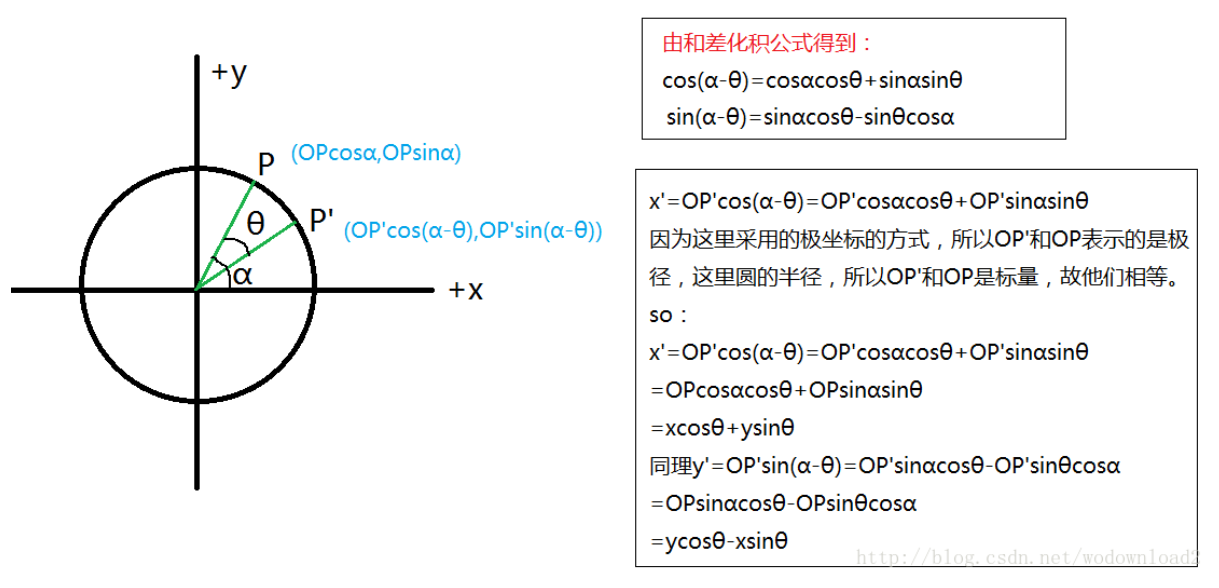
考虑顺时针旋转：顺时针旋转$\theta$相当于逆时针旋转$-\theta$，那么带入后会发现$\R{-\theta}$的结果就等于$R{\theta}^T$ 即顺时针旋转的逆矩阵。同时会发现

$$R_{\theta}^T = R_{\theta}^{-1}$$

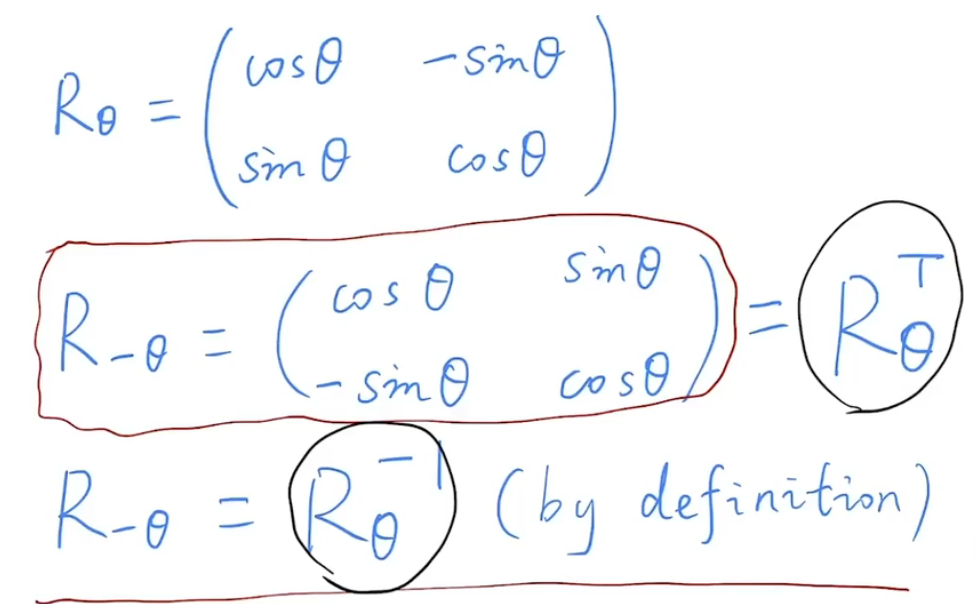
因此如果想让一个坐标顺时针旋转，左乘$R{\theta}^T $或者$ R{\theta}^{-1}$都是可以的。

homogeneous coordinates/齐次坐标

齐次坐标常用来做平移。

因为原来的二维矩阵乘坐标后总会含有x/y，无法表示一个常数项的偏移，不妨给变换矩阵加一个维度表示偏移。

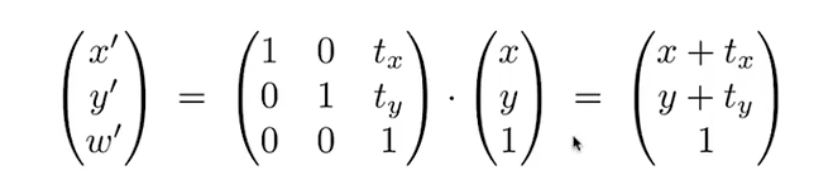
但是对于一个向量：由于它具有平移不变性，加的齐次坐标只能是0，为的是如果有一个向量也经过这个平移变换矩阵后不会影响他。

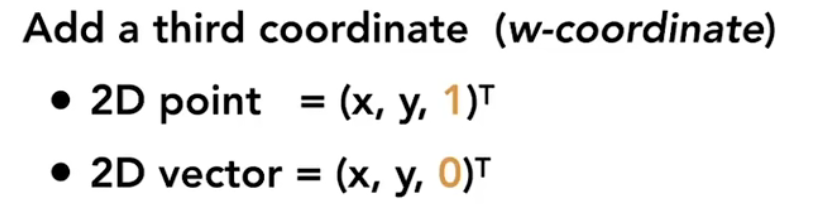
同时齐次坐标的做法还保证了下面的性质：

最后一个点+点一般认为是没意义的，我们也可以这么理解：

我们总是保证第三位的齐次坐标是1，那么点+点就是中点。

Affine Transformation/仿射变换

我们可以把以上总结为仿射变换：同时包含平移和缩放变换。

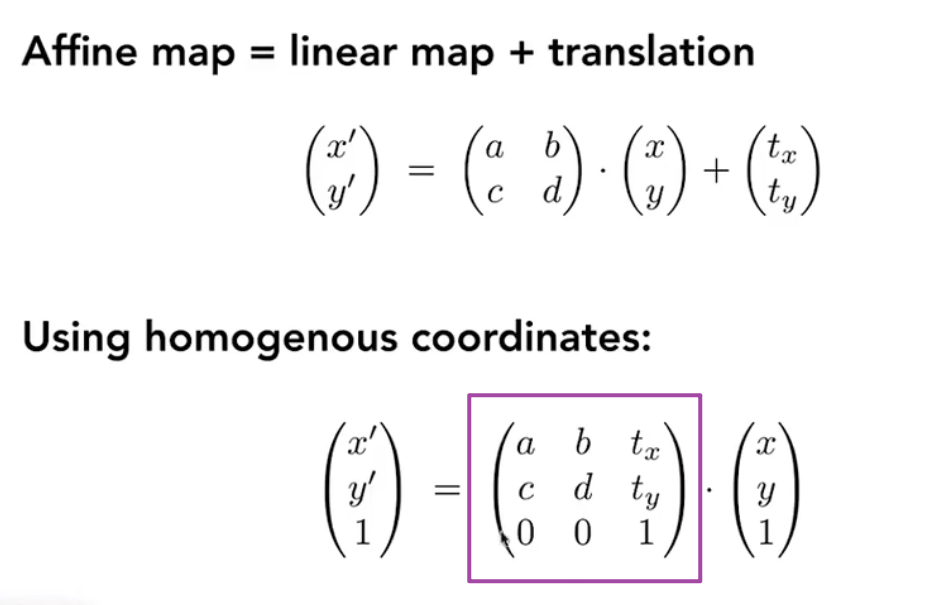
变换的顺序问题

先平移后旋转 和 先旋转后平移 是不同的(矩阵是不满足交换律的)。

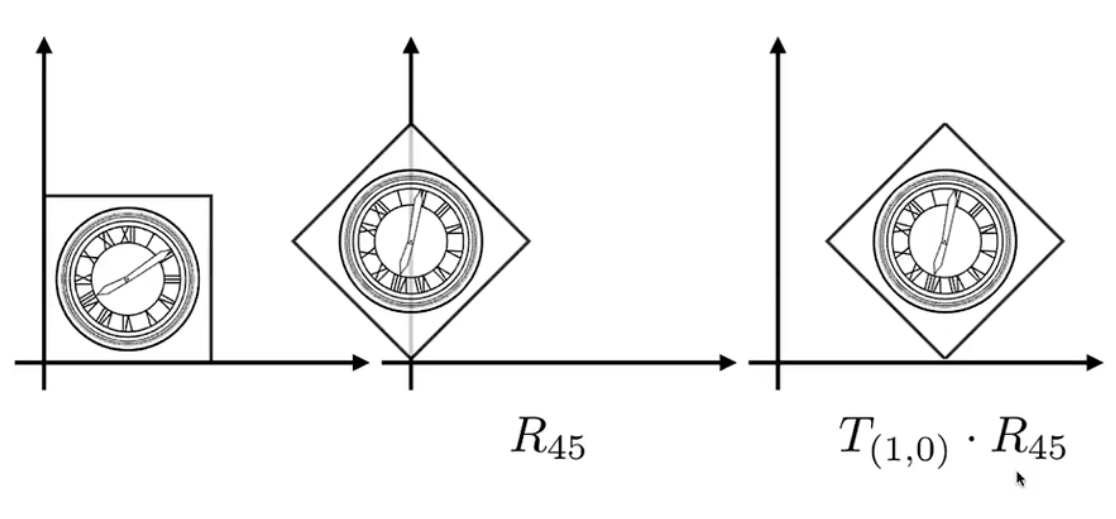
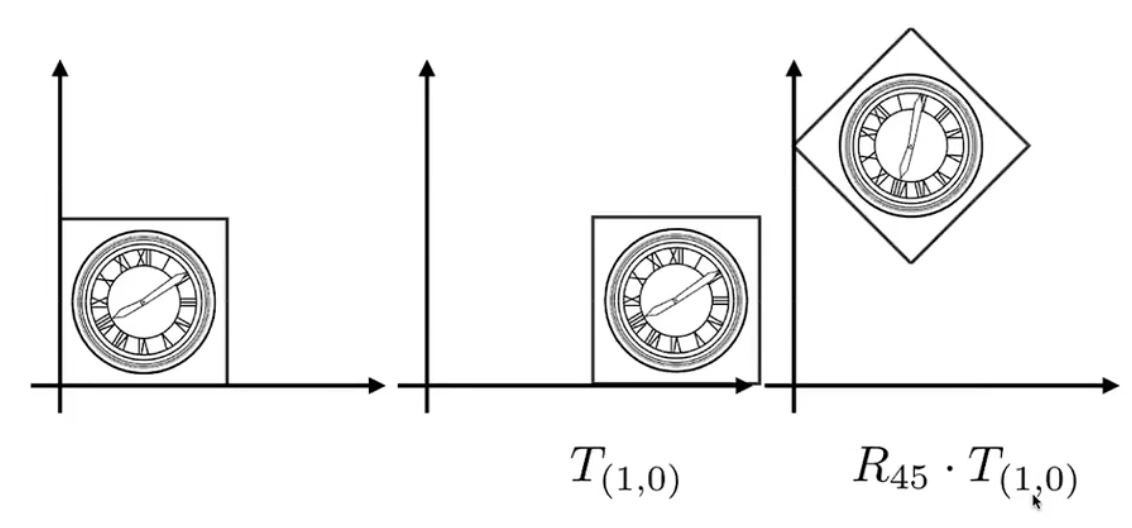
组合变换：

矩阵虽然没有交换律但有结合律：我们可以提前把$M = A_n…A_2A_1$先算出来，那么对于其他点也做同样的变换时：我们可以直接让他乘上这个矩阵，提高了效率。

分解变换：

组合变换的逆过程

假如我们希望绕原点旋转：首先需要移到原点，然后旋转，再移动回去。

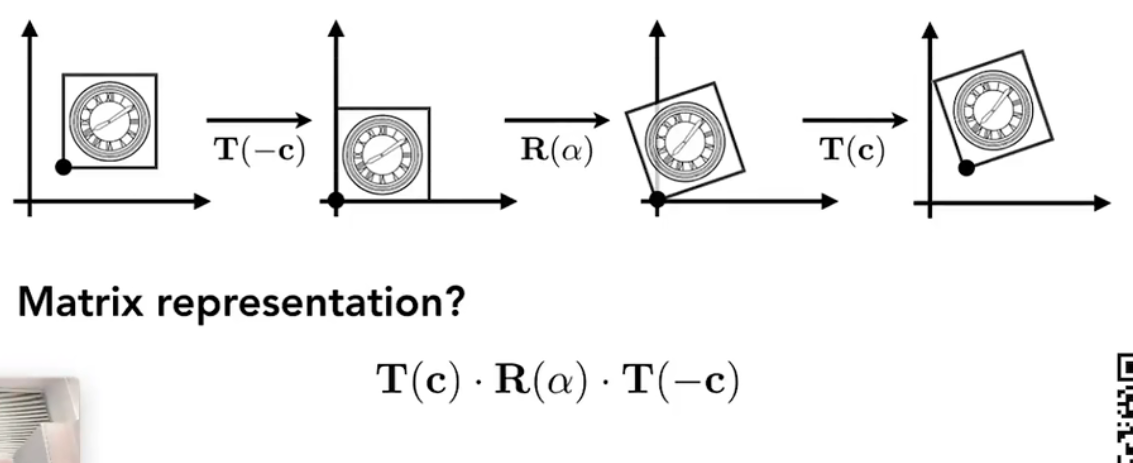
Lec4: Transformation Cont.

模型变换(modeling transformation)

3D transformation

和二维没有什么区别，多了一维$z$。

现在的仿射变换矩阵就是4*4的矩阵：

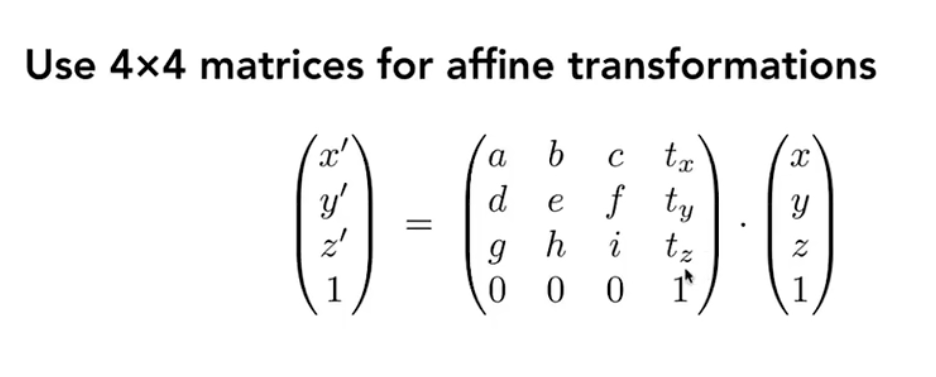
缩放和平移：

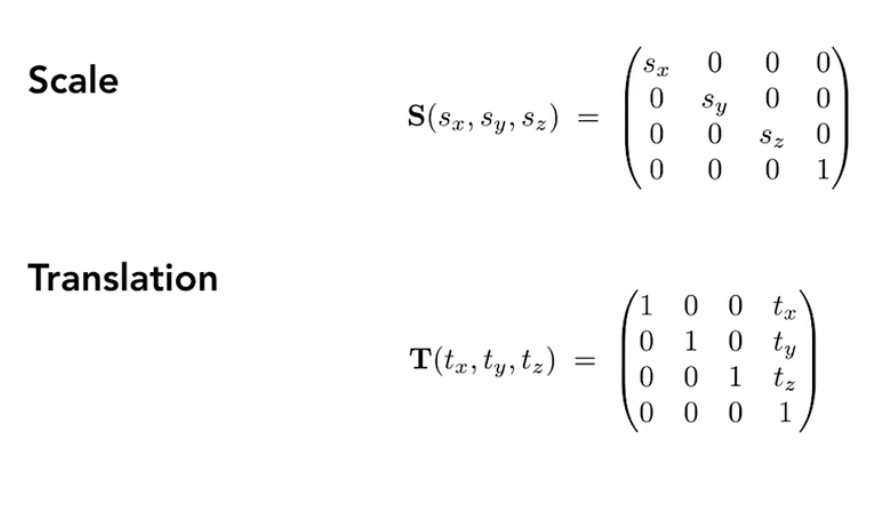
3D 旋转

一个旋转可以分解成三部分：绕x轴转，绕y轴转，绕z轴转。

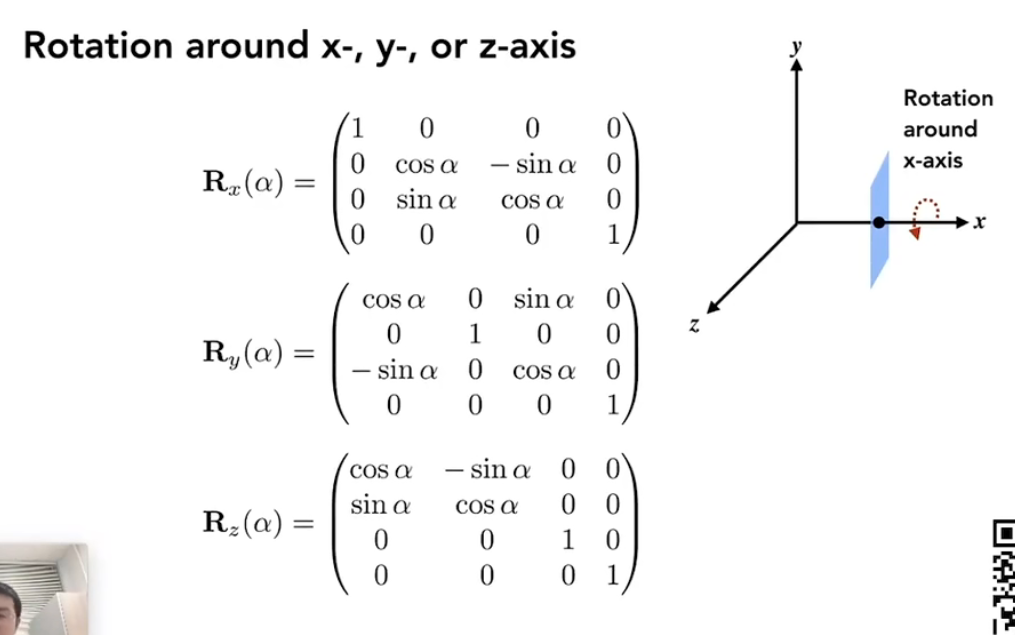
对于绕x，绕z，发现只需要把会动的对应坐标轴对应写成二维旋转的形式即可。

但是对于绕y轴旋转会发现，他对应的矩阵中包含$\alpha$的地方都变成了相反的(观察橙色部分)。

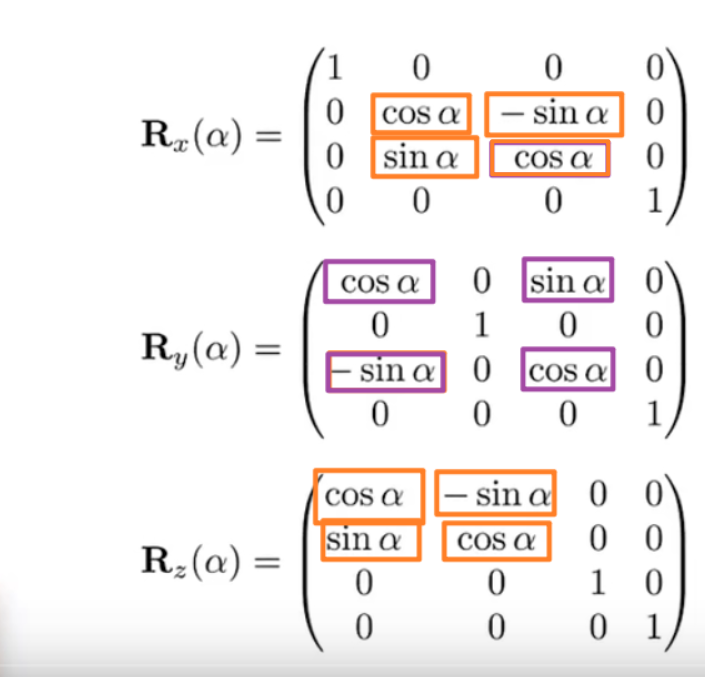
但这是正确的，通过右手螺旋定则发现:

• 绕$x$轴转动时，$y \cross z$的方向就是$x$的方向
• 绕$z$轴转动时，$x \cross y$的方向就是$z$的方向
• 而绕$y$轴转动时，$x \cross z$的方向却是$-y$的方向，因此想要逆时针转应该加上转置或者取逆。

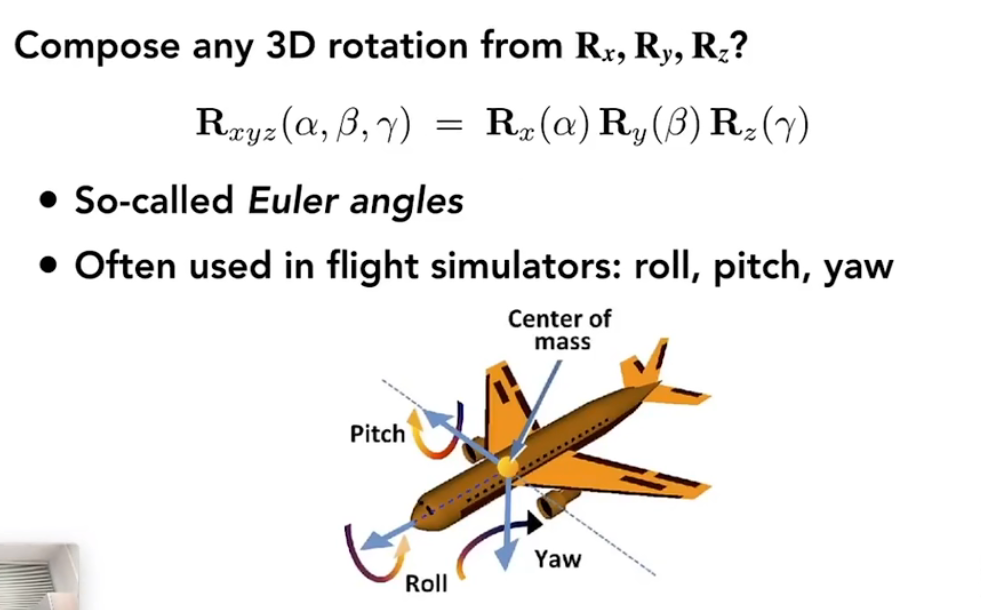
因此:

• 任何一个旋转都可以看成绕$x$轴转，绕$y$轴转，绕$z$轴转的合成.

• $\alpha,\beta,\gamma$叫做欧拉角

罗德里格斯旋转公式：

我们还有一种常用的方式是：绕着某一个轴旋$\bold{n}$转一个角度$\alpha$，这会利用到罗德里格斯旋转公式。(在这里我们默认旋转轴过的是原点)

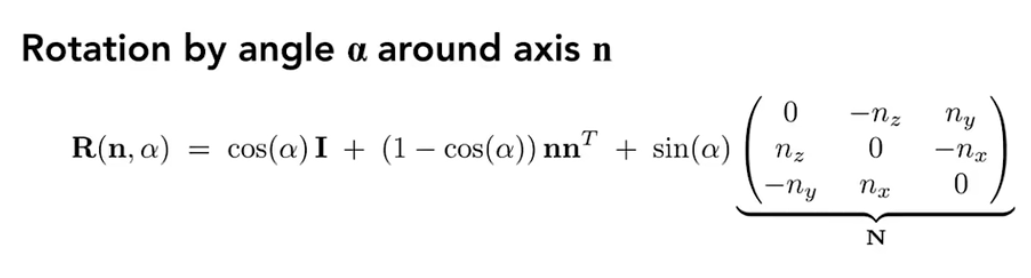
如果有需要让他绕着非过原点的旋转轴怎么办？ 先平移再旋转再平移回来即可。

相机变换(Camera transformation)

这一部分本质就是找一个位置放置照相机。

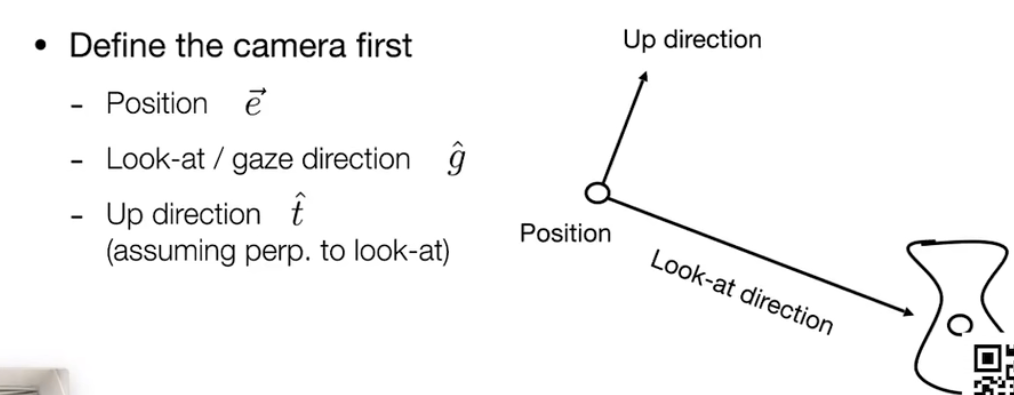
因此我们需要这几个要素：

• 相机的位置 $\vec{e}$
• 向哪儿里看 $\hat{g}$
• 相机向上朝向的方向 $\hat{t}$ （注意有相机位置和朝向后并不能确定的排除一个照片，因为相机还可以绕着$\hat{g}$旋转，造成找出的照片角度不同）

首先我们规定一个相机标准位置：位于原点，相机上方方向为$y$轴，相机朝向为$-z$方向。

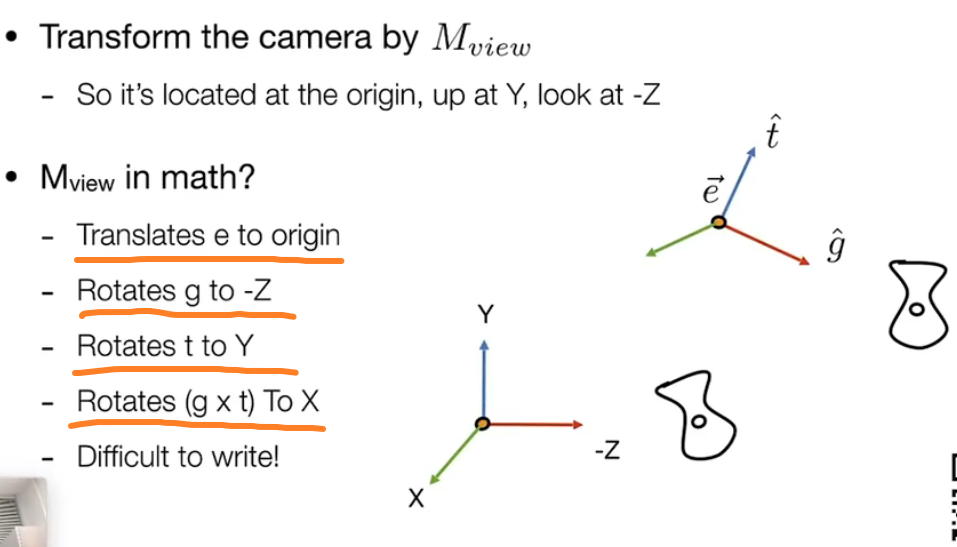
其中前三部做到，第四步就自然而然做到了，因此我们只需要对前三部操作即可。下面考虑把以上这些操作写成一个矩阵：

• 首先需要移到原点：

  

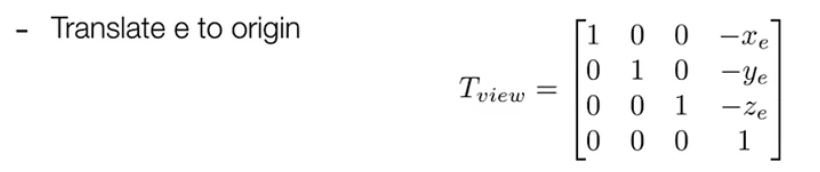
• 随后需要做旋转，把一个向量旋转到 $-z$或是$y$都是不容易的，不妨考虑他的逆过程，从$x$轴到$g\cross t$ ，$y$轴到$t$，$z$轴到$-g$ 是有公式可用的，即$R_{view}^{-1}$ 。

  这里的$R_{view}^{-1}$ 怎么得来的呢？

  我们希望把向量$x(1,0,0,0)$ 向量$y(0,1,0,0)$ 向量$z(0,0,1,0)$ 转移到 $t,-g,g × t$构成的新坐标系。简单来说我们希望：从$x$轴到$g\cross t$ ，$y$轴到$t$，$z$轴到$-g$ 的映射被矩阵$R{view}^{-1}$表达出来，我们可以把向量$x(1,0,0,0)$ 向量$y(0,1,0,0)$ 向量$z(0,0,1,0)$ 左乘$R{view}^{-1}$发现：得到的正好是对应的新轴的x的坐标。下面我举个例子，以x:$(1,0,0,0)^T$为例，左乘$ R_{view}^{-1} $得到：

  $$\left(x_{\hat{g} \times \hat{t}}, y_{\hat{g} \times \hat{t}}, z_{\hat{g} \times \hat{t}}\right)$$

  说明这个旋转矩阵可以把x向量经过旋转成为了$g\cross t$ 向量，也就是我们希望对应上的向量。我们可以发现这种旋转矩阵的构造十分自然美妙。

  在上一节提到了旋转矩阵的逆矩阵等价于转置矩阵，因此$R{view}$ 等价于 ${R{view}^{-1}}^T$ 。

  

到此完成了基本的视图变换。

投影变换(projection transformation)

透视投影 vs. 正交投影：

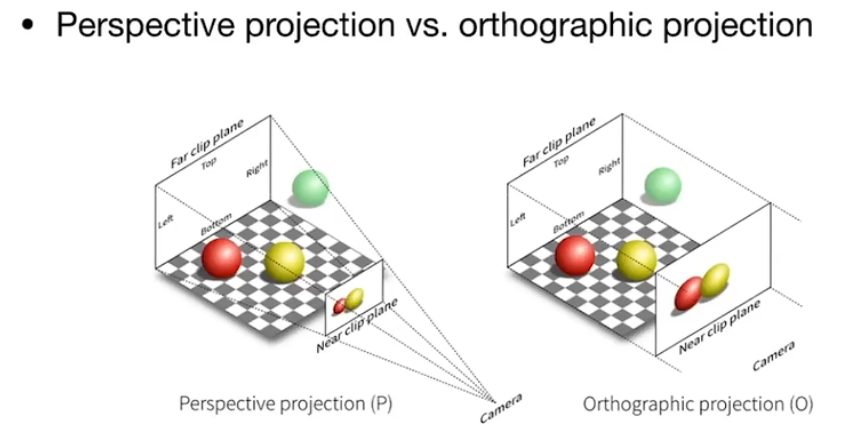
我们看左图的透视投影，远近不同，球大小也有区别，而正交投影没有这个特点。

正交投影

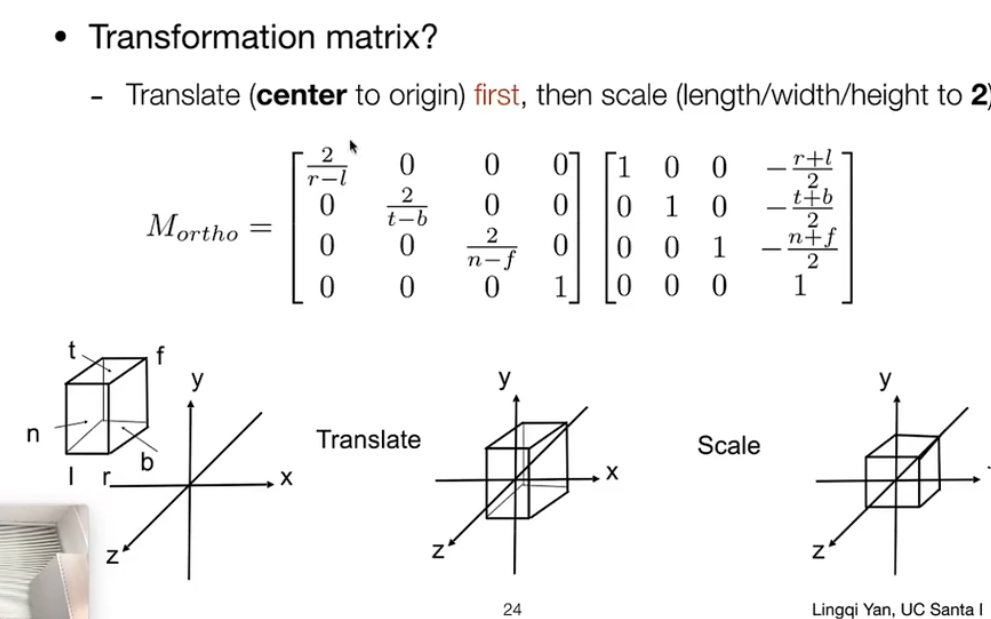
如何做一个正交投影？

• 平移到原点
• 尺度变换：缩小长高宽到2，这样可以使得一个长方体变成$[-1,1]^3$的标准立方体。

透视投影

一组平行线在透视投影中是可能相交的：

怎么做透视投影？

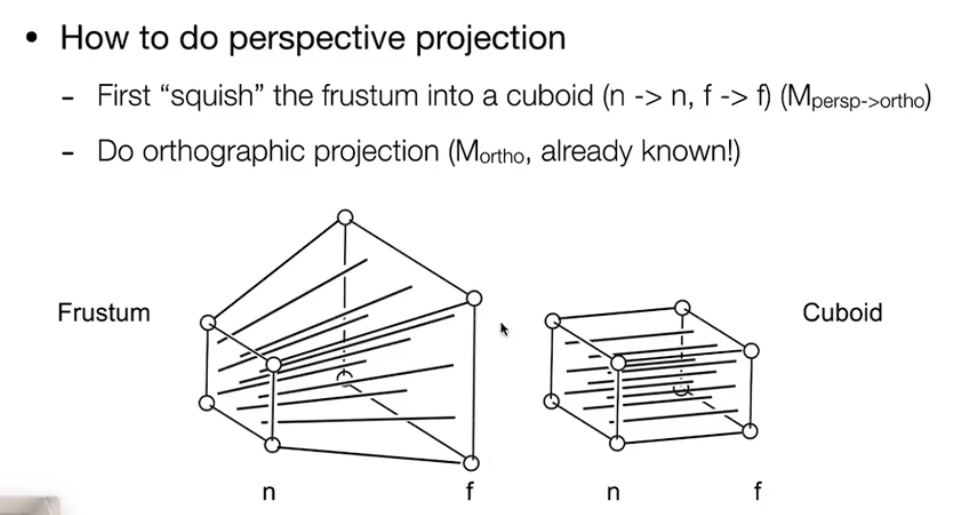
• 把截头锥体压扁成一个长方体
• 做正交投影

正交投影我们会做，那么现在只需要如何压扁一个截头锥体：

不妨先考虑在$yz$平面上如何变化：

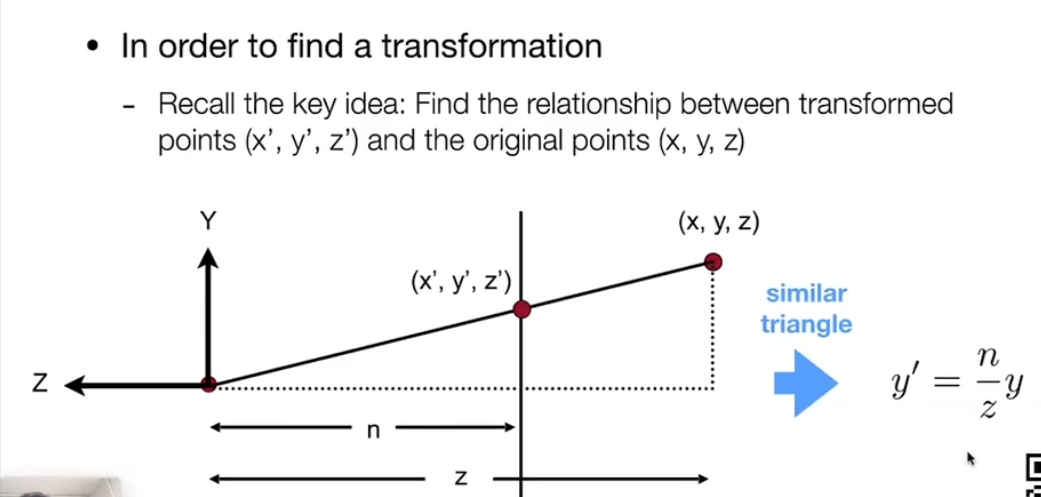
同理在$xz$平面上也是这样：

因此我们直接分别对x和y进行变换压缩至x’,y’处(注：此时z轴变换暂时不考虑)：

那么什么矩阵可以做一个这样的变化呢？我们设这个矩阵为$M_{persp \to ortho}$, 即希望找出下面这样的一个矩阵：

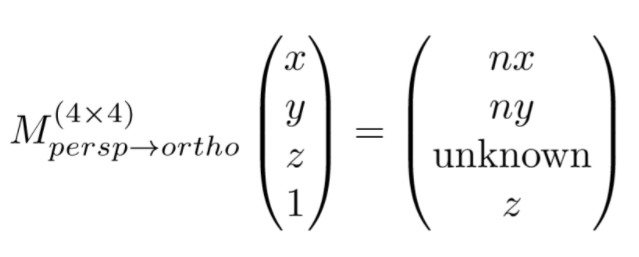
这个矩阵的1，2，4行是很容易确认的，即：

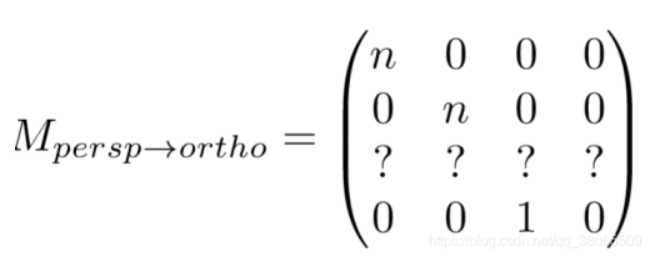
现在只需填上第三层即可，透视投影的一个特性是：截头锥体的前后面变换之后z坐标不变，因此我们可以找出两个特殊的点：

• 近平面上任何一点通过投影变换后z坐标不会变(即坐标(x,y,n))
• 远平面上任何一点通过投影变换后z坐标不会变(即坐标(x,y,f))

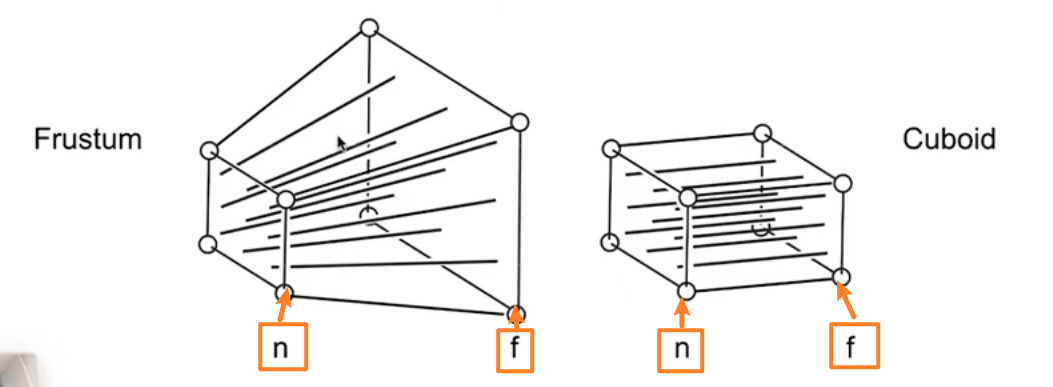
我们希望 坐标(x,y,n) 变换后的z轴还是n：

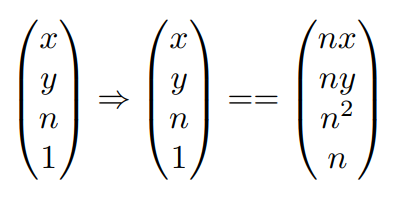
只需要让$M_{persp \to ortho}$ 的第三行符合下式(0 0 A B)的形式，并满足和近平面坐标相乘后等于$n^2$：

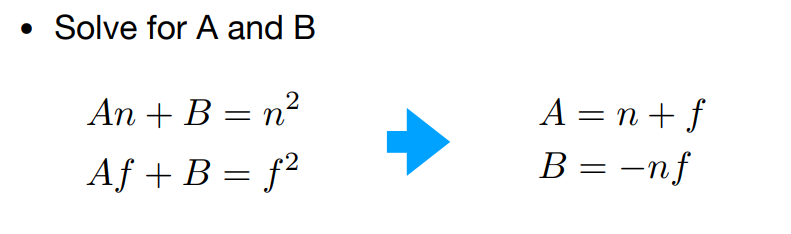
但此时AB还是没有具体求出来，不妨再考虑一下原平面，同理得到：

因此就可以解出AB分别为：

那么现在做透视投影就可以直接这么运算： 先将透视投影转换为正交投影，然后再做正交投影。

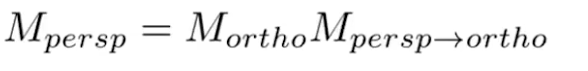
在透视投影转正交投影的变换中有个反常识的现象： 也就是截头锥体的中间一点(x,y,z) 其中f>z>n, 这样的一点在经过透视投影转正交投影变换矩阵时，会变得更加接近f面, 更远离n，也就是变换后的坐标回会比z更小。证明如下：

0~VJ@7QRIZ%X{}RS9KK.png)

视口变换(ViewPort Transformation)

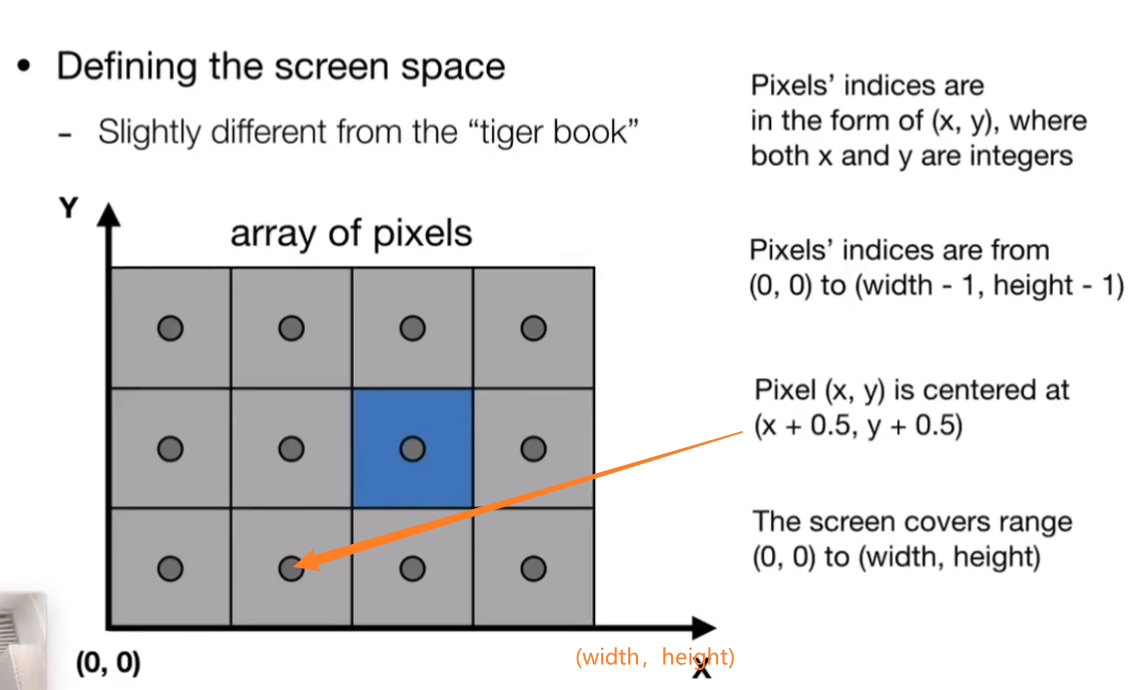
我们希望把$[-1,1]^3$的拉伸成$[0, width]×[0,height]$,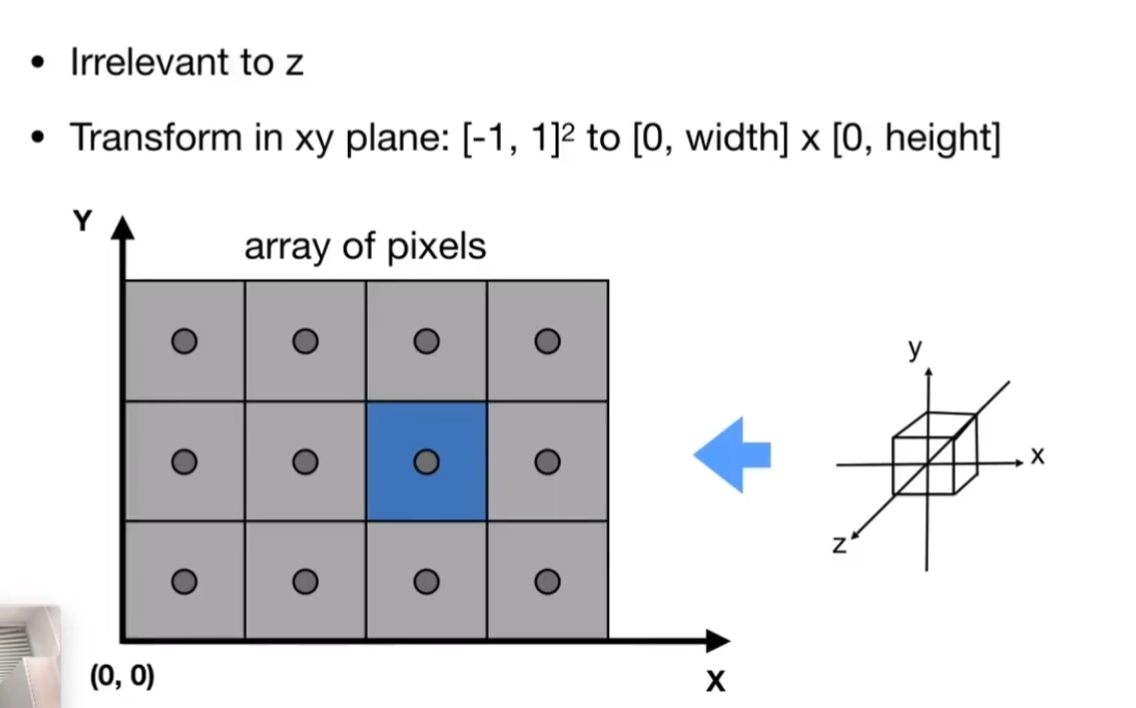

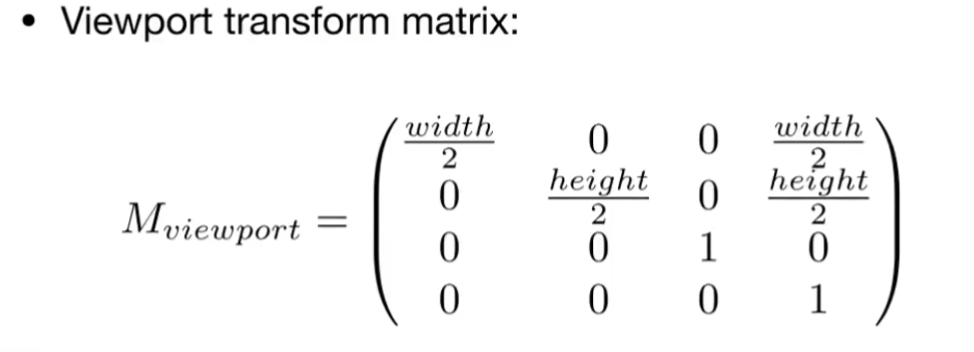
我们直接做scale+偏移：宽度上原来是-1，1扩大到$[-width/2，+width/2]$, height同理，同时我们还需要做完后做一个偏移，让范围变到$[0,width]*[0,height]$