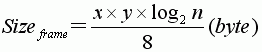AHU计算机图形学笔记
AHU计算机图形学
写在前面:
对AHU计算机图形学课的一些笔记总结,我自认为总结的还算全面,期末靠着这个复习也拿到了相对不错的分数,但受限于个人水平,有些地方可能会出现错误,如果有什么遗漏或者错误之处,可以发邮件到:howiewang.cs@gmail.com
像素:绘图的最小单位。
分辨率与像素的关系:若分辨率1024*768(每行有1024个像素,总共有768行)。
第一章:绪论
计算机图形学(Computer Graphics)是研究怎样利用计算机来显示、生成和处理图形的原理、方法和技术的一门学科。国际标准化组织(ISO)定义它为:计算机图形学是研究通过计算机将数据转换成图形,并在专门显示设备上显示的原理、方法和技术。
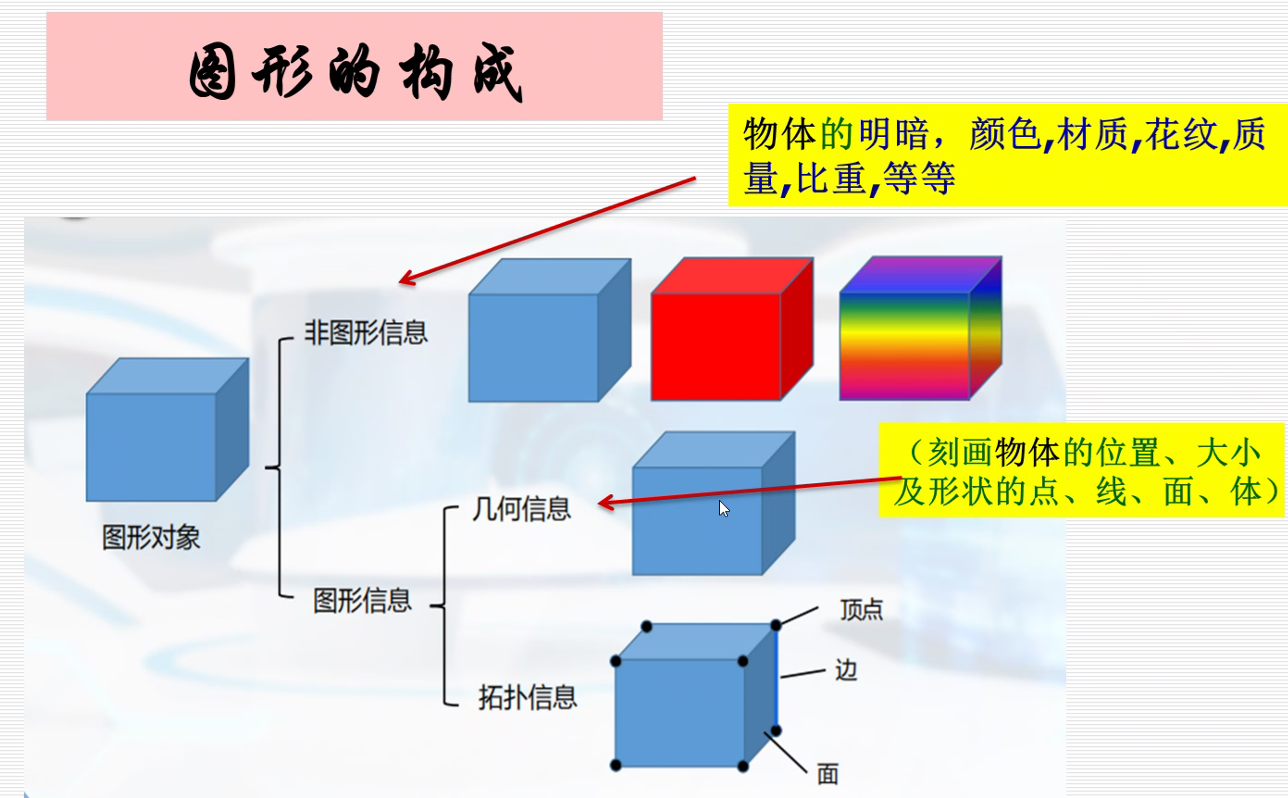
计算机中表示带有颜色及形状信息的图和形常用两种方法:点阵法和参数法。点阵法是用具有灰度或颜色信息的点阵来表示图形的一种方法,它强调图形由哪些点组成,并且具有什么灰度或色彩。参数法是以计算机中所记录图形的形状参数与属性参数来表示图形的一种方法。形状参数可以是形状的方程系数、线段的起点和终点对等几何属性的描述;属性参数则描述灰度、色彩、线型等非几何属性。这样,可以进一步细分:把参数法描述的图形叫做图形(Graphics),而把点阵法描述的图形叫做图像(Image)。
图形学的发展:
- 酝酿期(20世纪50年代)
1950年,美国麻省理工学院(MIT)的旋风1号(Whirlwind I)计算机配备了阴极射线管(CRT)来显示一些简单的图形。
1958年,美国CALCOMP公司将联机的数字记录仪发展成滚筒式绘图仪,GERBER公司则把数控机床发展成平板式绘图仪。
整个50年代,计算机图形学处于准备和酝酿时期,称之为“被动”的图形学。 - 萌芽期(20世纪60年代)
60年代初,美国麻省理工学院林肯实验室中基于旋风计算机开发的北美空中防御系统SAGE具有了指挥和控制图形对象的功能。
1962年,美国麻省理工学院林肯实验室的Ivan.E.Sutherland发表了一篇题为”Sketchpad:一个人——机通信的图形系统”的博士论文,其中首次使用了“Computer Graphics”这个术语,从而确立了计算机图形学的学科地位。 - 发展期(20世纪70年代)
70年代,美国洛克希德飞机公司完成了一个用于飞机设计的交互式图形处理系统,即CADAM。
计算机图形处理技术进入实用化阶段,但由于图形设备昂贵、功能简单、基于图形的应用软件缺乏等原因,计算机图形学还是一个较小的学科领域。 - 普及期(20世纪80年代)
由于出现了带有光栅图形显示器的个人计算机和工作站,以及大量简单易用、价格便宜的基于图形的应用软件,计算机图形学进入了社会生活的各个领域。 - 提高增强期(20世纪90年代)
计算机图形学向着标准化、集成化和智能化方向发展。
第二章:计算机图形系统及硬件
计算机图形系统概述
一个交互式计算机图形系统应具有计算、存储、交互(对话)、输入和输出等五个方面的功能
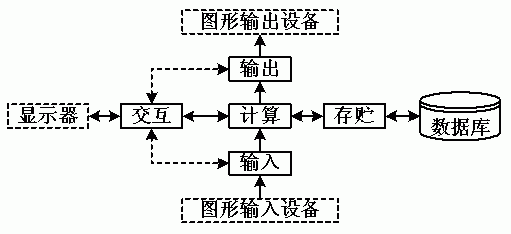
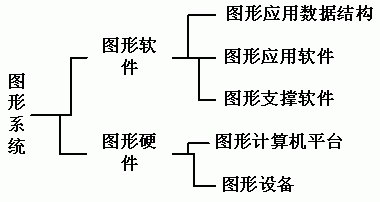
计算机图形系统结构:
图形应用数据结构:对应一组图形数据文件,保存着图形对象的全部描述信息。
图形应用软件:是图形系统的核心部分,包括了各种图形生成和处理技术,是图形技术在各种不同应用中的抽象。
图形支撑软件:由一组公用的图形子程序所组成,它扩展了系统中原有高级语言和操作系统的图形处理功能。
图形应用数据结构对应一组图形数据文件,存放将要生成的图形对象的全部描述信息(位置、大小、属性、…….)
图形应用软件是解决某种应用问题的图形软件.它从图形应用数据结构中取得物体的几何模型和属性等,按照应用要求进行各种处理(裁剪、消隐、变换、填充等),然后使用图形支撑软件所提供的各种功能,生成该对象的图形并在图形输出设备上输出。
图形支撑软件一般由一组公用的图形子程序组成。
图形输入设备
1.键盘
2.鼠标
3.光笔
4.操纵杆
5.触摸屏
6.跟踪球/空间球:
跟踪球是一个球,可用手指或掌心旋转以使屏幕光标移动,常用作二维定位设备。空间球与跟踪球不同的是它可以提供6个自由度,常用作三维定位和选择设备。
7.数字化仪:
数字化仪用来输入一组坐标位置,相互以直线段连接,以逼近曲线或表面形状。
8.扫描仪
什么是 阴极射线管(CRT)?
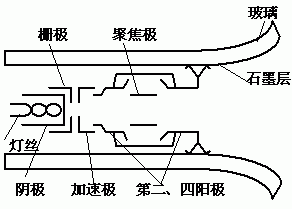
阴极射线管(CRT,Cathode Ray Tube)利用电磁场产生高速的、经过聚焦的电子束,偏转到屏幕的不同位置轰击屏幕表面的荧光材料而产生可见图形。
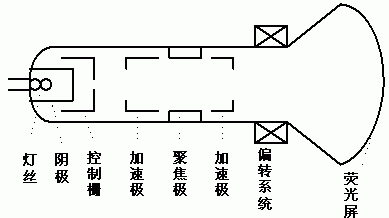
(1)电子枪:
控制栅:控制电子的数量
加速极:控制电子的速度
聚焦极:把电子聚集成一束电子
(2)偏转系统:
分为电偏转和磁偏转两种,电偏转有两组电极板,水平偏转板和垂直偏转板。
电偏转: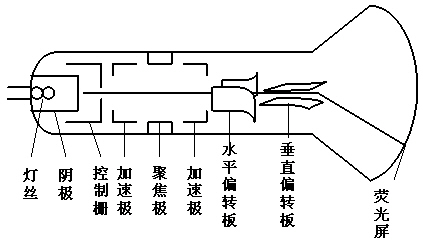
磁偏转: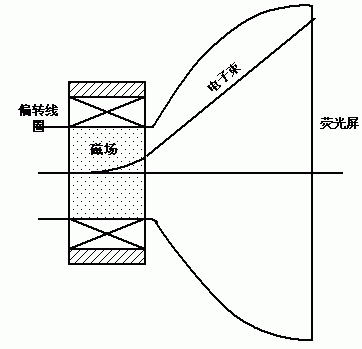
(3)荧光屏:
主要结构:三色荧光屏、三支电子枪、荫罩板。
三色荧光屏:在整个荧光屏上密密麻麻交错布满了能发R、G、B光的荧光小点,这些荧光点按次序整齐的排列,并相互错开,如下图所示。
三支电子枪:荫罩管的尾部装有三支电子枪,它们安装成“品”字形,互成120度角,并略向管轴倾斜,以保证三支电子枪能同时击中一组荧光小点。
每只电子枪只能控制开或者关(2种强度):22\2=8种颜色
每只电子枪可控制8种强度:88\8=256种颜色
每只电子枪能控制256种强度:256*256*256种颜色
荫罩板:在离开荧光屏1cm处安装了一块薄钢板制成的网板,像一个罩子将屏幕罩起来,故称荫罩板。荫罩板上有许多小孔,每个小孔准确地和一组三色荧光小点对应。这样,三支电子枪正好交汇在荫罩的小孔上,然后再各自打在相应的荧光小点。
CRT图形显示器
1.随机扫描的图形显示器
随机扫描的图形显示器又称向量显示器或笔划显示器,电子束的定位和偏转具有随机性,即电子束的扫描轨迹随显示内容而变化,只在需要的地方扫描,而不必全屏扫描(可局部扫描)。
荧光粉余晖时间短,荧光粉发光后马上消失,然后再重复这样的过程,刷新频率低画面会一闪一闪,刷新频率过高会高频度打击屏幕,可能会击穿或者烧毁。
随机扫描显示器的特点
(1)无冗余扫描、速度快、图像清晰、比光栅系统具有更高的分辨率,生成光滑线条。
(2)不能显示逼真场景,和电视标准不一致,驱动系统也较复杂。
2.直视存储管图形显示器
直视存储管(DVST,direct-view storage tube) 从表面上看直视存储管的特性极象一个有长余辉的荧光屏,一条线一旦画在屏幕上,在一小时之内都将是可见的。
不能局部修改,不能显示彩色。
3.光栅扫描的图形显示器
扫描过程:如下图所示,在光栅扫描系统中,电子束横向扫描屏幕,一次一行,从顶到底顺次进行,当电子束横向沿每一行移动时,由电子束的强度不断变化来建立亮点的图案。
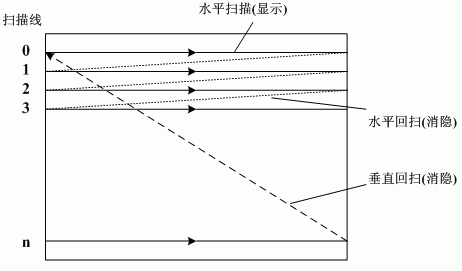
刷新速率:每秒扫描的帧数。
水平回扫:每条扫描线扫过后,电子束返回到屏幕左端,称为电子束的水平回扫。
垂直回扫:在每一帧的终了,电子束返回的屏幕左上角,称为电子束的垂直回扫。
逐行扫描和隔行扫描:逐行扫描是扫描线从屏幕顶端开始,从0行光栅开始,逐行下扫,直到屏幕底部;隔行扫描将每帧显示分为两趟,采用隔行刷新方式。第一趟,电子束从顶到底,一行隔一行扫描偶数扫描线,垂直回扫后,电子束则进行第二趟扫描奇数扫描线。隔行扫描使在逐行扫描所需时间的一半时就能看到整个屏幕显示。
在光栅扫描的图形显示器中,被显示的线段、字符、图形及其背景色都存储在刷新缓冲存储器(Refresh Buffer)或称 帧缓冲存储器(Frame Buffer,FB)中,刷新缓冲存储器保存的每一组信息对应屏幕上的一个点。
像素(pixel或pel,是picture element的简写):每个屏幕点称为一个像素。像素信息从应用程序转换并放入帧缓冲区的过程称之为扫描转换过程。
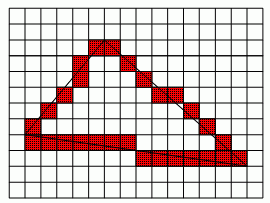
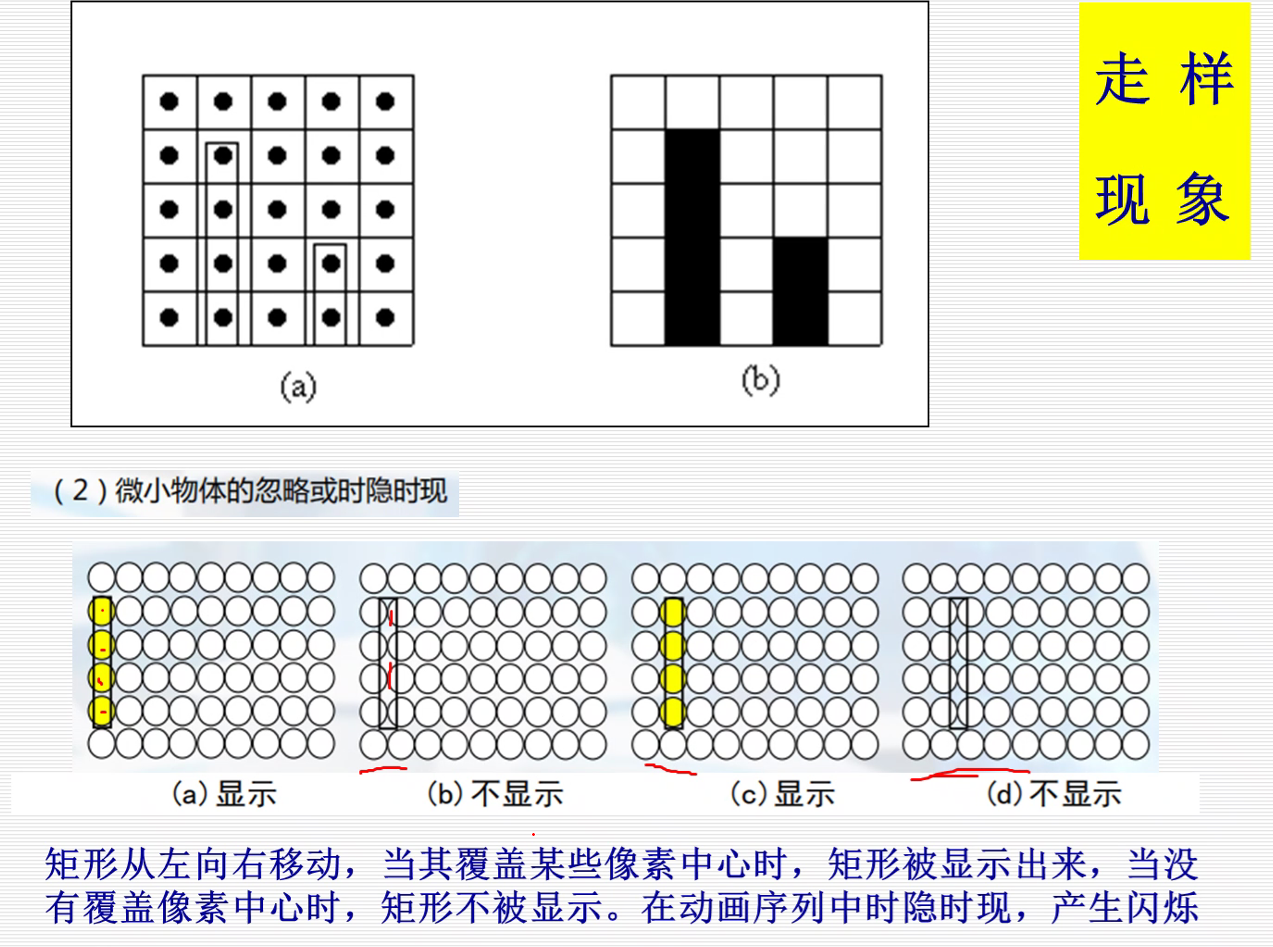
走样:光栅扫描的图形显示器是画点设备,绘制图形时只能用尽可能靠近图形的像素点集来近似表示图形,因而会产生失真。这种失真称为走样。
如下图就是走样现象:原因就是像素点是离散的,只能近似表示图形。
平板显示器
平板显示器(flat-panel display) 是一种低电压、轻小型、数字化显示器件,它可以分为发射显示器和非发射显示器两类。
发射显示器(emissive display):将电能转换为光能,如等离子体显示器。
非发射显示器(none-emissive display):利用光学效应,将太阳光或来自其他光源的光转换为图形图案,典型设备是液晶显示器。
1.液晶显示器(LCD):液晶是一类有机化合物,在一定的温度范围内不但有像液体那样的流动性,而且具有像晶体那样的各项异性。
液晶的电光效应:由于液晶具有各项异性以及在外来电场、磁场、应力、温度等作用下容易改变其分子排列的特性,等液晶分子的某种排列状态在电场作用下变为另一种排列状态时,液晶的光学性质随之改变,这种产生光被电场调制的现象称为液晶的电光效应。
液晶显示的机理:液晶显示器就是利用液晶的电光效应,通过施加电压改变液晶的光学特性,从而造成对入射光的调制,使通过液晶的透射光或反射光受所加电压的控制,达到显示的目的。
2.等离子体显示板
等离子体显示器也称气体放电显示器(gas-discharge display),其结构如下图所示。通常用包括氖气在内的混合气体充入两块玻璃板之间的区域,两块玻璃板上分别放置垂直、水平导电带,在成对的水平和垂直导电带上施以点火电压,导致两导电带交叉点处的气体进入辉光放电的电子和离子等离子区,从而显示图形。
3.发光二极管(LED)
图形显示子系统
现在常用的PC图形显示子系统包括哪儿三个结构? 帧缓冲存储器 ,显示控制器 ,ROM BIOS
帧缓冲存储器:存储屏幕上像素的颜色值,简称帧缓冲器,俗称显存。
显示控制器: 主要功能是不断地读取帧缓存中的图像点阵,并转换成RGB三色信号并配备同步信号送至显示器,即可刷新屏幕。
显示处理器: 把CPU从图形显示处理的事务中解脱出来。
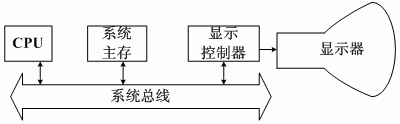
1.早期的光栅图形显示子系统
早期的光栅图形显示子系统如下图所示,帧缓冲存储器可以位于系统主存的任意位置,显示控制器通过系统总线访问帧缓冲存储器,以刷新屏幕。
2.目前常用的光栅图形显示子系统
在目前常用的光栅图形显示子系统中,帧缓冲存储器由显示控制器直接访问,它既可以使用系统内存的固定区域,又可以是专用的显示内存。
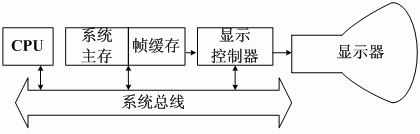
在如上图所示的显示子系统中,显示图形时所需的扫描转换工作直接由CPU来完成,即由CPU计算出表示图形的每个像素的坐标并将其属性值写入相应的帧缓存单元。
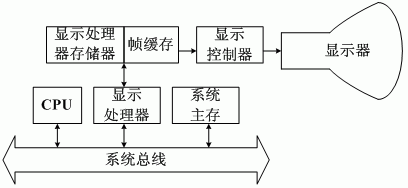
3.发展的光栅图形显示子系统
发展的光栅图形显示子系统的结构如下图所示,除了帧缓存和显示控制器外,还包含显示处理器和独立的显示处理器存储区域。显示处理器,又叫图形控制器或显示协处理器,它的主要任务是扫描转换待显示的图形。
相关概念
1.分辨率
光点是指电子束打在显示器的荧光屏上,显示器能够显示的最小的发光点,一般用其直径来标明光点的大小。
像素点是指图形显示在屏幕上时候,按当前的图形显示分辨率所能提供的最小元素点。像素点可以看作是光点的集合。
图形显示技术中有三种分辨率:
(1)屏幕分辨率(光点数×光点数):也称光栅分辨率或物理分辨率,它决定了显示系统最大可能的分辨率,通常用水平方向上的光点数与垂直方向上的光点数的乘积来表示。
(2)显示分辨率(字符数×字符数):是计算机显示控制器所能够提供的显示模式分辨率,实际应用中简称为显示模式。对于文本显示方式,显示分辨率用水平和垂直方向上所能显示的字符总数的乘积表示;对于图形显示方式,则用水平和垂直方向上所能显示的像素点总数的乘积表示。
(3)图形的存储分辨率(帧缓冲区大小):是指帧缓冲区的大小,一般用缓冲区的字节数表示。由于帧缓冲存储器的大小不仅与显示分辨率有关,还与像素点的颜色数有关。
帧缓存大小的计算为:
其中:x、y分别为表示当前显示分辨率下x、y方向上的像素点总数,n为颜色数或灰度等级数。
2.像素与帧缓存
屏幕上一个像素点就对应帧缓存中的一组信息。对应的方式有以下两种:
(1) 组合像素法(Packed Pixel Method)
在组合像素法中,一个图形像素点的全部信息被编码成一个数据字节,按照一定方式存储到帧缓存中,编码字节的长度与点的属性(如颜色、灰度)有关。
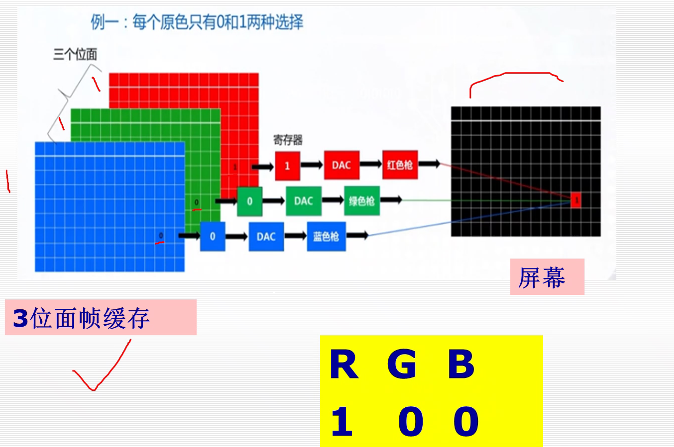
(2)颜色位面法(Color Plane Method)
在颜色位面法中,帧缓存被分成若干独立的存储区域,每一个区域称为一个位面(BitPlane),如下图所示,每个位面控制一种颜色或者灰度,每一个图形像素点在每个位面中占一位,通过几个位面中的同一位组合成一个像素。
3位面帧缓存的容量计算:8种颜色
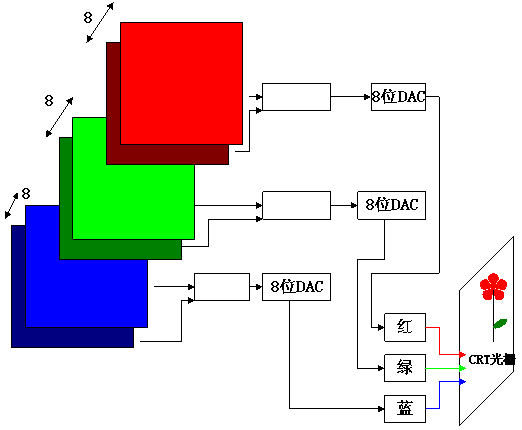
24位面帧缓存:
3.颜色查找表(Color Lookup Data)
颜色查找表也称调色板,是由高速的随机存储器组成,用来储存表达像素色彩的代码。此时帧缓冲存储器中每一像素对应单元的代码不再代表该像素的色彩值,而是作为查色表的地址索引,如下图所示的具有24位面彩色帧缓存和10位颜色查找表的光栅显示器。
采用颜色查找表后可以提高总的光强等级,即总的颜色数,但每屏可显示的颜色数还是受帧缓存中单个像素点所占用的位数决定。
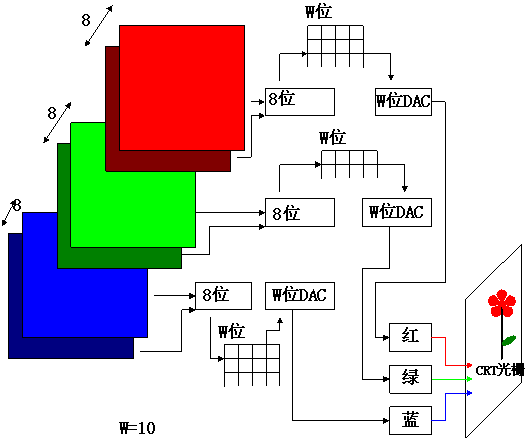
比如原来有2^24种颜色,加上颜色查找表后,可以达到 2^30种颜色
4.显示长宽比
显示长宽比,即水平点数与垂直点数之比。当屏幕显像管的长宽比等于4:3,为了使屏幕两个方向上相同像素点数产生同样长度的线段,以使图形不至发生畸变,水平方向上的像素点数与垂直方向上的像素点数之比大约也是4:3。
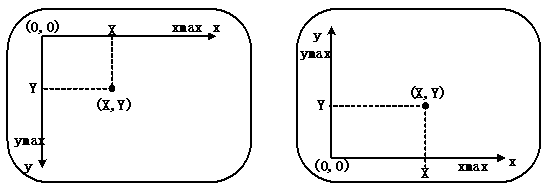
5.屏幕坐标系
常用的屏幕坐标系有如下图所示的两种。
第四章:图形的表示与数据结构
1.图素和体素
在二维图形系统中将基本图形元素称为图素或图元,而在三维图形系统中称为体素。
图素是指可以用一定的几何参数和属性参数描述的最基本的图形输出元素,包括点、线、圆、圆弧、椭圆、二次曲线等。体素的定义相对复杂一些,是三维空间中可以用有限个尺寸参数定位和定形的体。
2.刚体运动和拓扑运动
刚体运动:不该百年图形上任意两点间的距离,也不改变图形的几何性质的运动。
拓扑运动:允许形体做弹性运动,即在拓扑关系中,对图形可随意地伸张扭曲。但不允许把不同的点合并成一个点。
3.坐标系
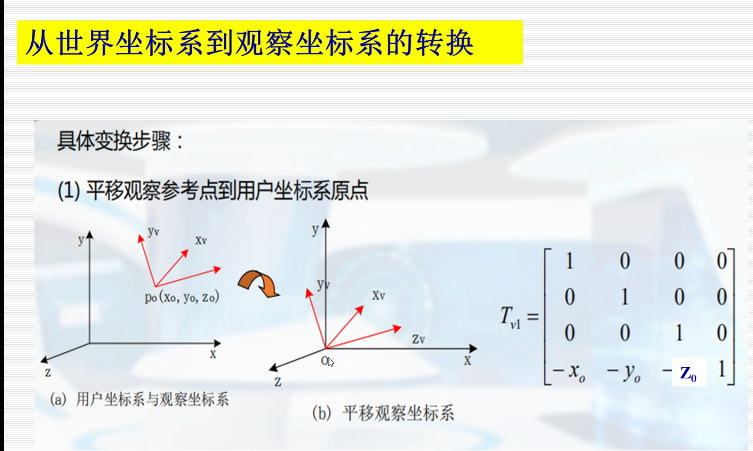
建模坐标系,用户坐标系,观察坐标系,规格化设备坐标系,设备坐标系
4.欧拉公式
对于简单多面体来说:V-E+F=2 顶点数-边数+面数=2
若不满足欧拉公式肯定不是有效形体,若满足欧拉公式也不一定是有效形体。
5.数据结构
三维形体的信息:几何信息,拓扑信息,属性信息
几何信息的数据结构: 比如定点表,面表,边表
拓扑信息的数据结构:比如 边表扩充成包括指向面表和顶点表的指针。
属性信息:物体透明度,反射度,纹理 等。
三维形体的表示
分为线框模型和实体模型。
线框模型
线框模型存在着几个缺陷。
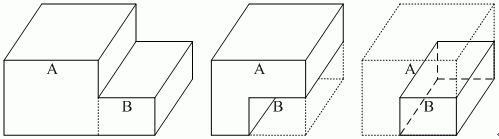
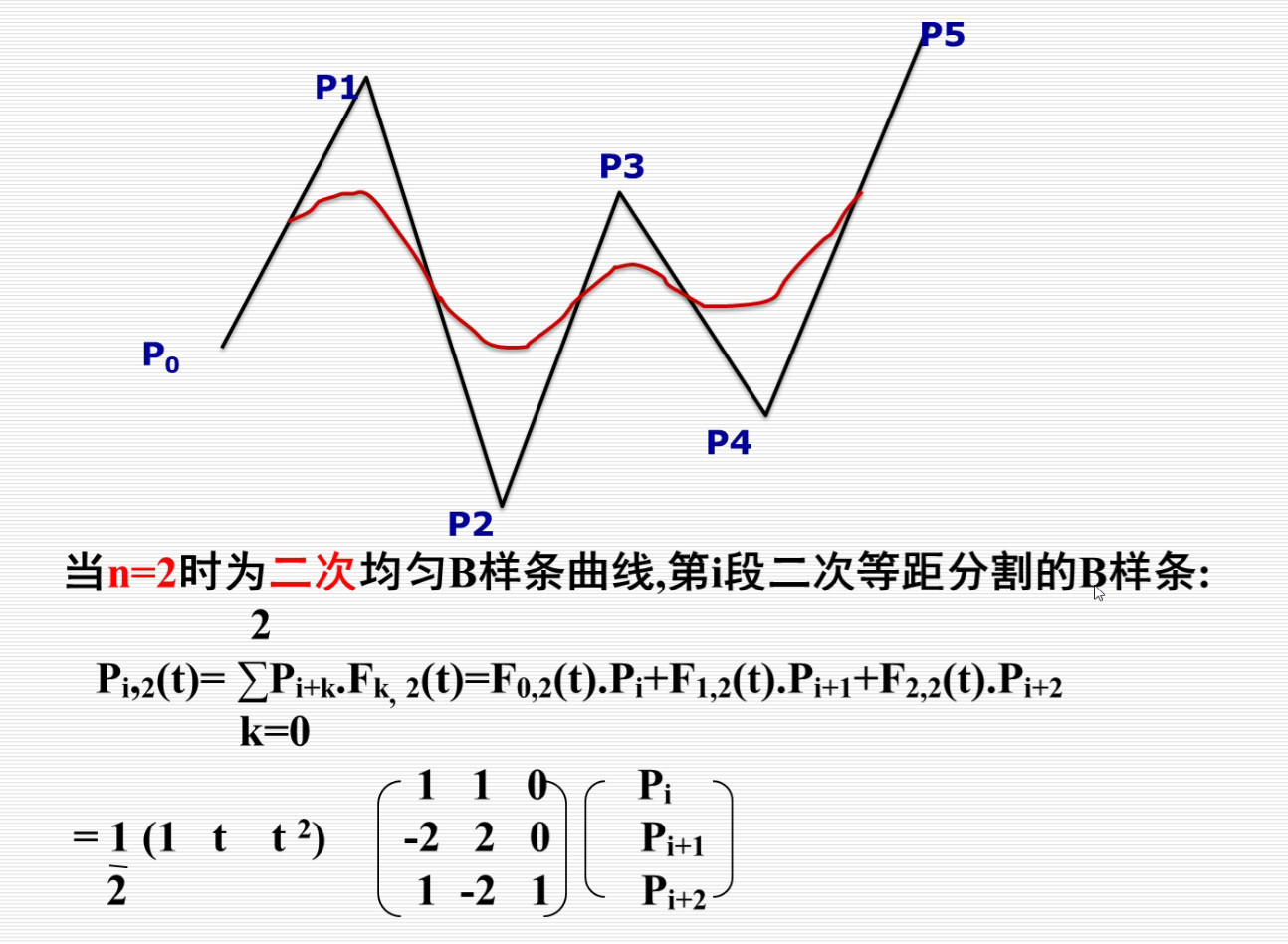
(1)用三维线框模型表示三维形体常具有二义性,如下图所示的图形可以有多种理解方式。
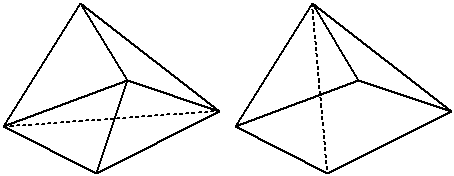
图4-12 线框模型的二义性
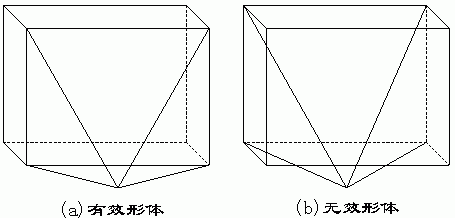
(2)由于不存在面的信息,三维线框容易构造出无效形体,如下图所示。
(3)由于不能表示出曲面的轮廓线,所以不能正确表示曲面信息。
(4)无法进行图形的线面消隐。
(5)生成复杂形体时,线框模型要求输入大量的数据,加重用户的输入负担。
(6)难以保证数据的统一性和有效性。
实体模型:多边形表面模型
1.多边形表
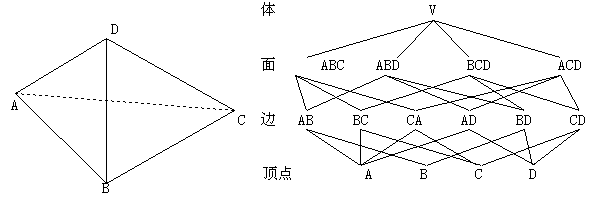
数据结构: 几何信息:定点表,边表,面表这一类的表。
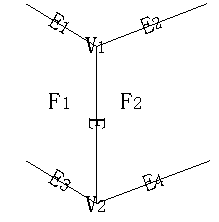
拓扑信息:如将边表扩充成包括指向面表和顶点表的指针,由此可构造出如下图所示的翼边结构 表示(Winged Edges Structure)。
属性信息:颜色,纹理,质感
2.平面方程:
可以利用平面方程:
(1)求得平面的法向量。
(2)鉴别空间上的点与物体平面的位置关系。
(3)判别点在面的内部或外部。
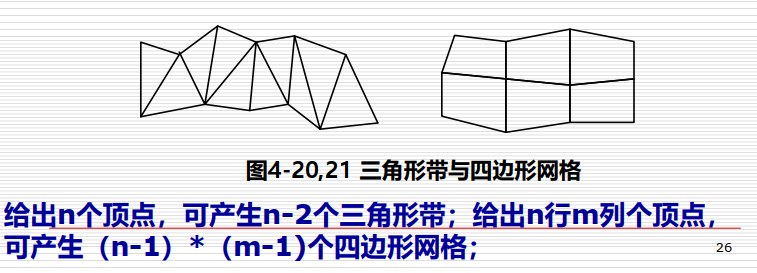
- 多边形网格(polygon mesh)
三维形体的曲面边界通常用多边形网格(polygon mesh)的拼接来模拟。常用的是如下图所示的三角形带和四边形网格。
实体模型:扫描表示法
扫描表示法(sweep representation)可以利用简单的运动规则生成有效实体。扫描表示包含两个要素:作扫描运动的基本图形以及扫描运动的方式。
常见扫描运动的方式有:
(1)旋转扫描:沿图形路径从0到360度的角度范围内移动。
(2)非圆形路径扫描:给定描述路径的曲线函数和沿路径移动的距离。
(3)广义扫描法:沿扫描路径变化剖面的形状和大小,或者当移动该形状通过某空间区间时,可以变化剖面相对于扫描路径的方向。
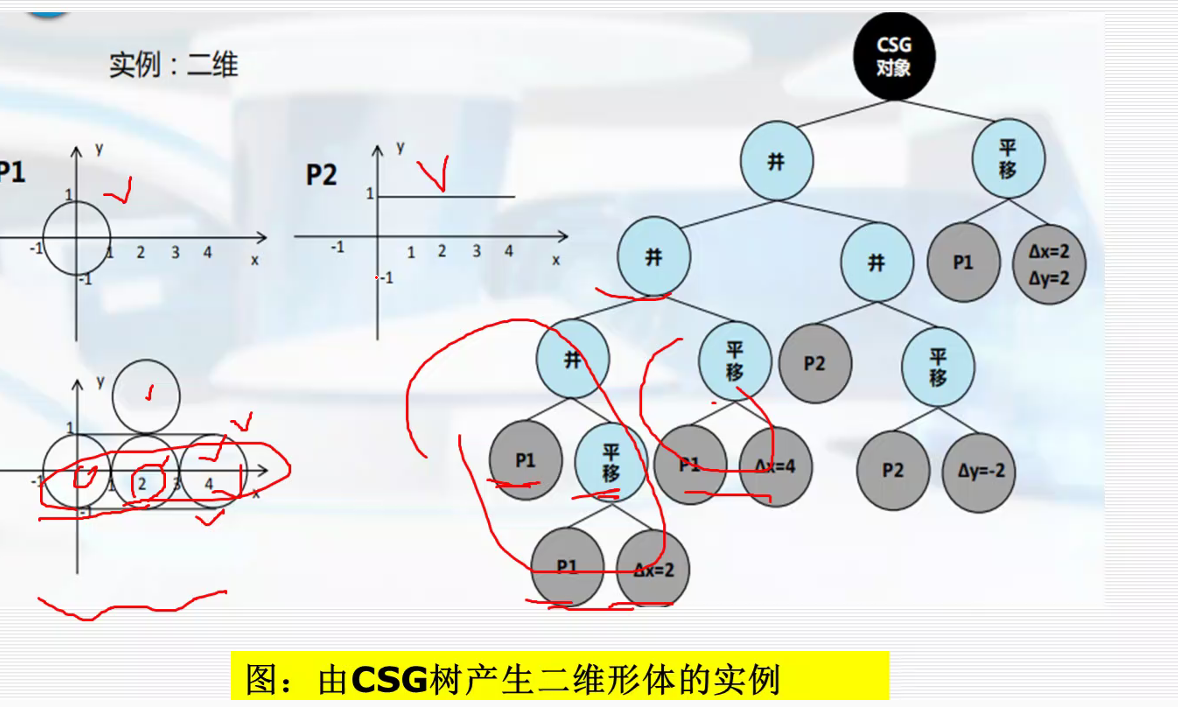
实体模型:构造实体几何法
构造实体几何法(CSG,Constructive Solid Geometry)由两个实体间的并、交或差操作生成新的实体。
GSG树:
实体模型:空间位置枚举表示法
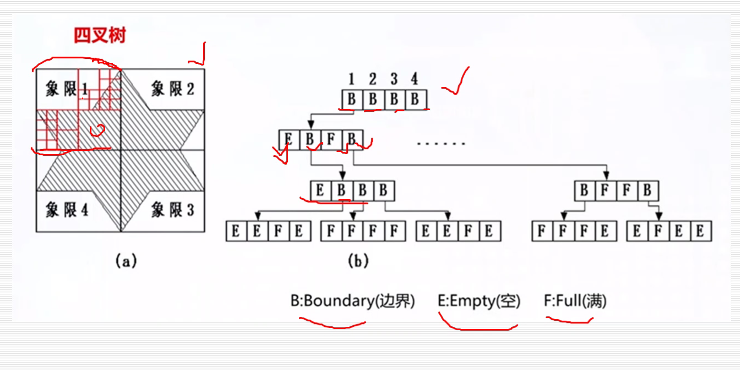
八叉树(octrees)又称为分层树结构,它对空间进行自适应划分,采用具有层次结构的八叉树来表示实体。
1.四叉树: 看准象限的位置,这个和一般坐标系不太一样,总左上开始第一象限,顺时针旋转。
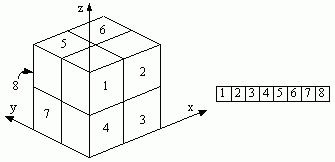
2.八叉树
八叉树方法与四叉树类似,用一个空间的长方体来包围一个三维实体,每次把它分为8个卦限来进行判断。
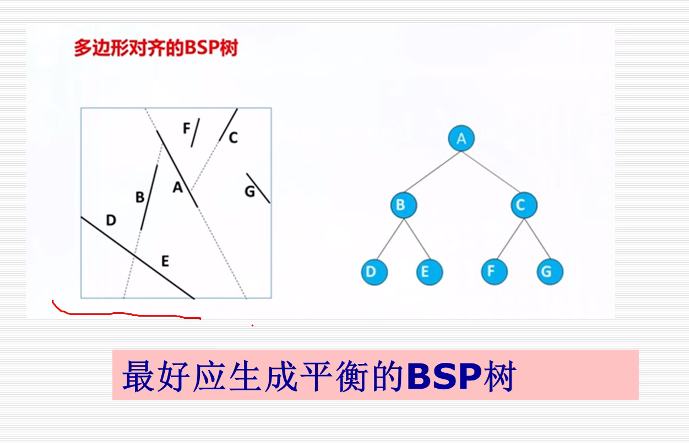
二叉空间分割树(binary space partitioning,BSP)方法每次将一实体用任一位置和任一方向的平面分为二部分。这种方法可将分割平面的位置和方向按适合于实体的空间属性来确定,更为有效。
如何绘制BSP树? https://blog.csdn.net/pleasecallmewhy/article/details/8426183
下图为面的俯视图,A面两边为B,C. B的两面为D和E。 C的两面为F和G
非规则对象的表示
基于分数维理论的随机模型:由A.Fournier等人基于分数维理论提出来的一种过程式模拟,它能够有效地模拟海岸线和山脉等自然景物。
基于文法的模型: 由A.R.Smith用正规文法来构造植物等结构性较强的自然景物,是一个并行重写系统,由一组产生式规则组成。
粒子系统模型:由随着时间变化的一组粒子组成的,此模型可以用来模拟火、烟、雾等,也可以用来模拟被风吹动的草和灌木等。
第五章:基本图形生成算法
直线的扫描转换
直线的绘制要求:
(1)直线要直;
(2)直线的端点要准确;
(3)亮度、色泽均匀;
(4)画线速度快;
(5)具有不同的色泽、亮度、线型等。
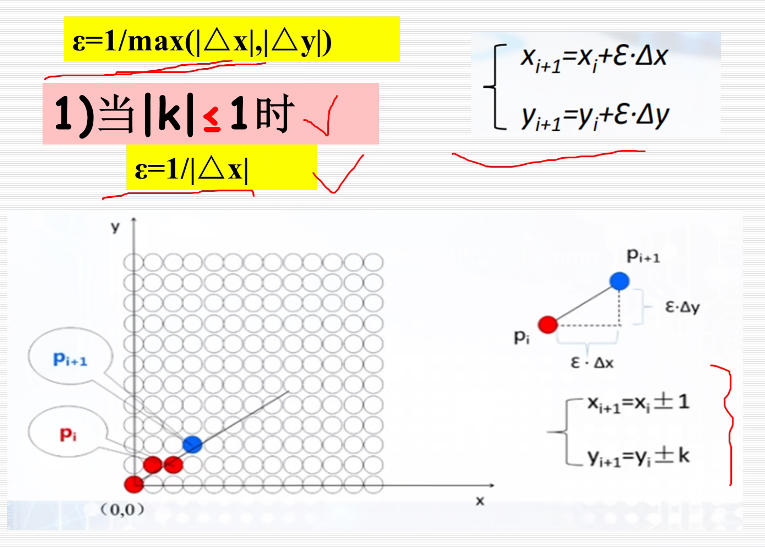
1.数值微分法(DDA)
数值微分法(DDA法,Digital Differential Analyzer)是一种直接从直线的微分方程生成直线的方法。给定直线的两端点P0(x0, y0)和P1(x1, y1),得到直线的微分方程如下:
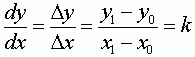
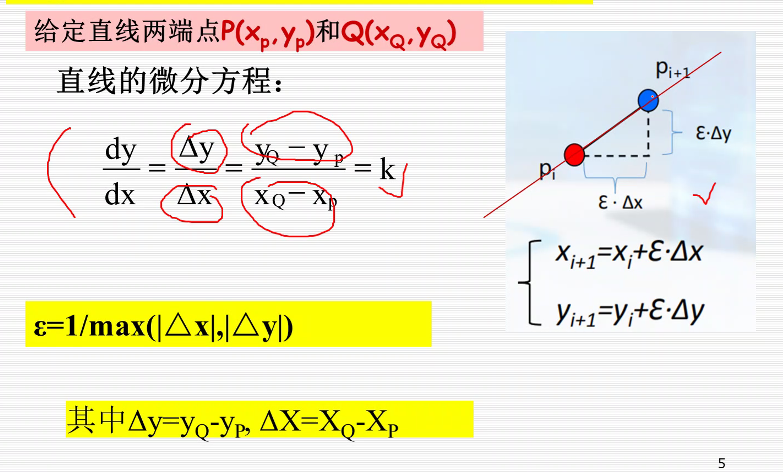
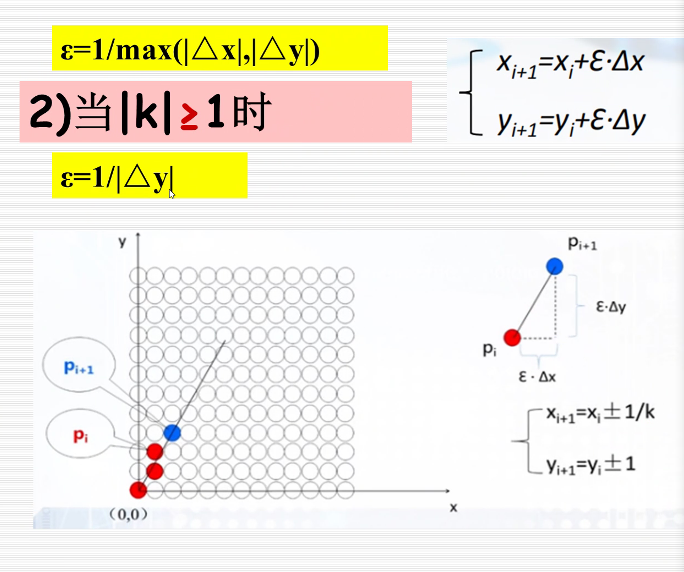
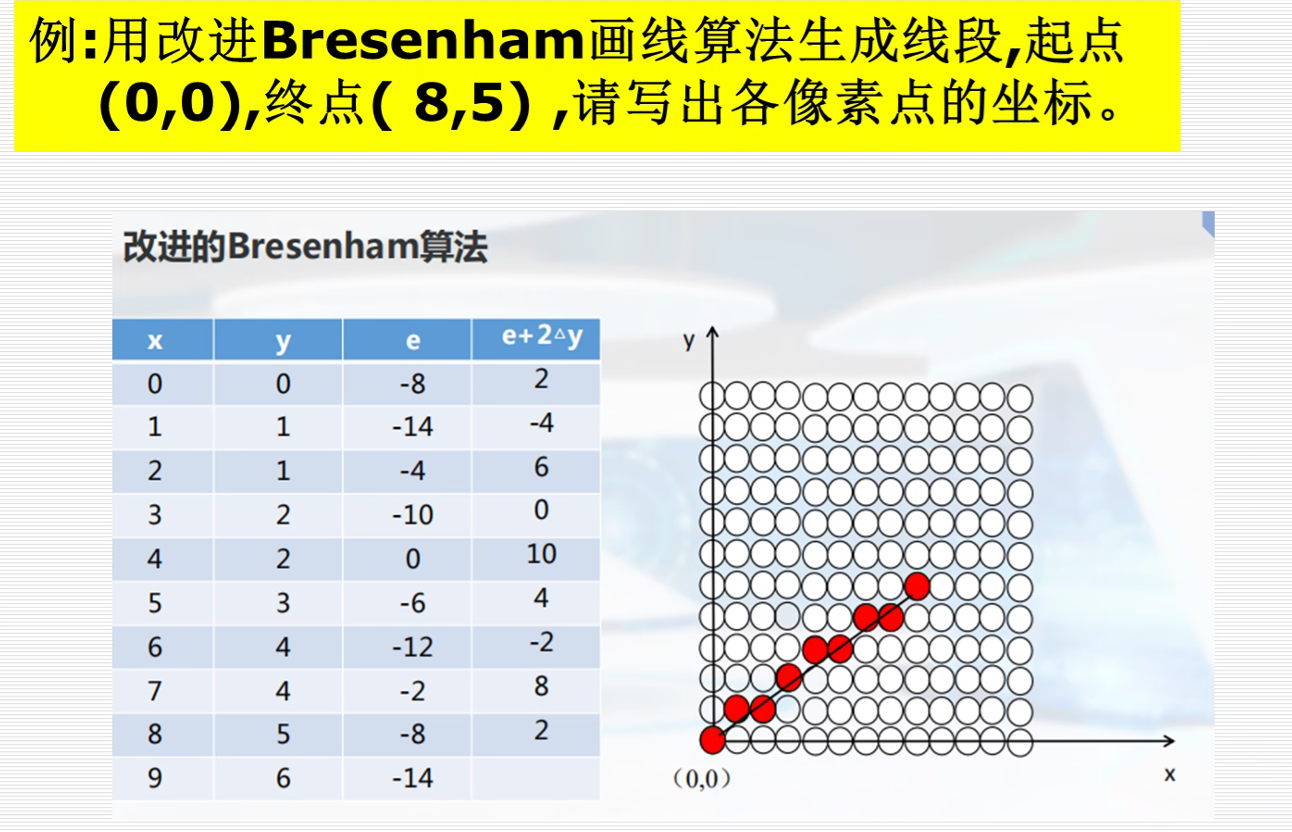
求出来可能是小数,然后要四舍五入取整。

(上图黄色框中漏了一个(2,1)!!!)
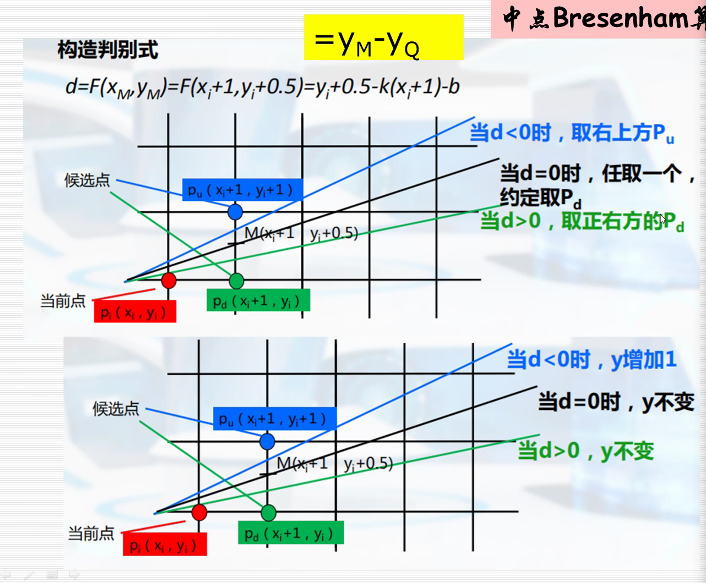
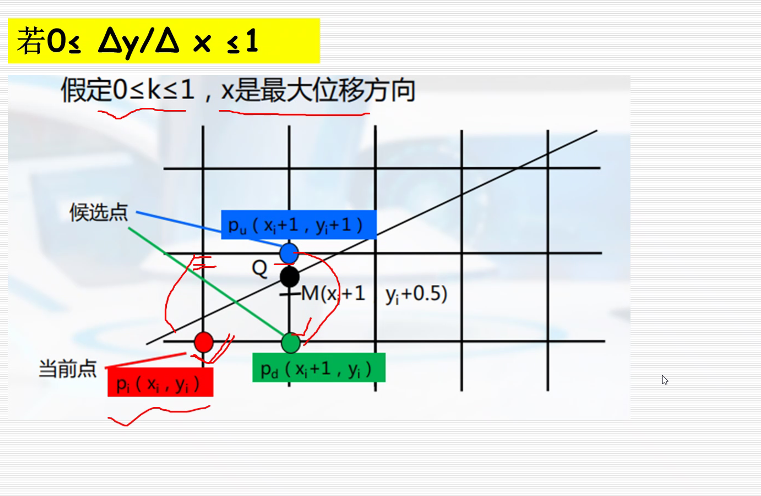
2.中点Bresenham算法
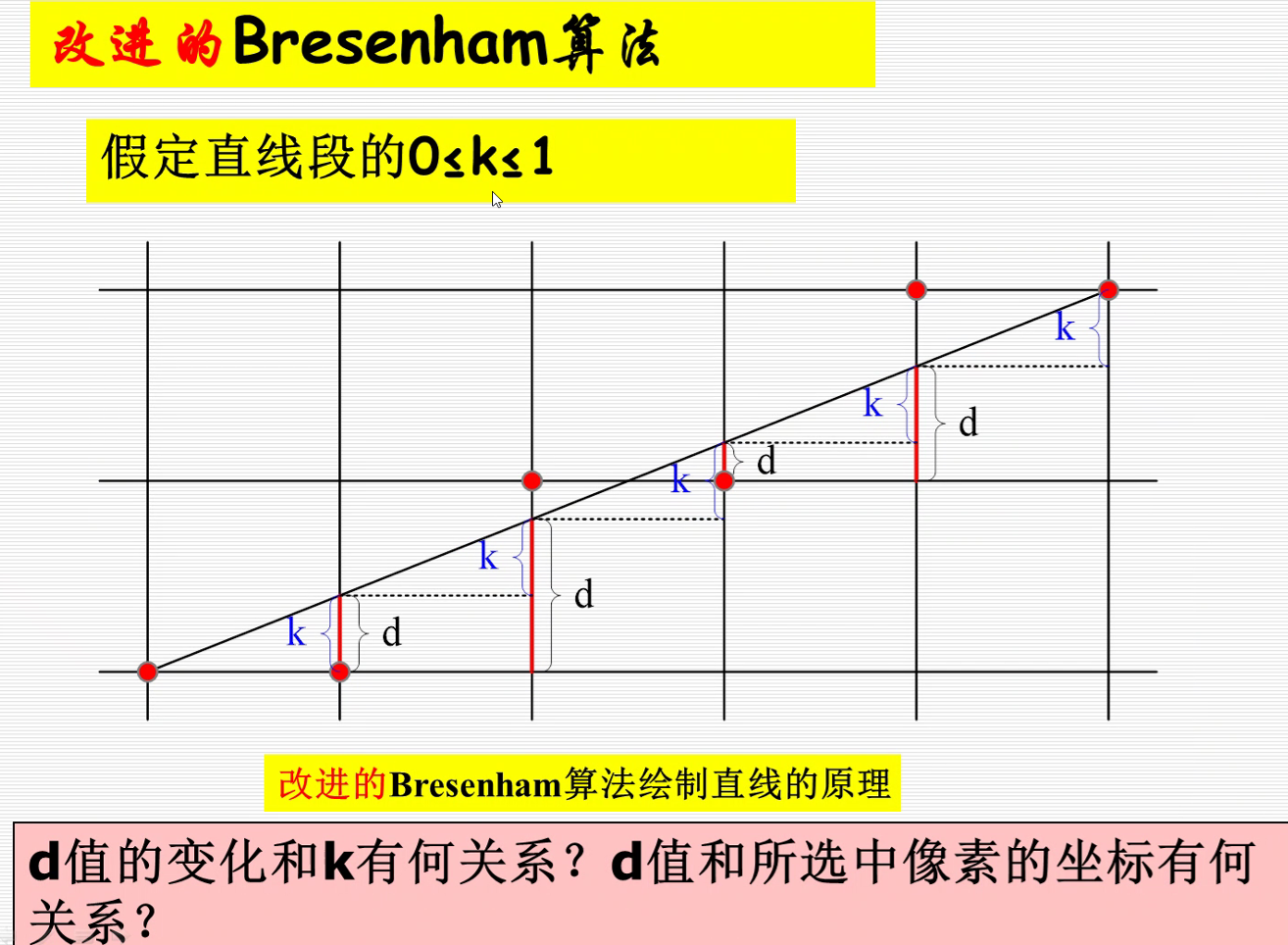
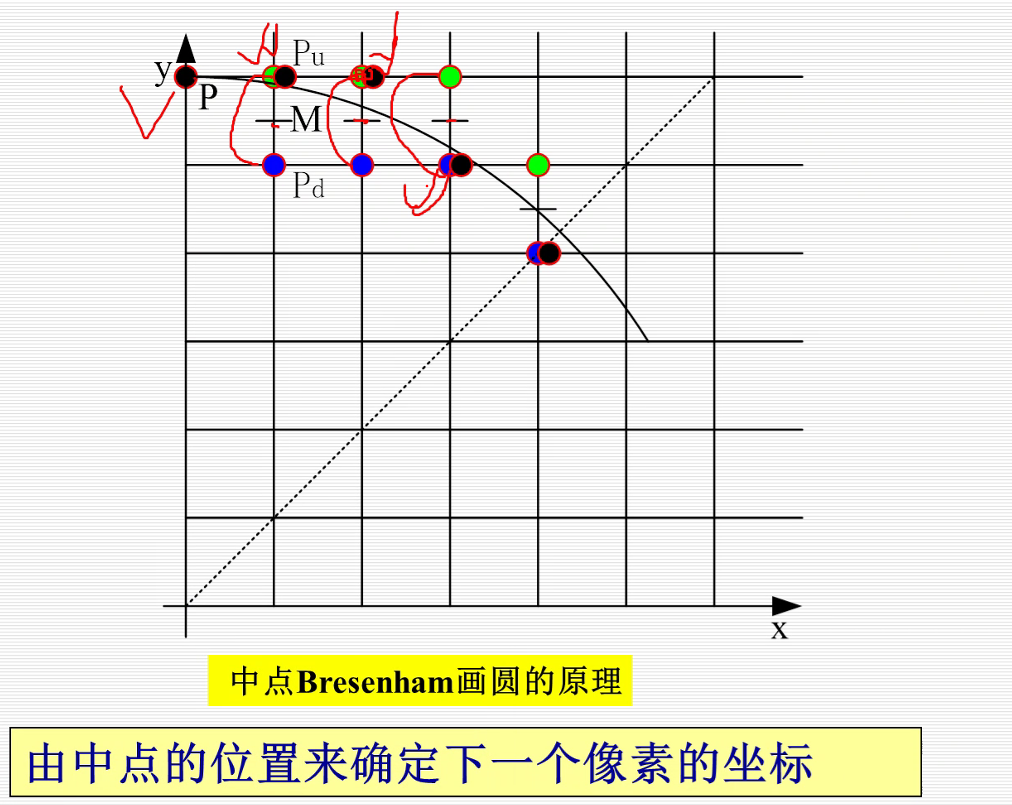
在增量大的方向变化一个步长,从当前点(红色)考虑变化大方向的下两个点(蓝色,绿色点),然后看蓝色和绿色哪个点和直线距离最近下一个点就选谁(图中选择蓝色点)。
然后把蓝色点看成p~i~接着去找p~u~, p~d~ .
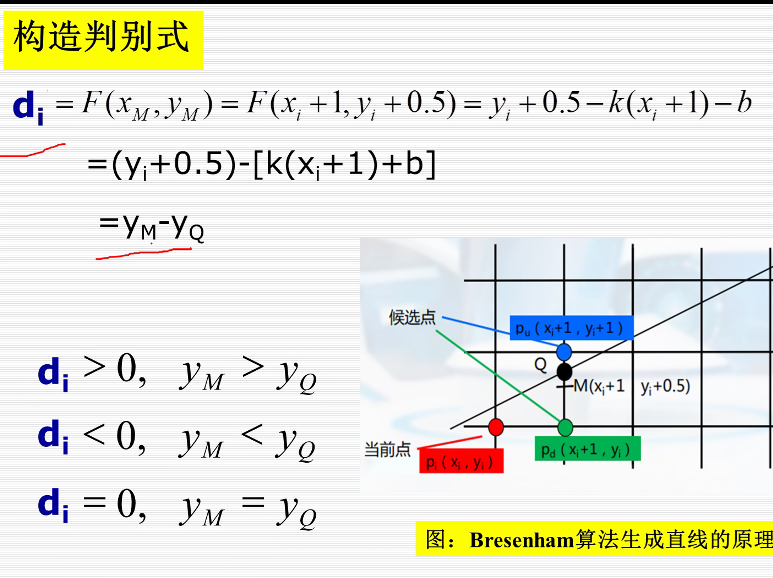
计算递推式(加快运行效率)

进一步增加运行效率(去掉k中的除法)


3.改进的Bresenham算法



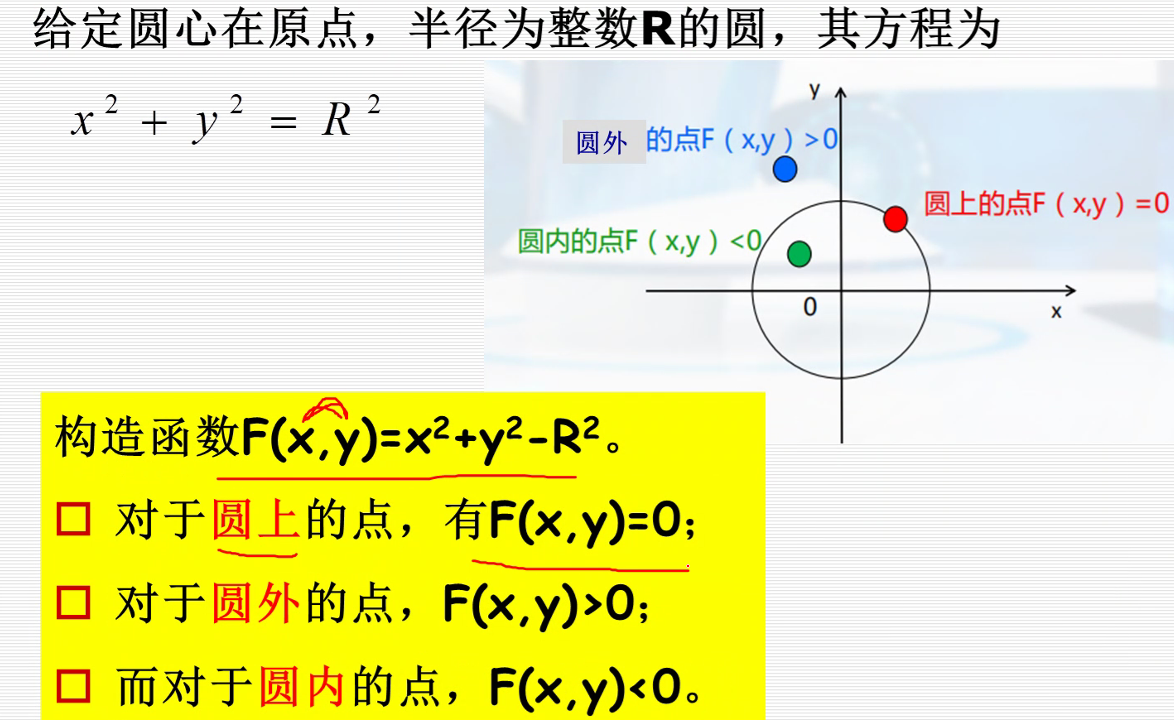
圆的扫描转换
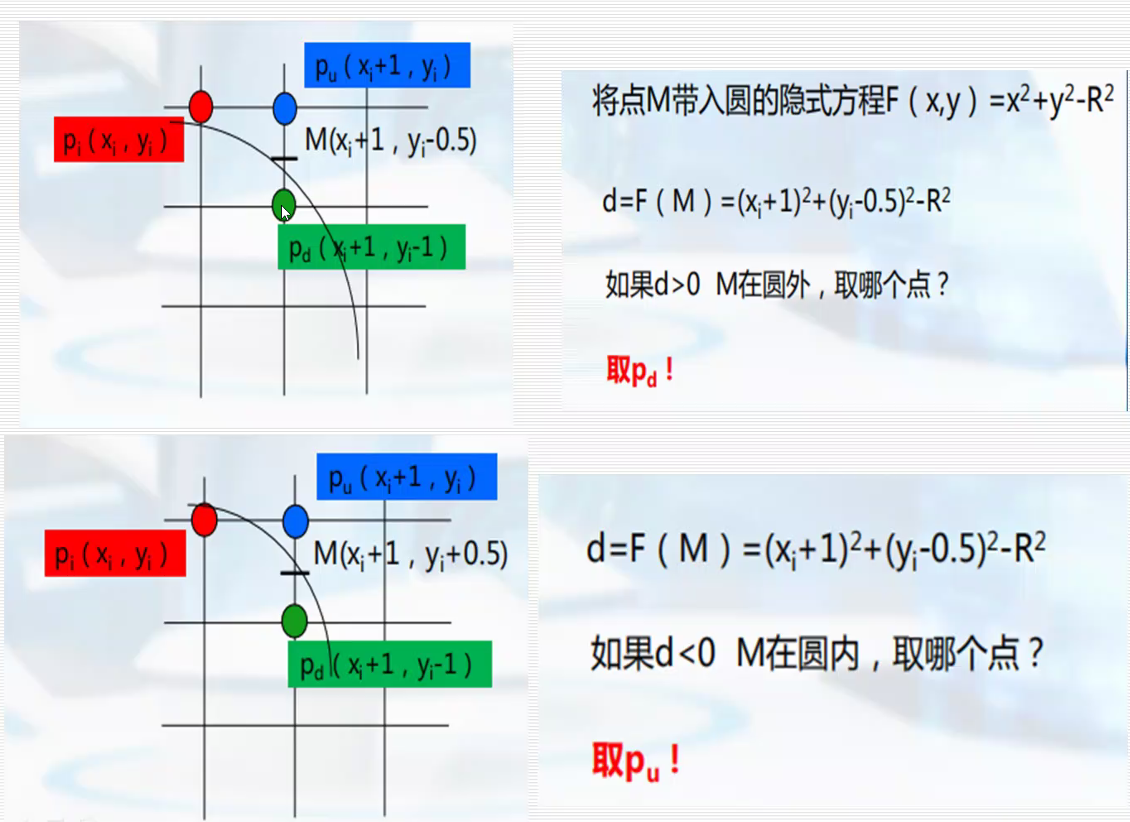
1.中点bresenham画圆算法
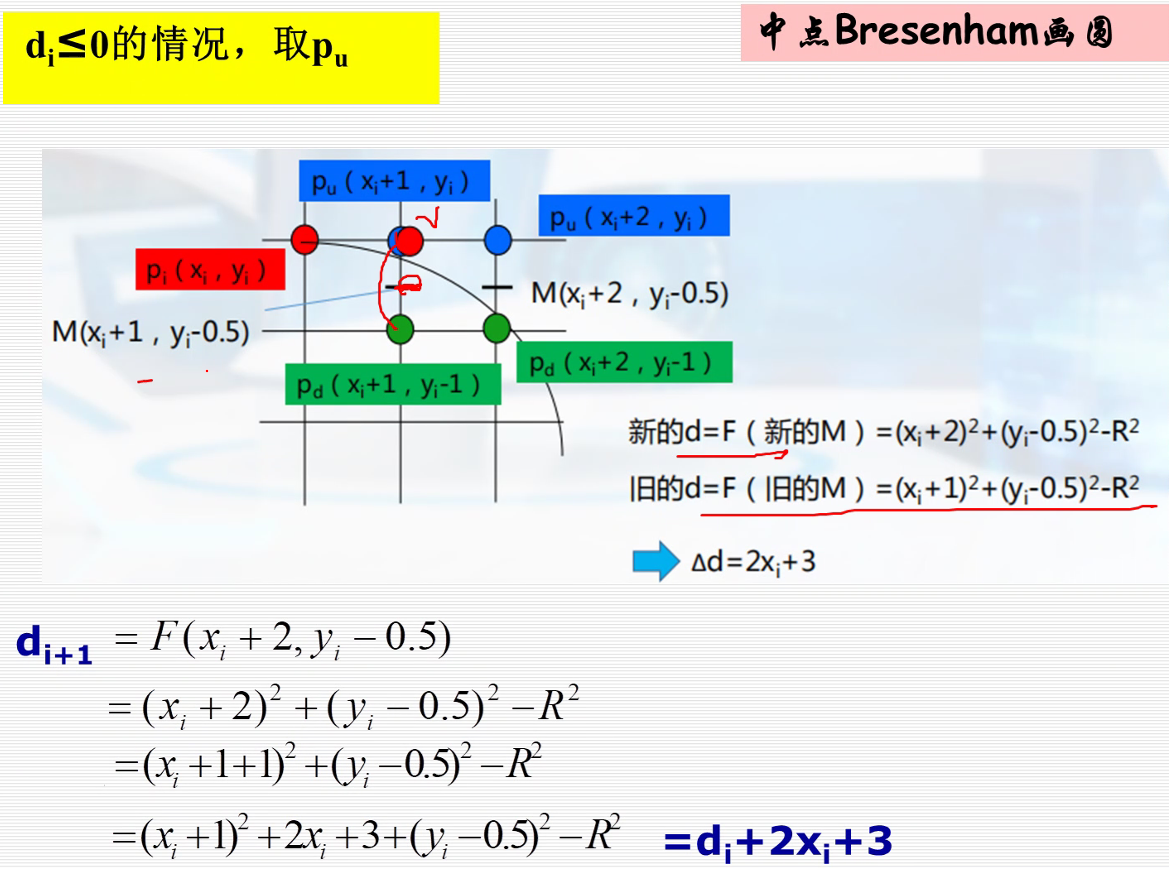
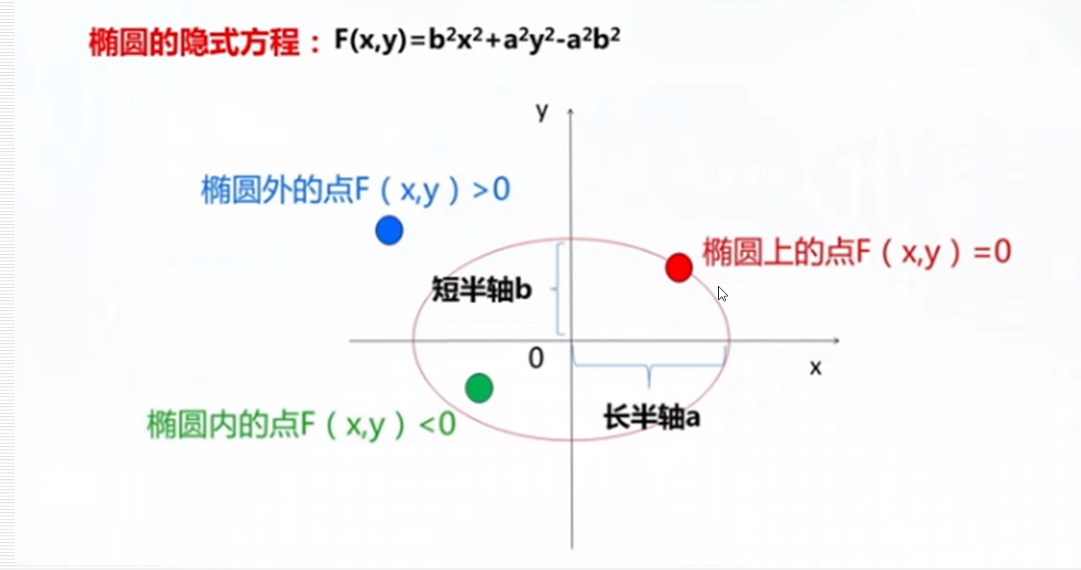
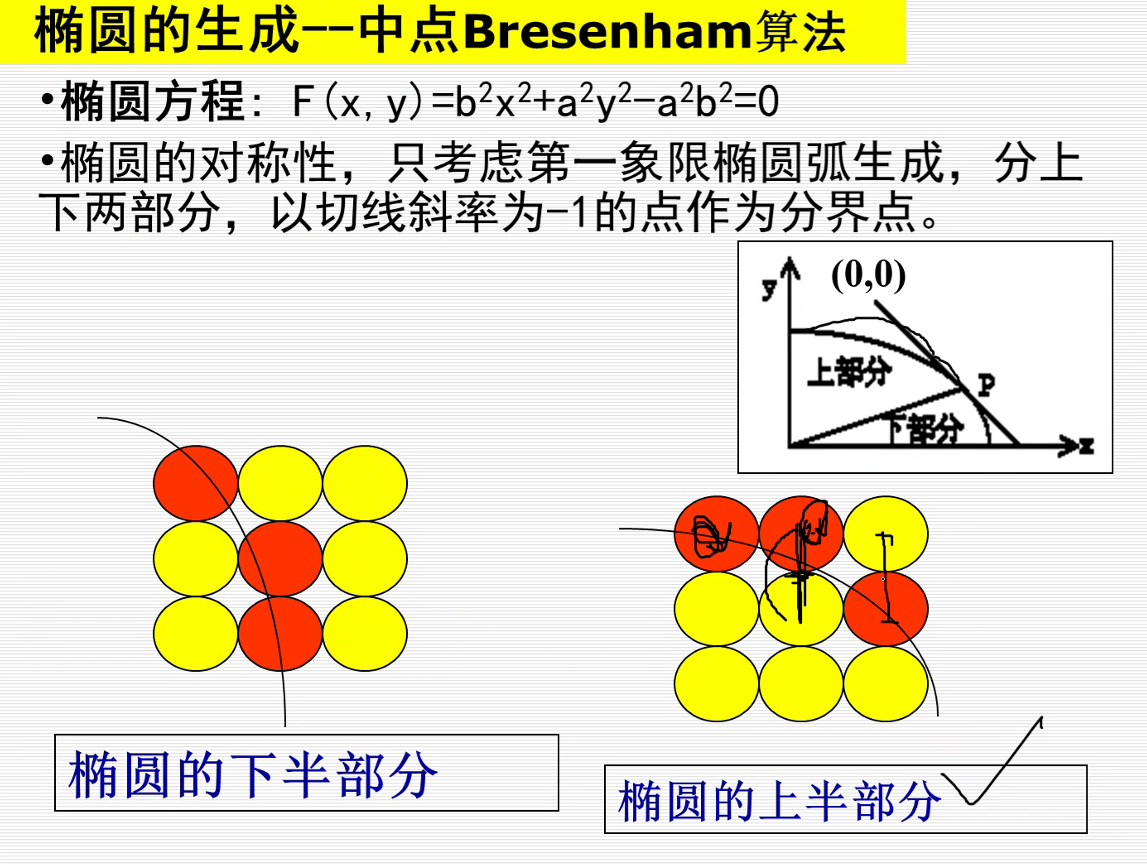
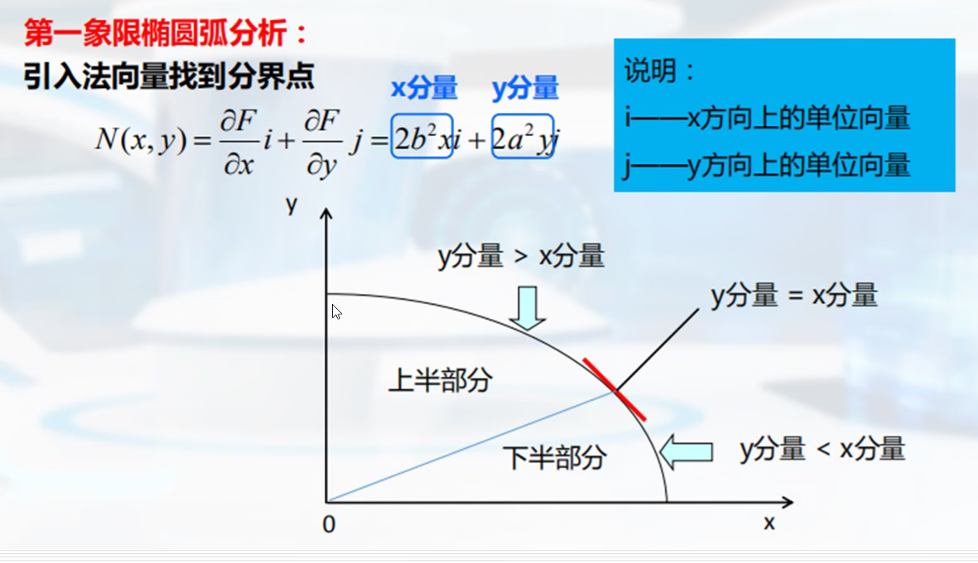
椭圆的扫描转换
中点bresenham算法
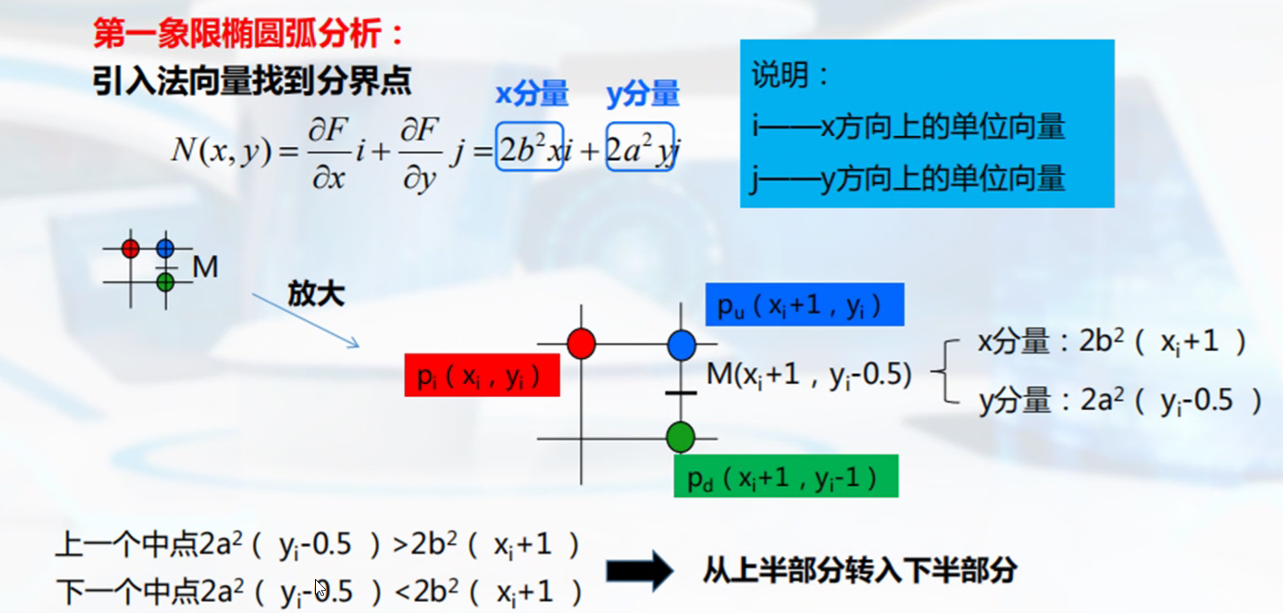
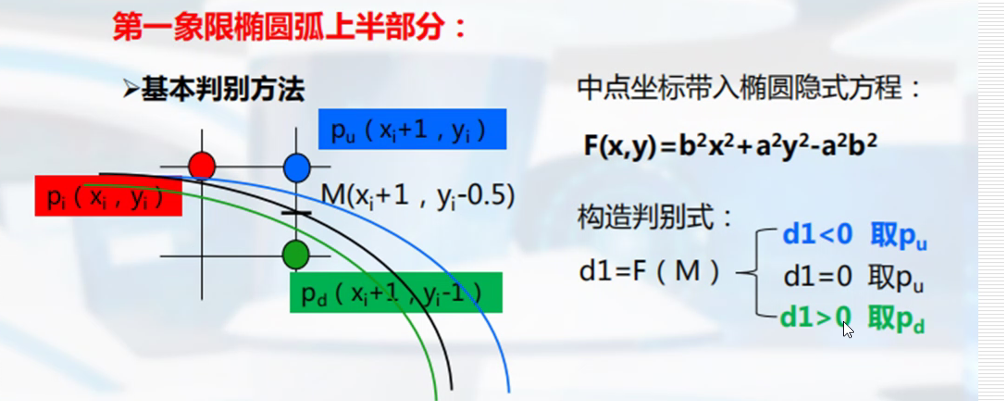
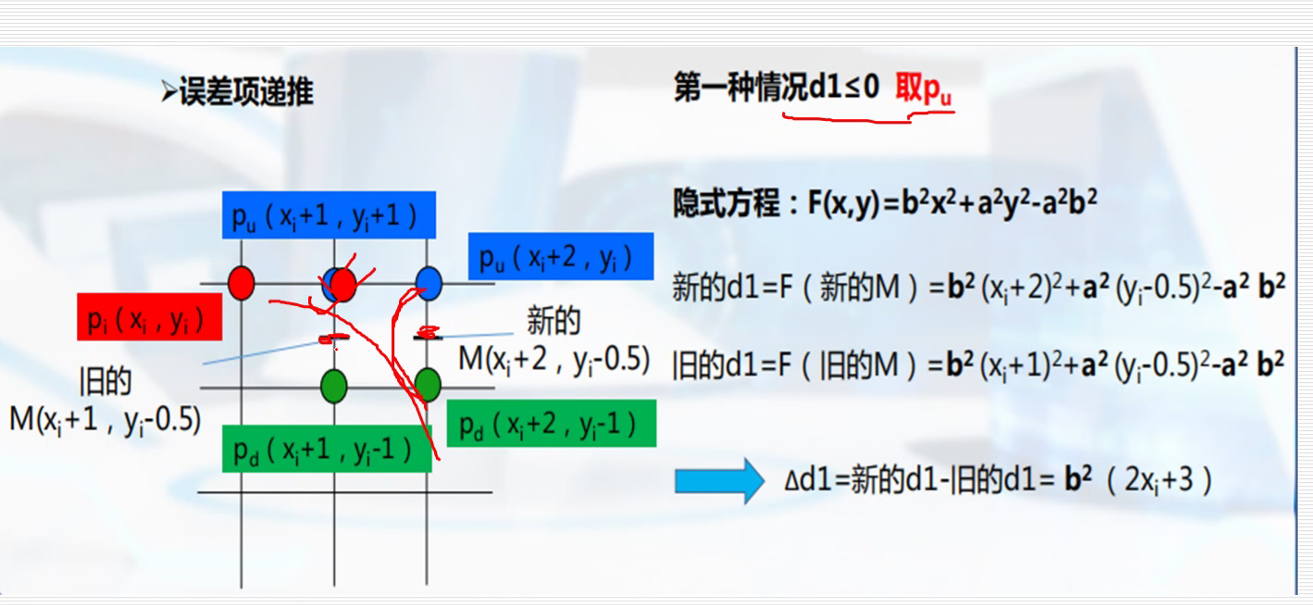
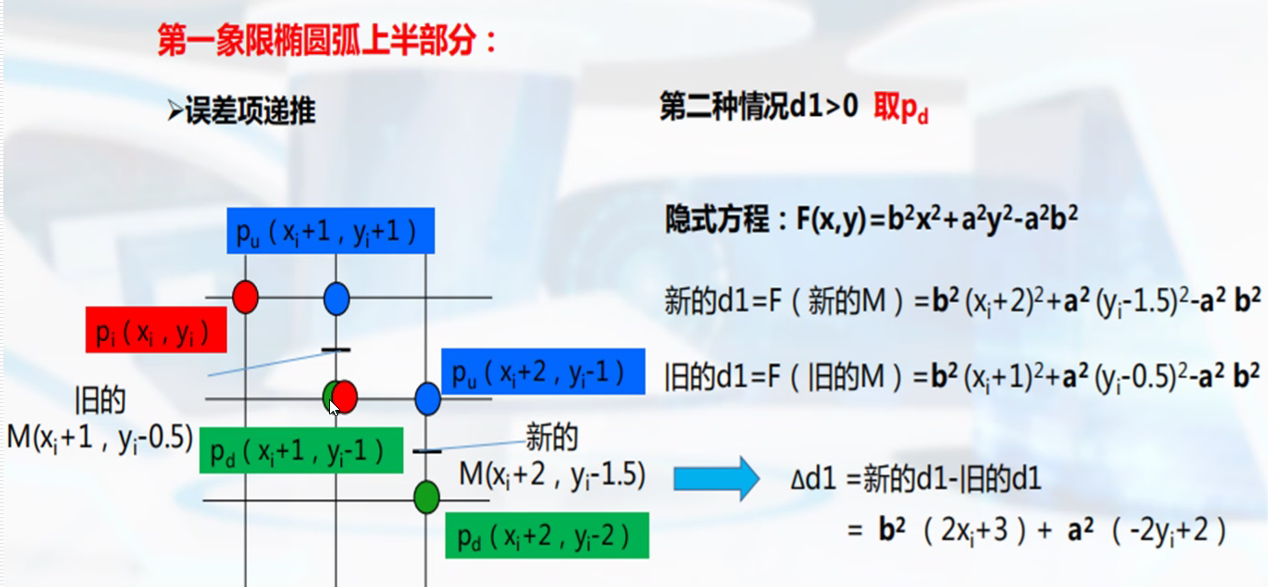
多边形的扫描转换与区域填充
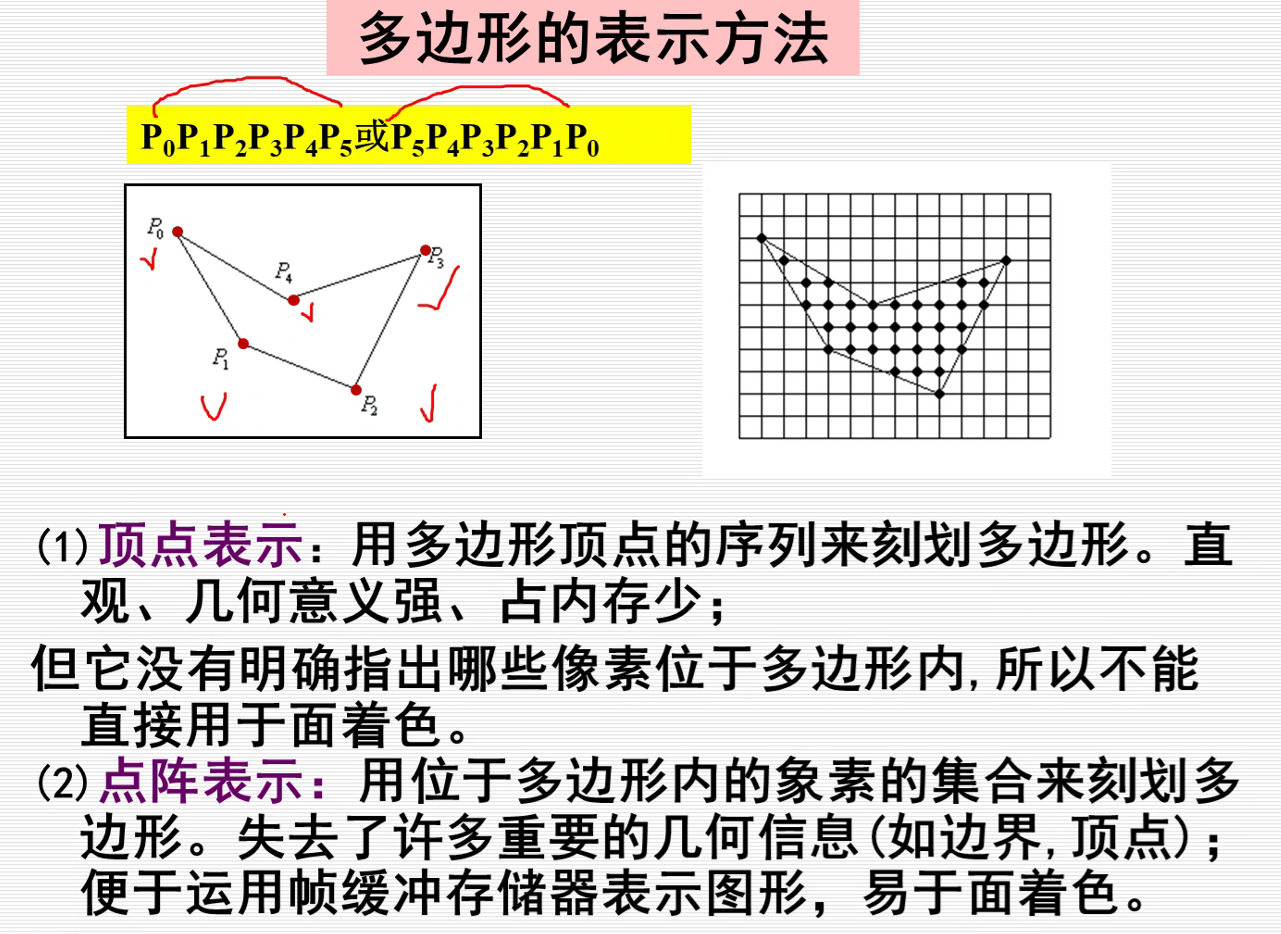
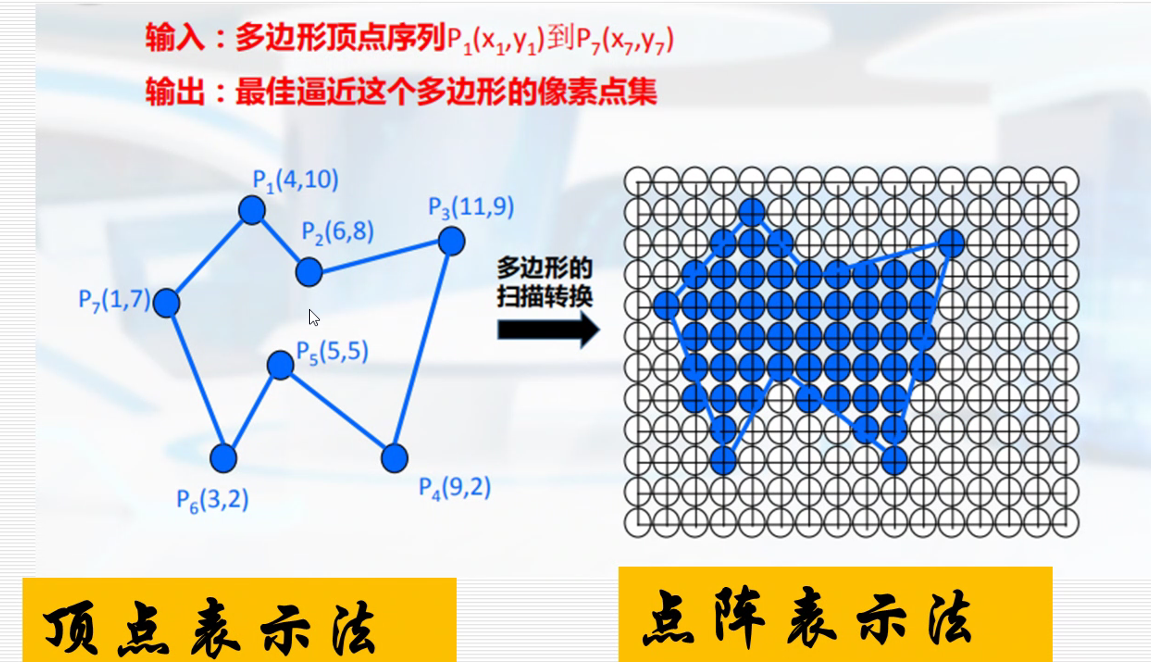
1.X-扫描线算法

基本思想:如下图所示,按扫描线顺序,计算扫描线与多边形的相交区间,再用要求的颜色显示这些区间的所有像素。
算法步骤:
(1)确定多边形所占有的最大扫描线数,得到多边形顶点的最小和最大y值(ymin和ymax)。
(2)从y=ymin到y=ymax,每次用一条扫描线进行填充。填充过程可分为四个步骤:
a.求交:计算扫描线与多边形各边的交点;
b.排序:把所有交点按照递增顺序进行排序;
c.交点配对:交点两两配对,表示扫描线与多边形的一个相交区间;
d.区间填色:将相交区间内的像素置成不同于背景色的填充色。
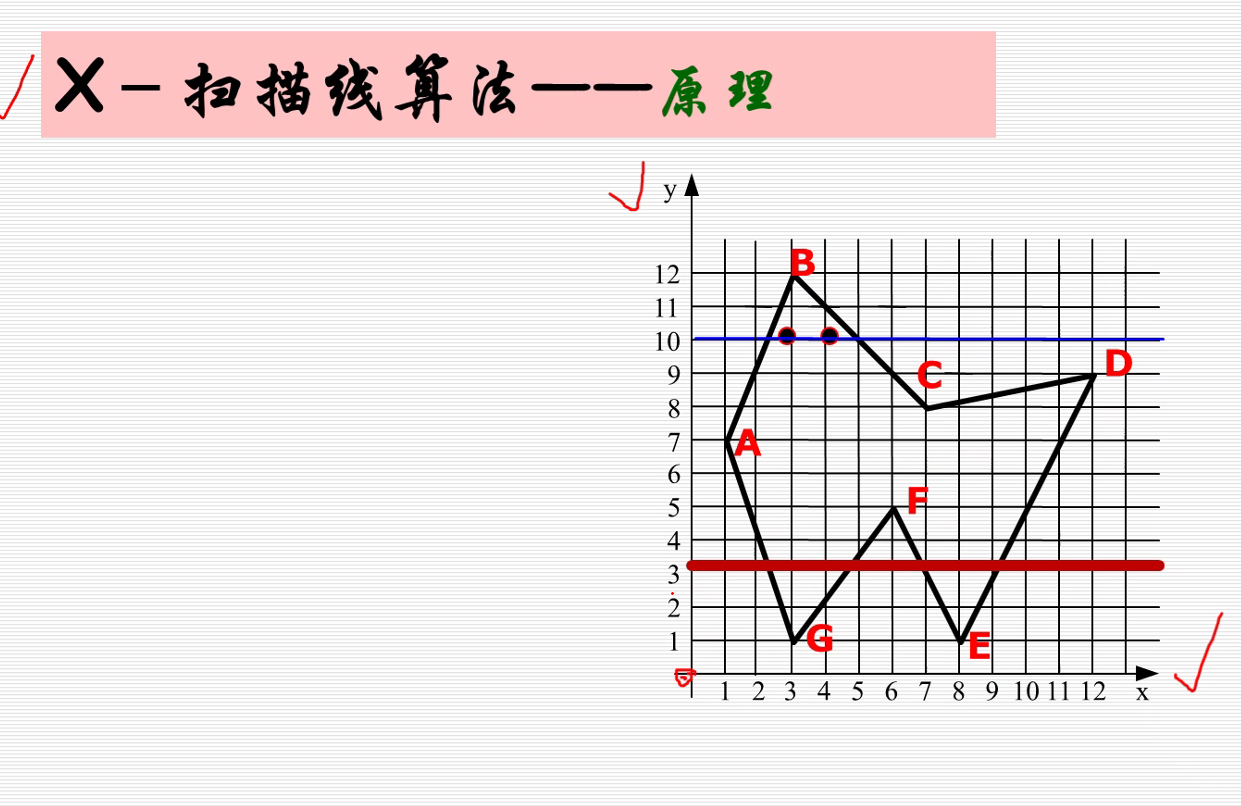
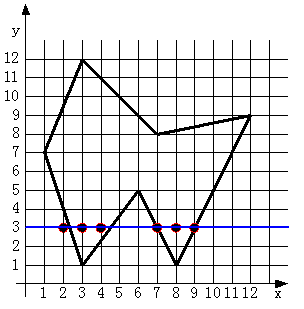
存在问题:当扫描线与多边形顶点相交时,交点的取舍问题。如下图所示,在扫描线y=1,y=5和y=7时,扫描线过多边形的顶点,若不加以处理,交点配对时会发生错误。
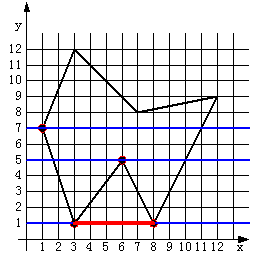
解决方法:当扫描线与多边形的顶点相交时,若共享顶点的两条边分别落在扫描线的两边,交点只算一个;若共享顶点的两条边在扫描线的同一边,这时交点作为零个或两个。实际处理时,只要检查顶点的两条边的另外两个端点的Y值,两个Y值中大于交点Y值的个数是0,1,2,来决定取0,1,2个交点
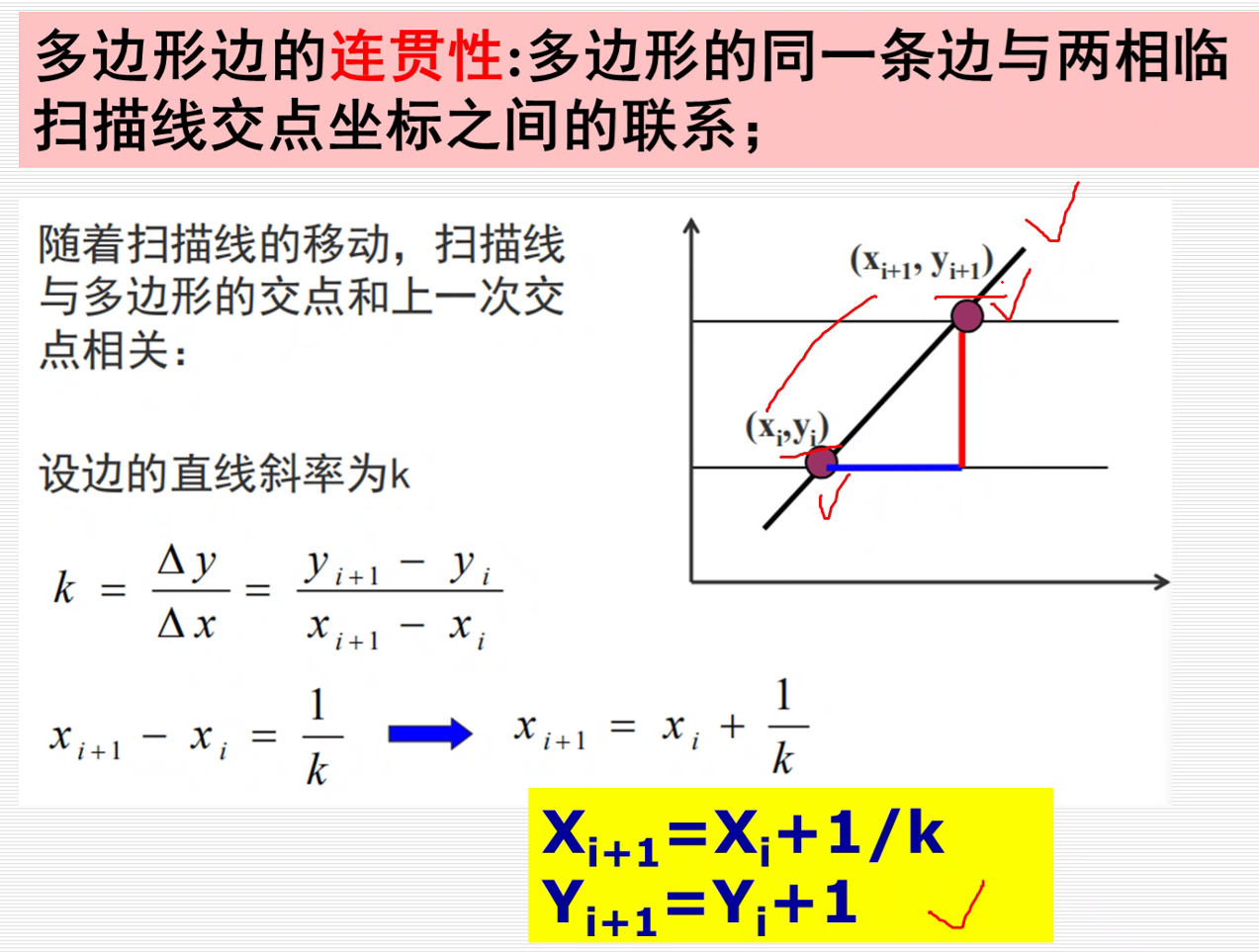
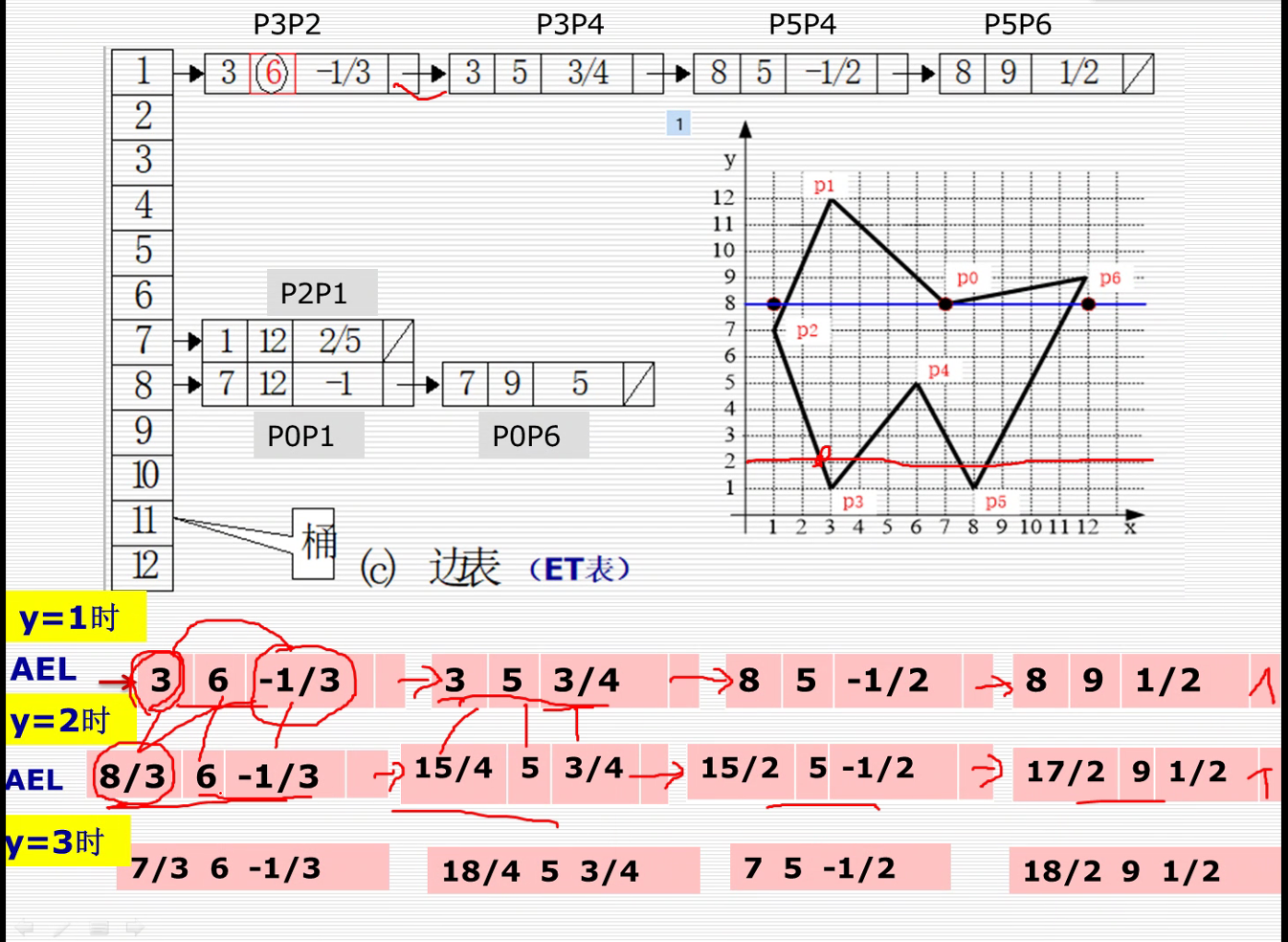
2.改进的有效边算法(y的连贯性算法)
由于x-扫描线算法在处理每条扫描线时,需要与多边形所有的边求交,效率很低,因此需要加以改进,形成改进的有效边表算法。
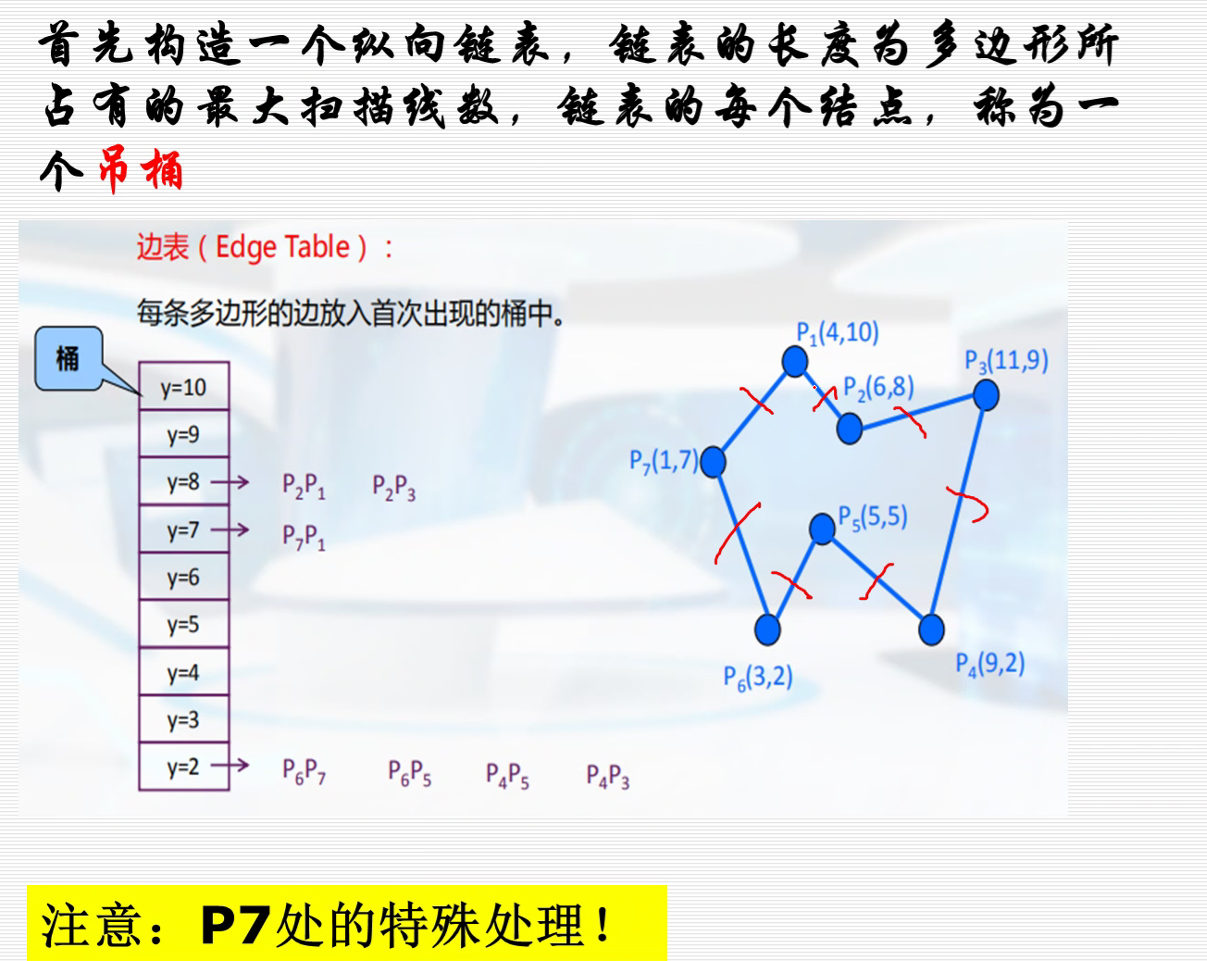
边表:为了方便有效边表的建立与更新,需要构造一个边表(Edge Table)。
(1)首先构造一个纵向链表,链表的长度为多边形所占有的最大扫描线数,链表的每个结点,称为一个桶,则对应多边形覆盖的每一条扫描线。
(2)将每条边的信息链入与该边最小y坐标(ymin)相对应的桶处。也就是说,若某边的较低端点为ymin,则该边就放在相应的扫描线桶中。
(3)每条边的数据形成一个结点,内容包括:该扫描线与该边的初始交点x(即较低端点的x值),1/k,以及该边的最大y值ymax。
x|ymin ymax 1/k NEXT
(4)同一桶中若干条边按X|ymin由小到大排序,若x|ymin 相等,则按照1/k由小到大排序。
为了解决顶点交点计为1时的情形,可将多边形的某些边缩短以分离那些应计为1个交点的顶点,如下图所示。
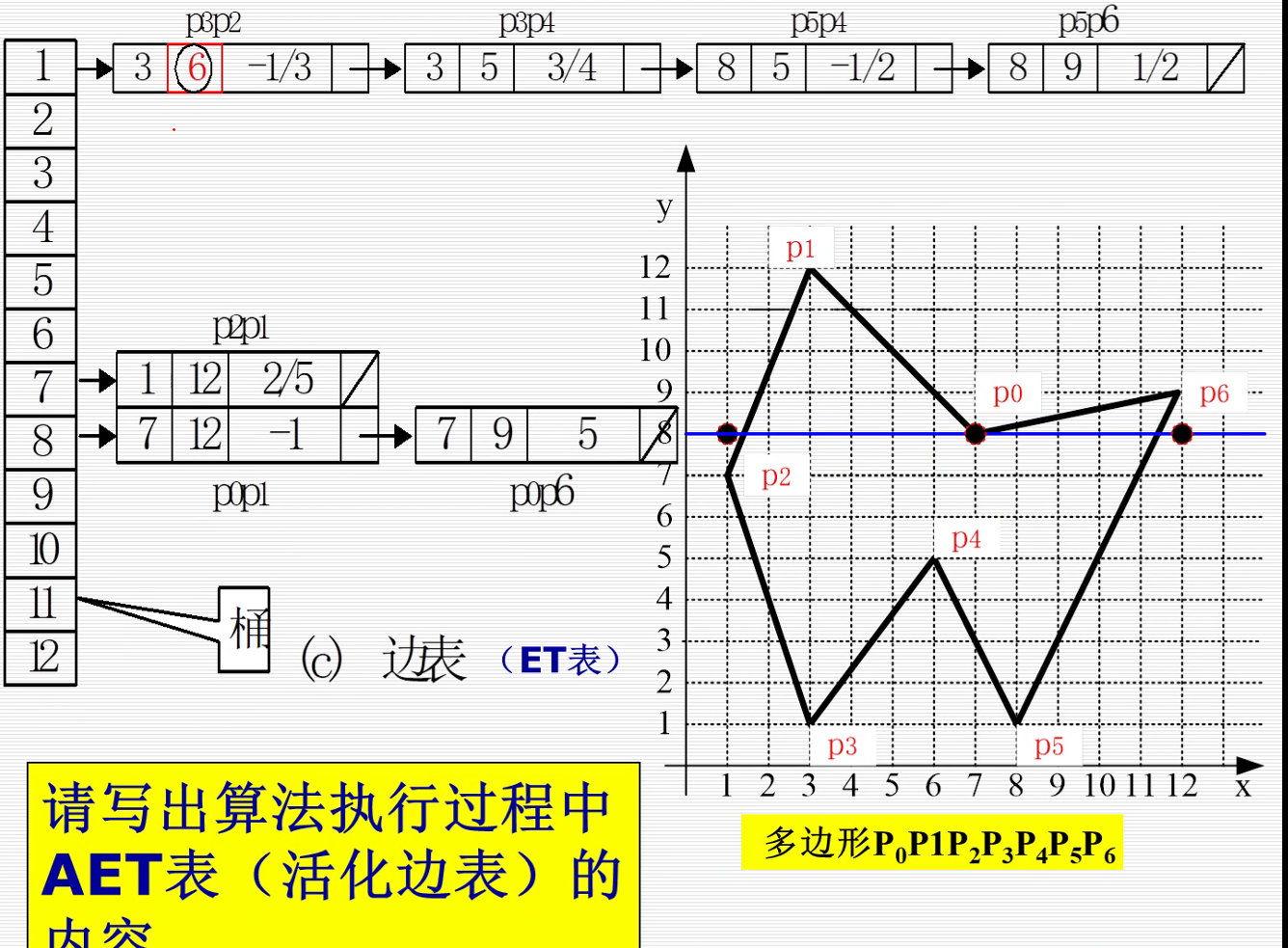
根据建立的边表,改进有效边表(活化边表)的算法步骤如下:
(1)初始化:构造边表,AET表置空;
(2)将第一个不空的ET表中的边与AET表合并;
(3)由AET表中取出交点对进行填充。填充之后删除y=ymax的边;
(4)yi+1=yi+1,根据xi+1=xi+1/k计算并修改AET表,同时合并ET表中y=yi+1桶中的边,按次序插入到AET表中,形成新的AET表;
(5)AET表不为空则转(3),否则结束。
3.边缘填充算法
基本思想:按任意顺序处理多边形的每条边。处理时,先求出该边与扫描线的交点,再对扫描线上交点右方的所有像素取反。
特点:算法简单,但对于复杂图型,每一像素可能被访问多次。
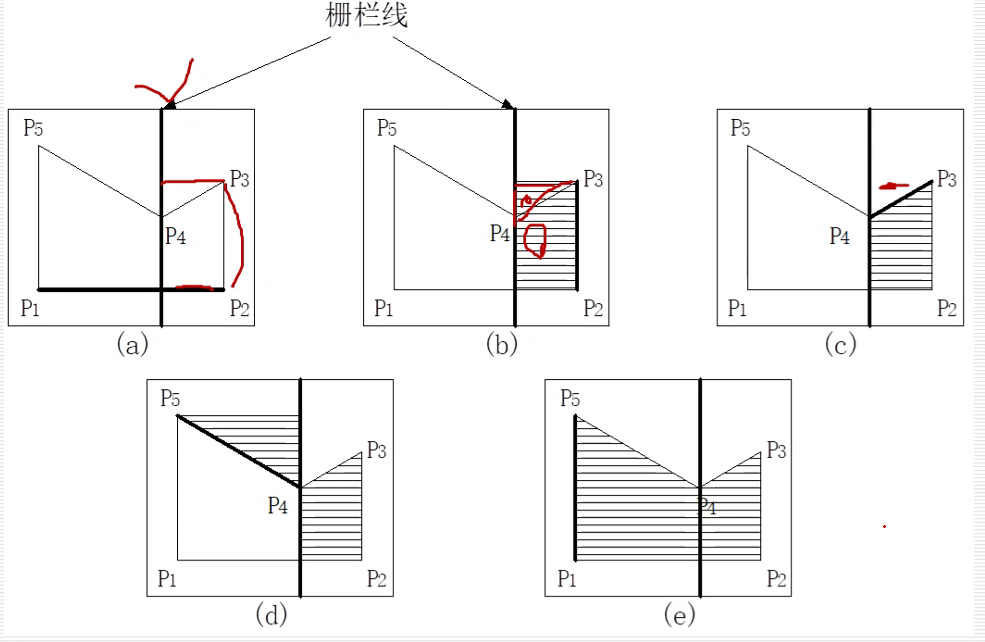
4.栅栏填充算法
栅栏指的是一条过多边形顶点且与扫描线垂直的直线。它把多边形分为两半。
基本思想:按任意顺序处理多边形的每一条边,但处理每条边与扫描线的交点时,将交点与栅栏之间的像素取反。
特点:这种算法尽管减少了被重复访问像素的数目,但仍有一些像素被重复访问。
5.边标志算法
基本思想:先用特殊的颜色在帧缓存中将多边形的边界勾画出来,然后将着色的像素点依x坐标递增的顺序配对,再把每一对像素构成的区间置为填充色。
操作分为两个步骤:
(1)打标记:对多边形的每条边进行直线扫描转换。
(2)填充:对每条与多边形相交的扫描线,依从左到右的顺序,按“左闭右开”的原则对扫描线上的像素点进行填色。
特点:当用软件实现本算法时,速度与改进的有效边表算法相当,但本算法用硬件实现后速度会有很大提高。
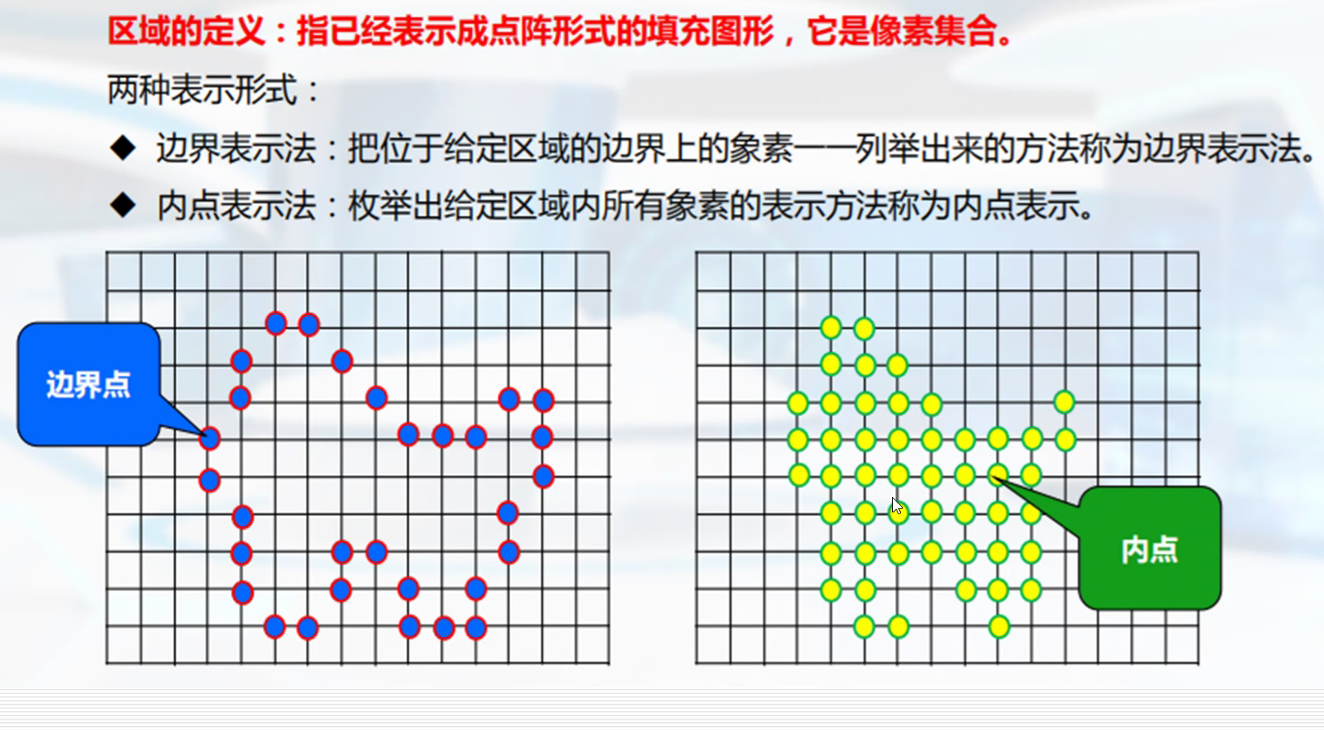
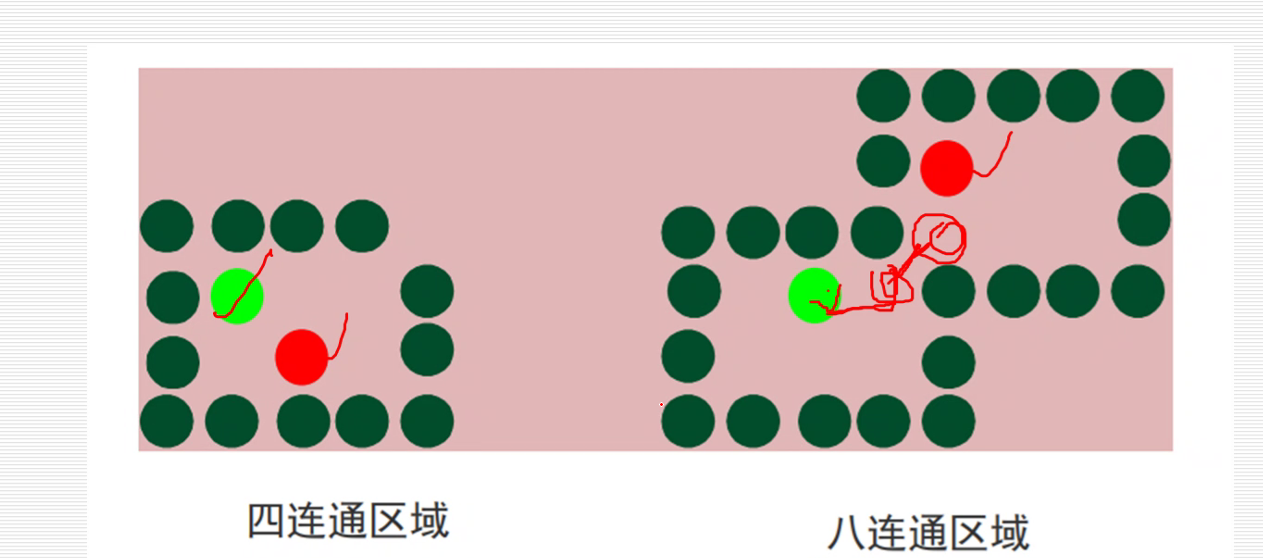
6.区域填充算法

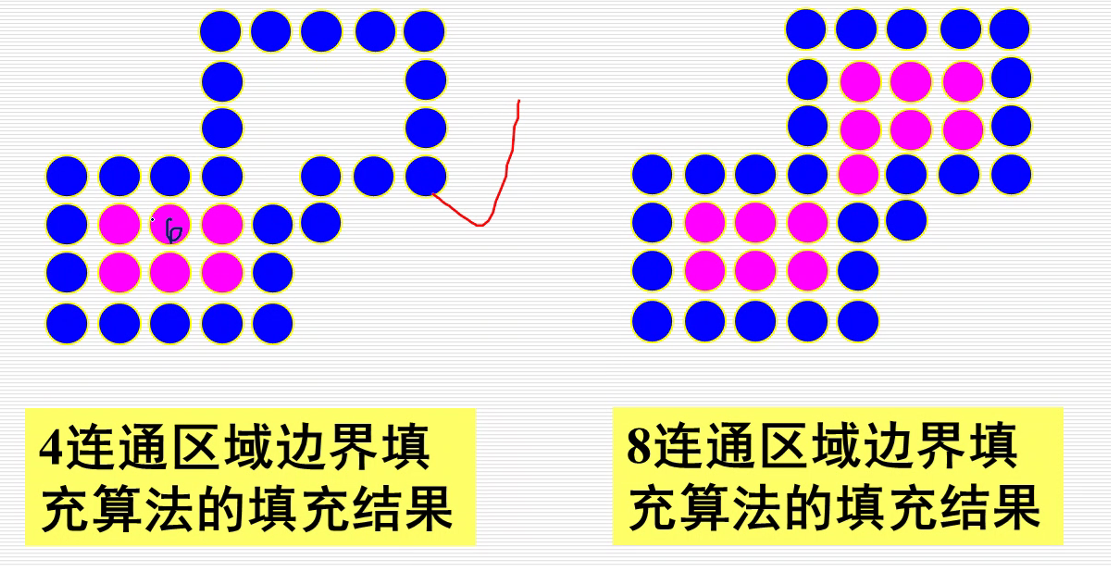
7.简单的种子填充算法

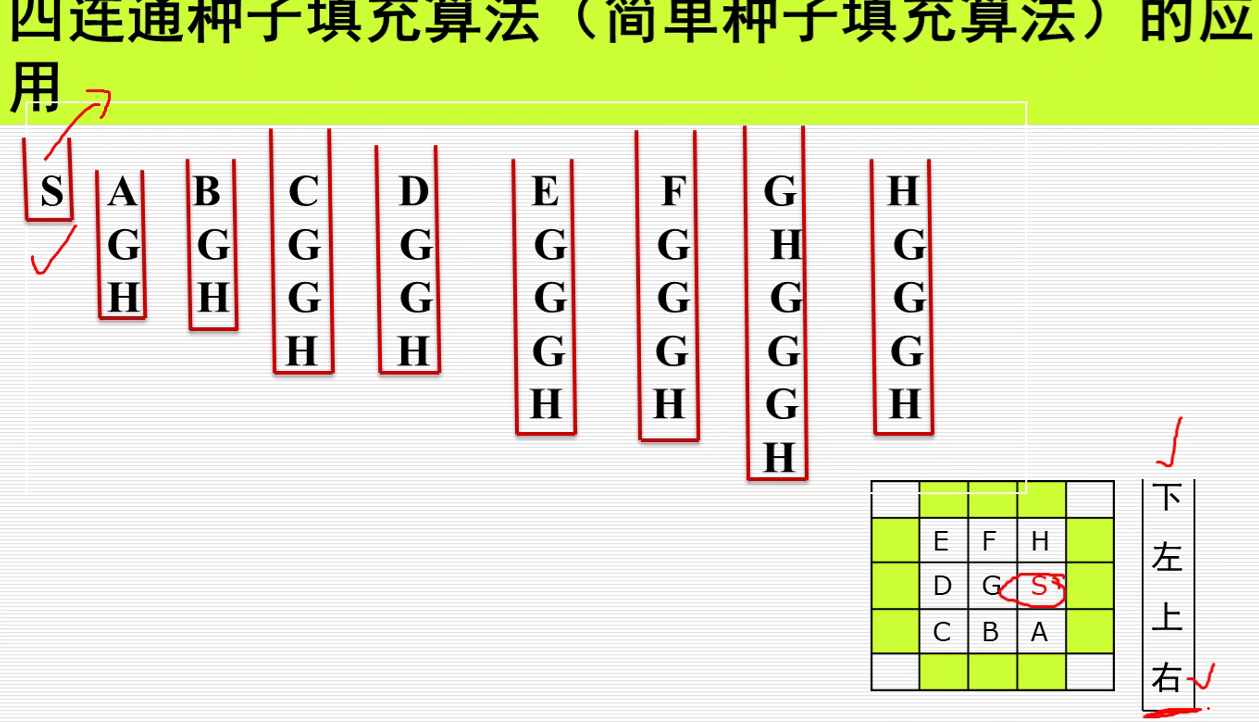
这其实就是个BFS,但是他是不带标记的(出栈的会标记上),所以很多像素会重复入栈。
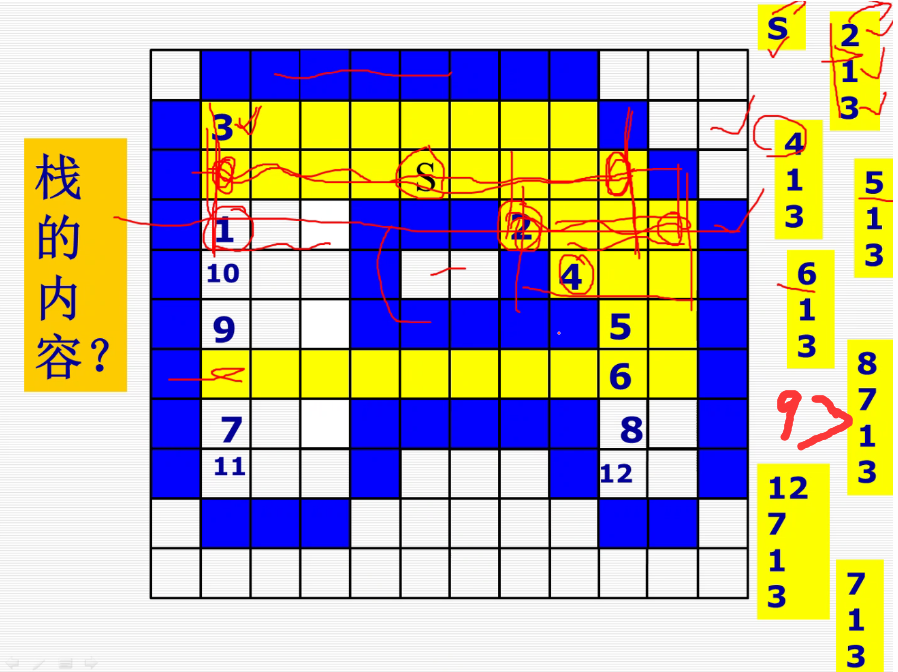
8.扫描线种子填充算法
详细解释:https://blog.csdn.net/orbit/article/details/7343236

9.泛填充算法

其他相关概念:
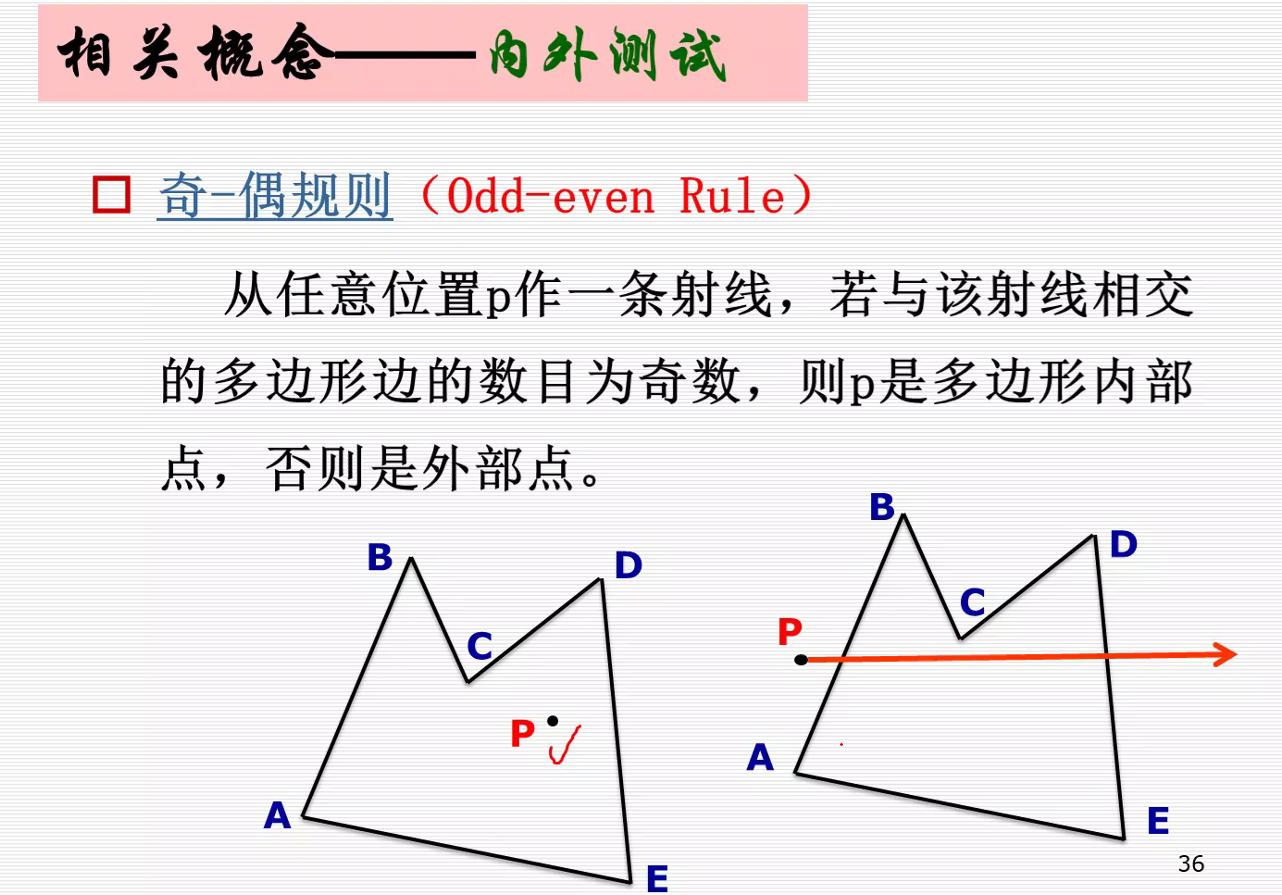
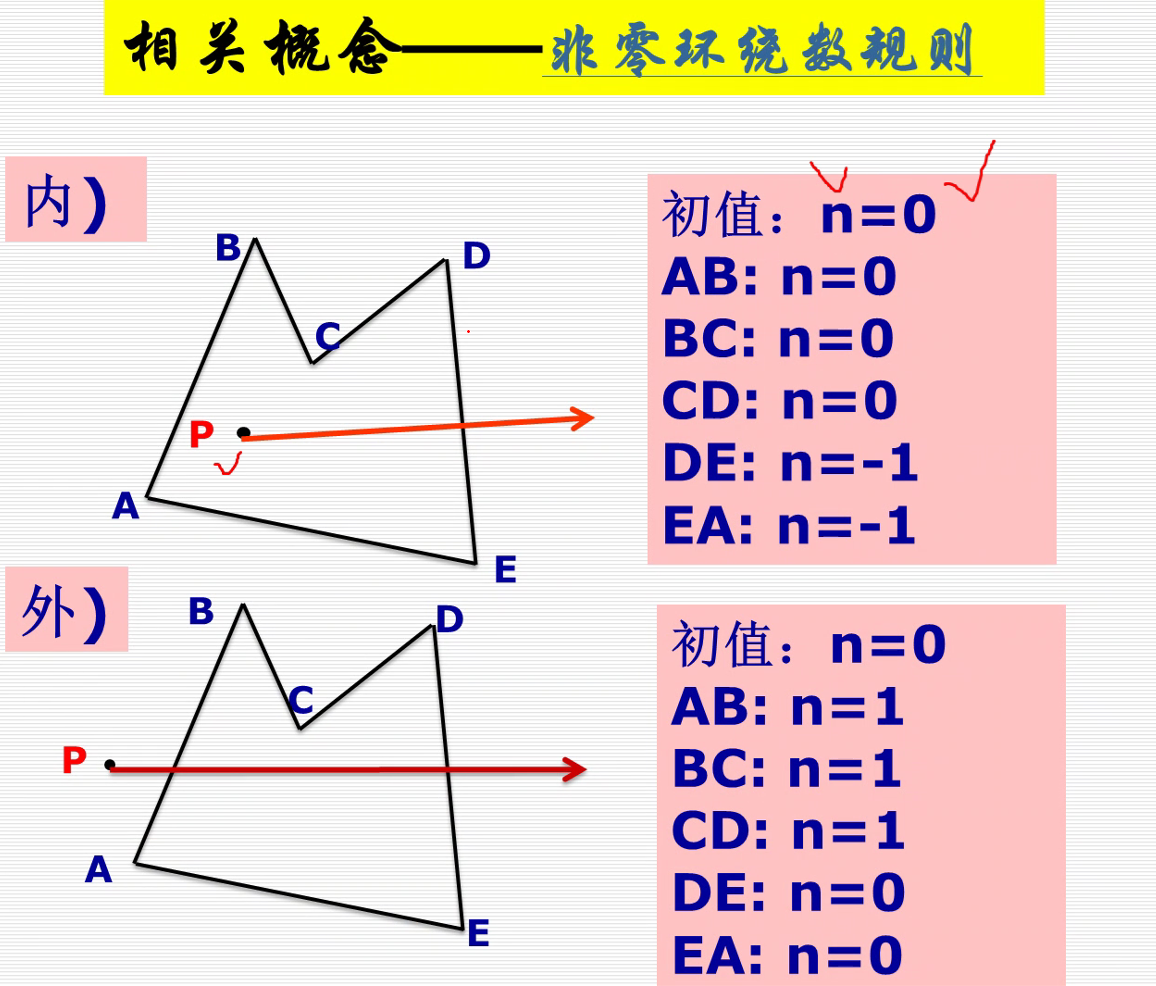
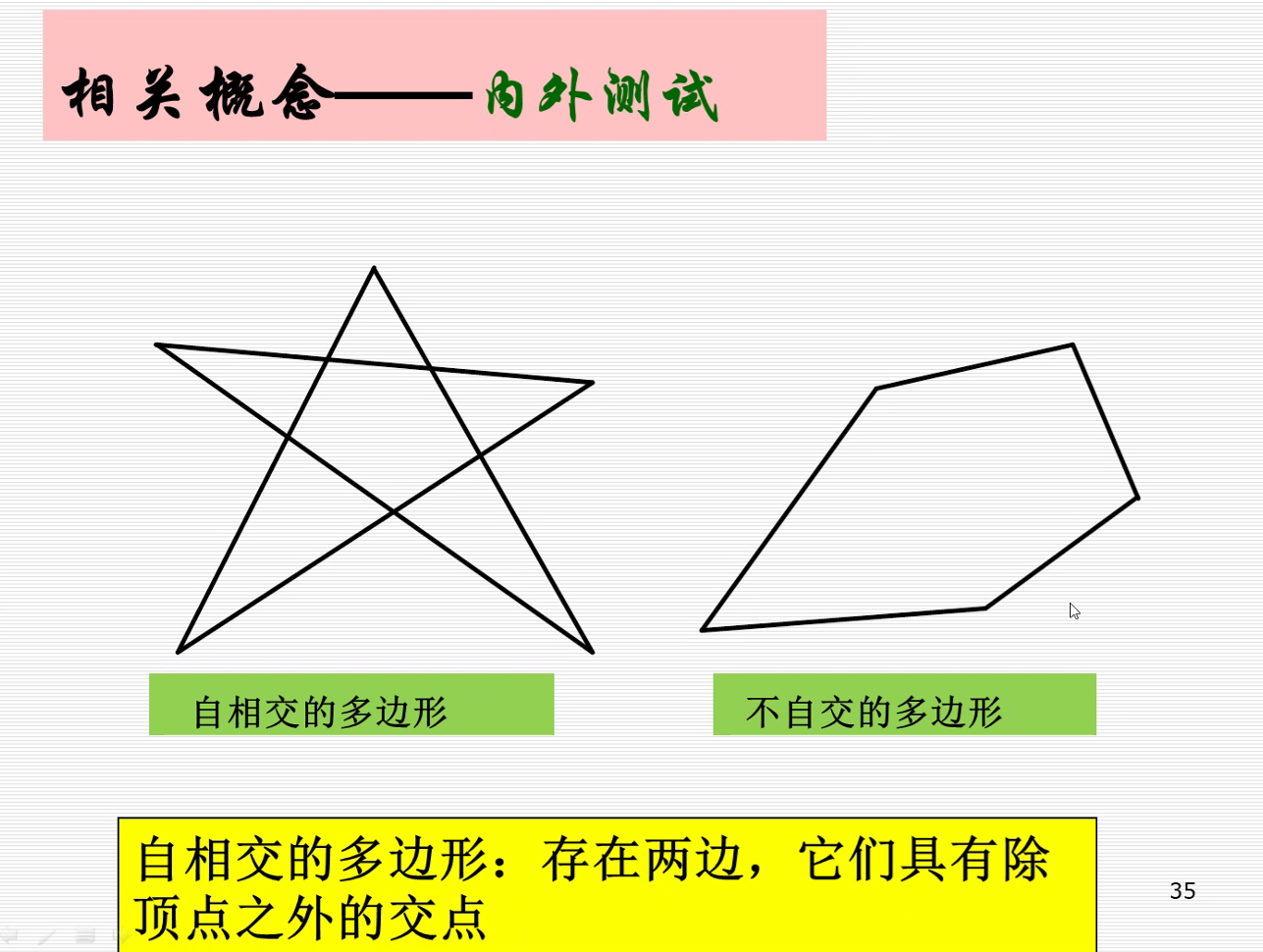
非零环绕数规则:https://www.jianshu.com/p/f1590d4fb5c5

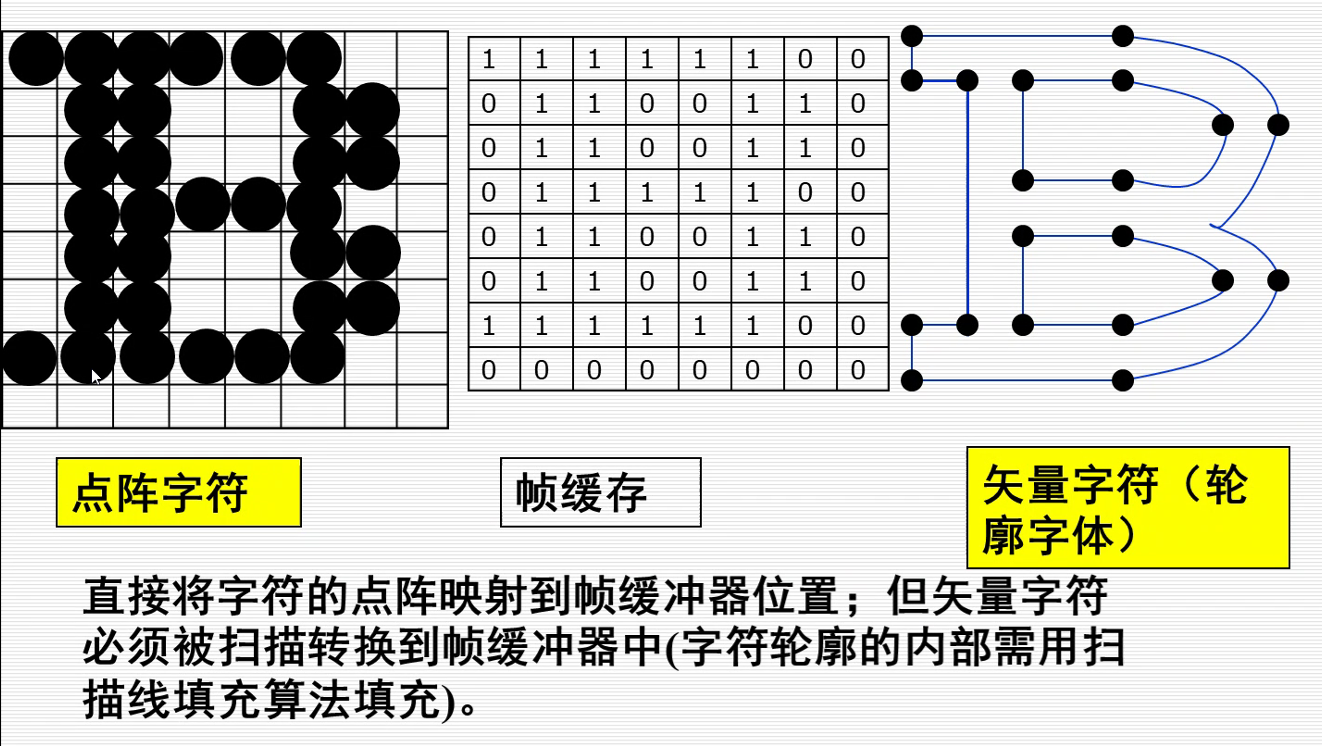
字符处理
属性处理
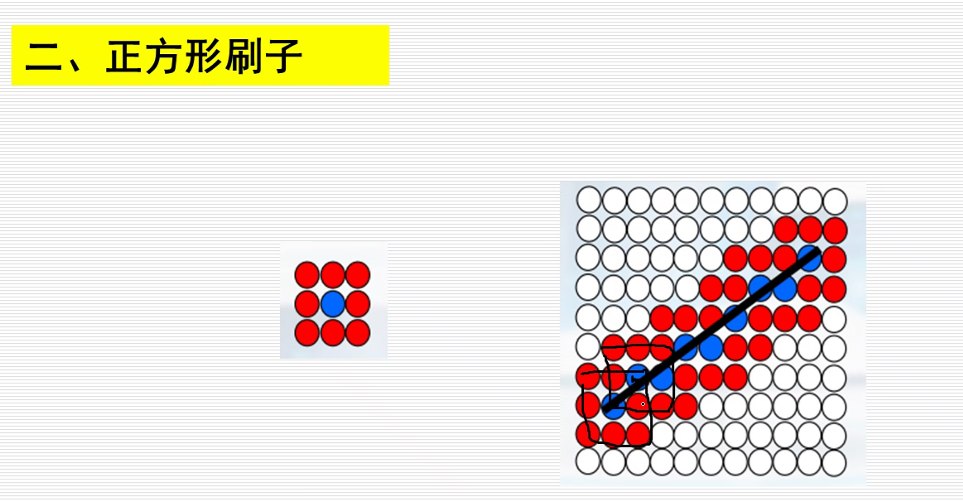
刷子 改变 线条的颜色,线宽。
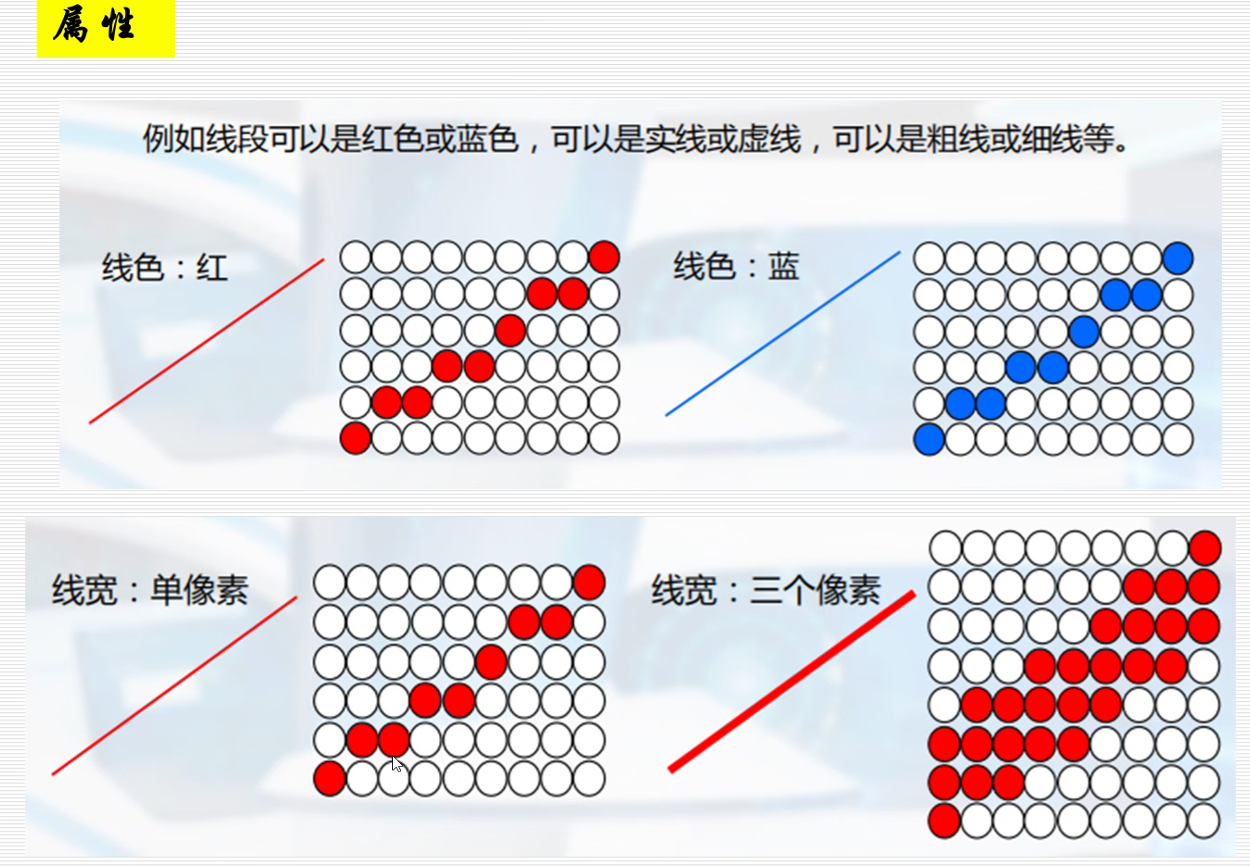
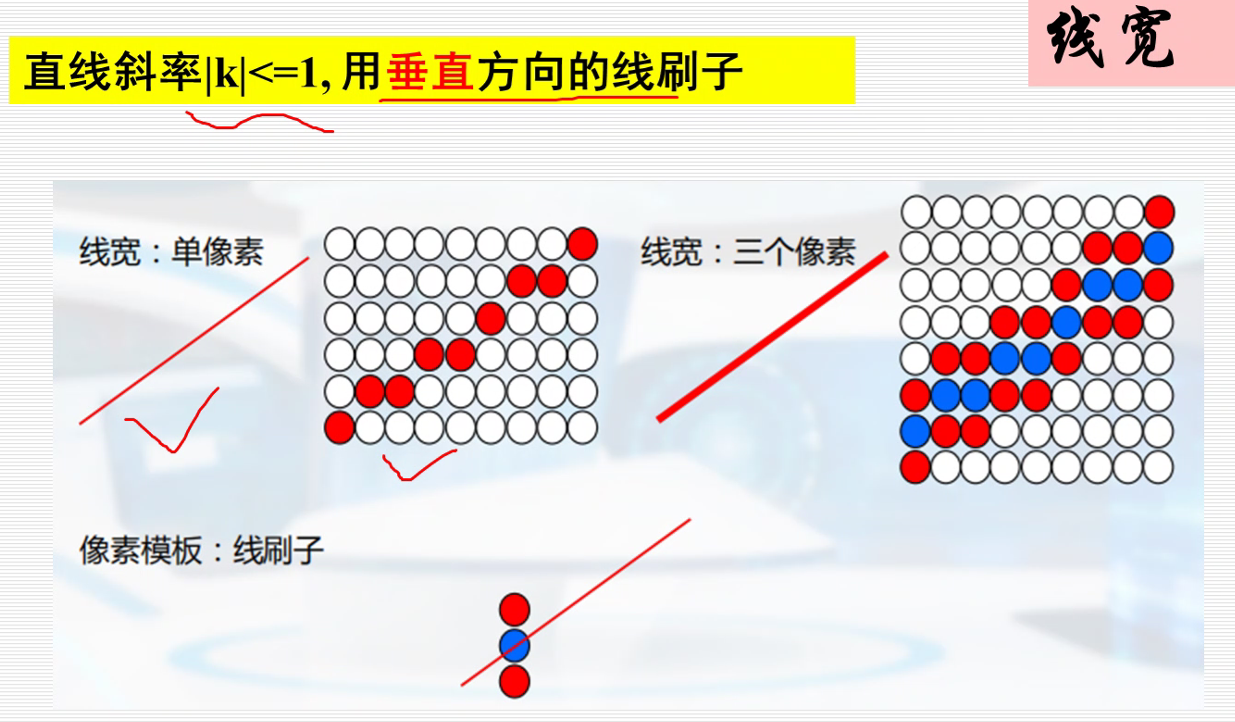
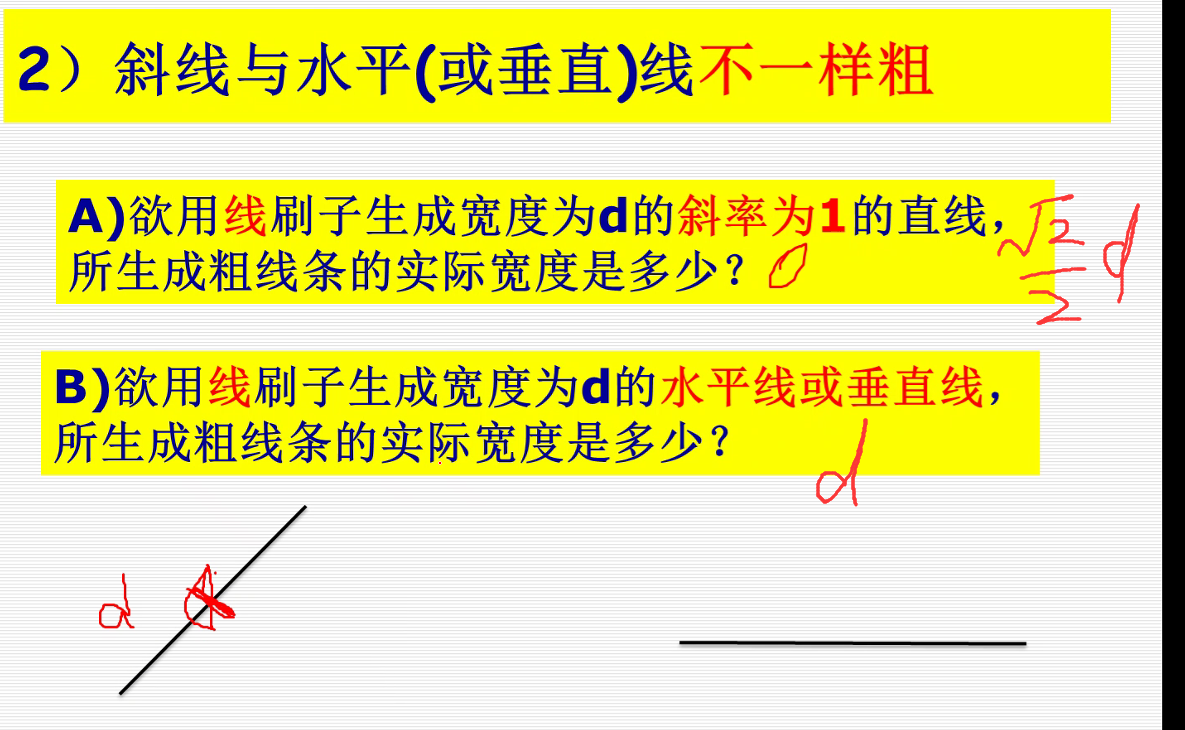
上下各扩展一个,宽度为1就变为宽度为3了。

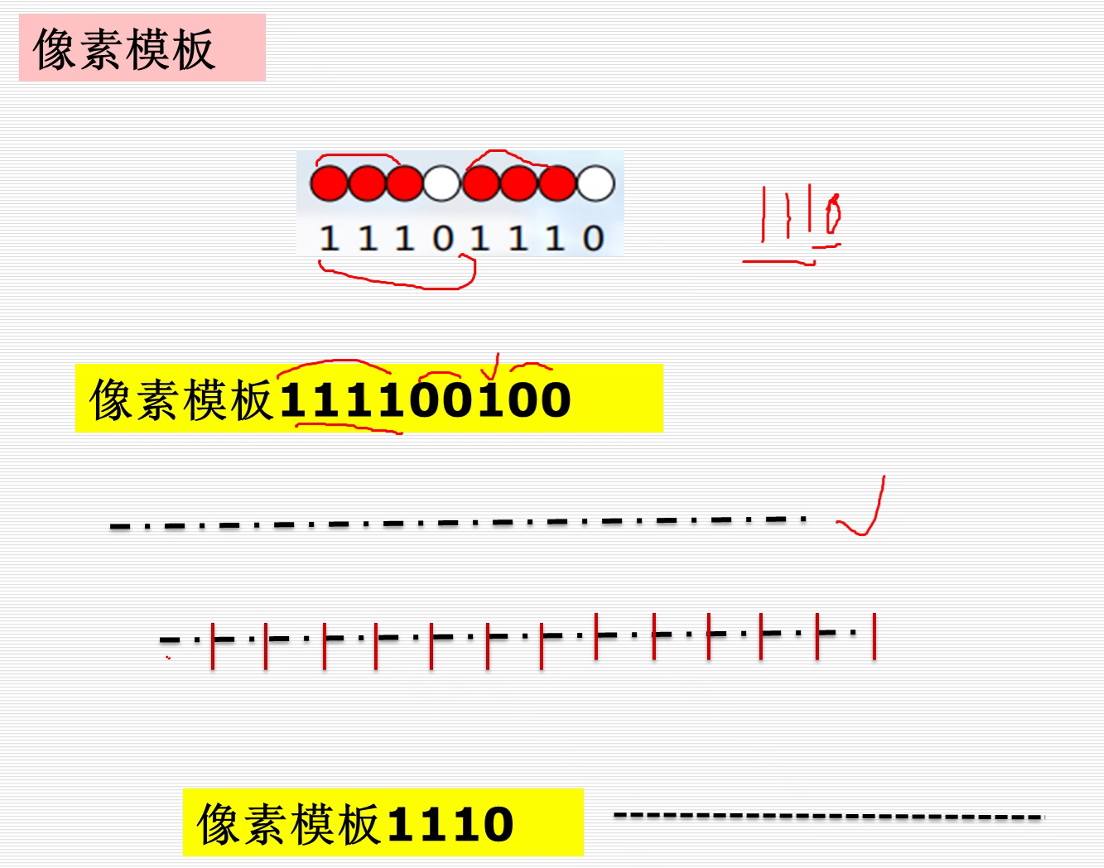
利用 像素模板 改变线形
填充属性:
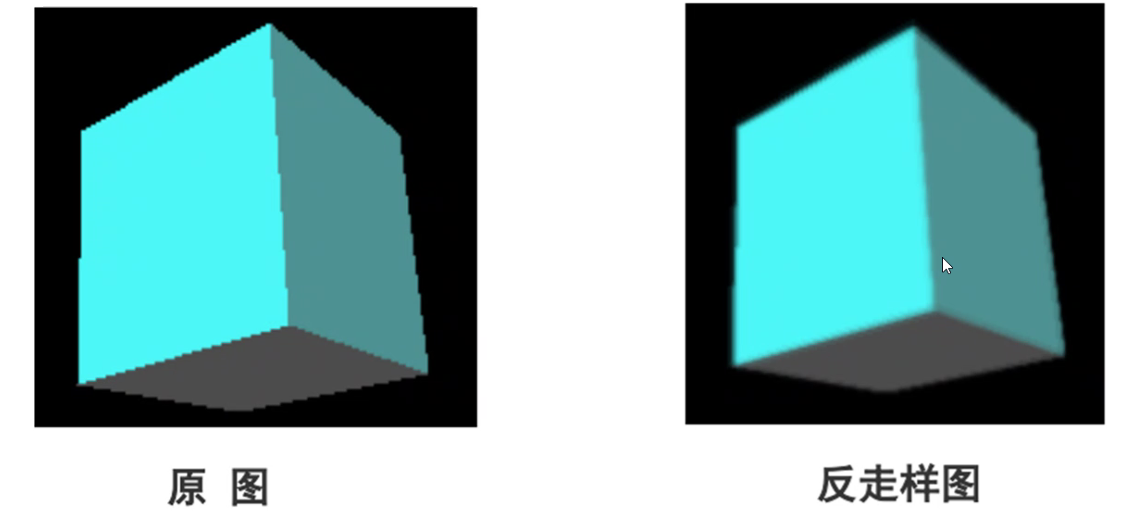
走样现象:

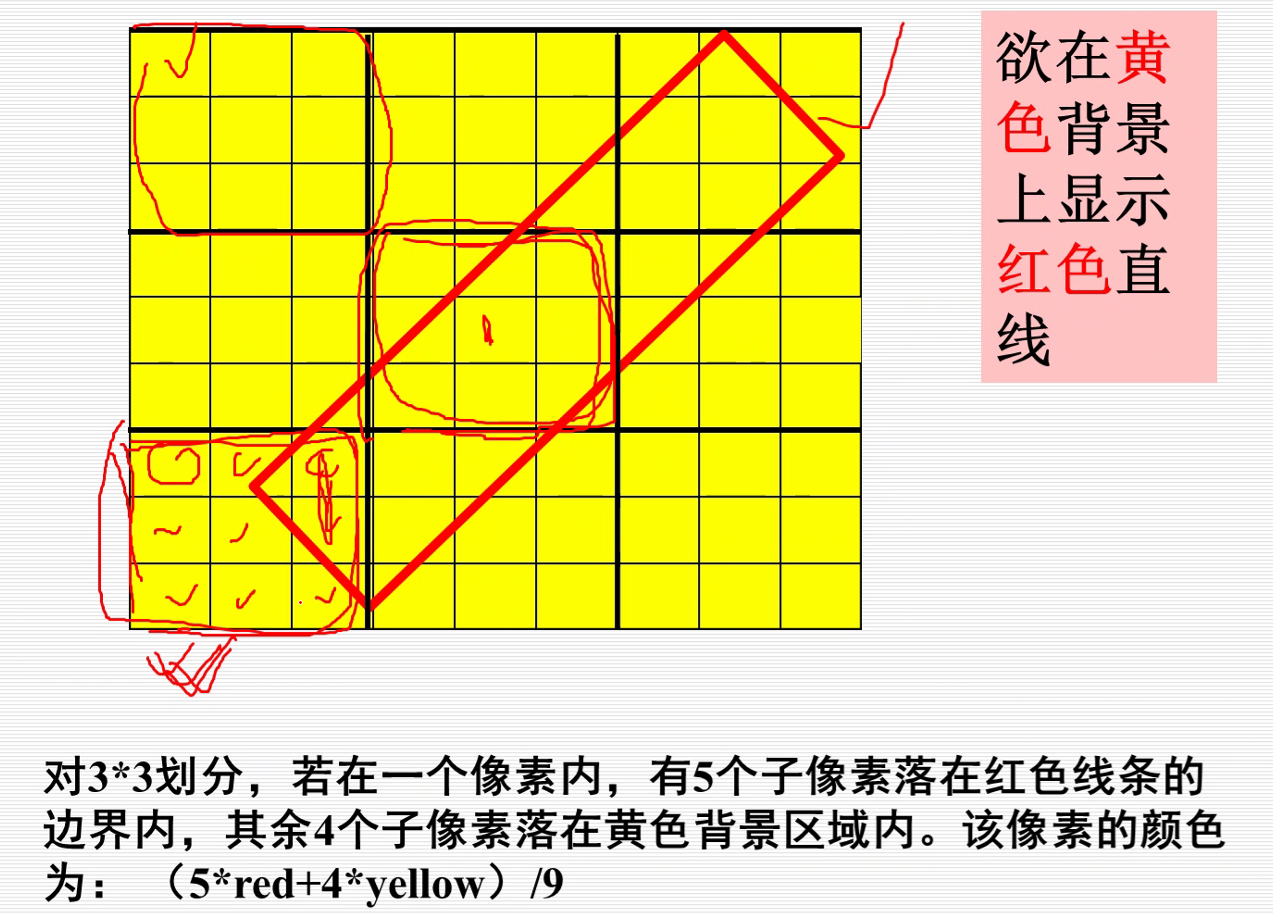
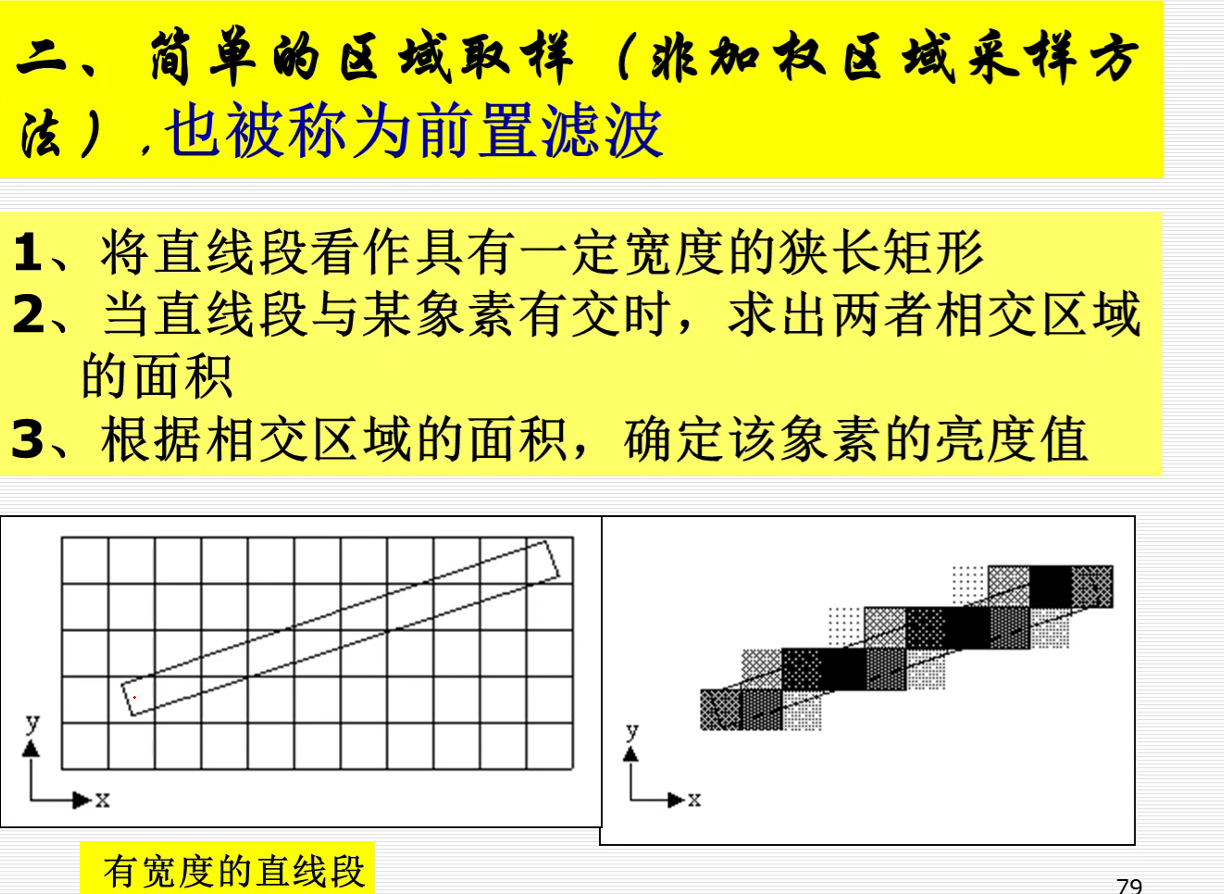
反走样技术:
第六章:二维变换

基本几何变换
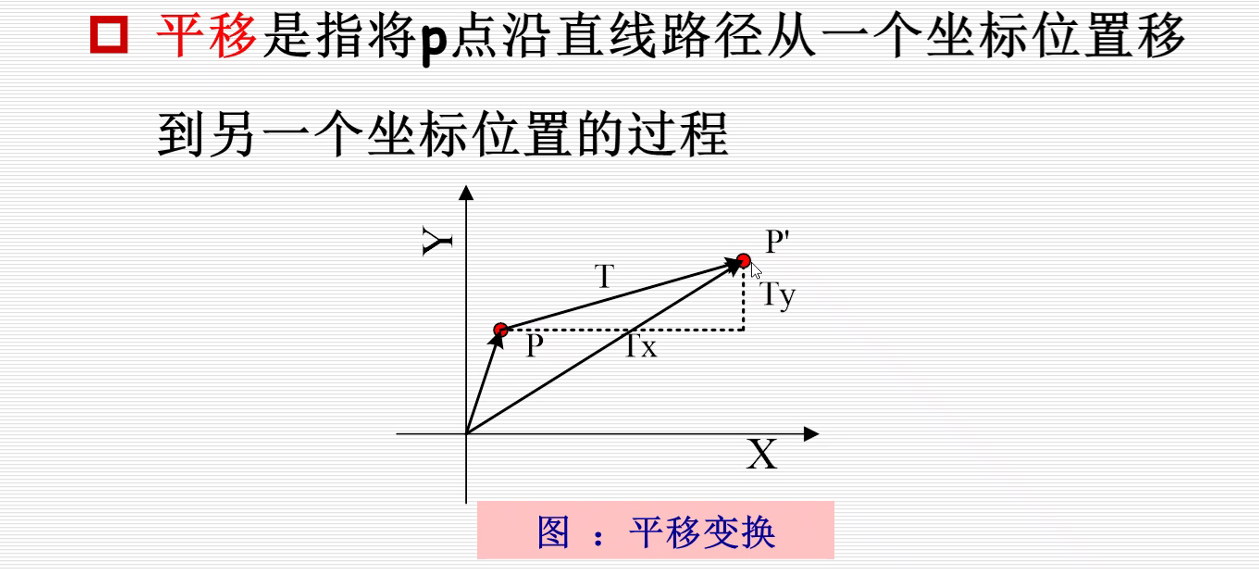
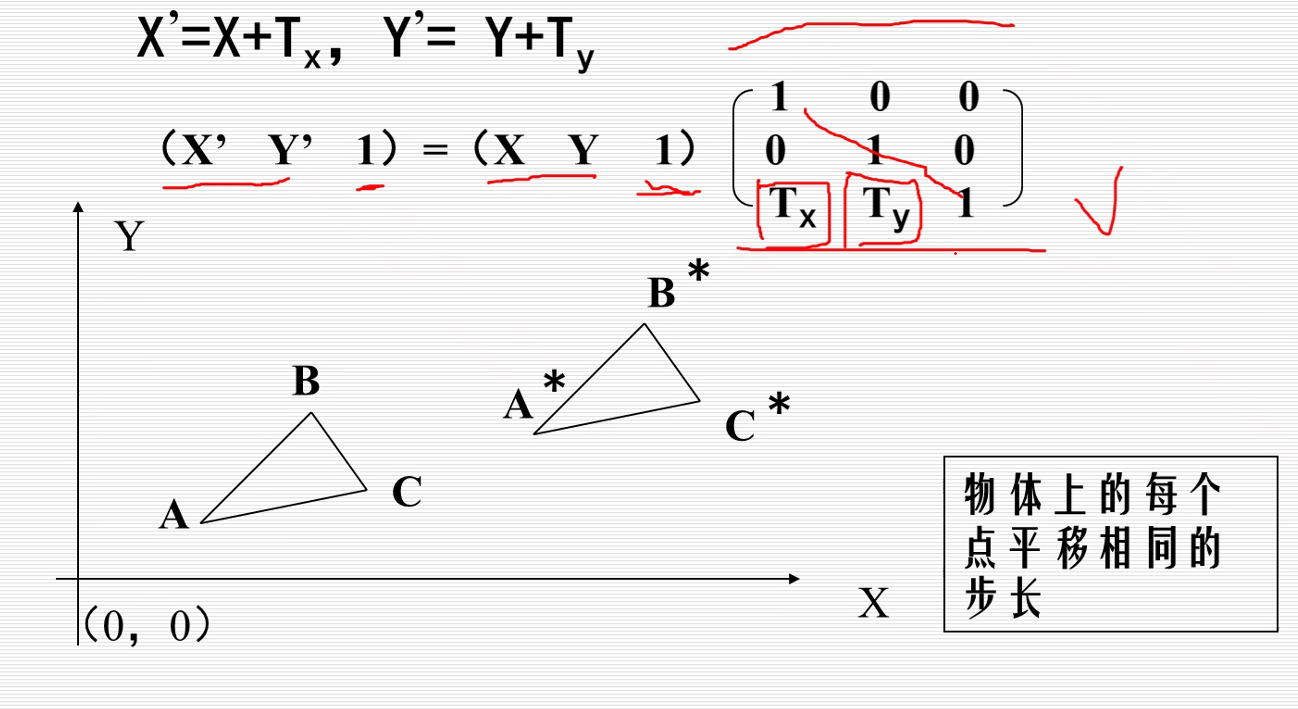
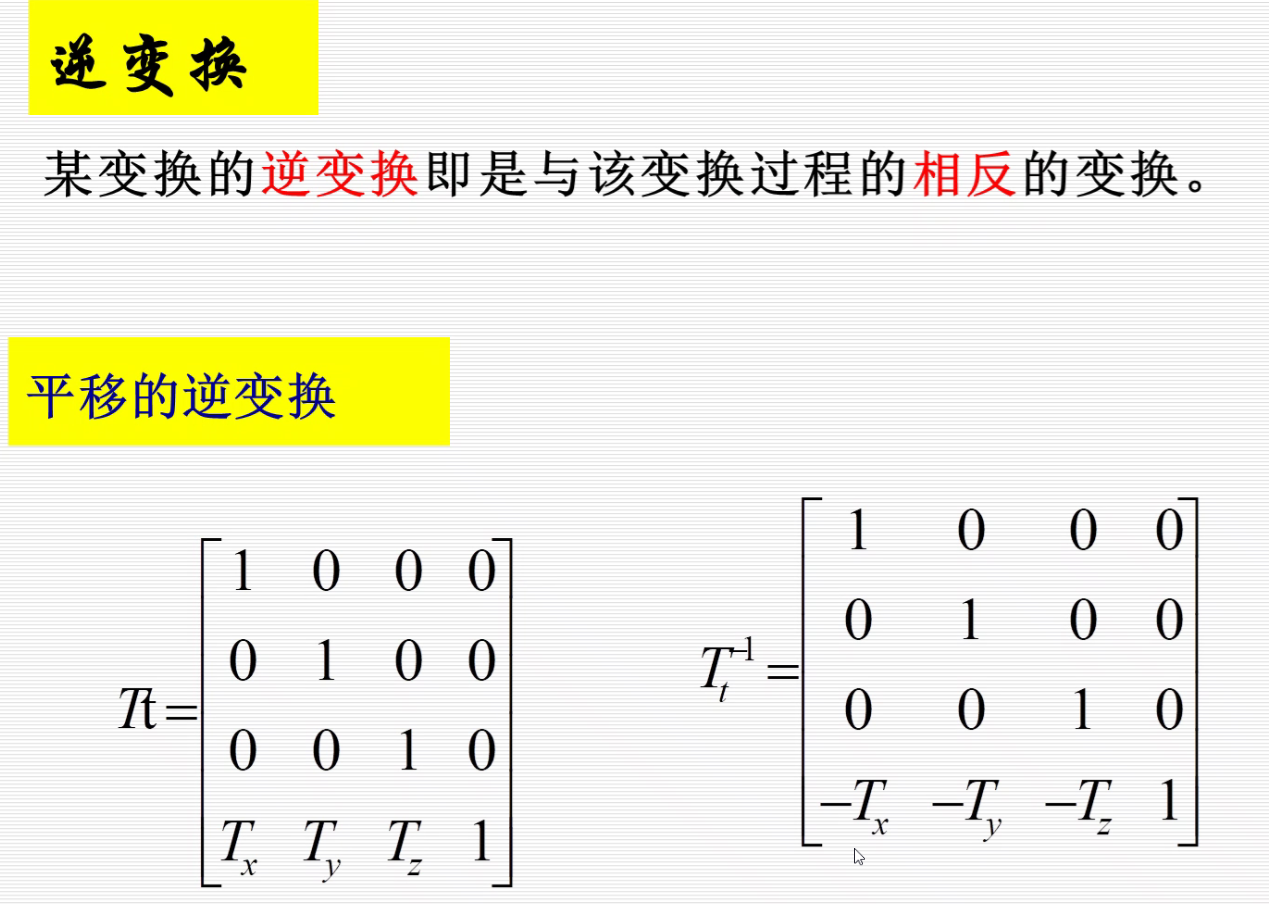
1.平移变换
2.比例变换


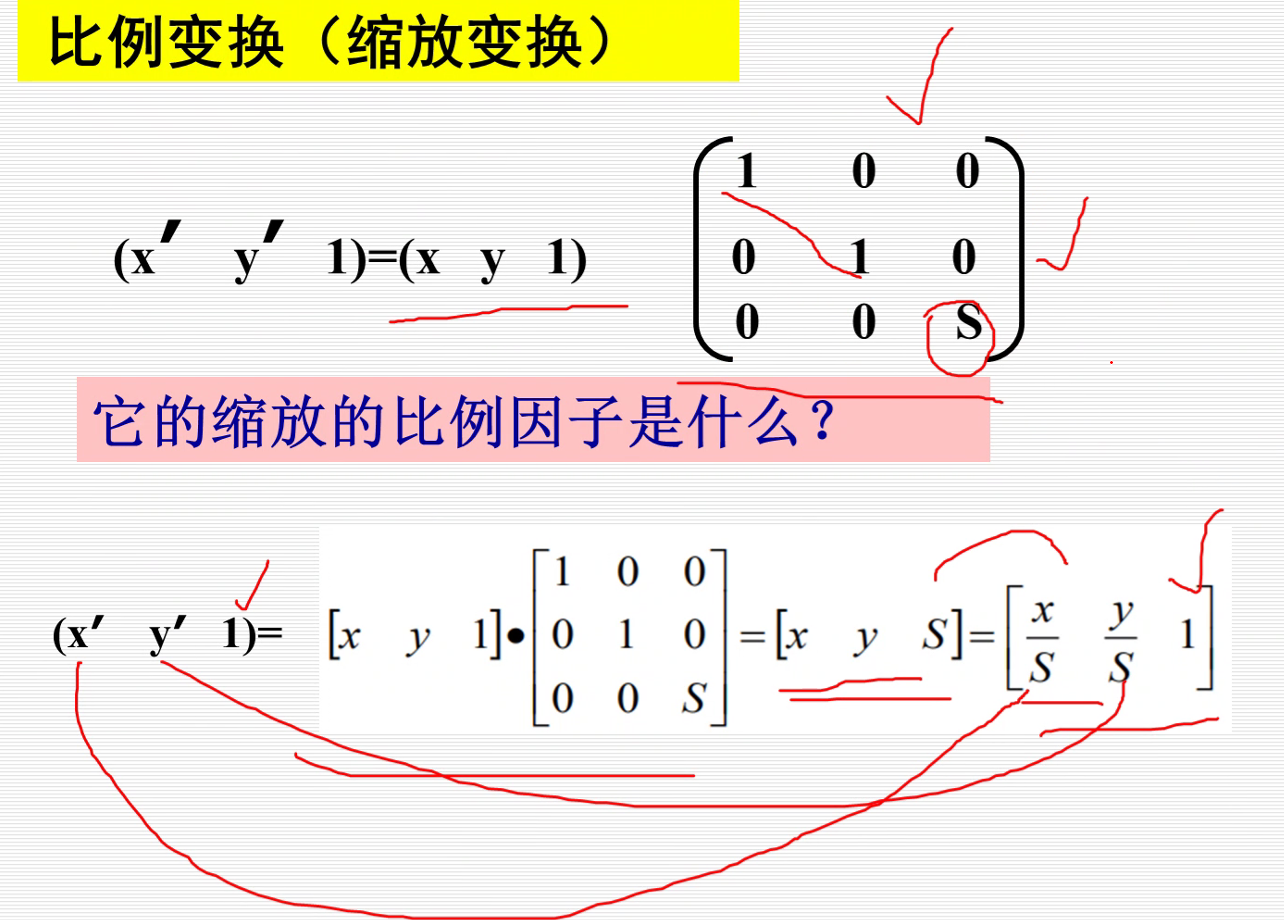
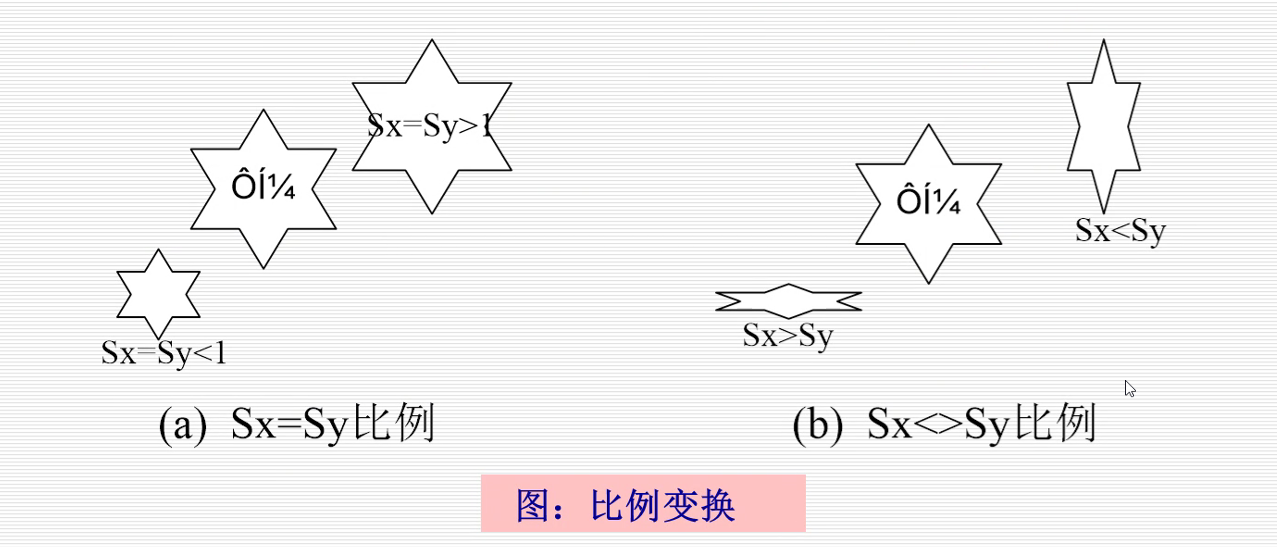
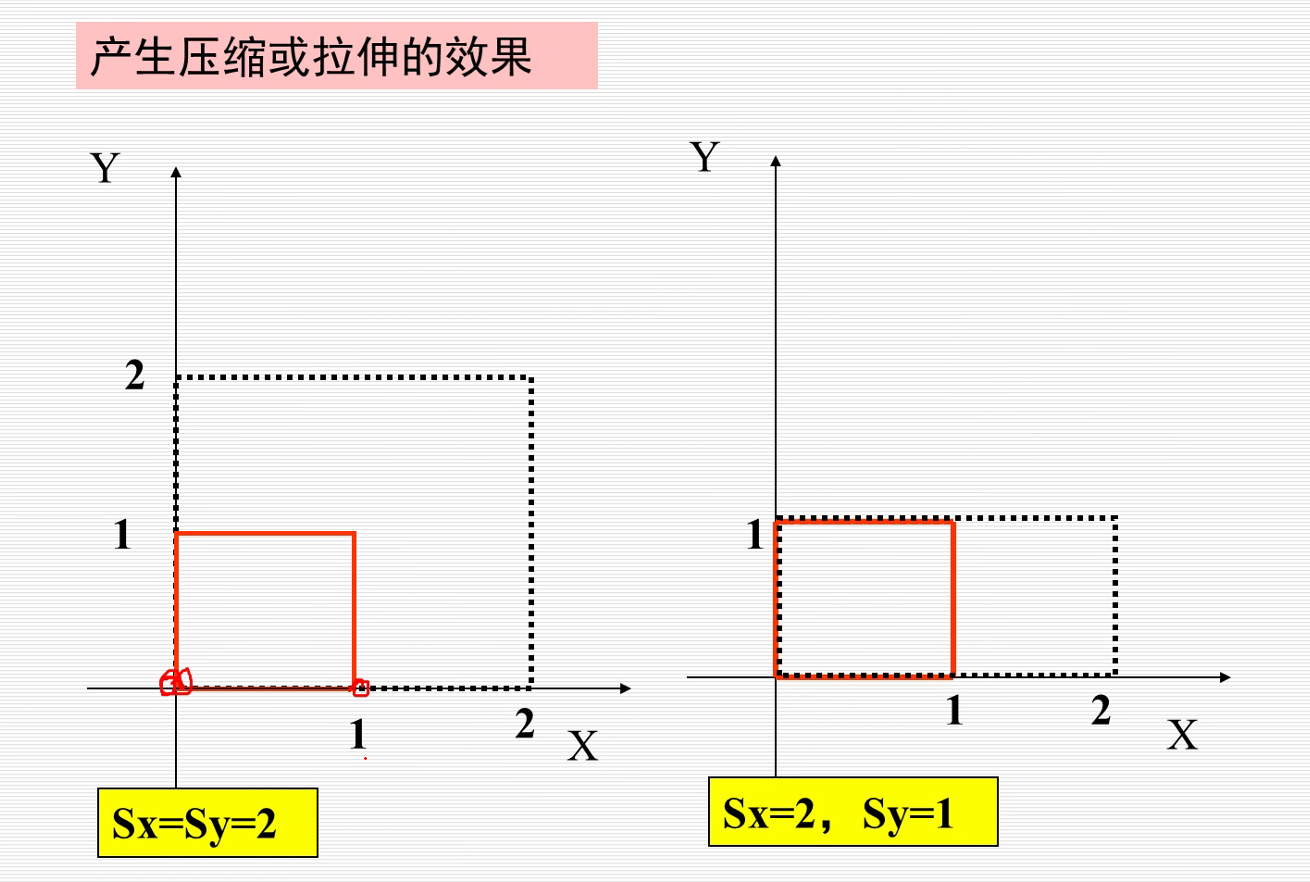
Sx=Sy=2,x和y都扩大2倍
Sx=2,Sy=1,x扩大两倍,y不变。
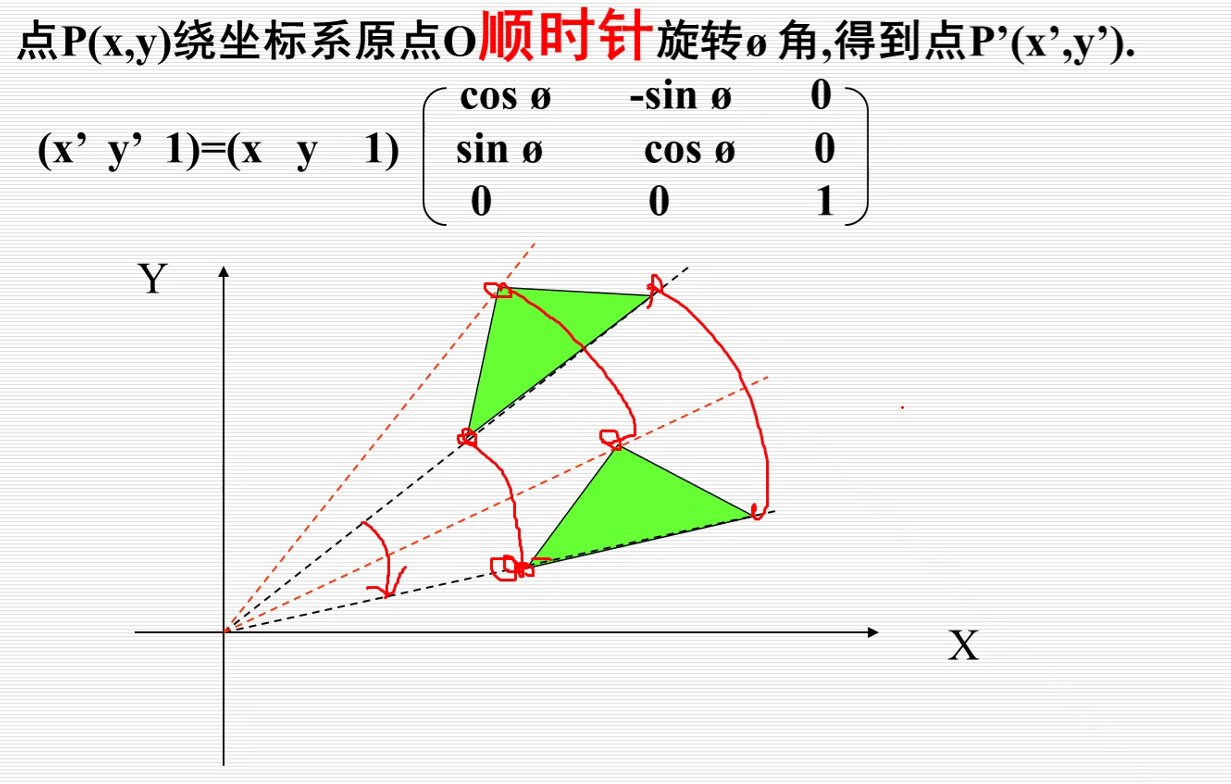
3.旋转变换

4.对称变换
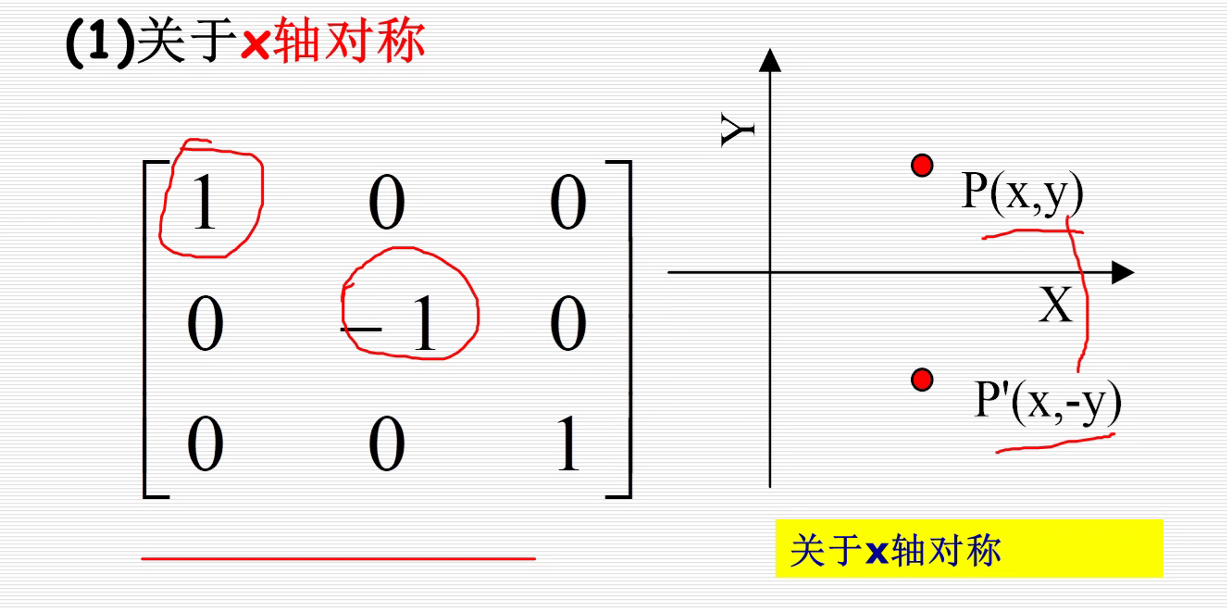
其他的关于什么对称可以先写出坐标,然后对应着找矩阵,就不一一列举了。
5.错切变换
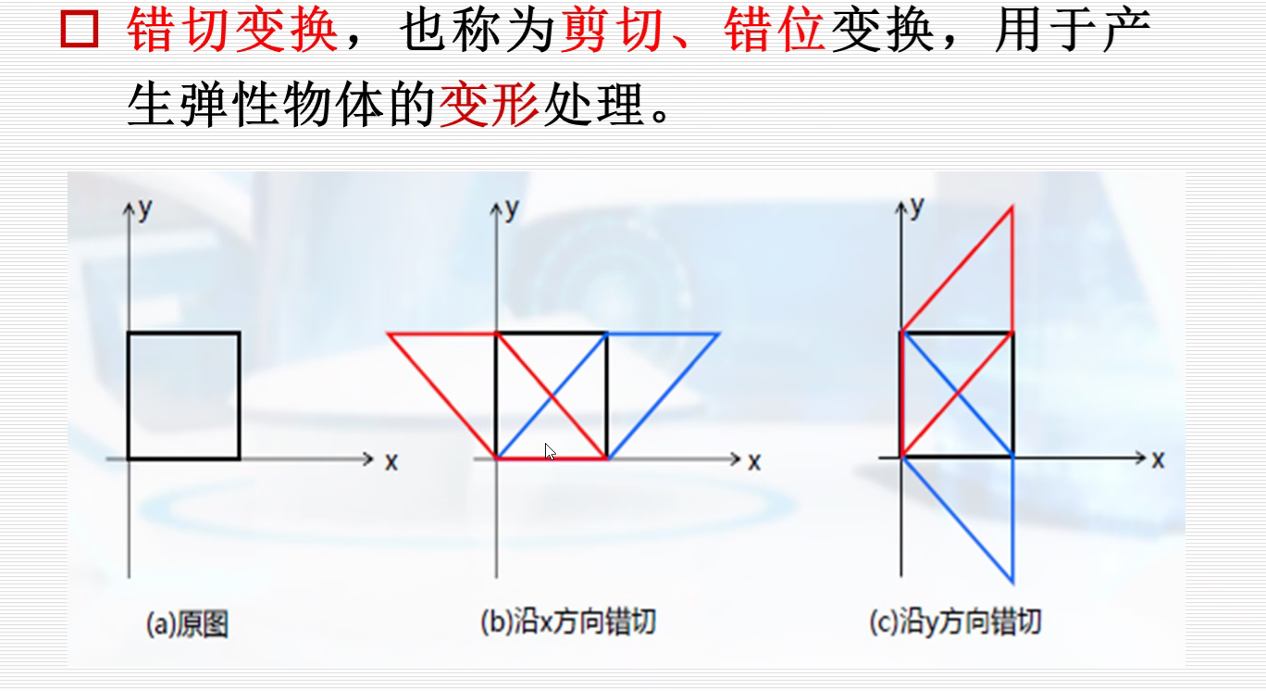
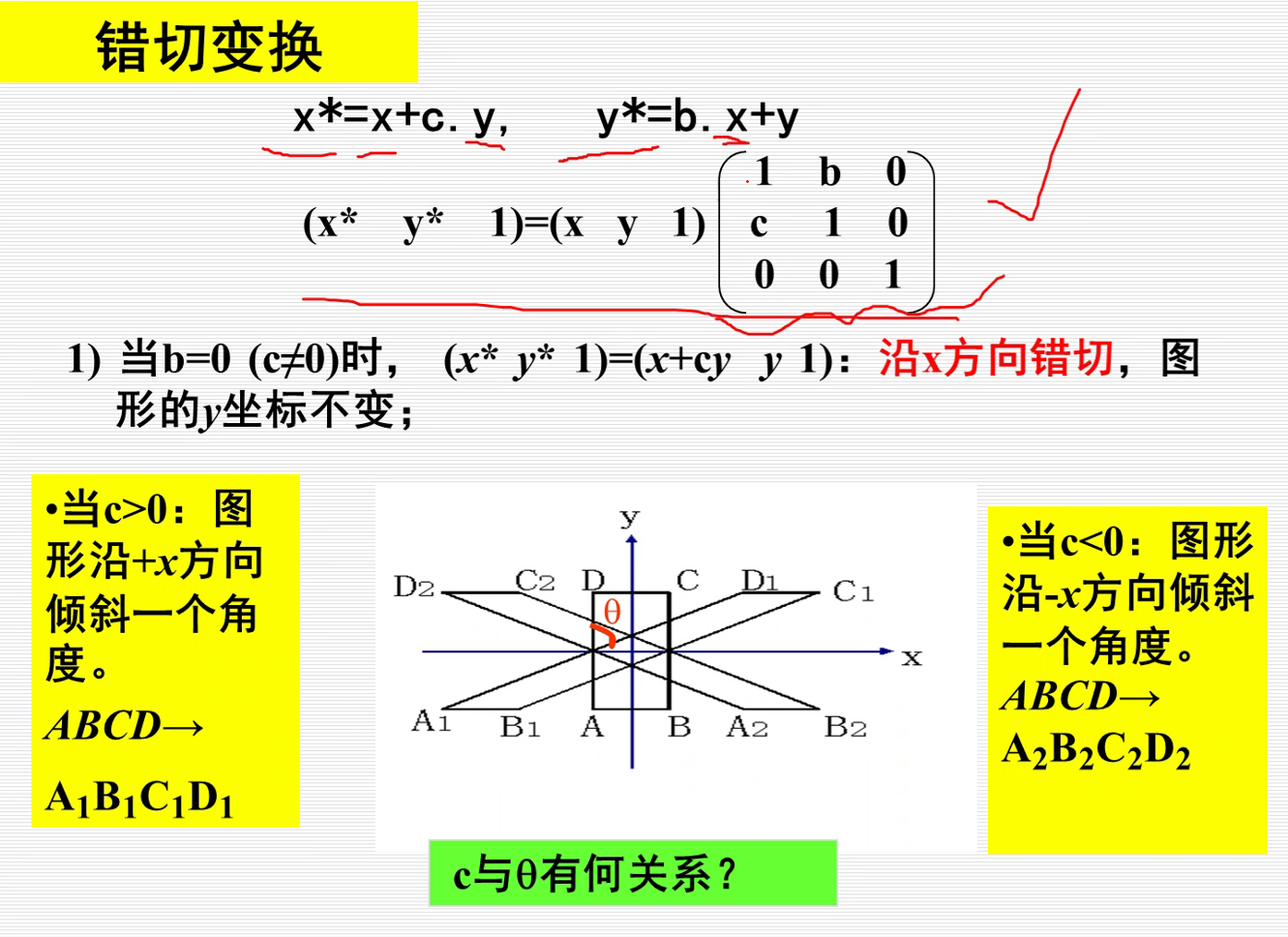
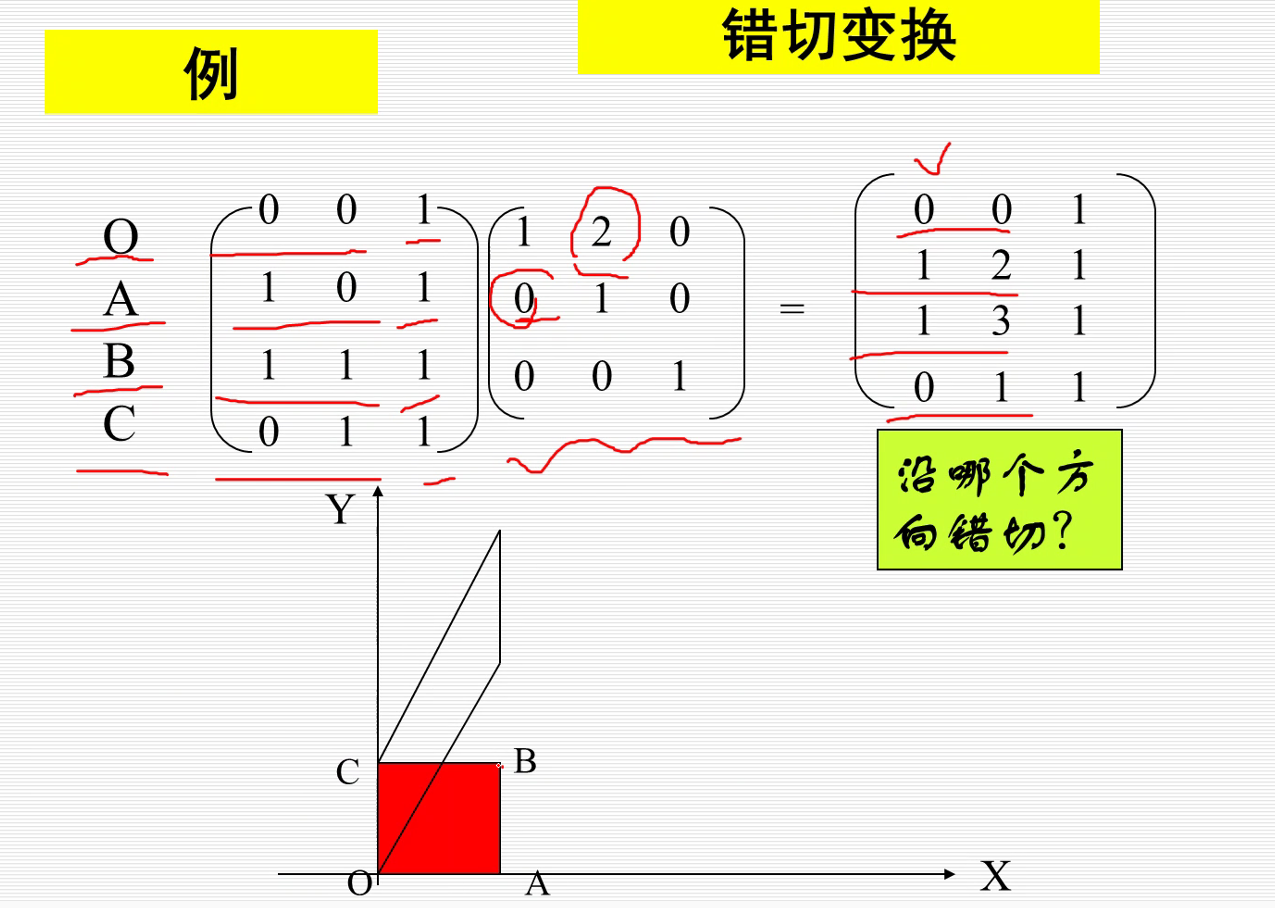
6.复合变换
上面的变换矩阵多个乘在一起就是多个变换的叠加。
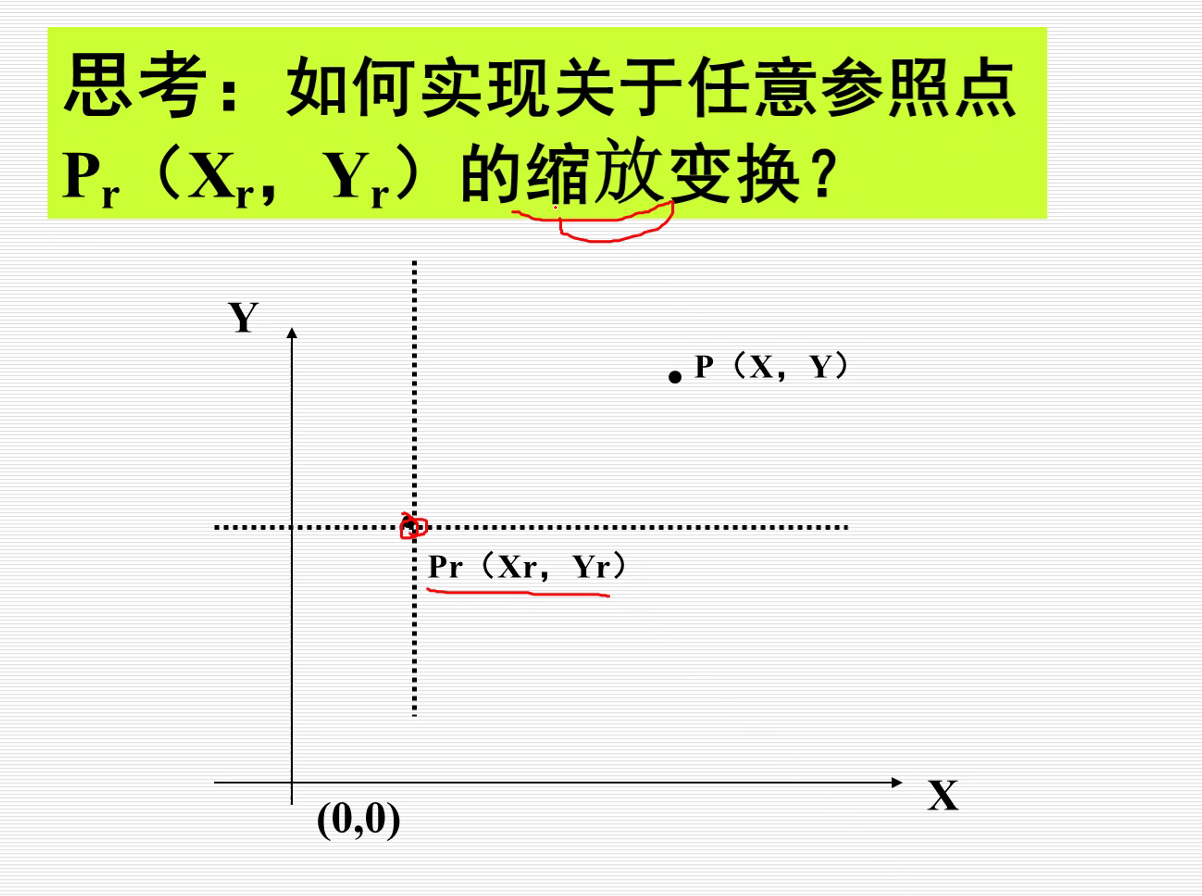
先平移到原点,然后缩放,再平移回去。
如何实现任意参照点的旋转变换? 先平移到原点,然后旋转,再平移回去。
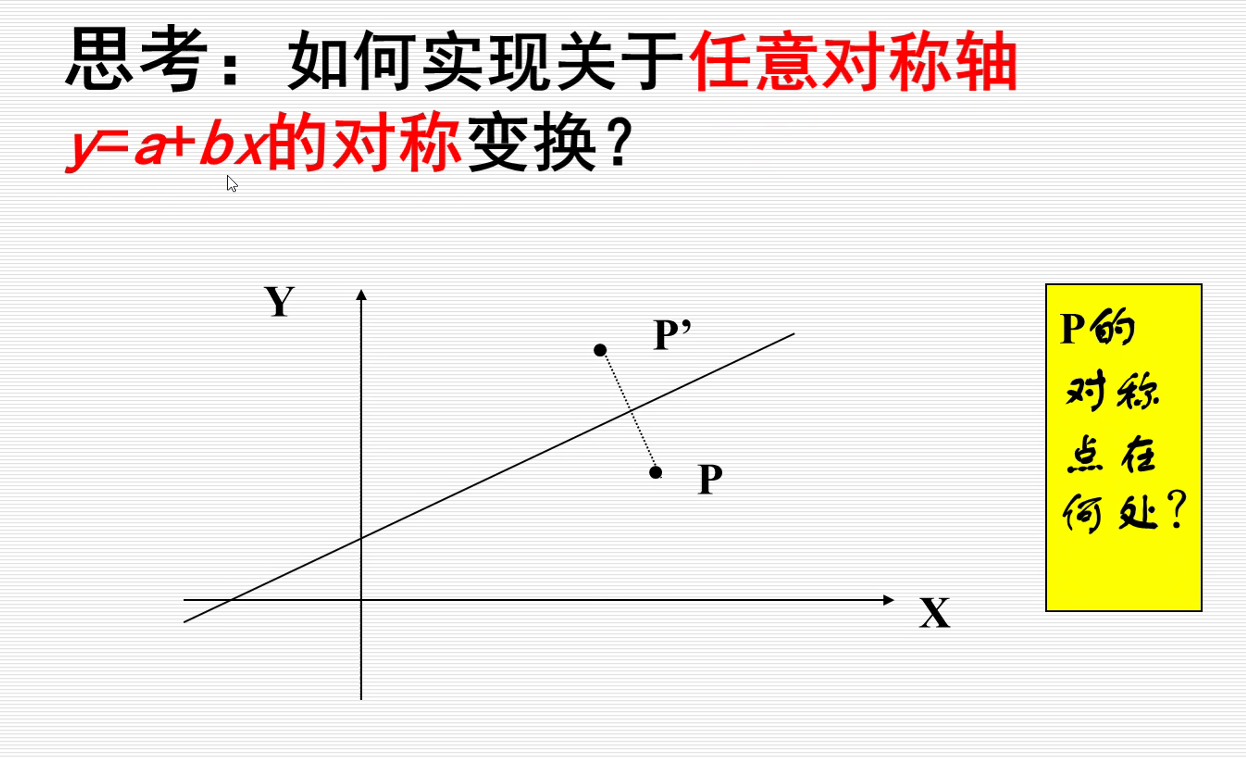
先向右平移,然后旋转theta角,关于y对称过去成p’,然后反转回来theta角,最后左平移回去。
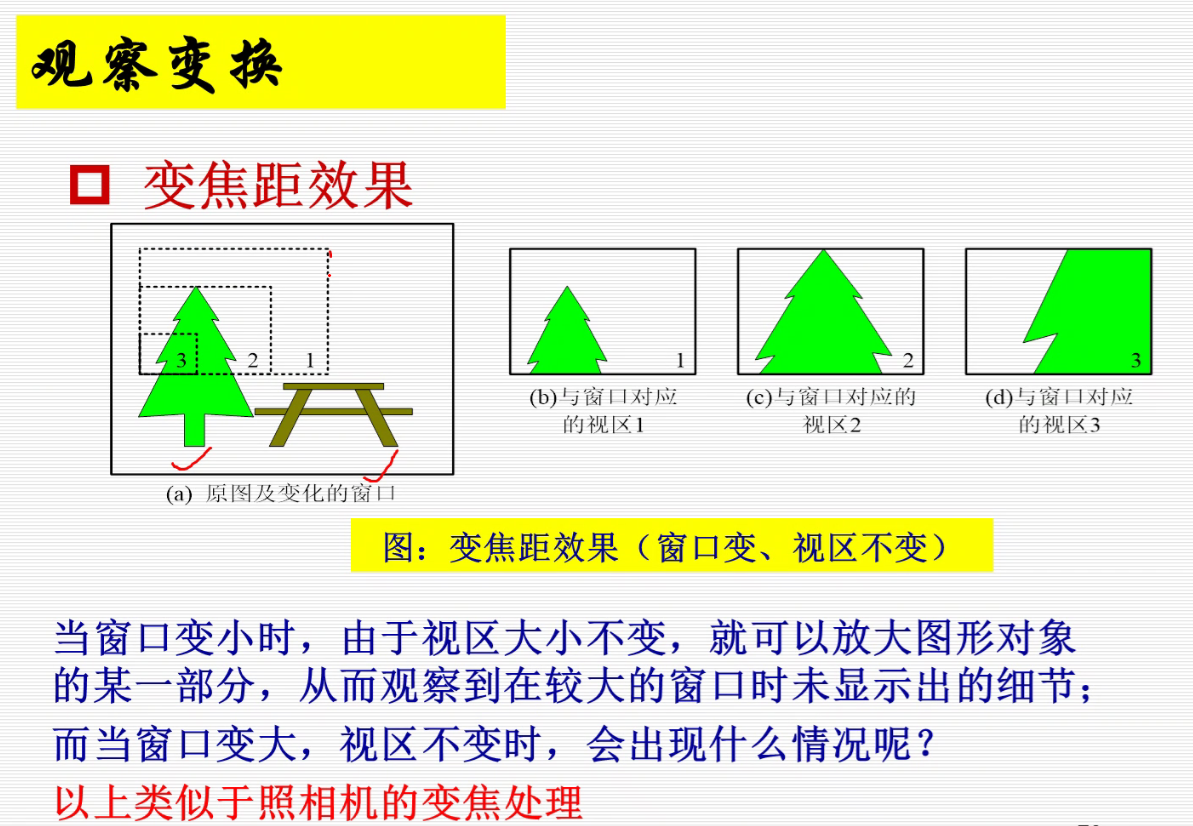
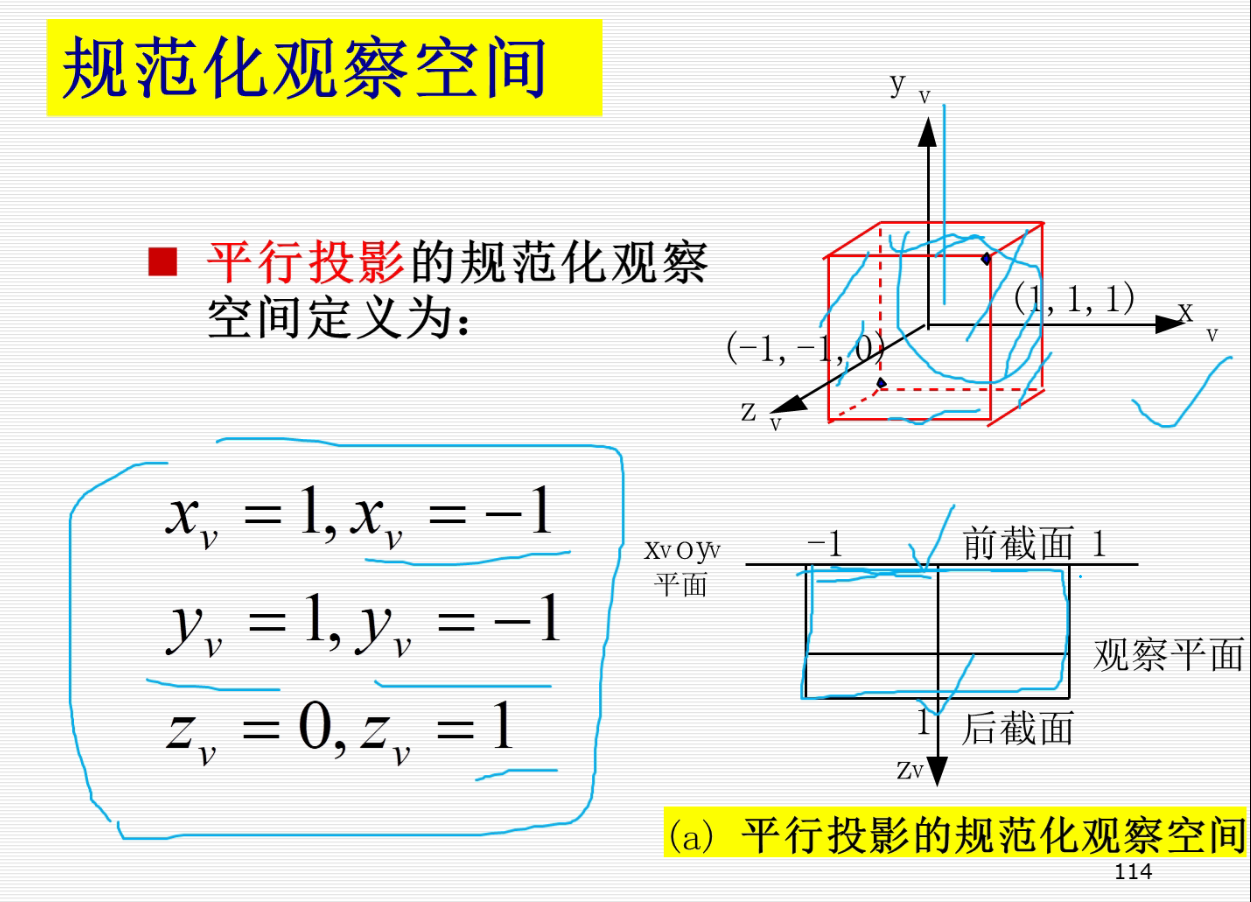
二维观察变换
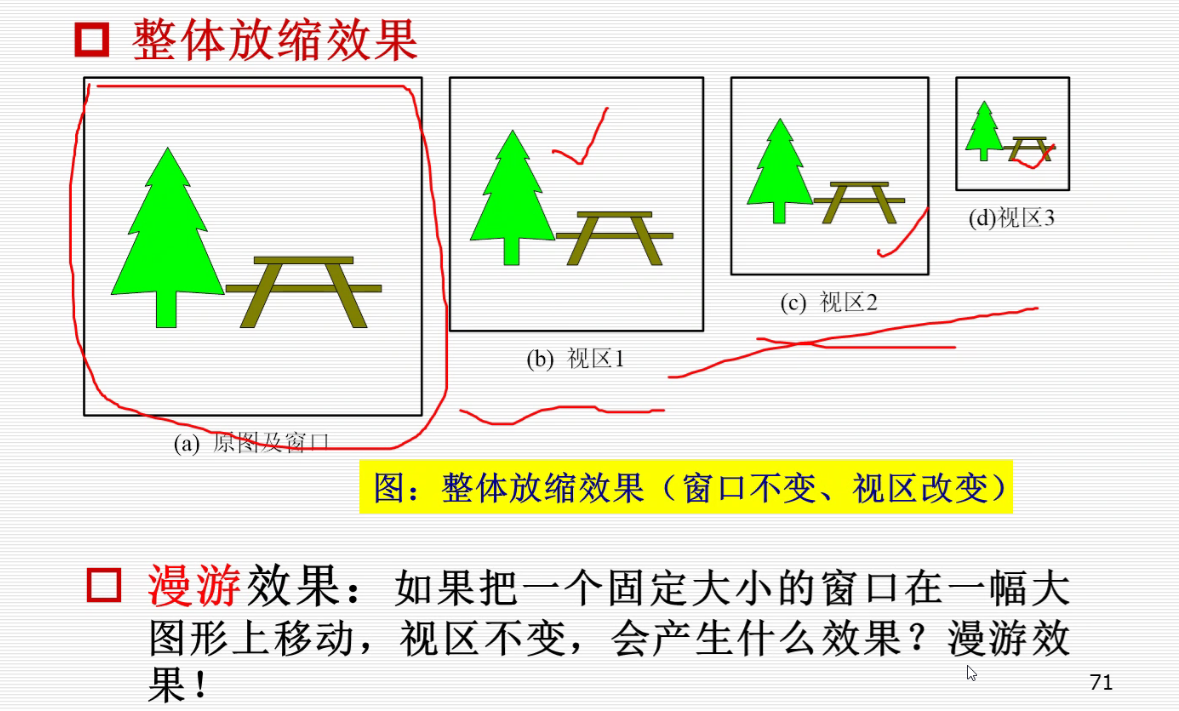
有关 窗口 的几个定义:用户域和窗口区
窗口用来定义下显示什么。比如框住一棵树,那么窗口就要显示树。

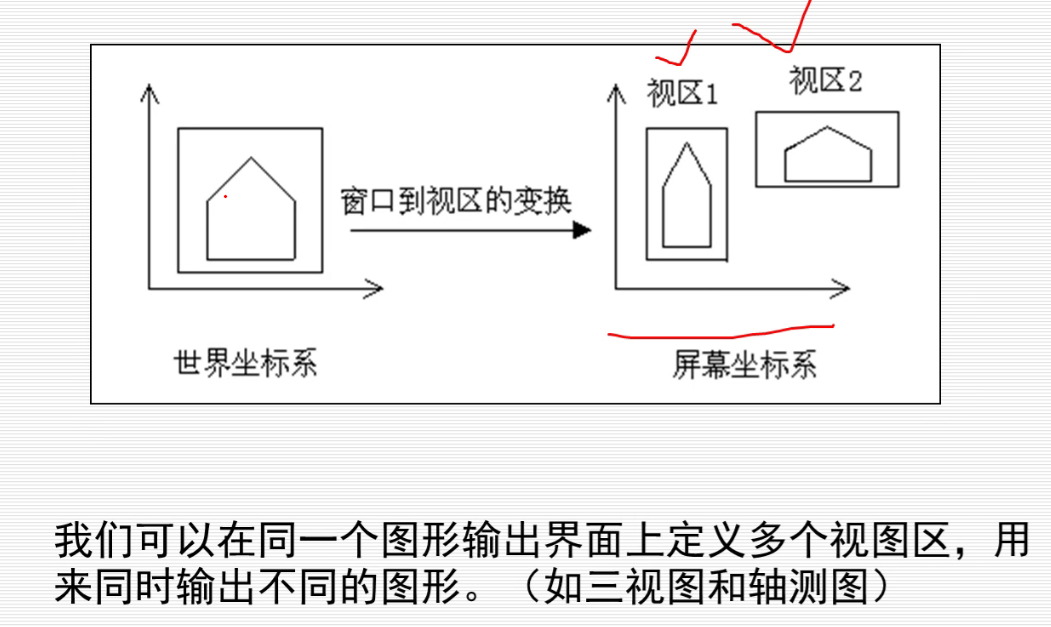
有关 视区 的几个定义:屏幕域和视图区
视区定义图象显示在何处,比如上面说到的那棵树在屏幕的哪儿就是视区定义的。

窗口和视图区

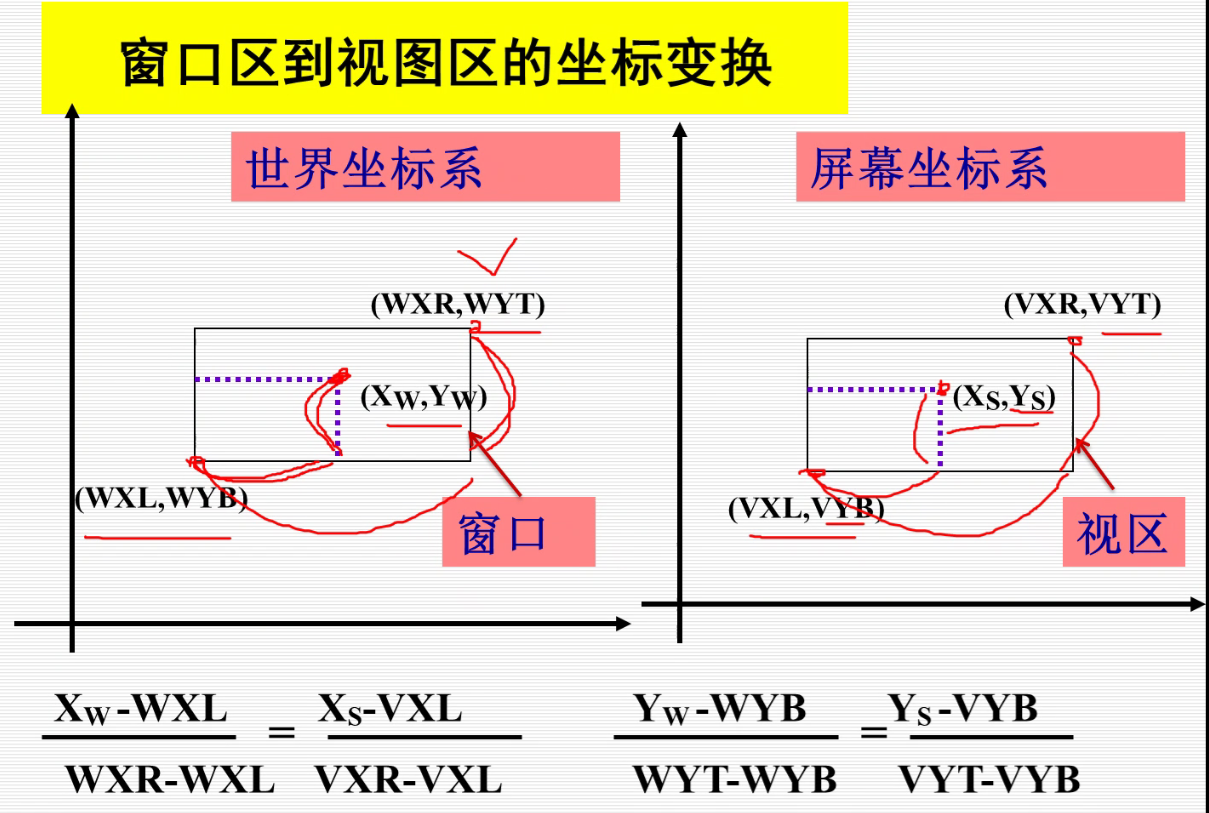
解得(这个解没必要背,理解上面两个公式,直接分别把$X_s,Y_s$移动到一边即可):
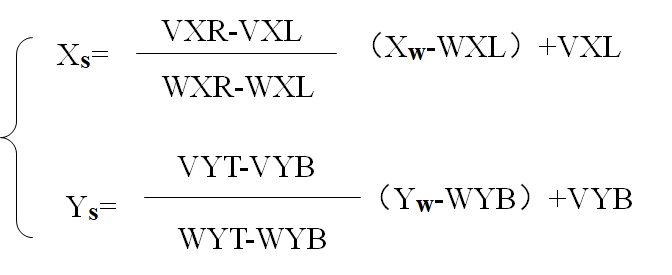
观察变换
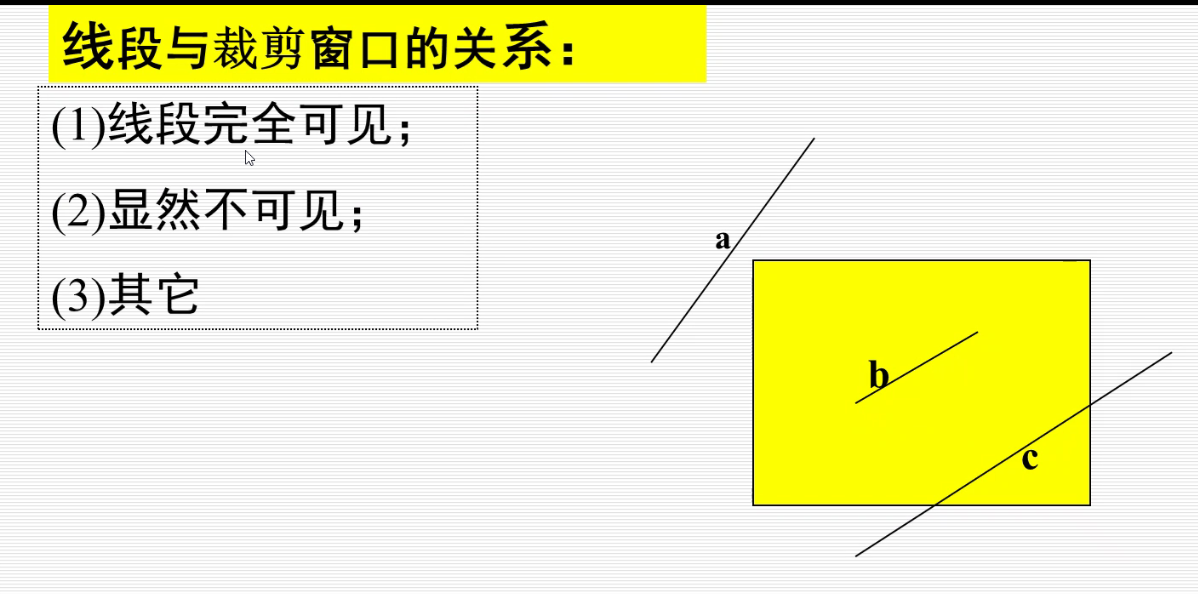
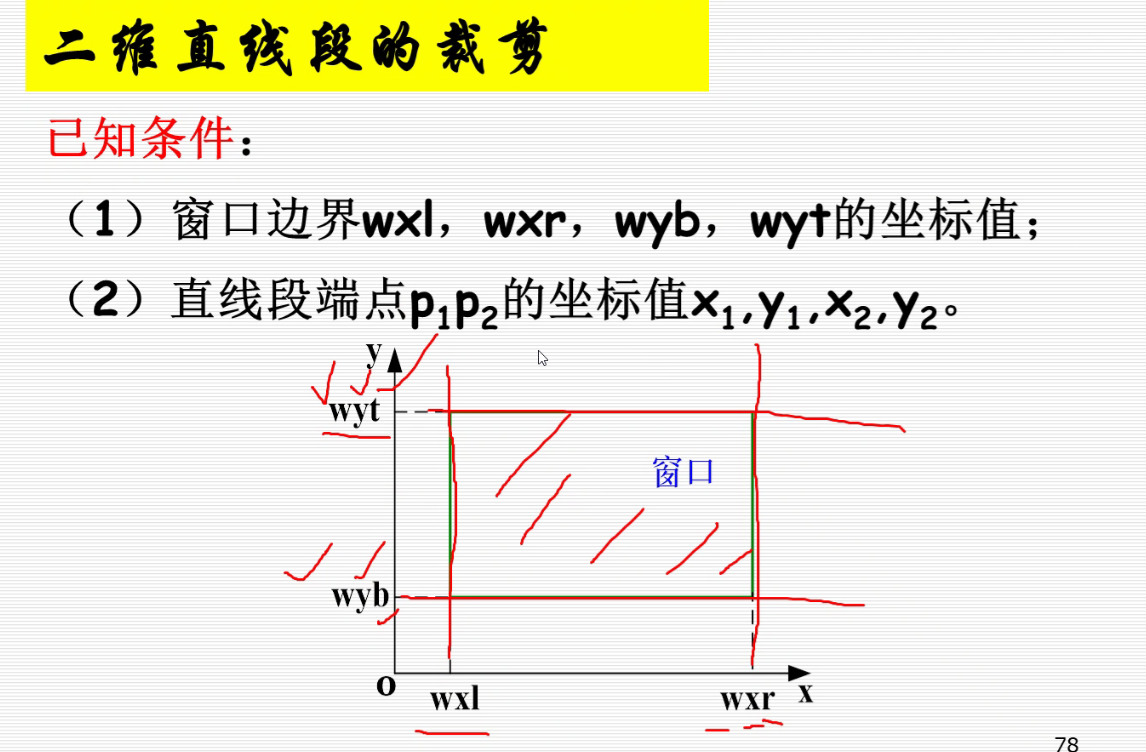
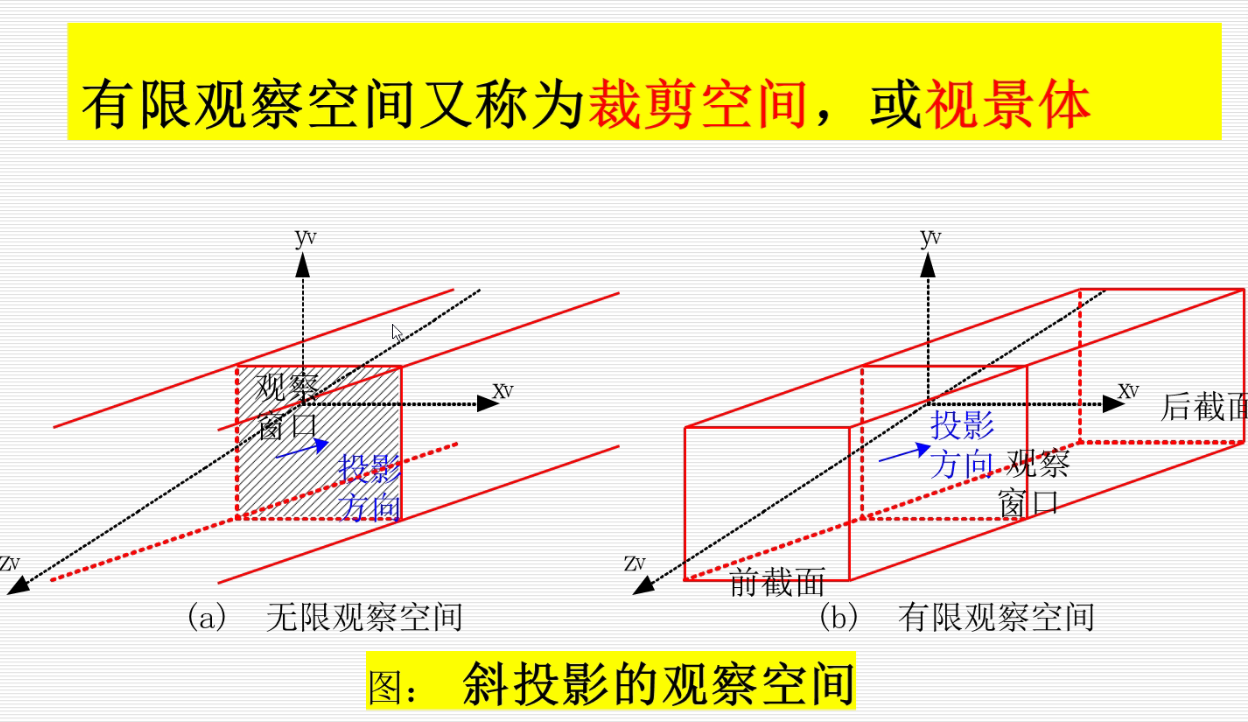
裁剪


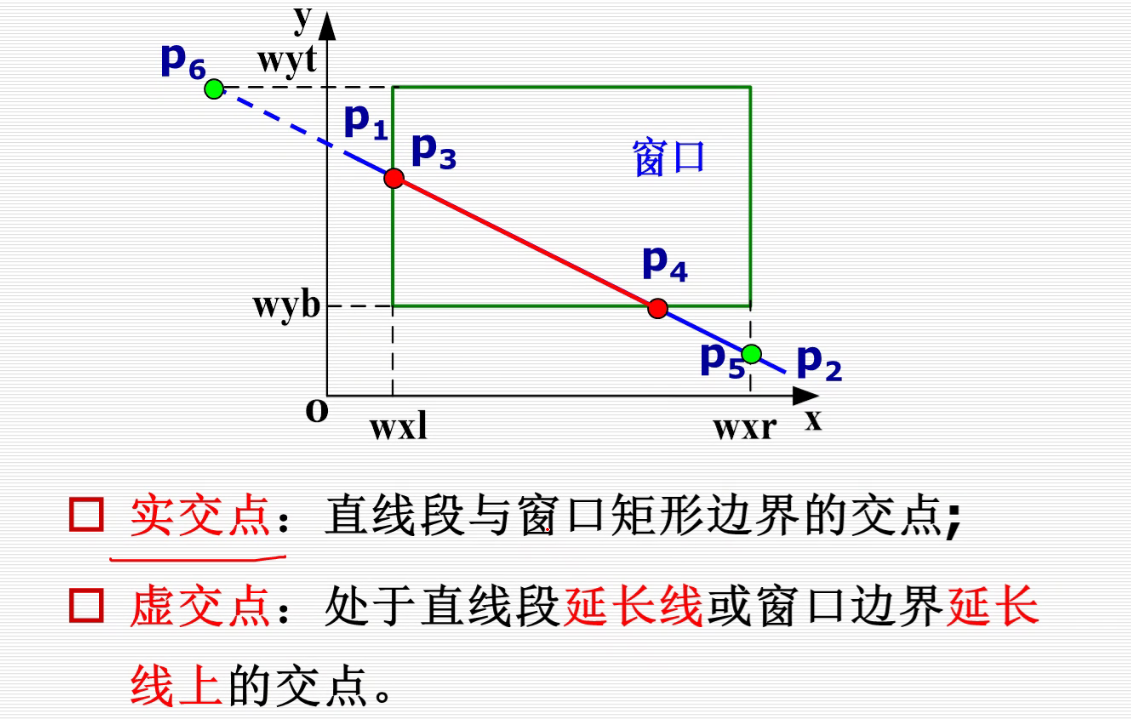
Cihen-Sutherland裁剪算法

落在窗口内就是0000.
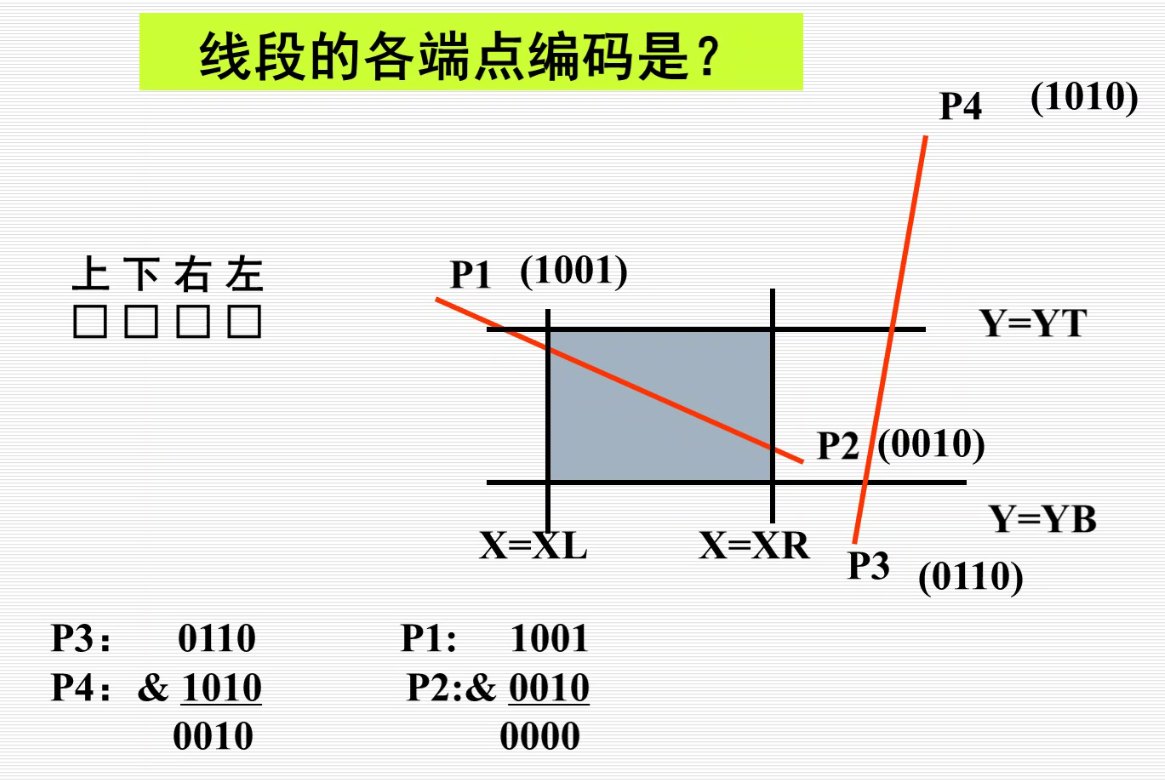
如果是立方体:那么需要6位编码(立方体六个面)
具体算法:https://blog.csdn.net/soulmeetliang/article/details/79179350

用Cohen-Sutherland编码最多求4次交点。
中点分割算法(对分法)
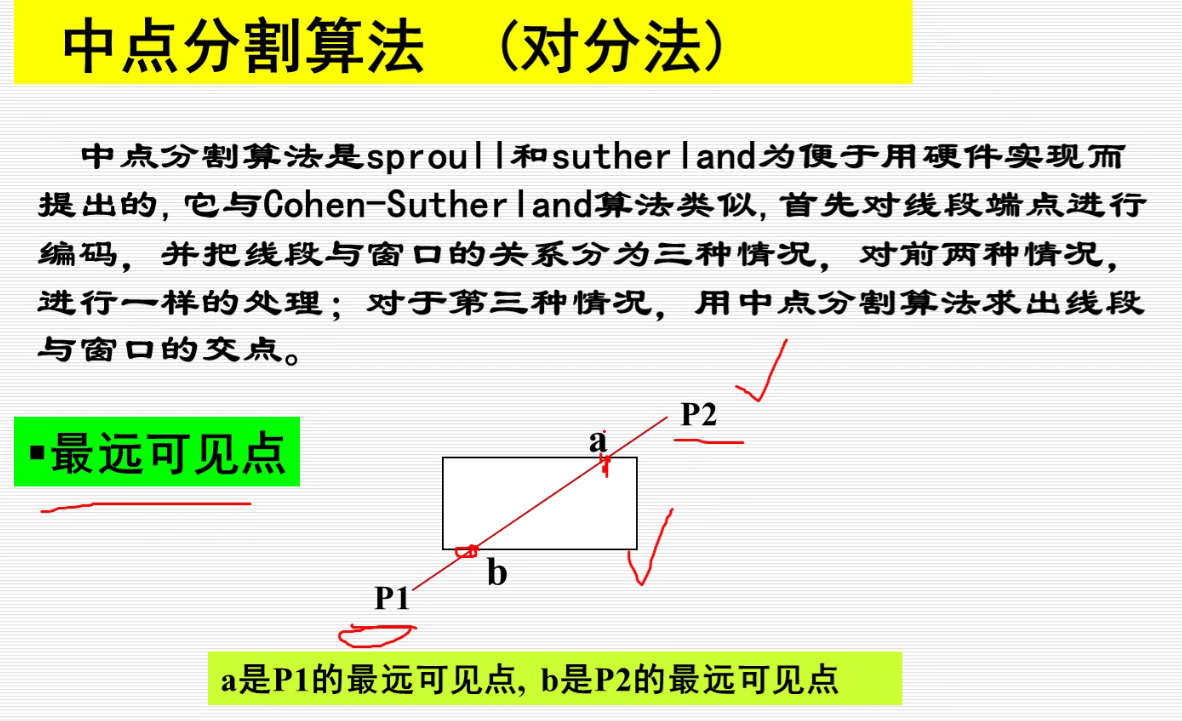

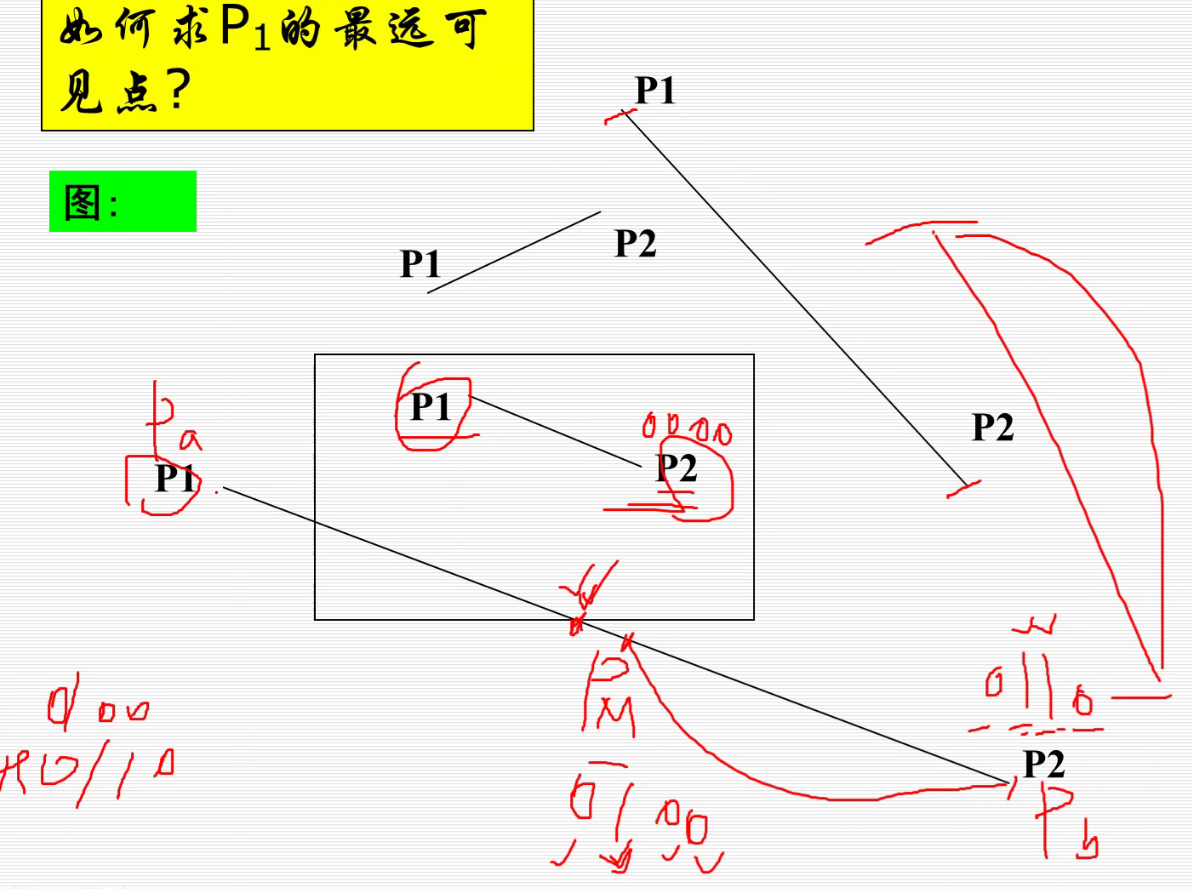
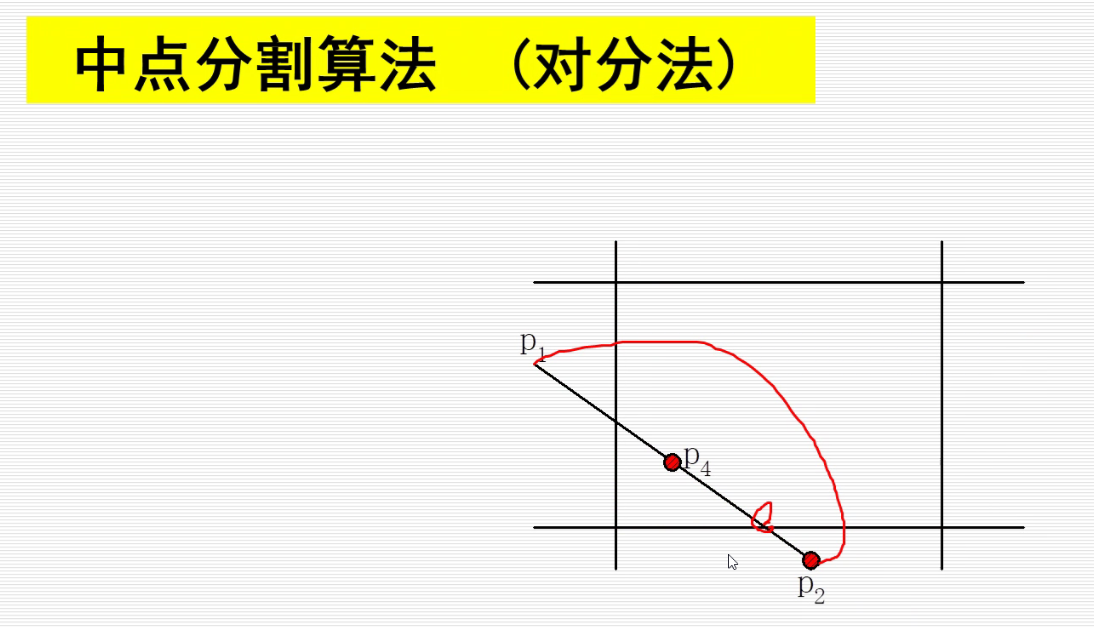
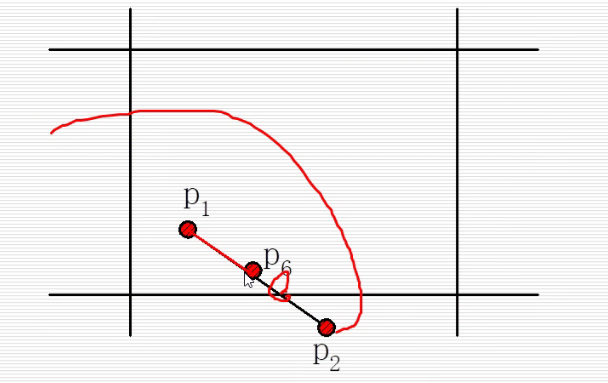
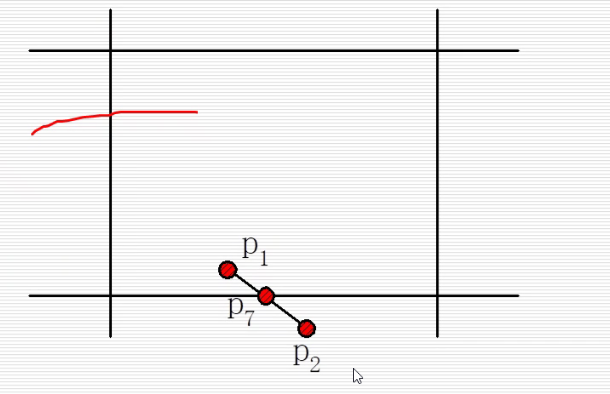

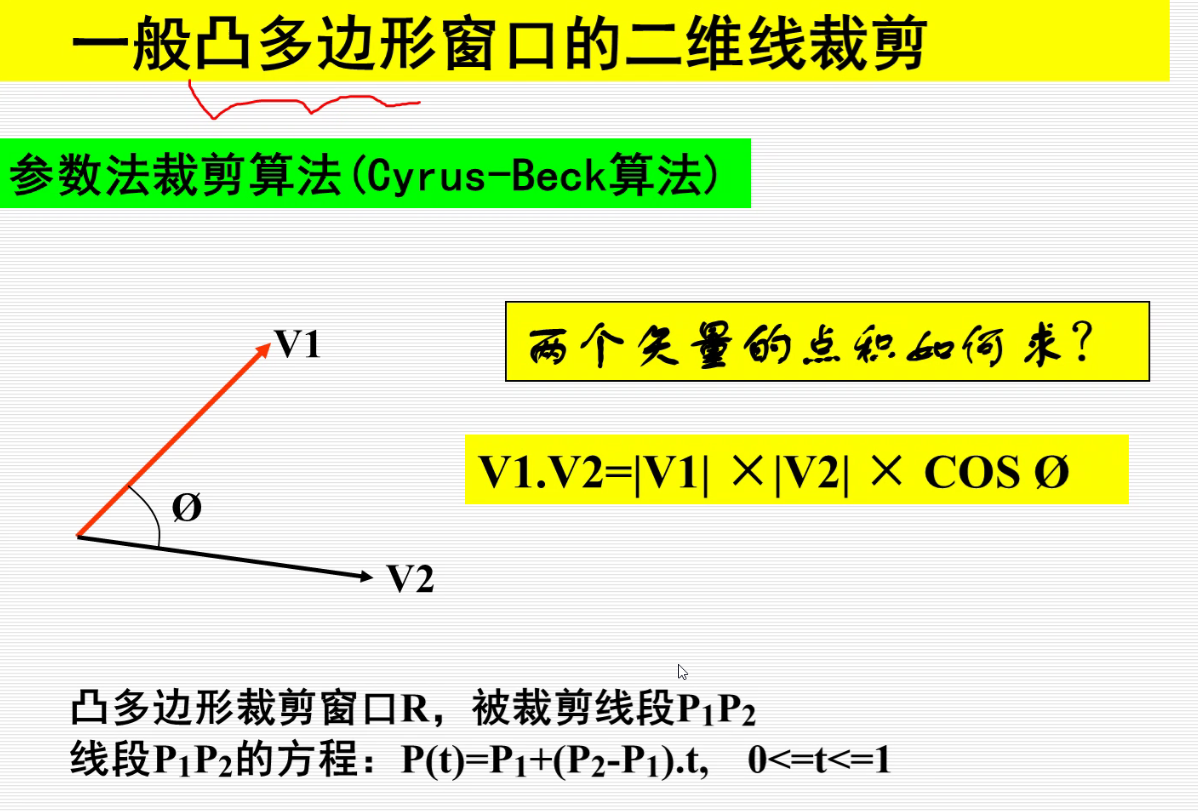
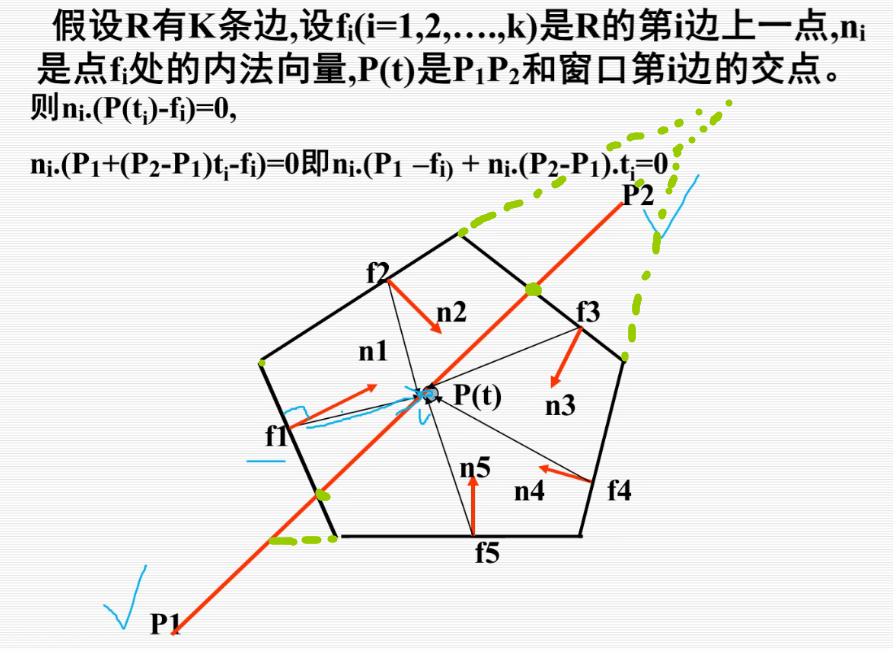
参数裁剪算法(Cyrus-Beck)
下面的两个交点和P1一共3个点 要求最大值,上面的 三个点和P2一共四个点 求最小值,即可求出相交线段。可是如何知道哪个点算作上部分,哪个点算作下部分呢?我们先看边的法向量和向量P1P2的夹角,如果夹角小于90,算下部分;大于90算上部分。

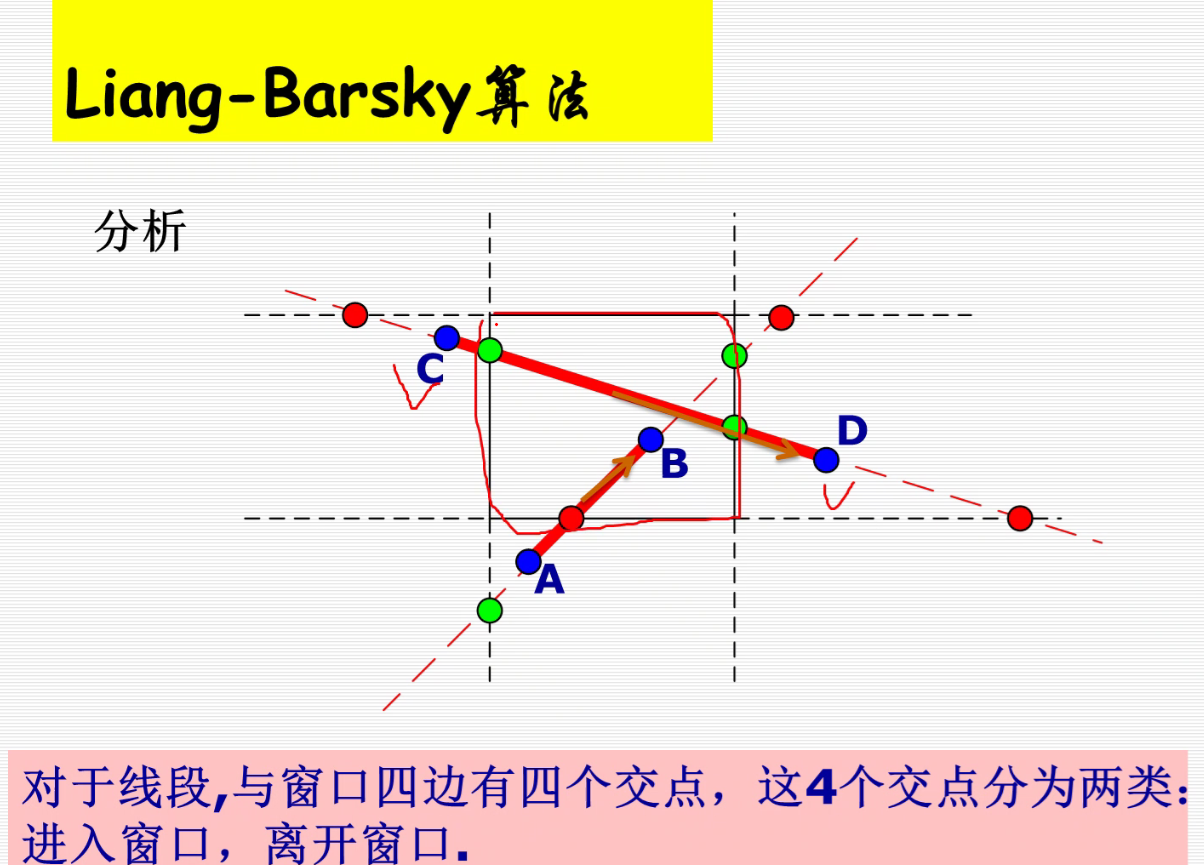
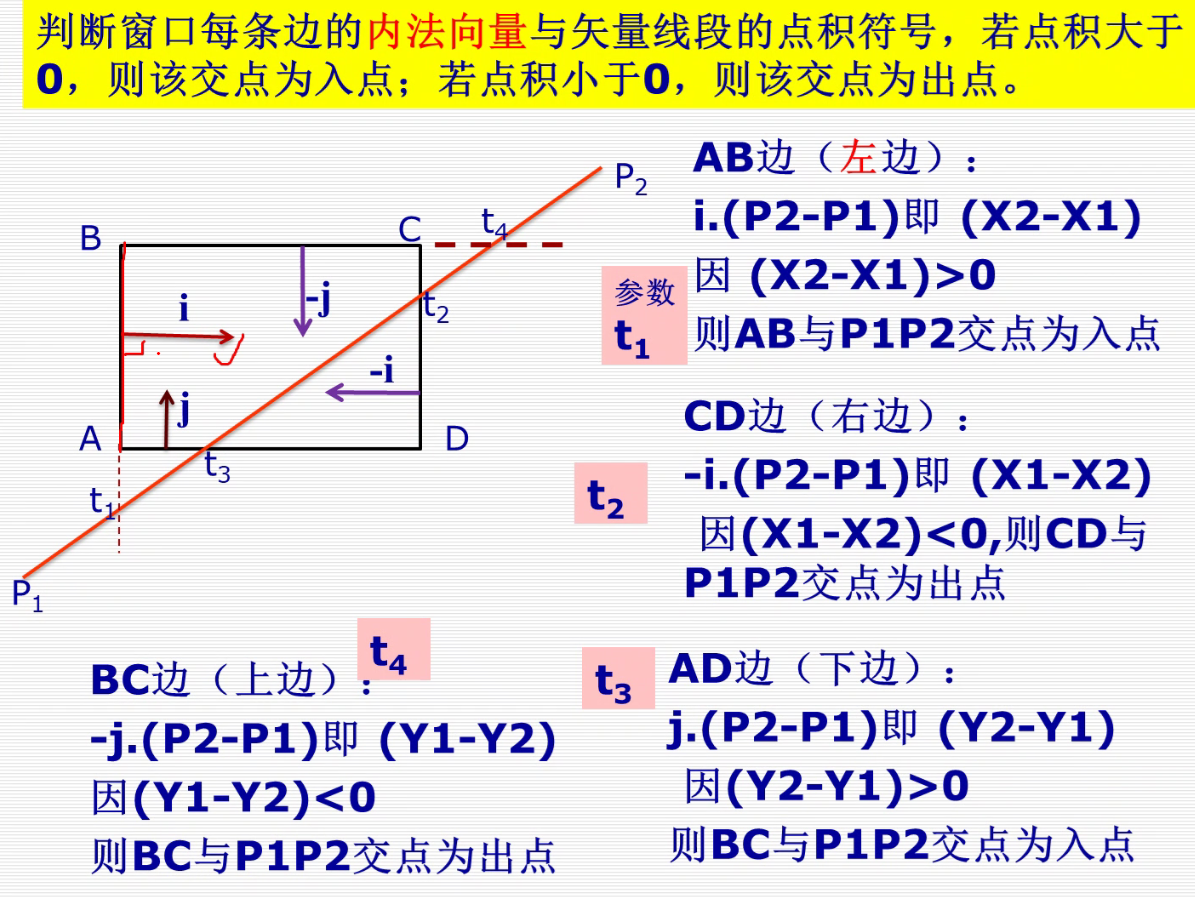
Liang-Barsky算法
详细介绍:https://blog.csdn.net/keneyr/article/details/83871170
https://blog.csdn.net/soulmeetliang/article/details/79185603



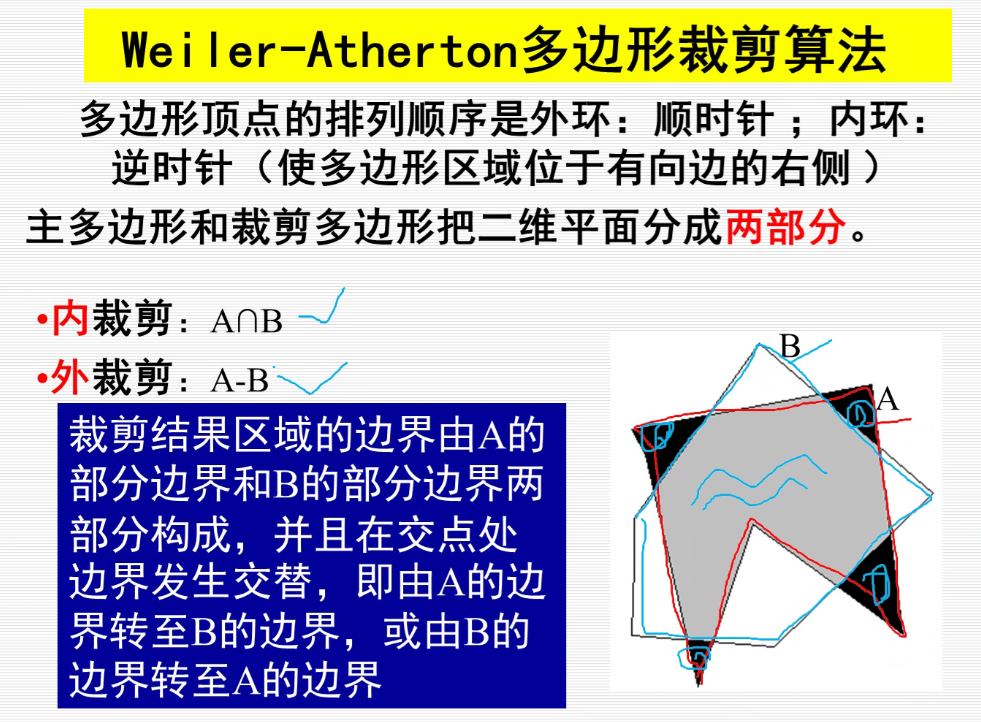
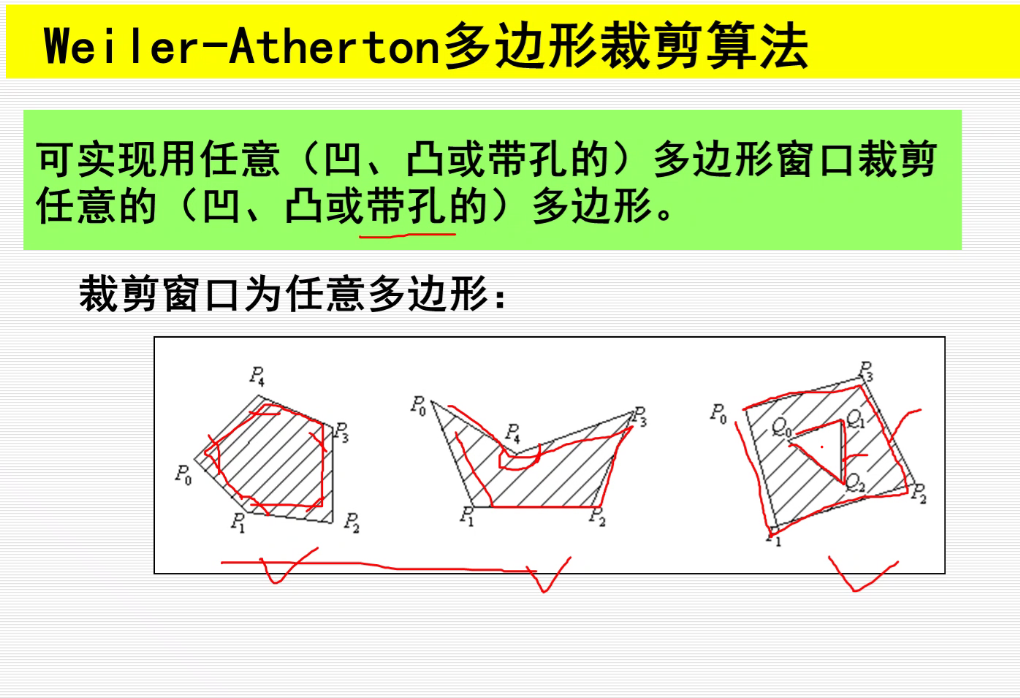
Weiler-Atherton多边形裁剪算法:
https://blog.csdn.net/yangxi_pekin/article/details/37738219
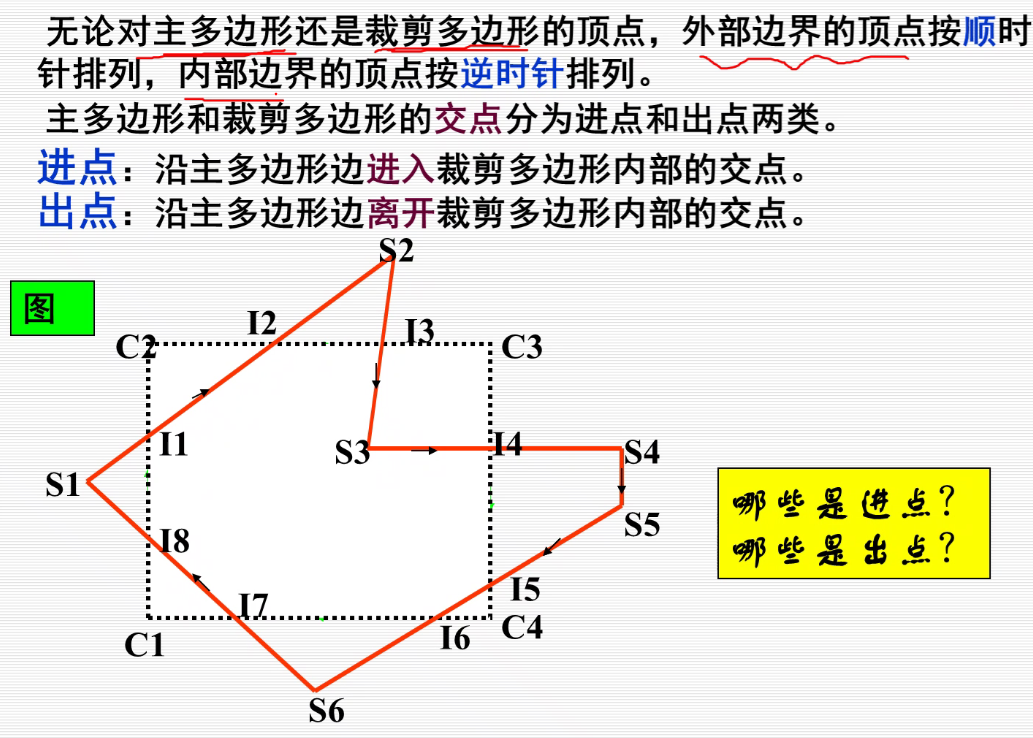
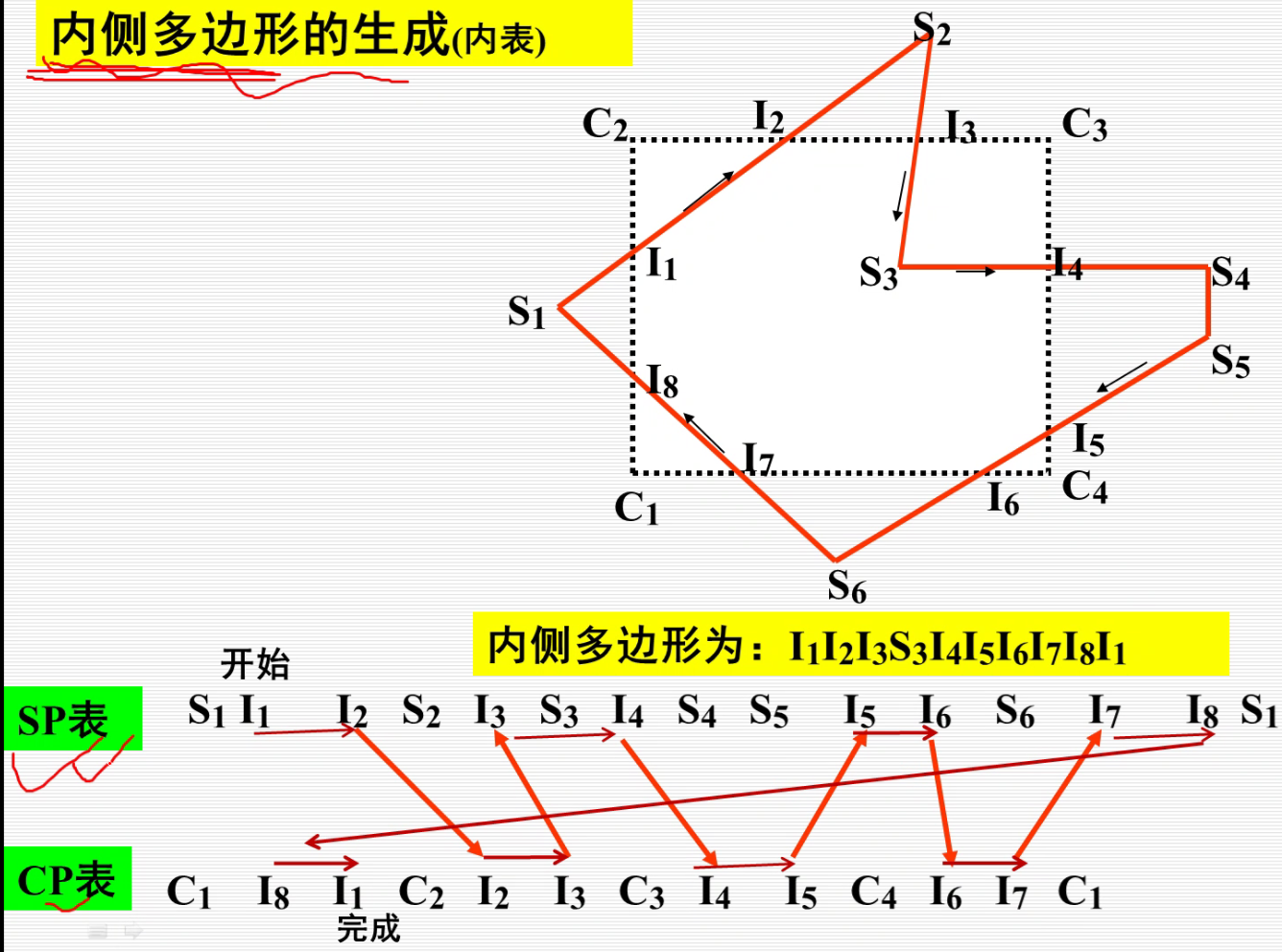
$I_1,I_3,I_5,I_7$是进点
内裁剪:
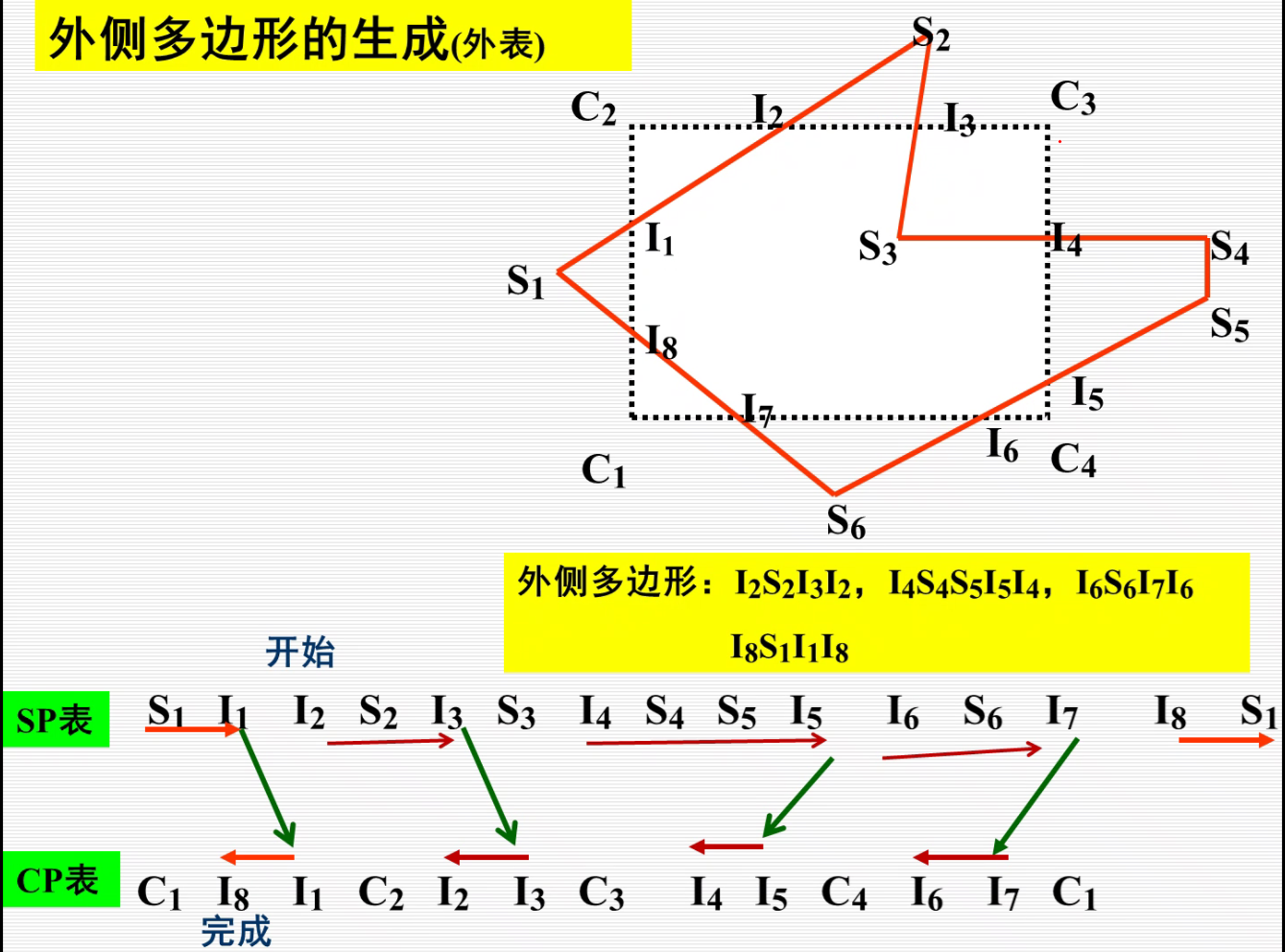
外裁剪:
Sutherland-Hodgeman多边形裁剪
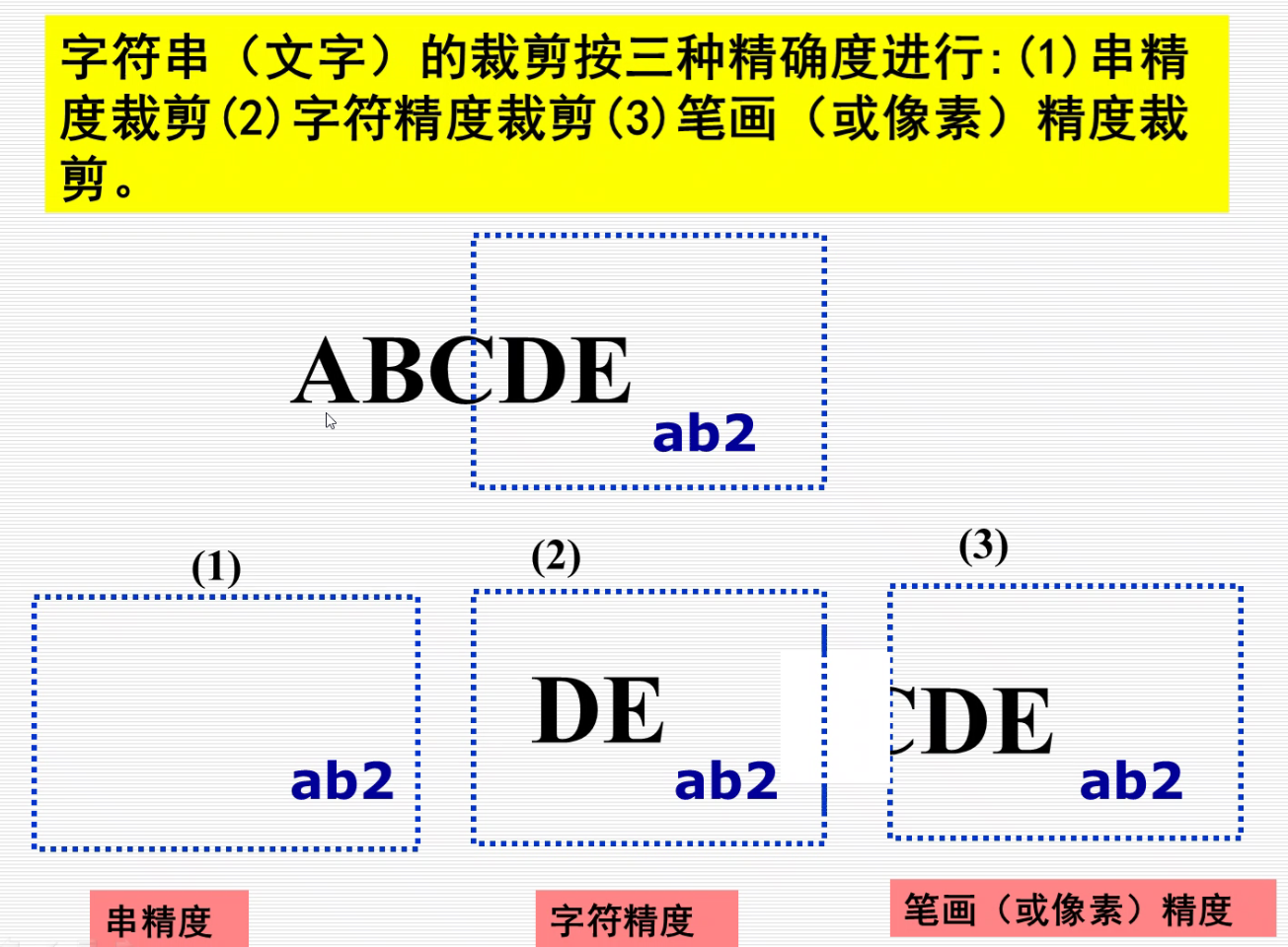
字符裁剪
第七章:三维变换及三维观察
三维上 的裁剪
三维上的几何变换
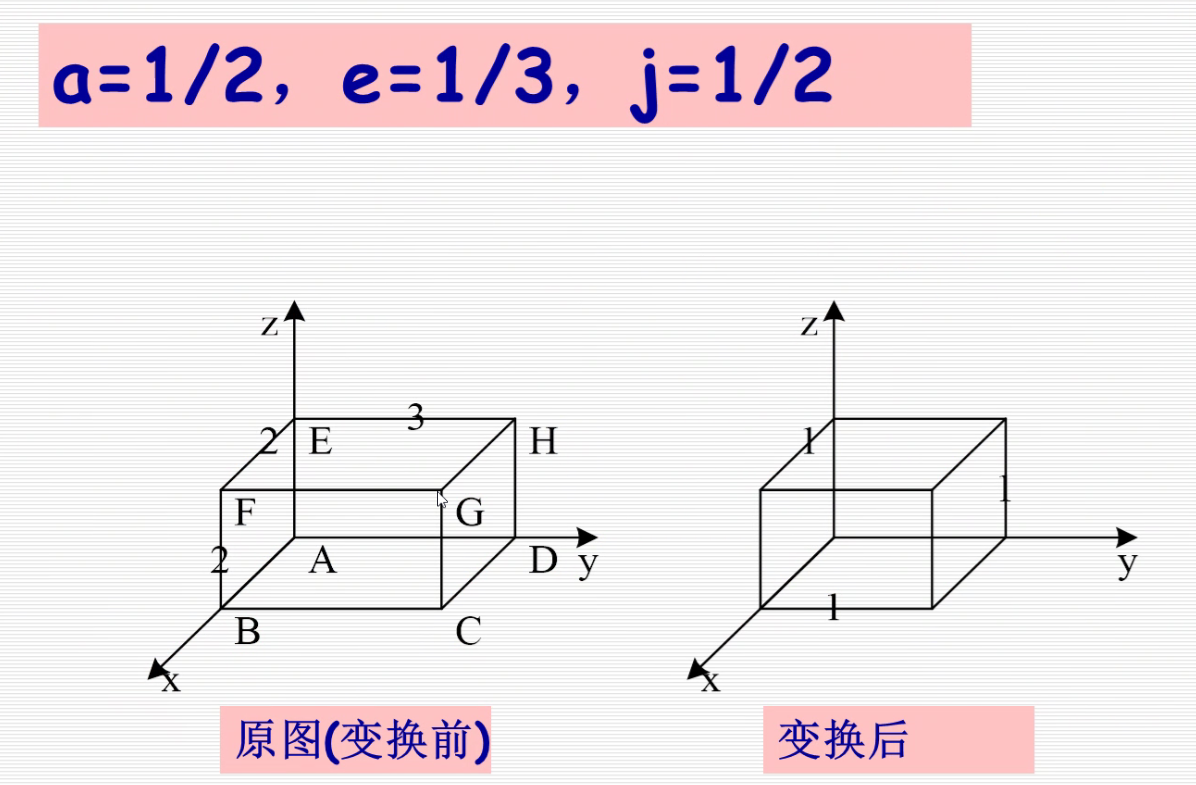
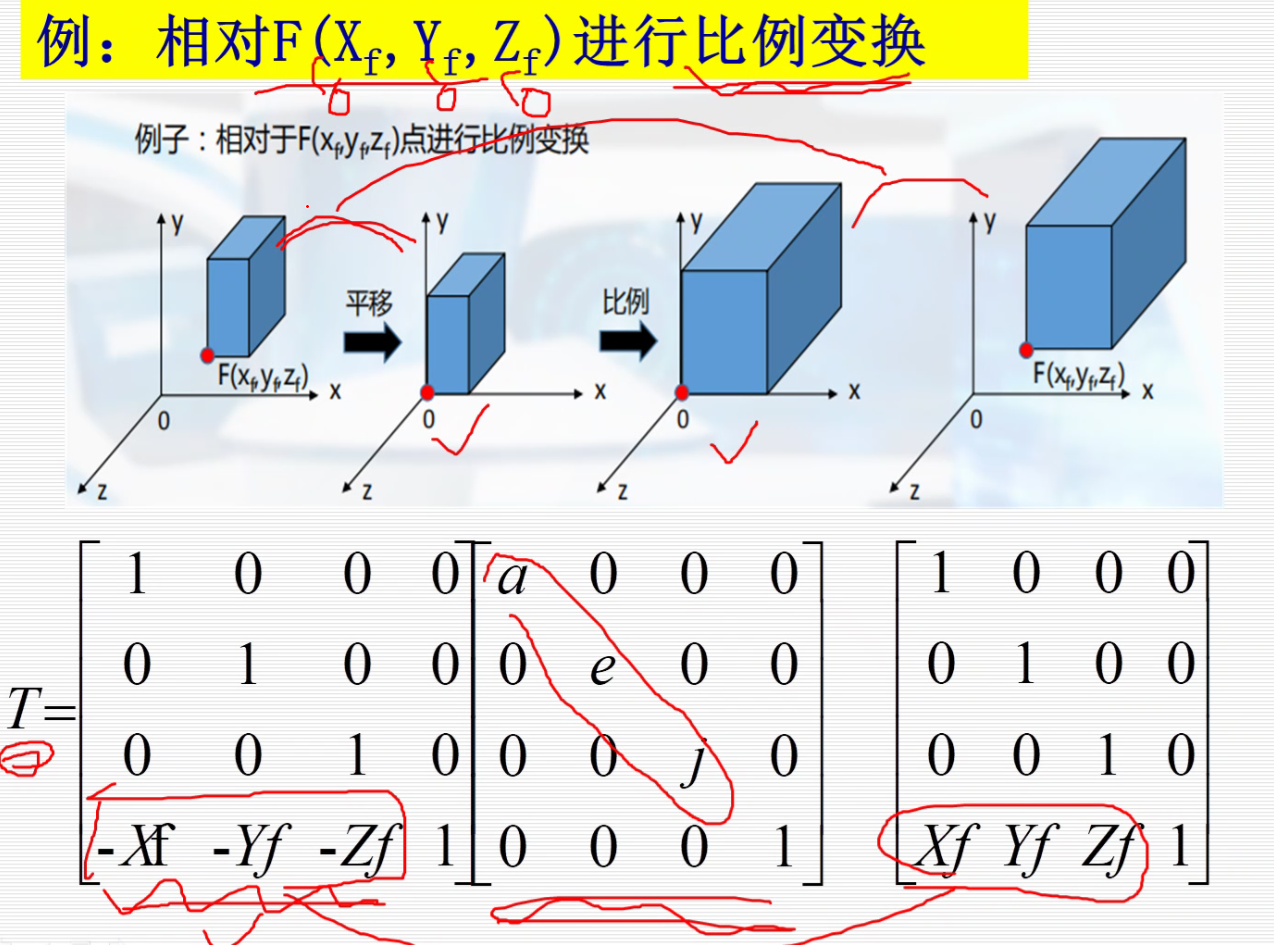
比例变换
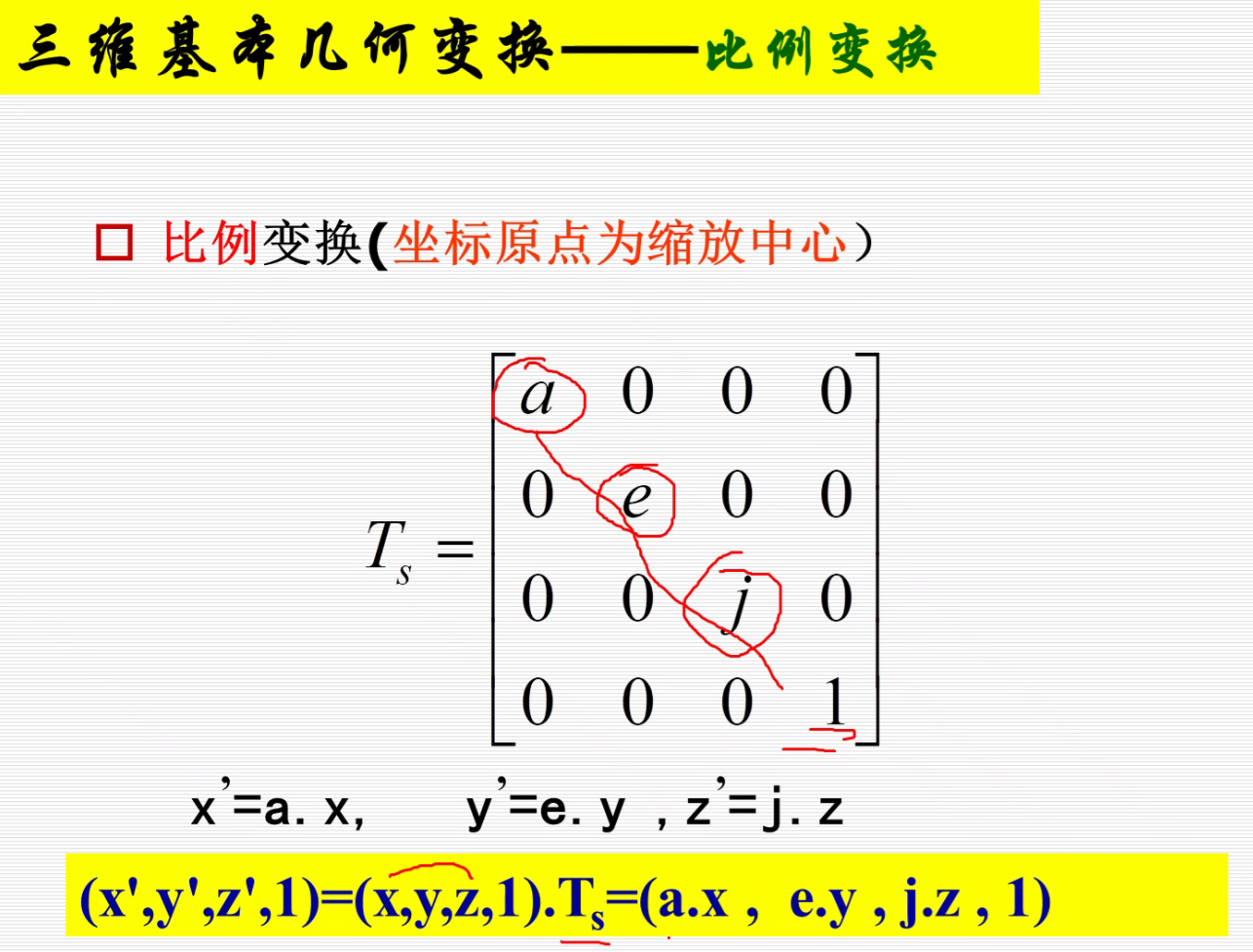
逆变换:a,e,j变为原来的倒数
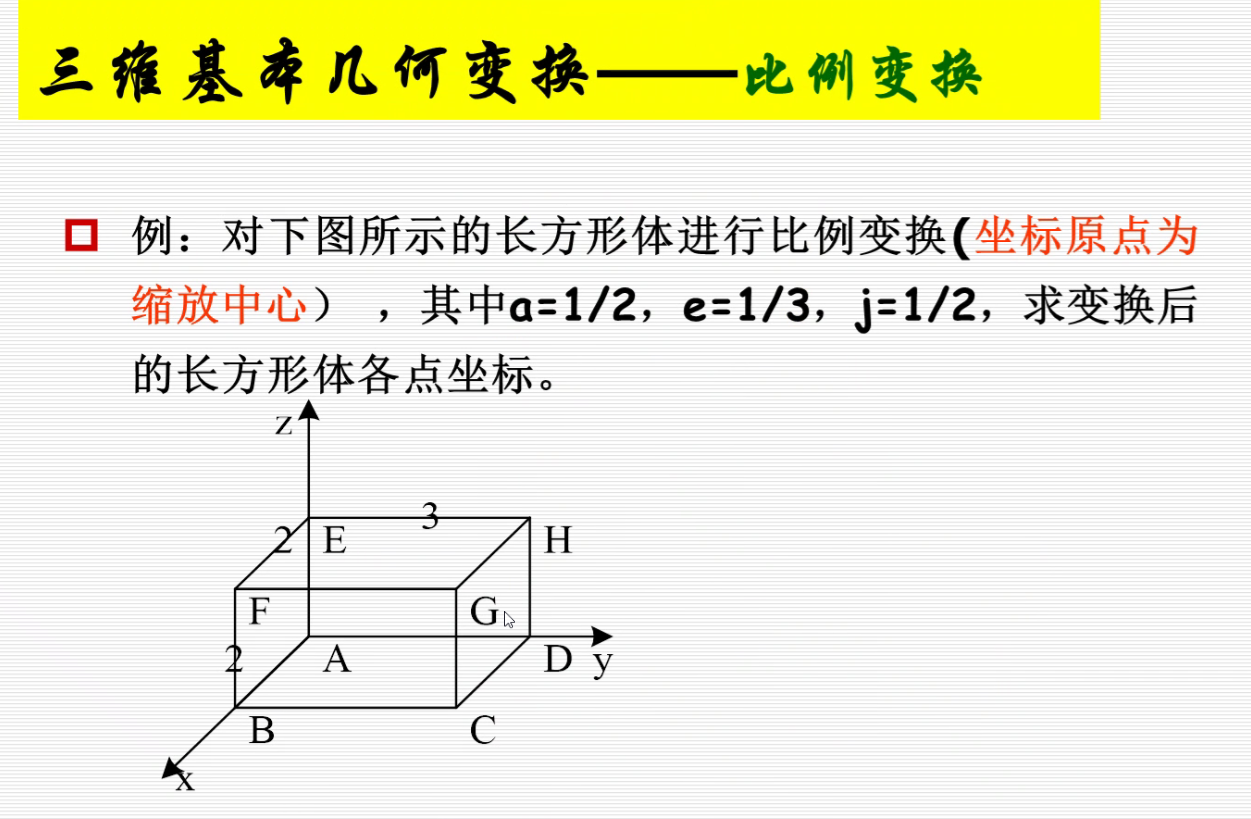
解:

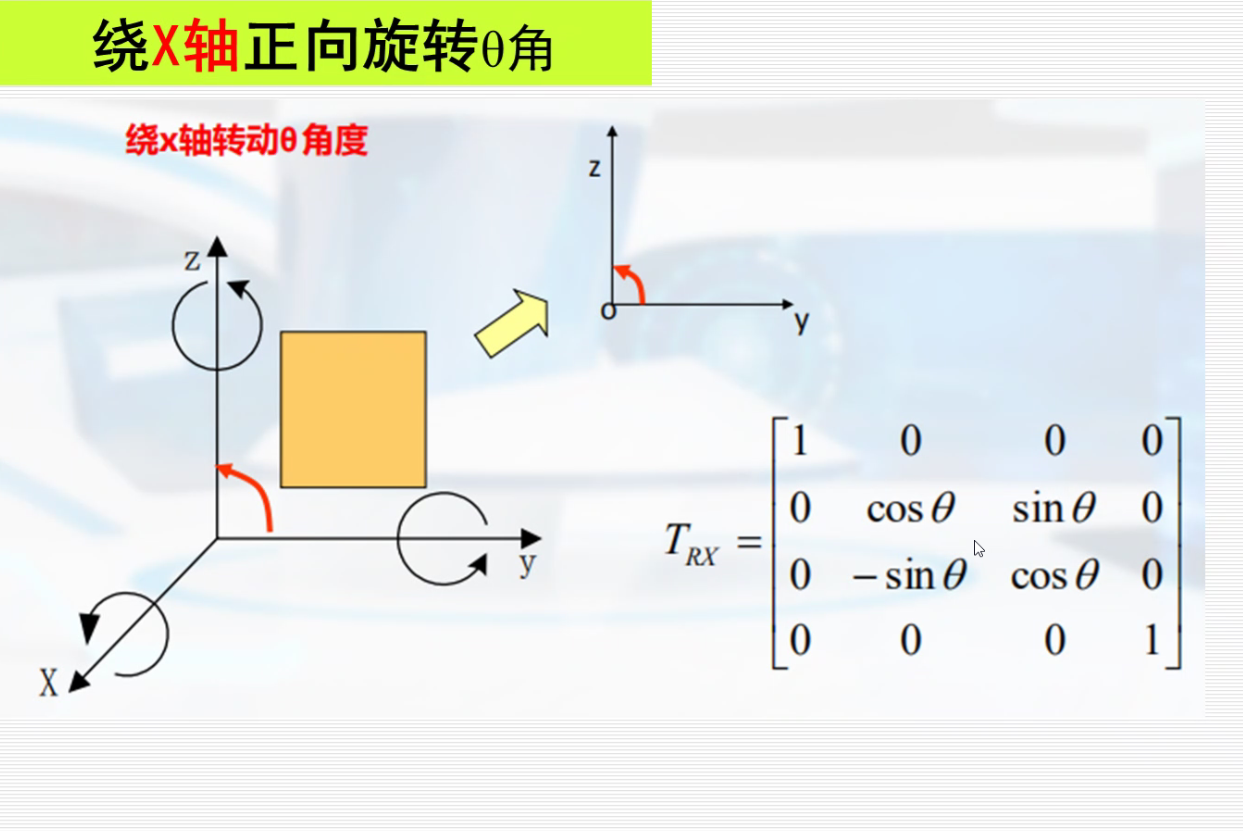
旋转变换:
规定用右手坐标系
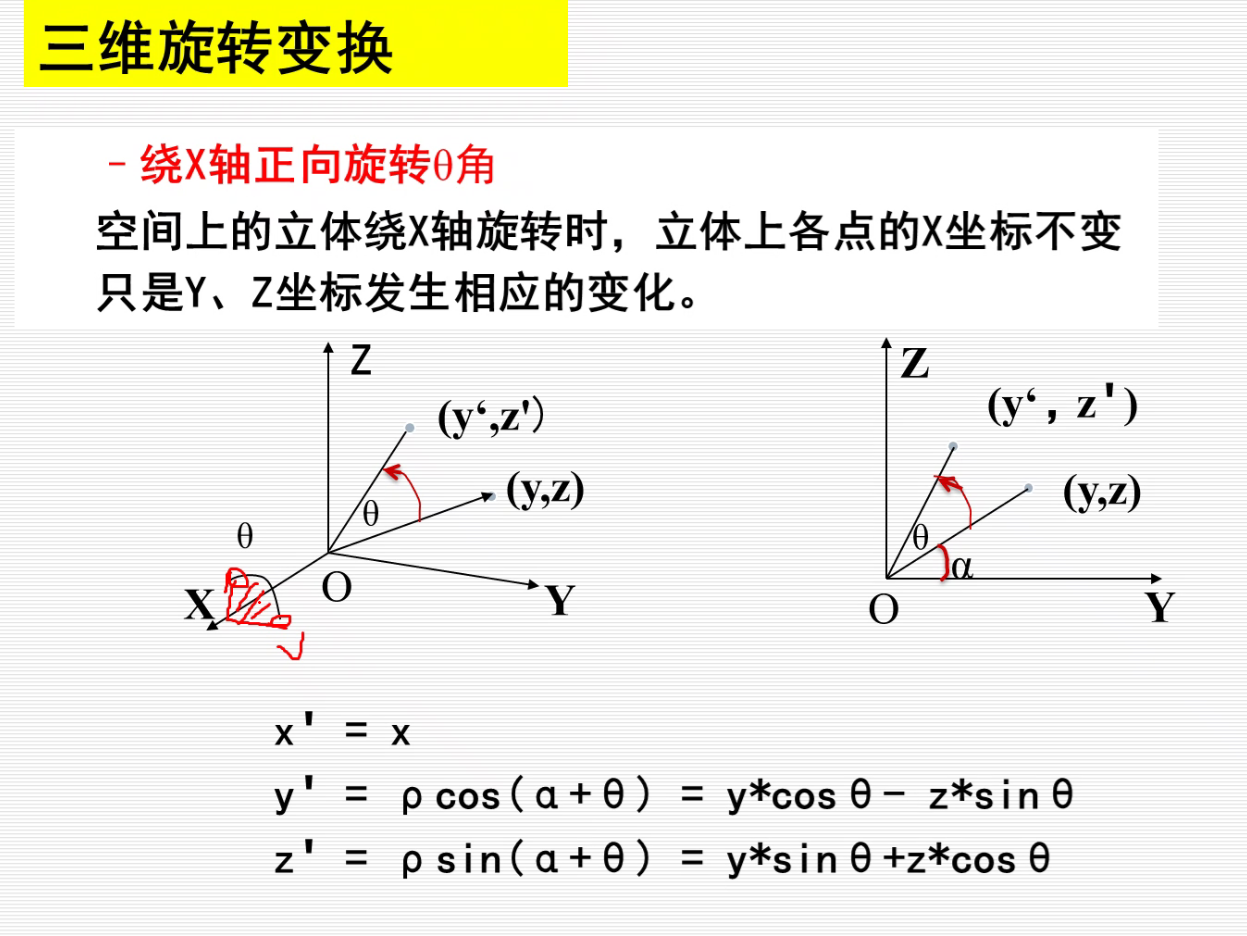
按照X’ Y’ Z’的顺序对应着找,就可以写出下面的旋转矩阵,不用死记。
$[X’,Y’,Z’,1] ·T_{RX}=[x,ycosθ-zsinθ,ysinθ+zcosθ]$
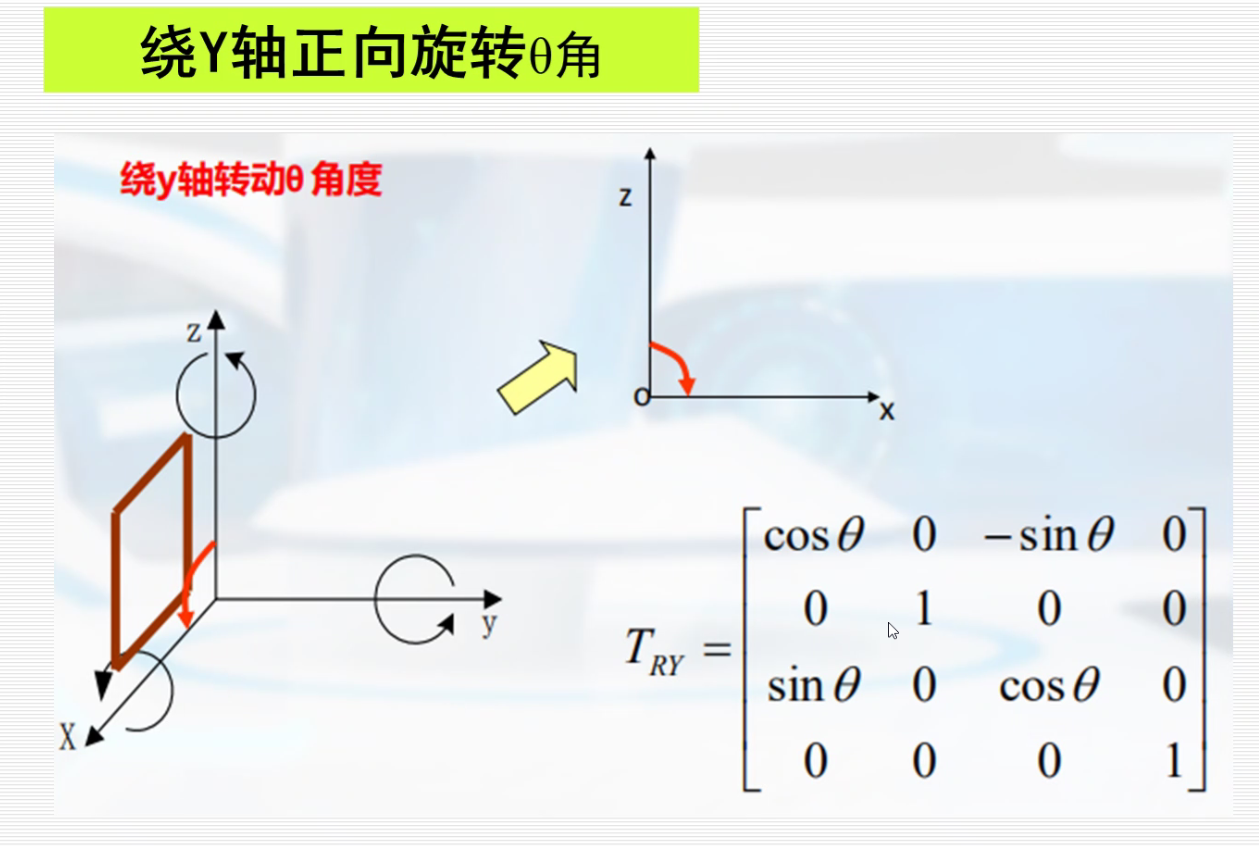
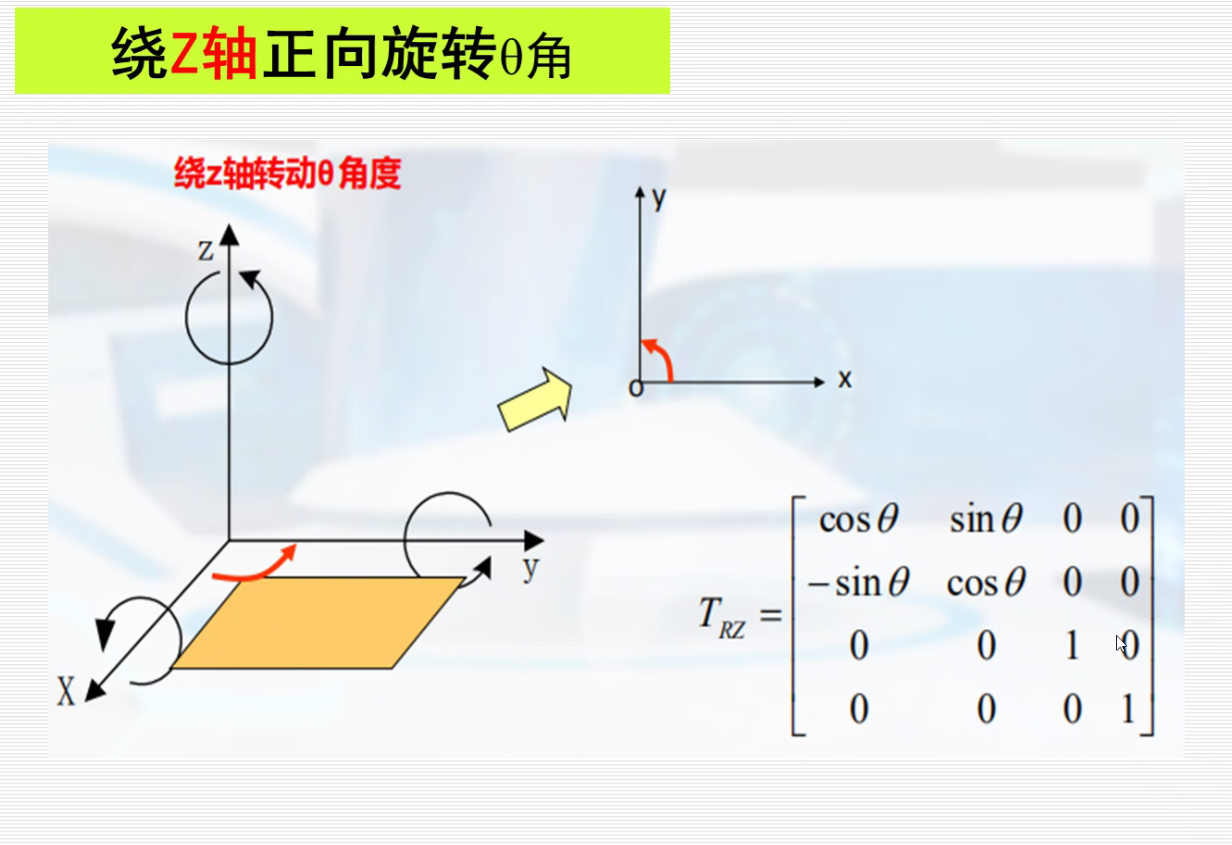
对称变换:

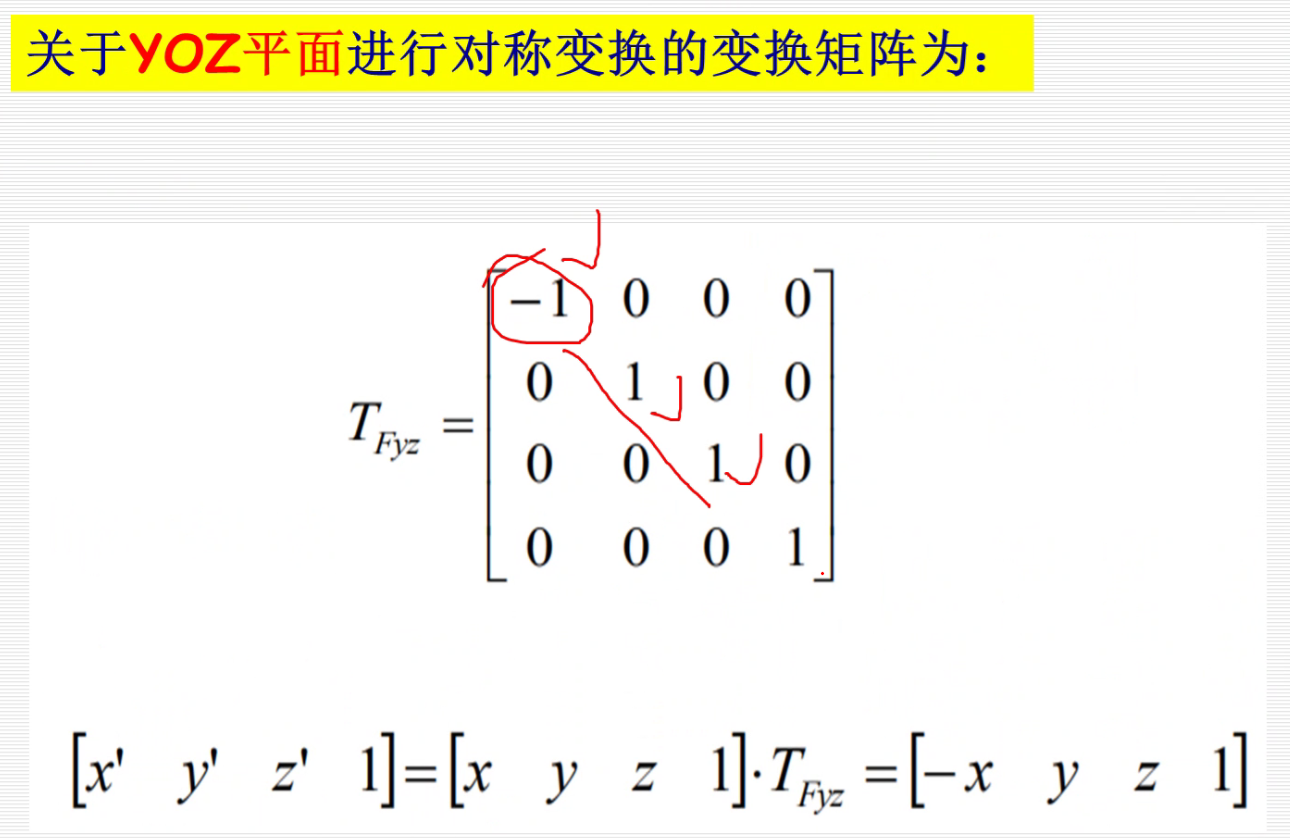

关于平面的变换和比例变换一个道理,相当于变成原来的-1倍


错切变换:
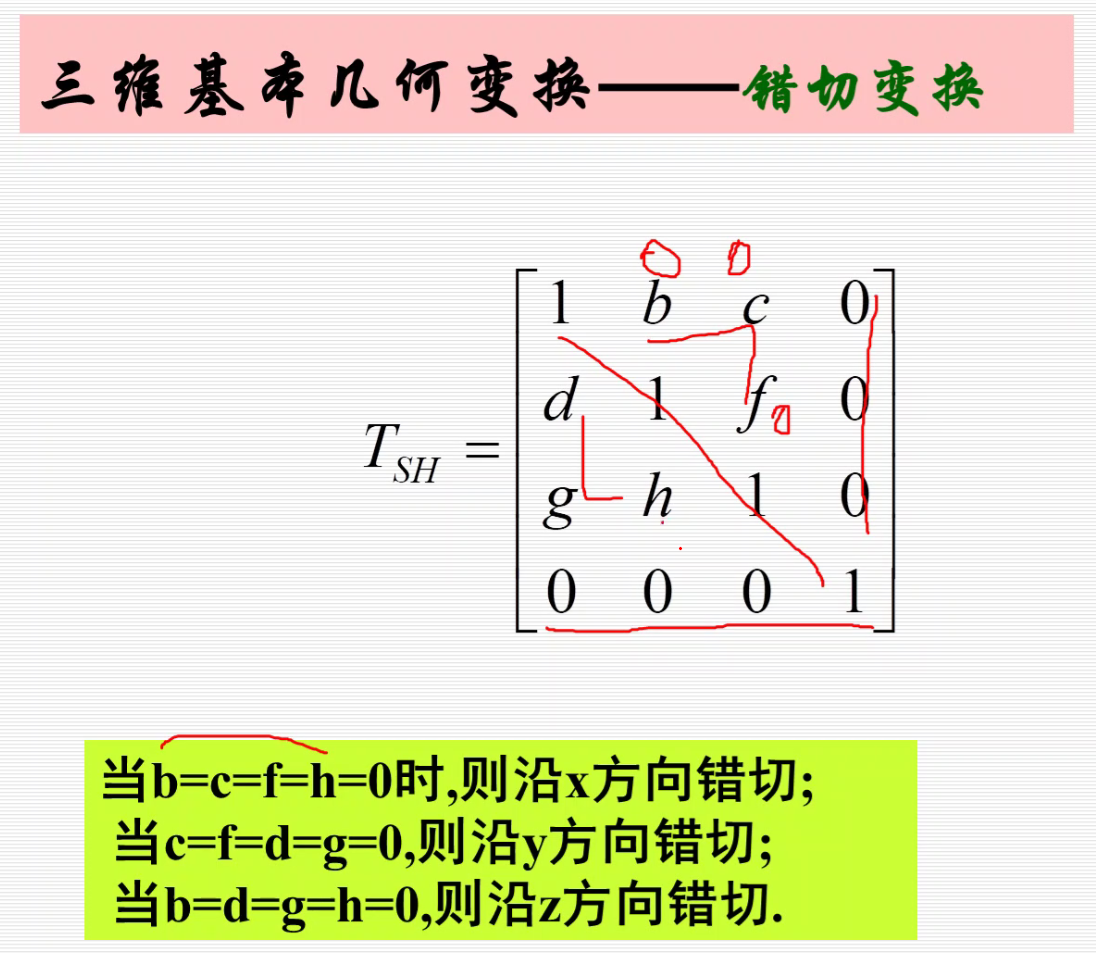
c=f=0时,不难看出z’=z 。b=0,h=0则y’=y 。x’=x+dy+gz。
后面两个同理。
平移变换:
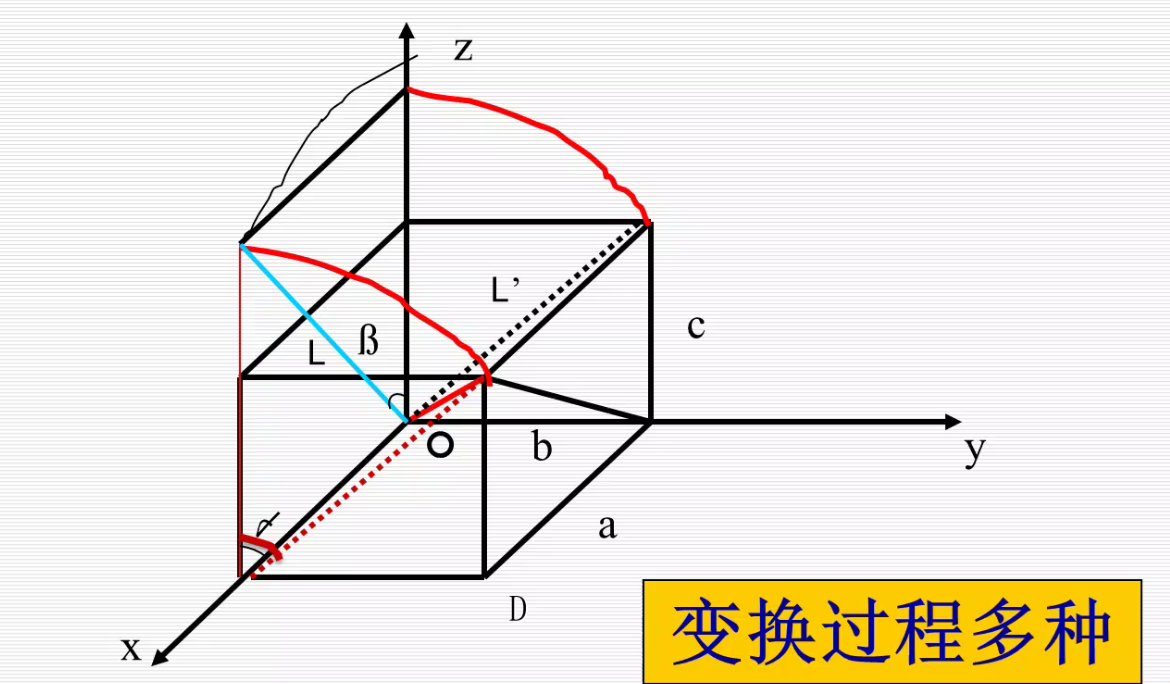
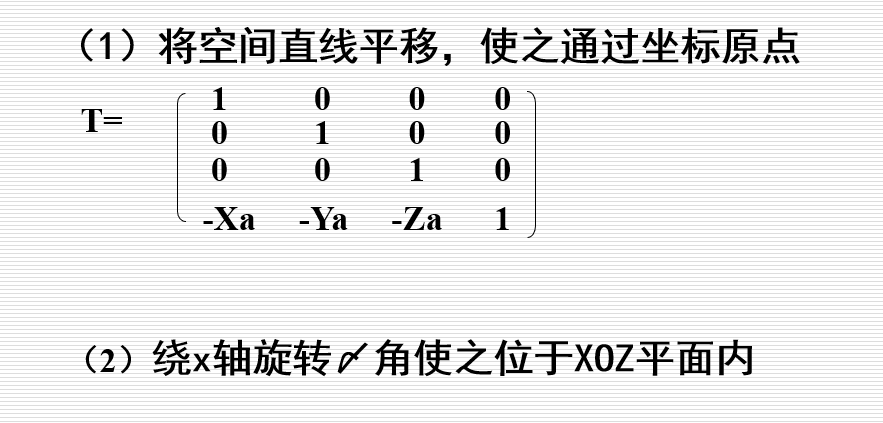
绕空间轴三维旋转变换:



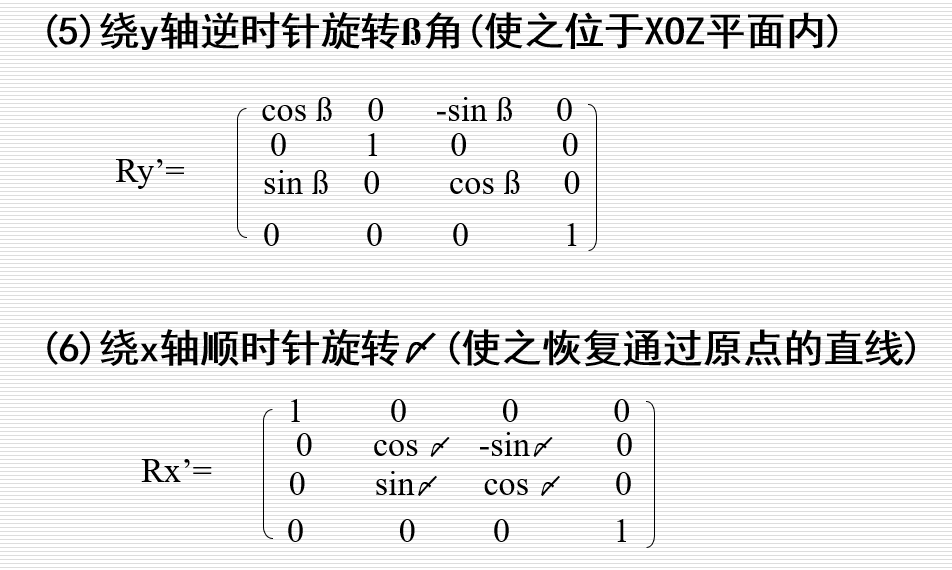

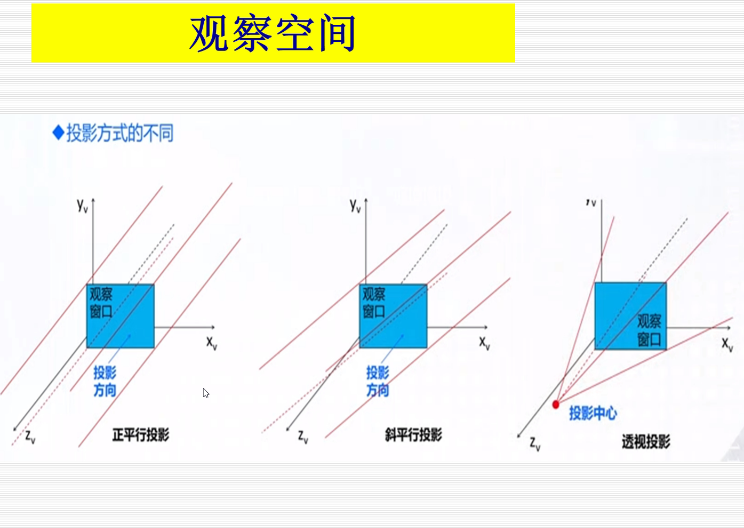
三维上的投影

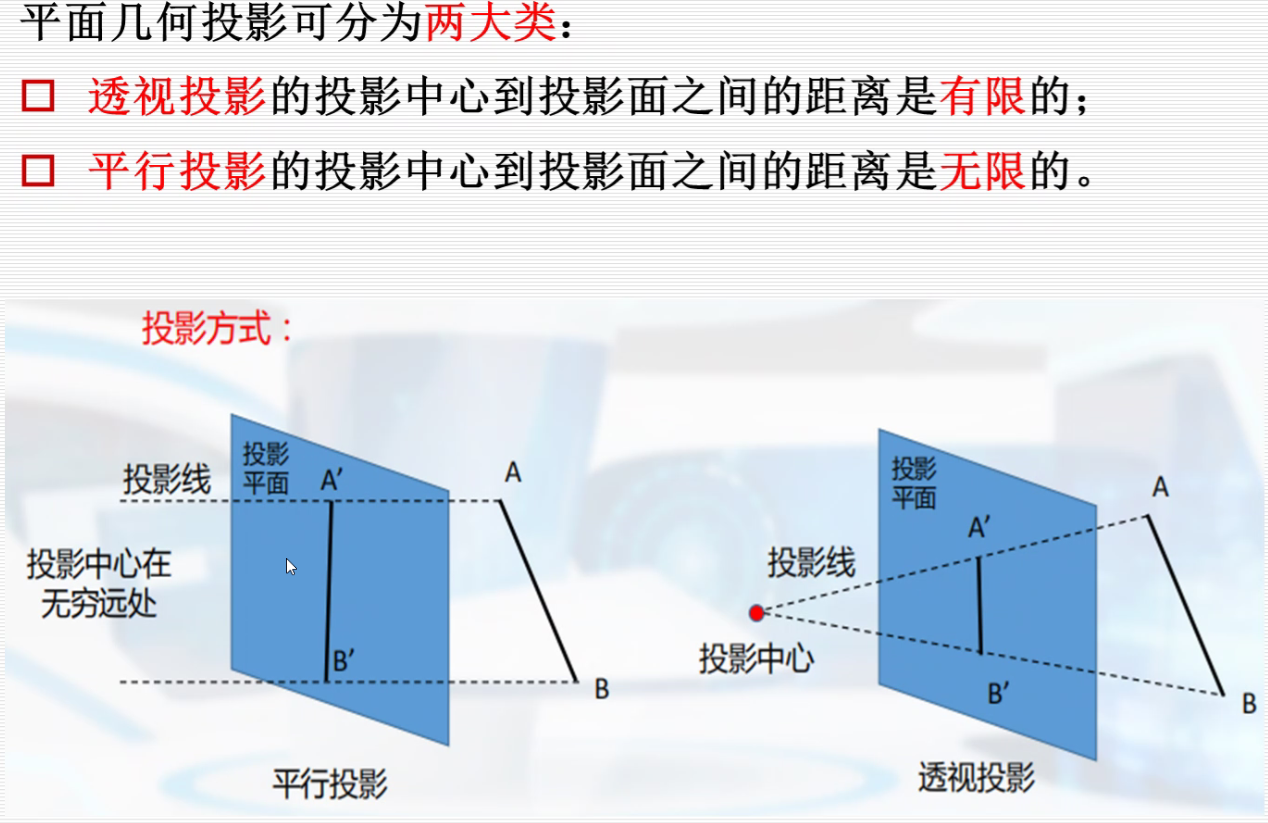
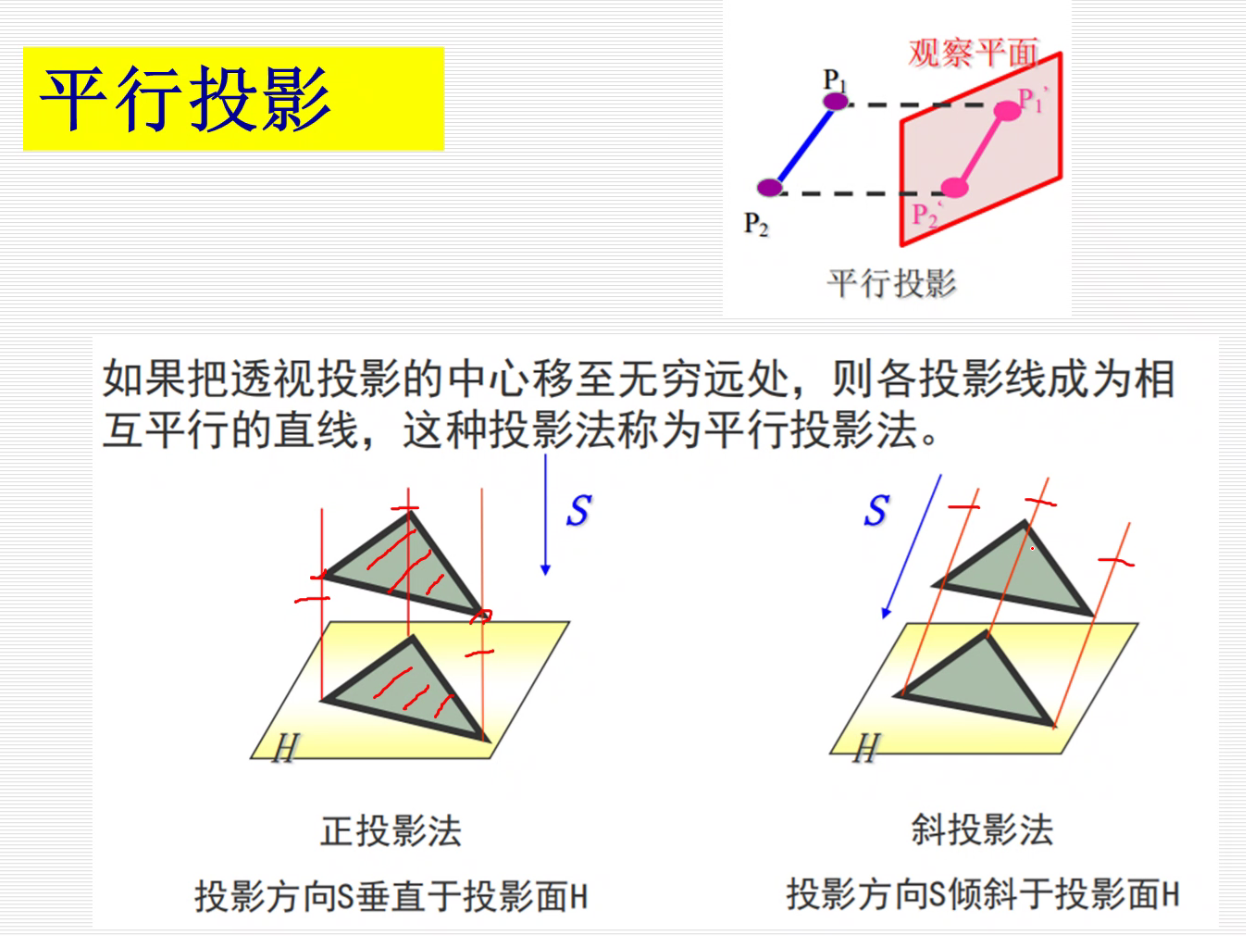
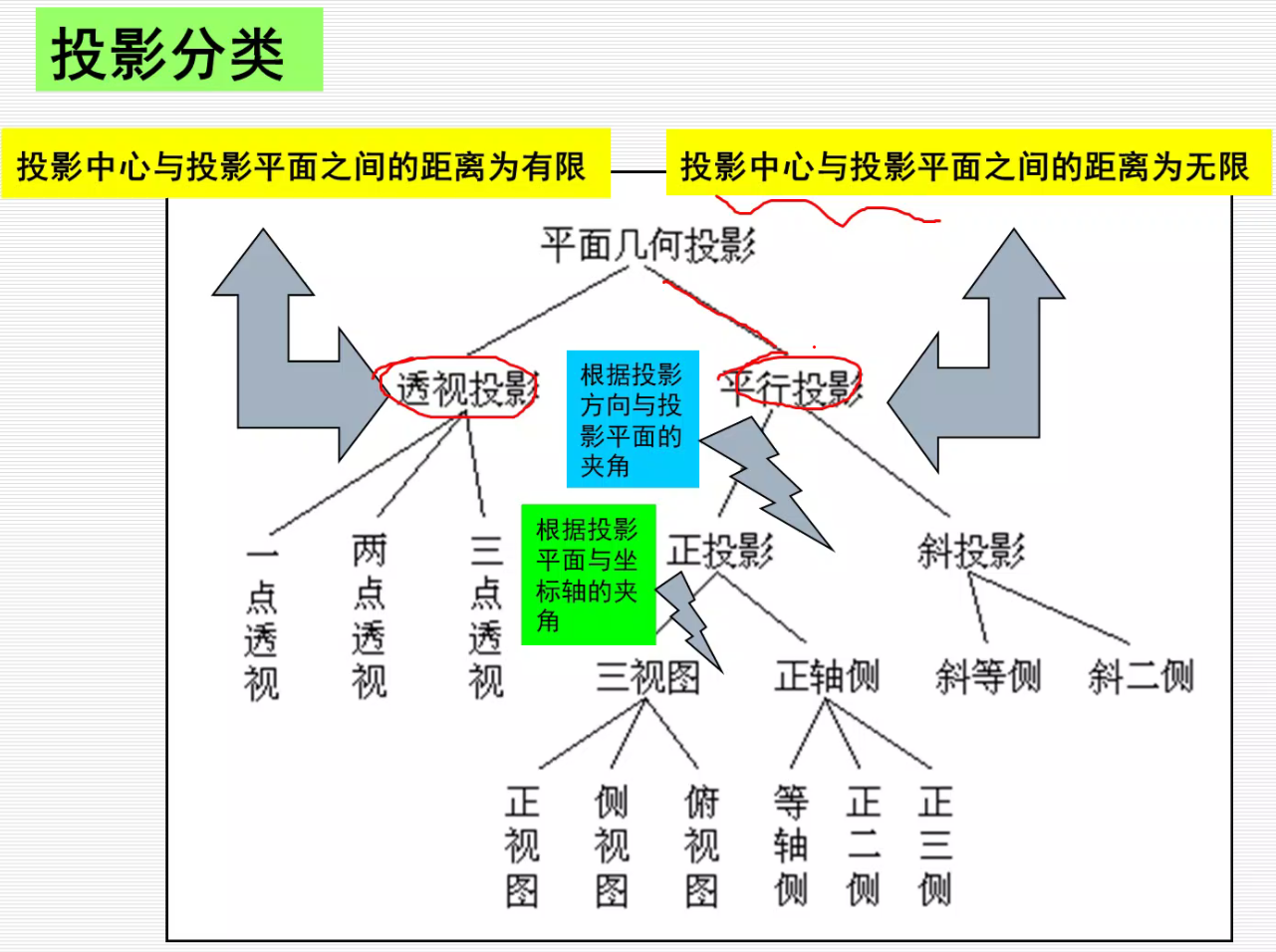
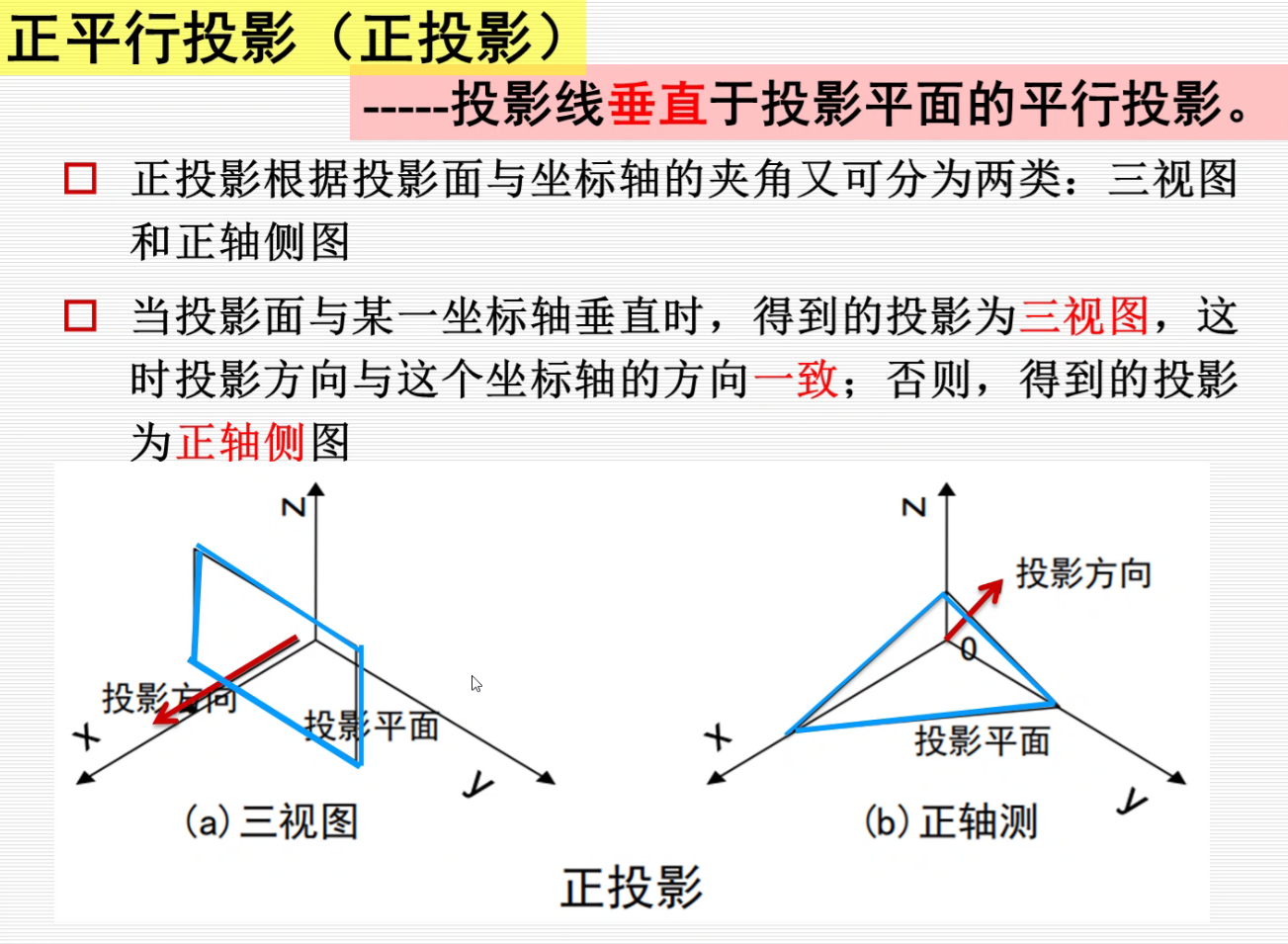
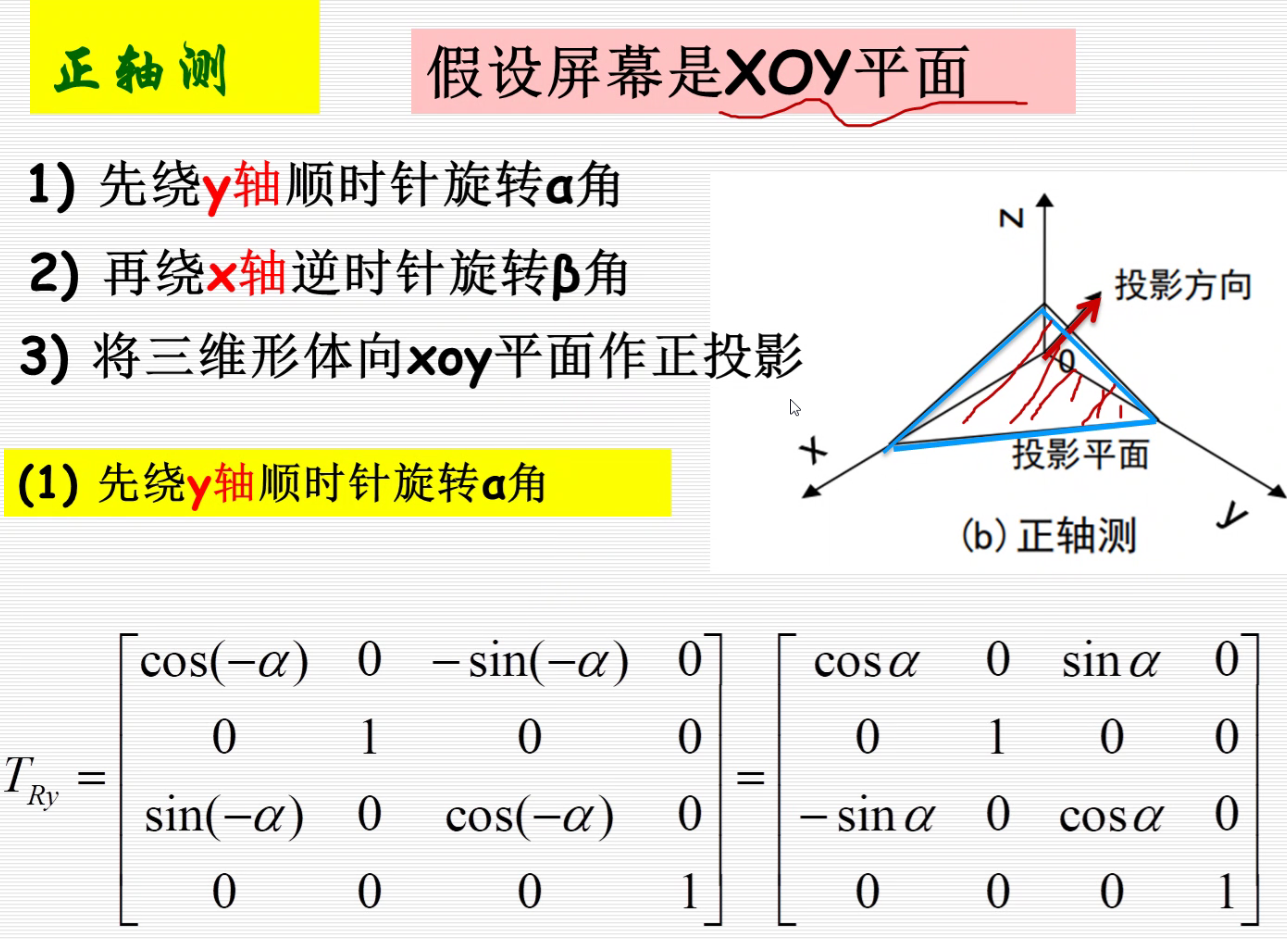
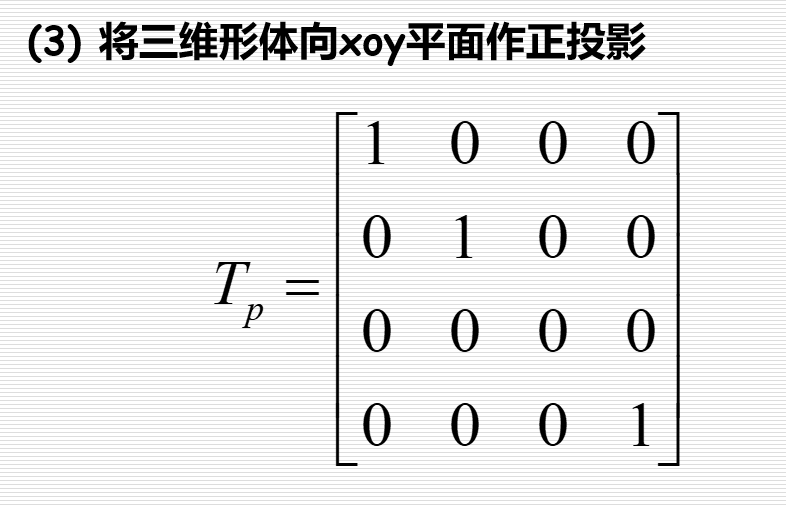
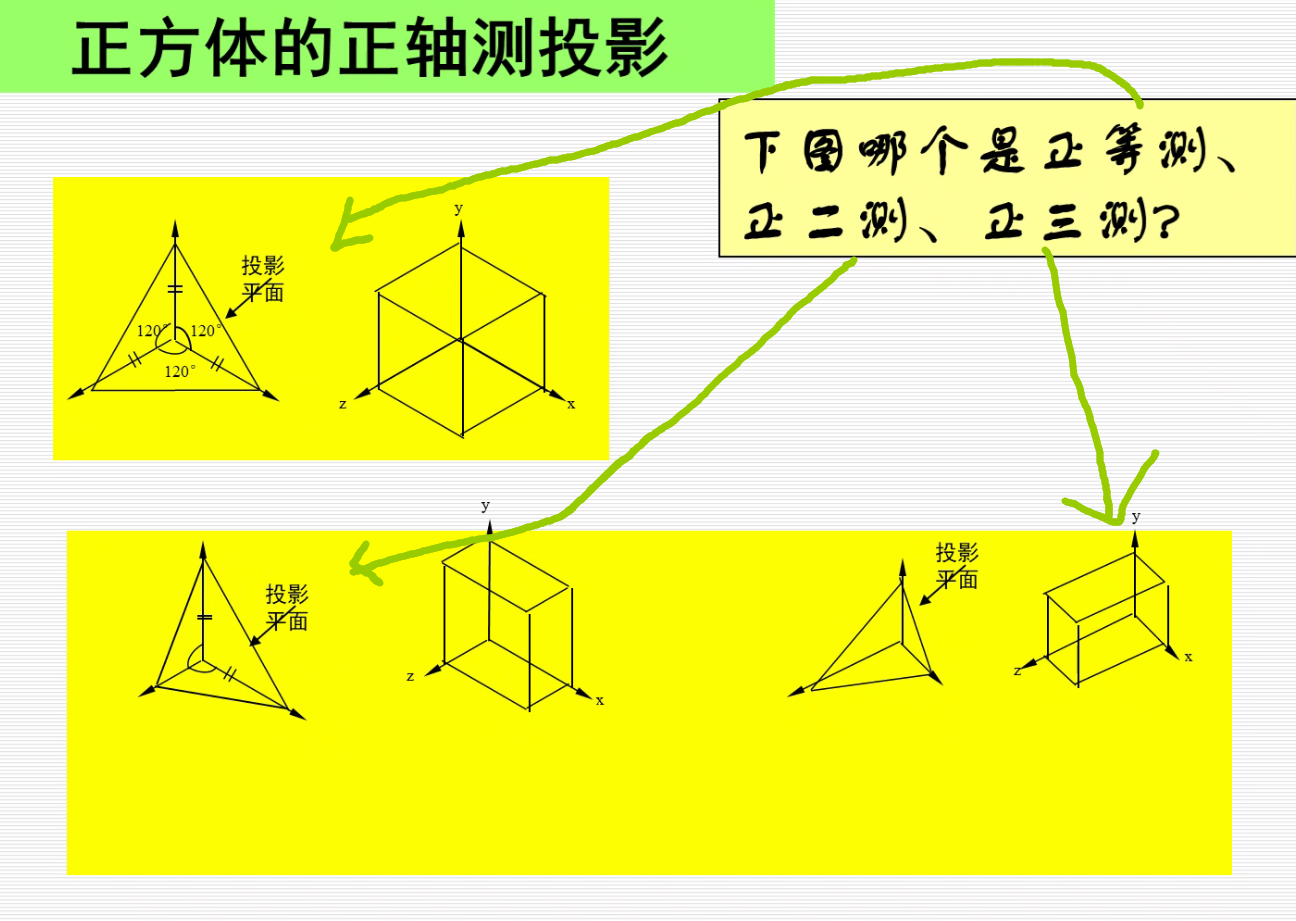
正投影
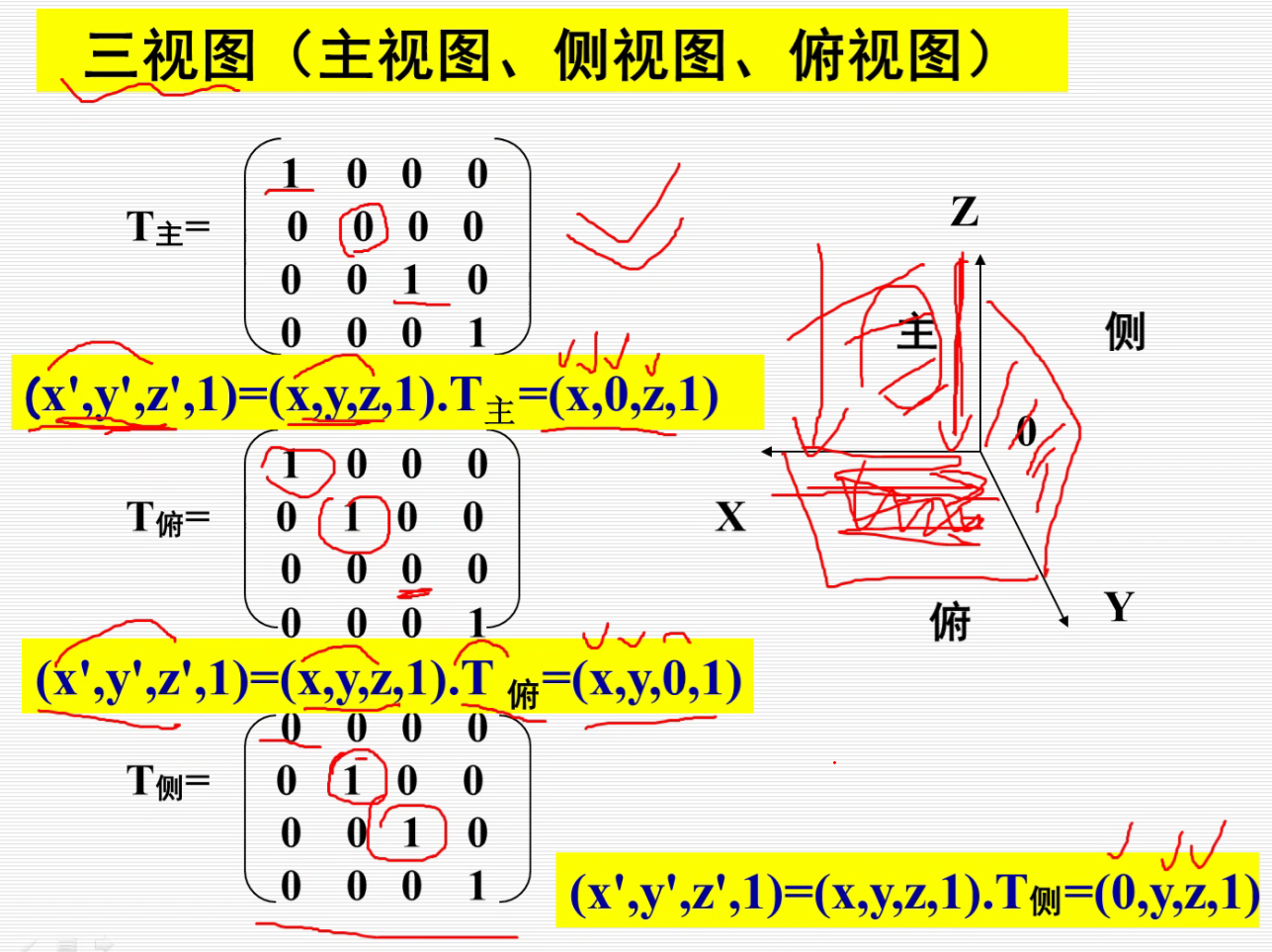
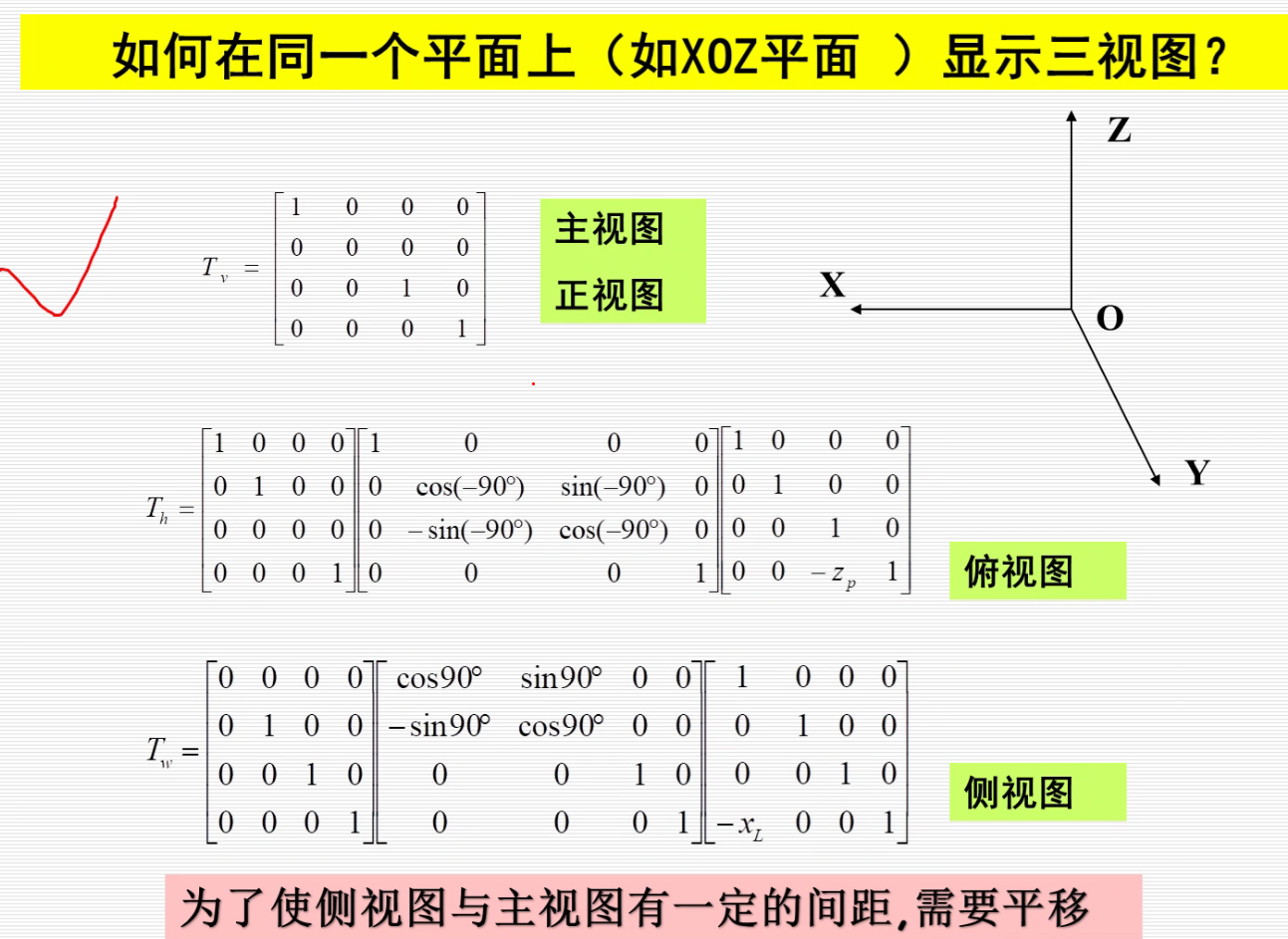
为了在一个面上,可以做如下处理:
俯视图即: 先投影到XOY面上,然后绕着x轴旋转-90°。
侧视图:先投影到YOZ面上,然后绕着Z轴转90°。






斜投影
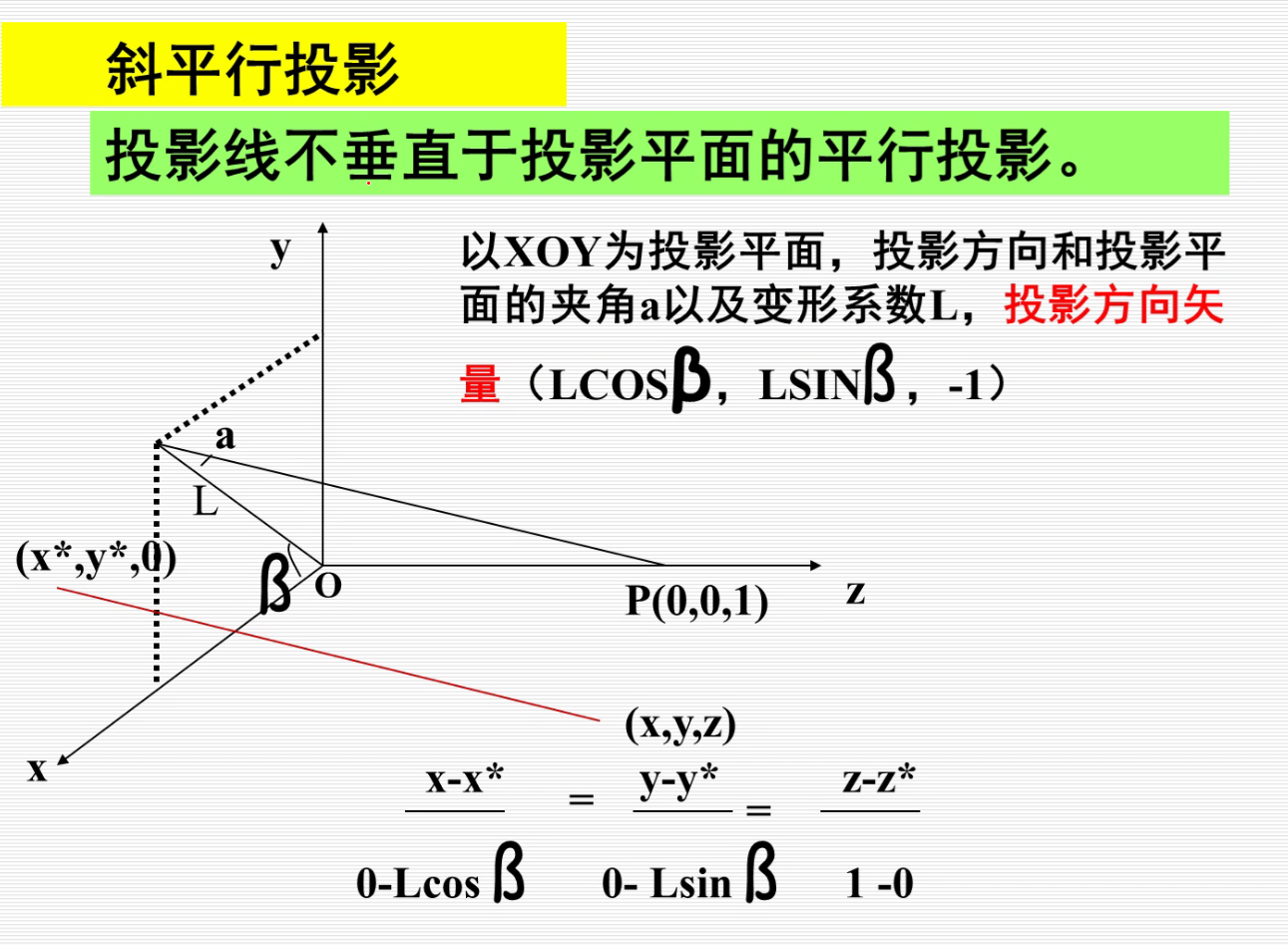
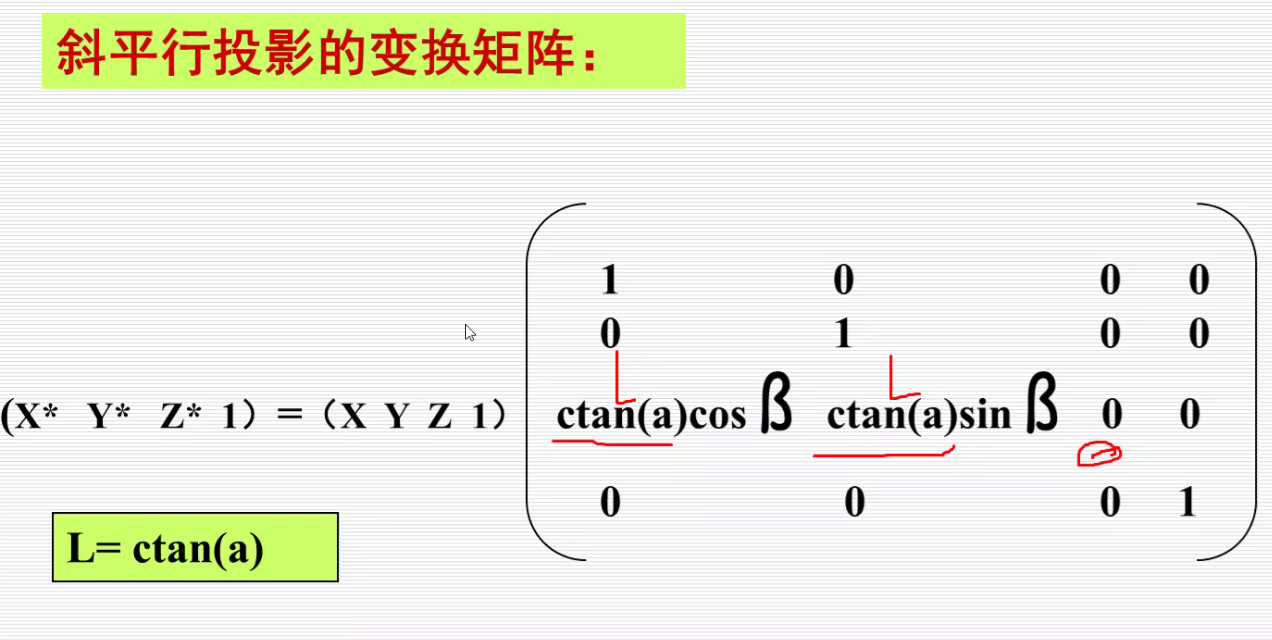
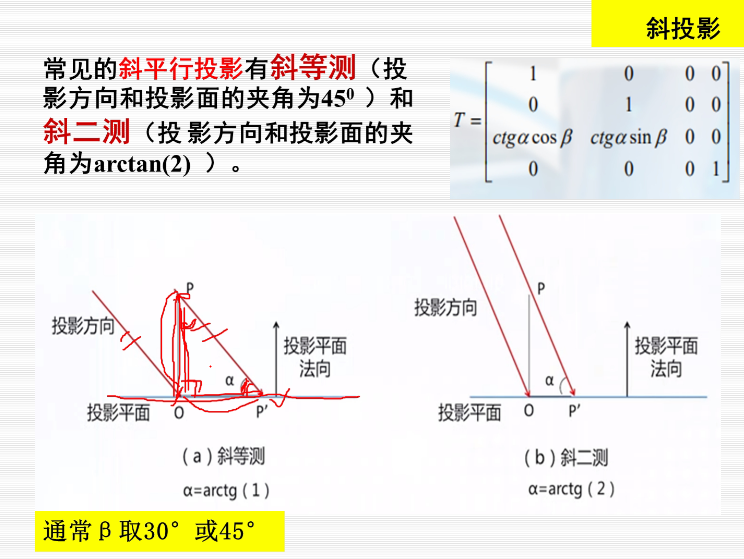
斜等测的投影和原来物体长度相等,而斜二测不相等,斜二测是op=2op’,变为原来的1/2。
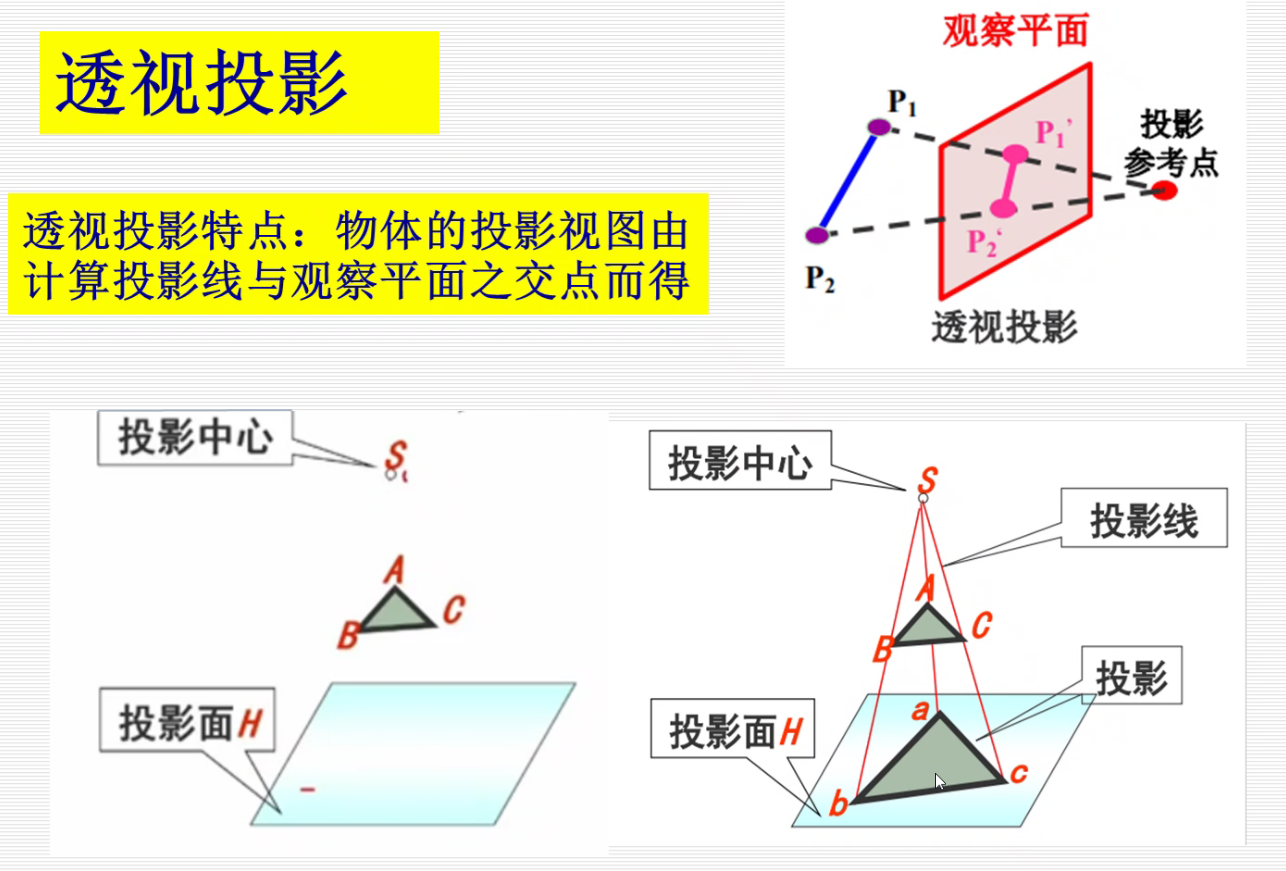
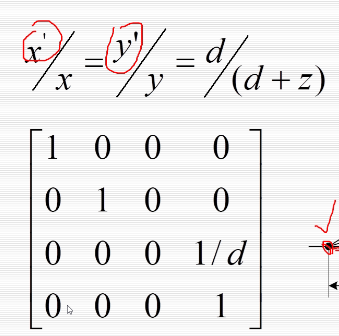
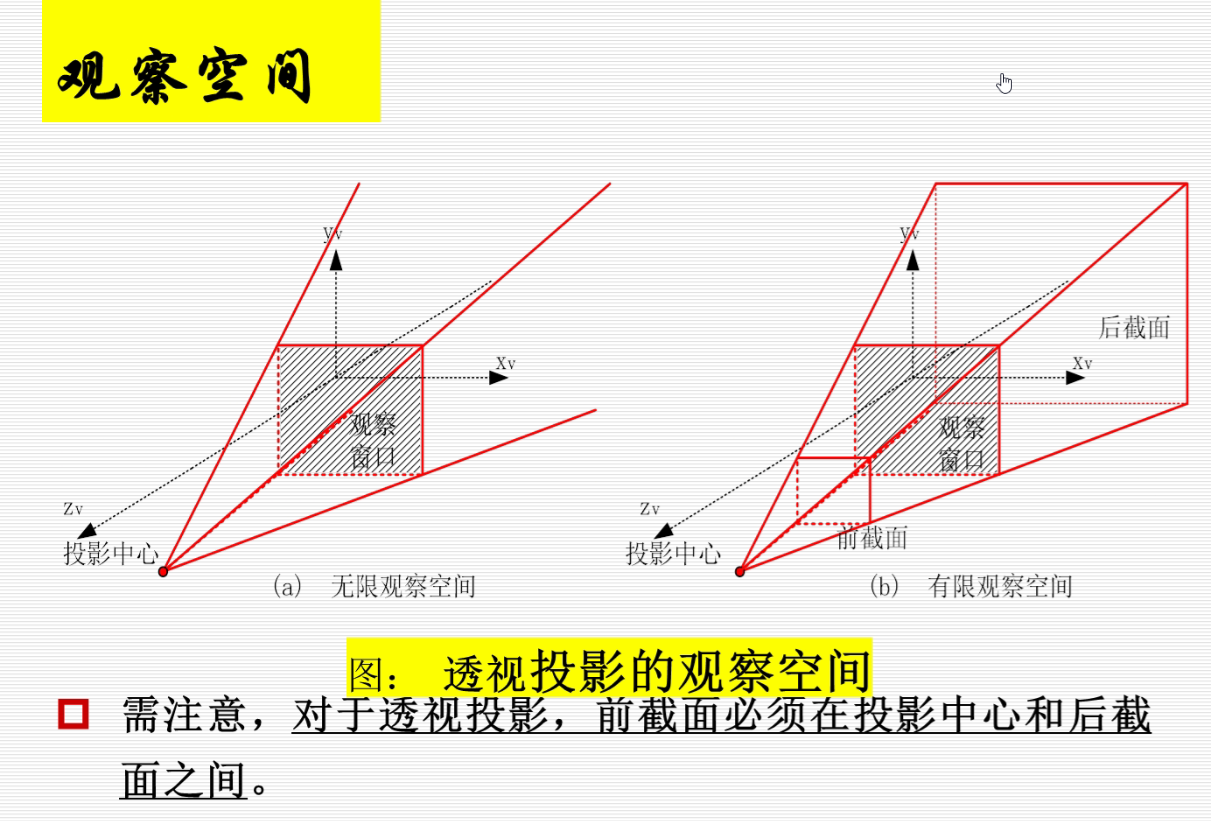
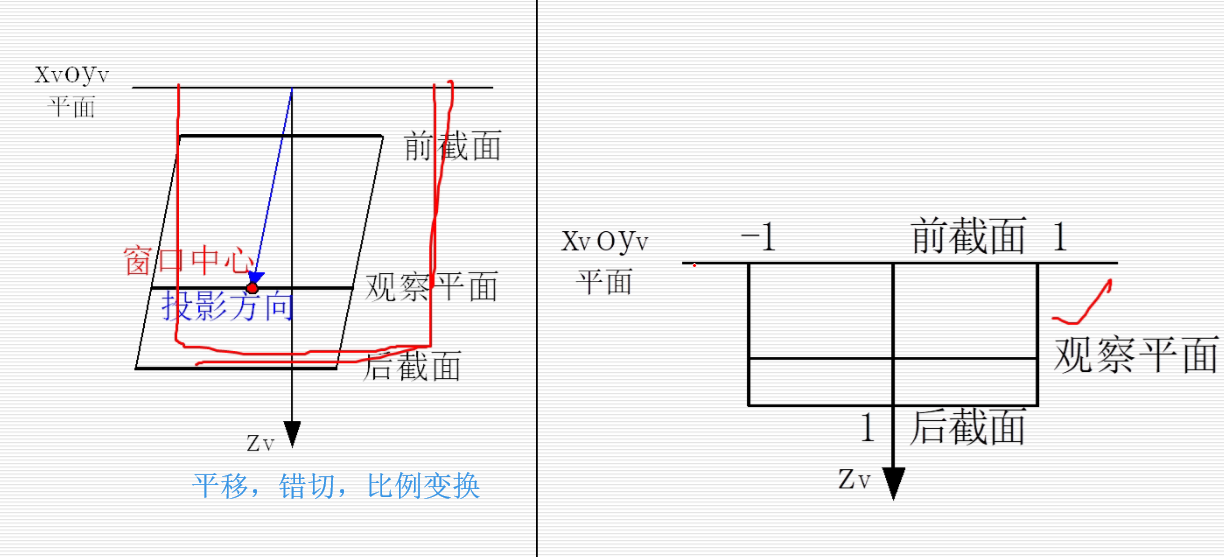
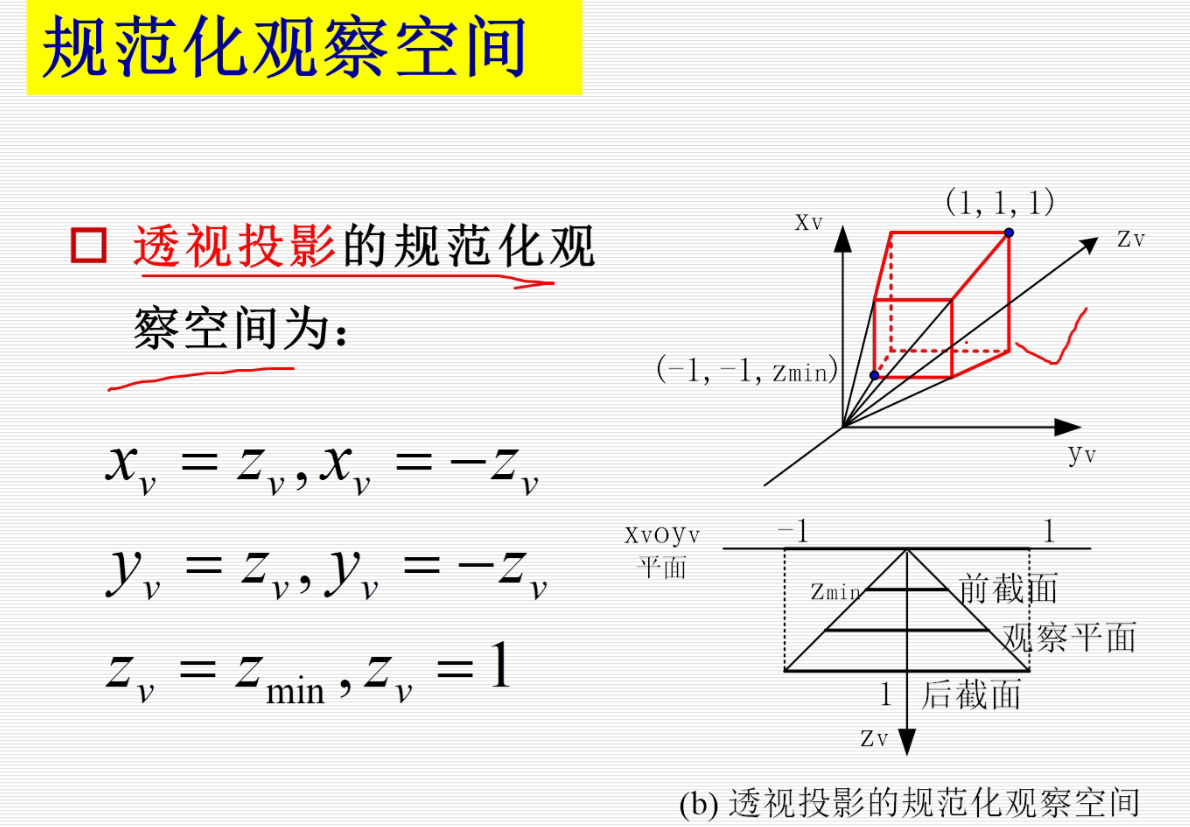
透视投影:
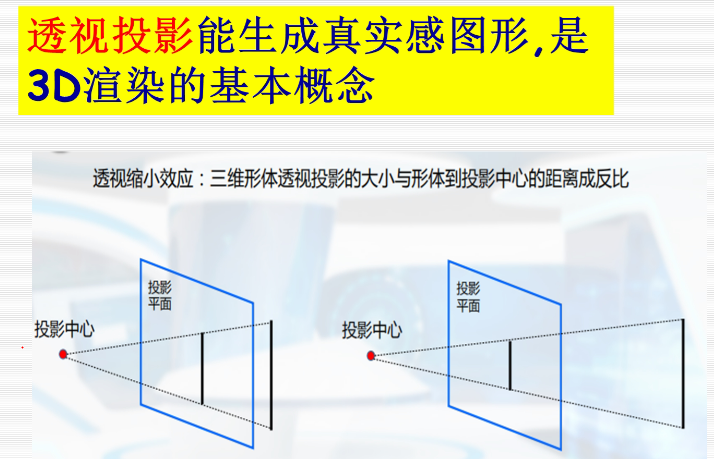
投影平面上的是投影,后面的是物体。当后面的物体往后移,投影变小。透视投影可以产生近大远小的特点。
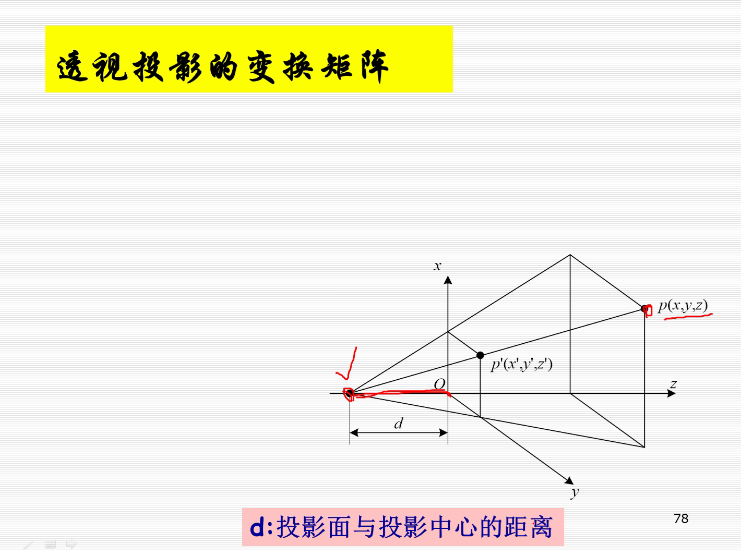
由相似关系可得变换矩阵:
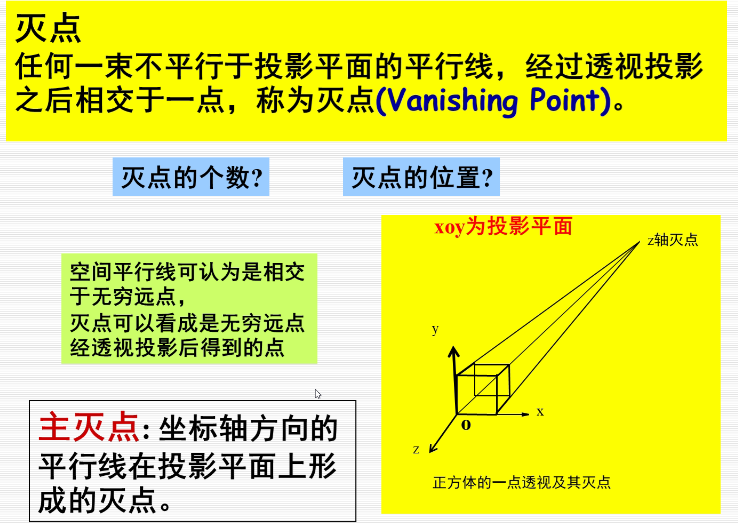
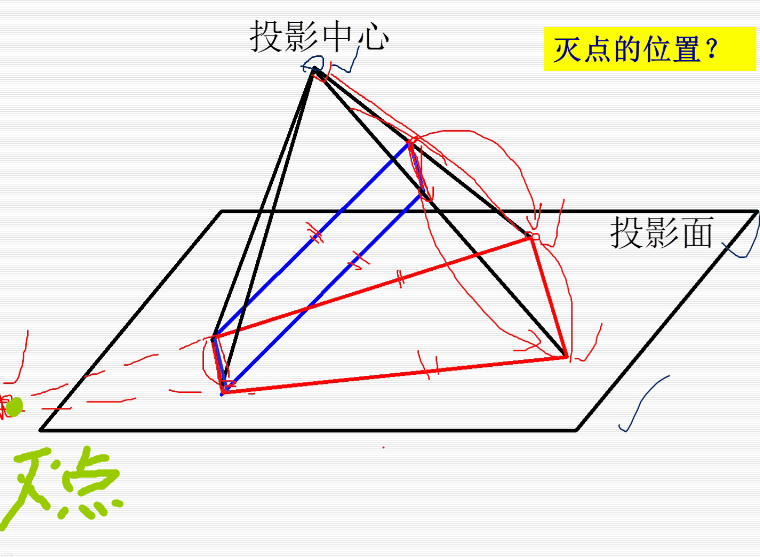
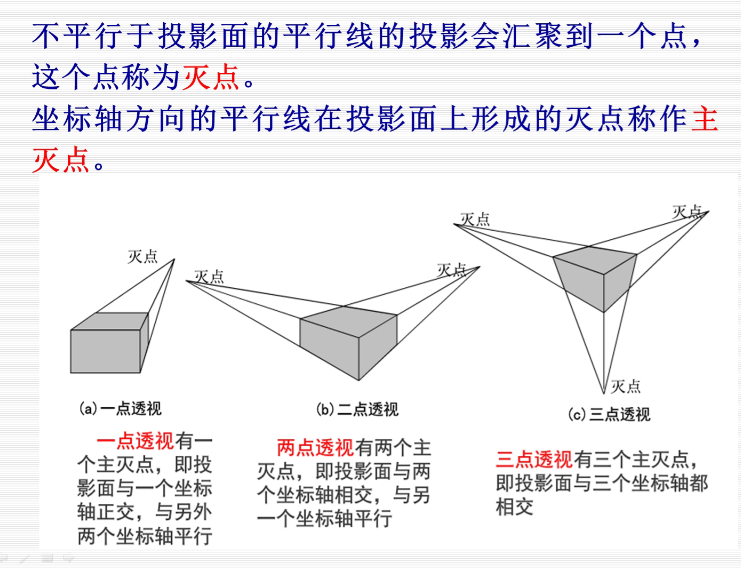
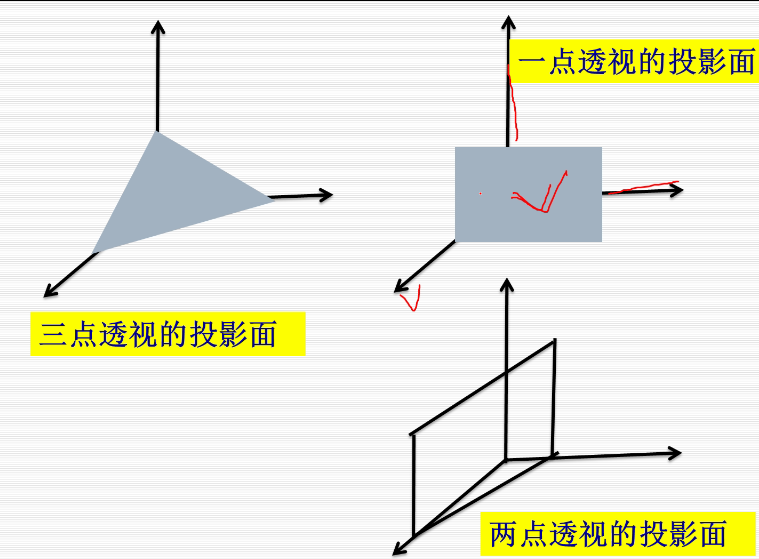
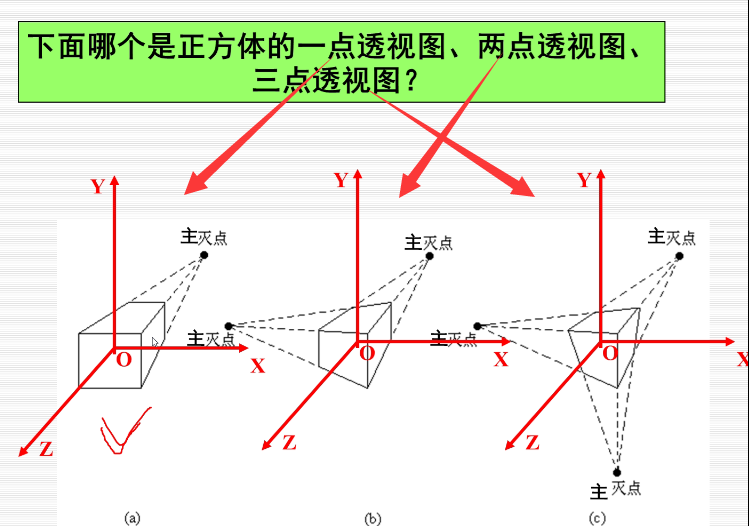
在上图中,投影平面为XOY,正方体中和投影面不平行的只有侧着的四个边,他们相交于一点,即为灭点,又因为这四个侧边是作汴州方向的平行线,所以这个灭点还是个主灭点。
第八章:曲线和曲面
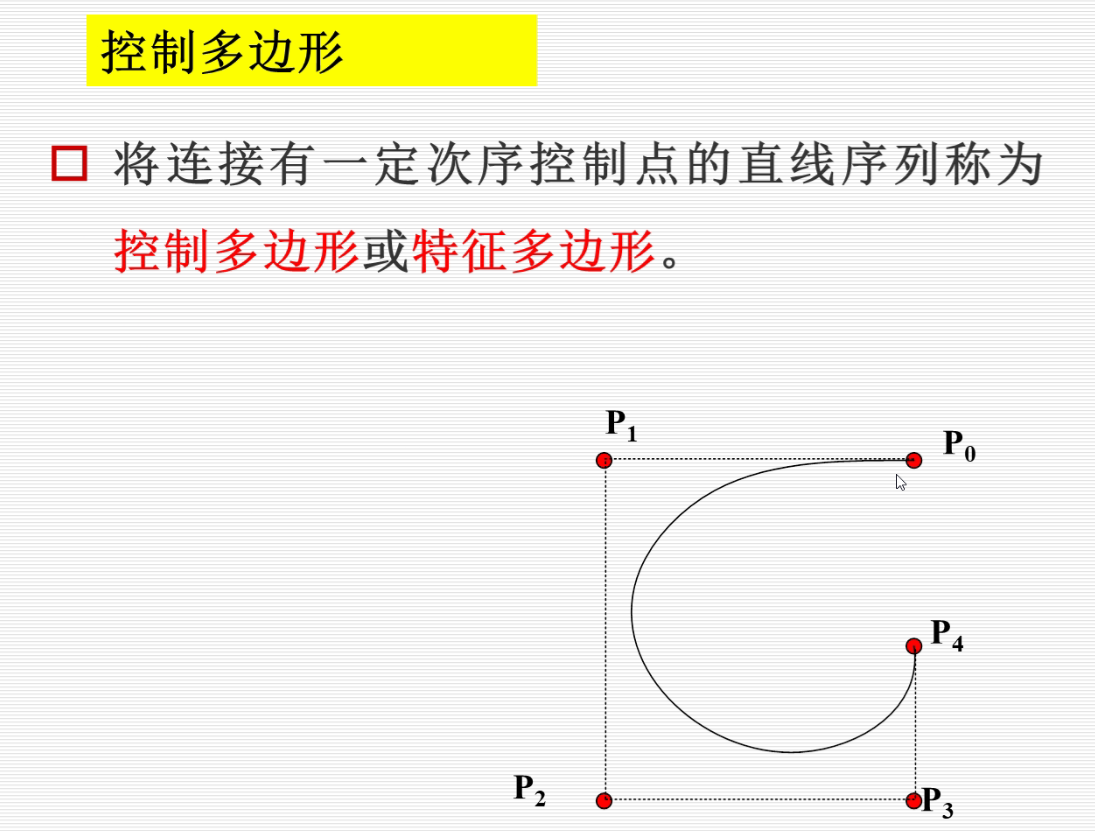
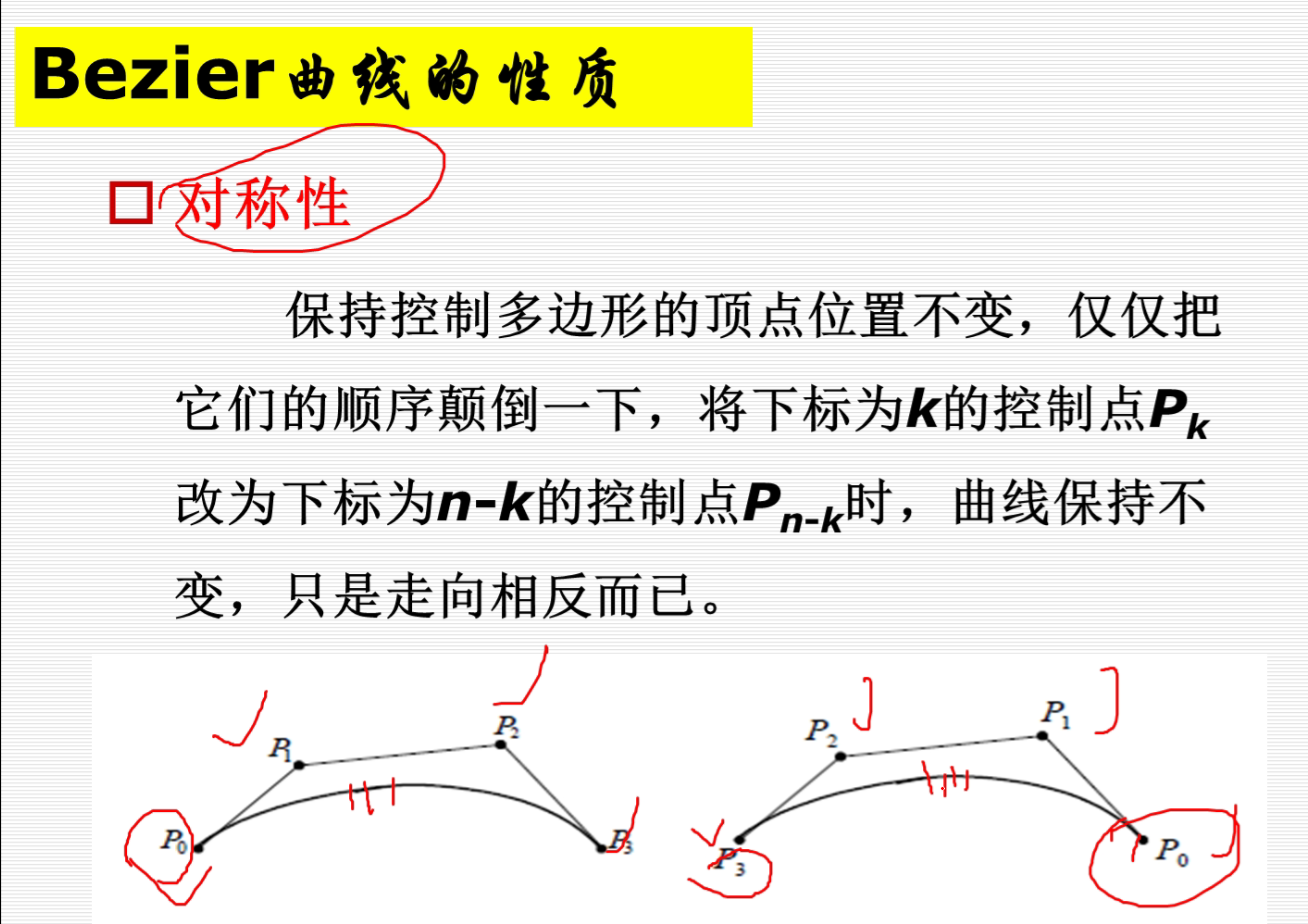
我们称:将连接有一定次序的控制点的直线序列称之为控制多边形 或者 特征多边形
曲线可以用单个参数来表示,例如:




比如线性插值: 是指两个不同点x1,x2,用一个线性函数y=ax+b近似代替,称为线性插值函数
抛物线插值:三个不同的点x1,x2,x3的函数值分别为y1,y2,y3,要求构造一个函数 $f(x)=ax^2+bx+c$,使得抛物线f(x)在x=x1,x2,x3时与y1,y2,y3的值相等。(其实就是要求抛物线经过这三个点)

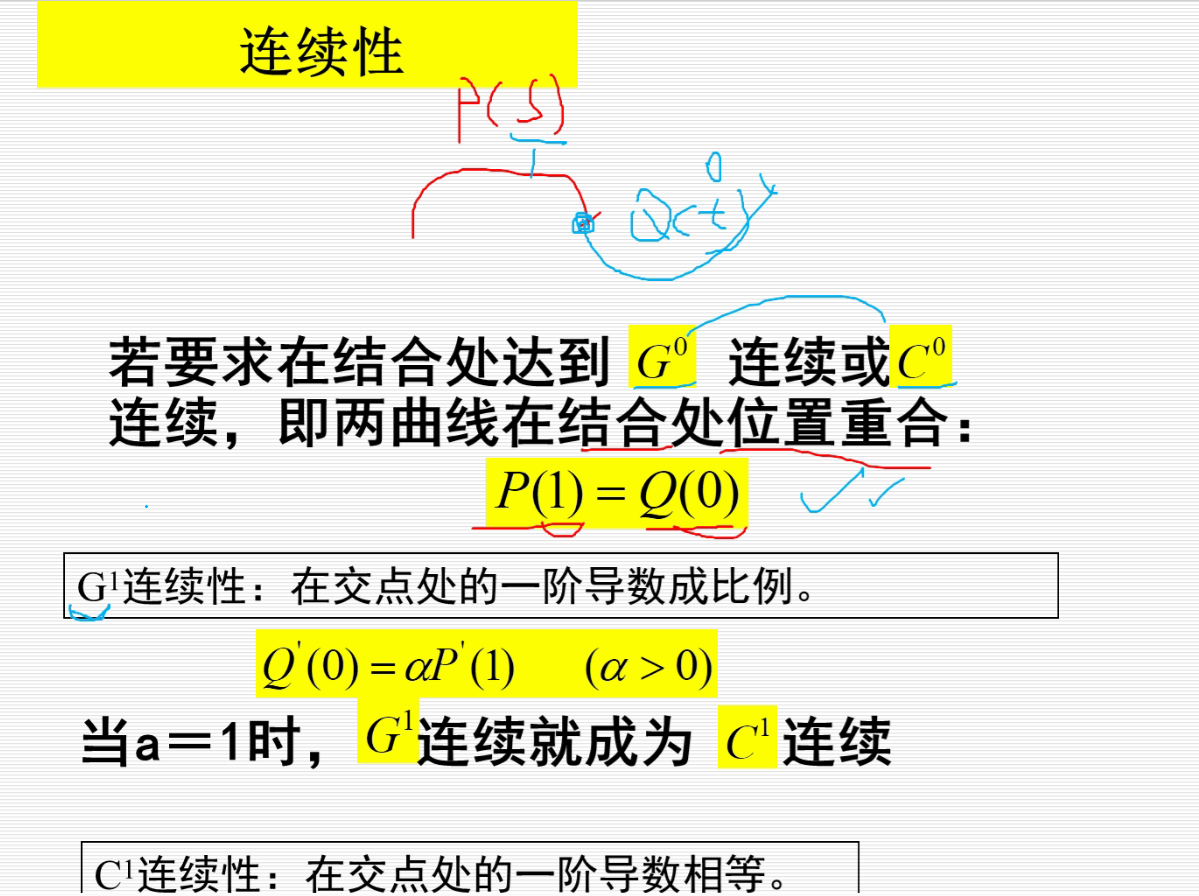
参数连续性:一阶参数连续性中的α为1时,即交点处一阶导数相等,此时即为一阶参数连续性,α为n,代表n阶导数相等(0阶参数连续性就是指连接点处的函数数值相同)。记为$C^n$
n阶几何连续性: 1.2.3…n阶交点处导数都成比例,且比例相等。 (0阶几何连续就是交点处函数值相同)



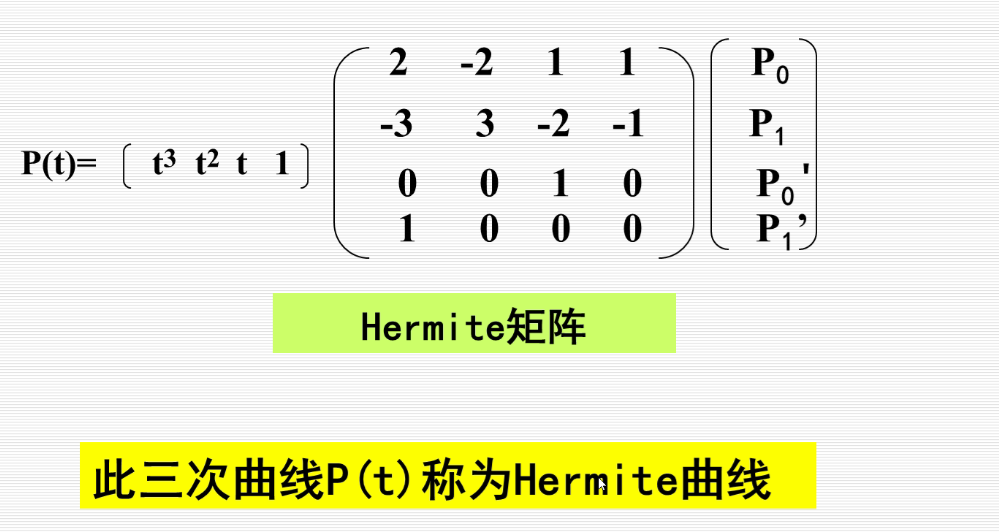
记住下图的矩阵:

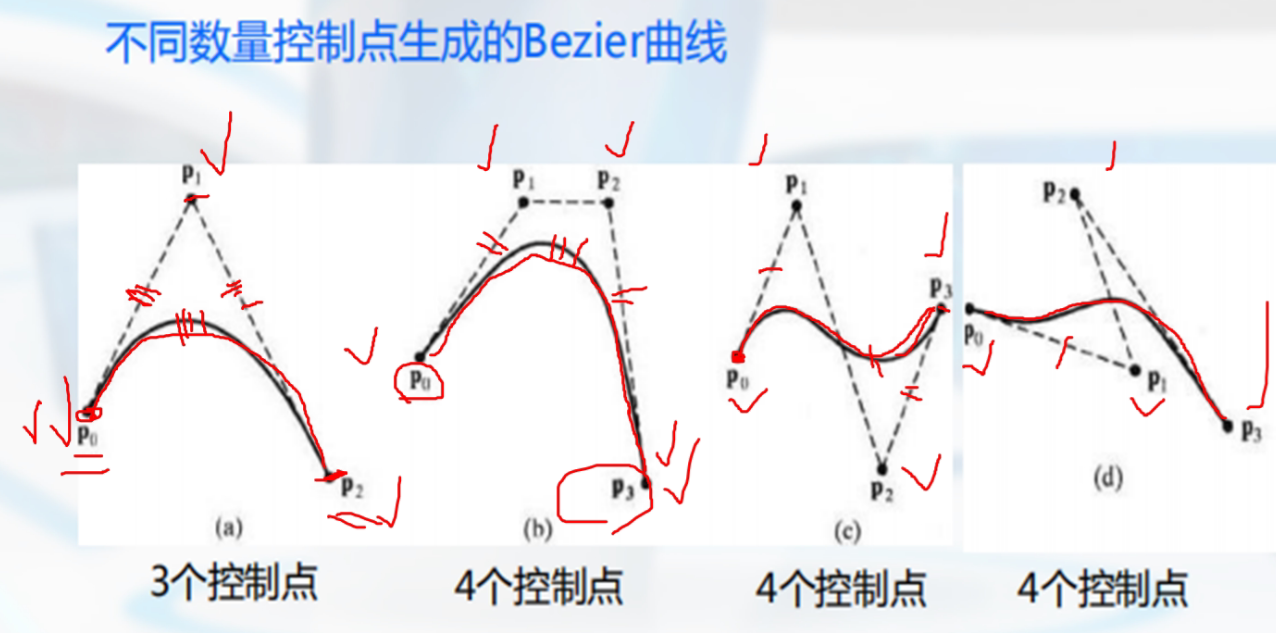
n+1个控制点可以构造n次的贝塞尔曲线
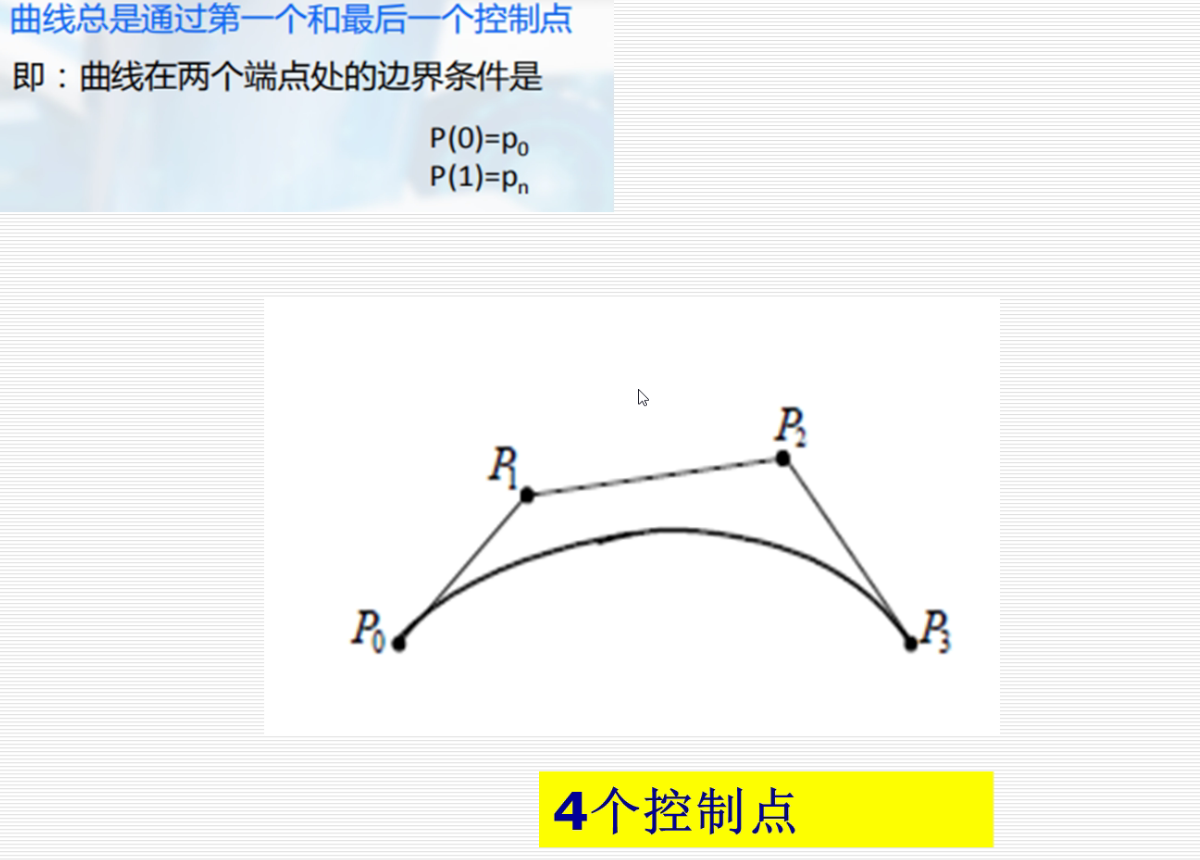
首尾相连的曲线,p0和pn重合

一次贝塞尔曲线是一条直线段 $p(t)=(1-t)p_0+tp_1$

是一条抛物线,记住上述矩阵


是一条三次曲线,记住上述矩阵
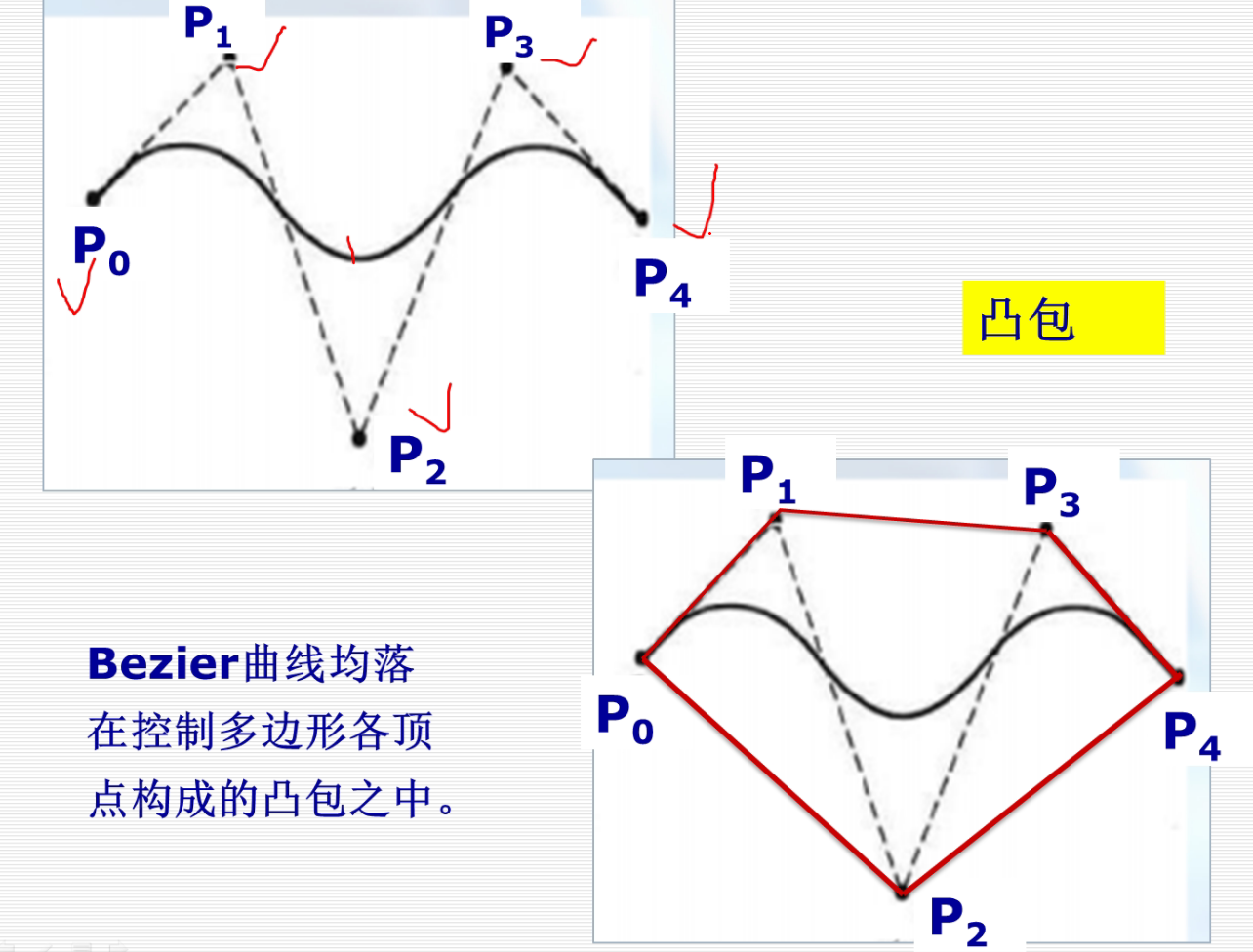
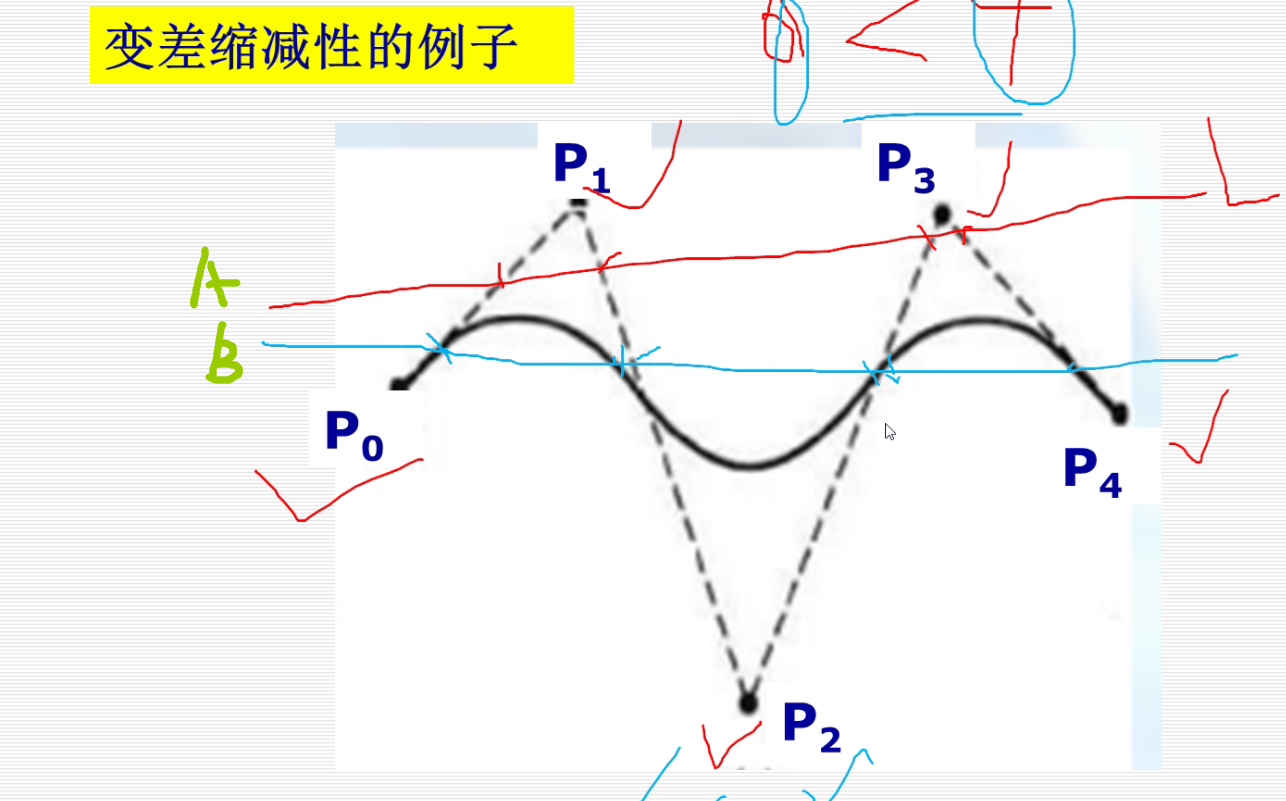
虚线的变化幅度明显大于实现,所以缩减性变差
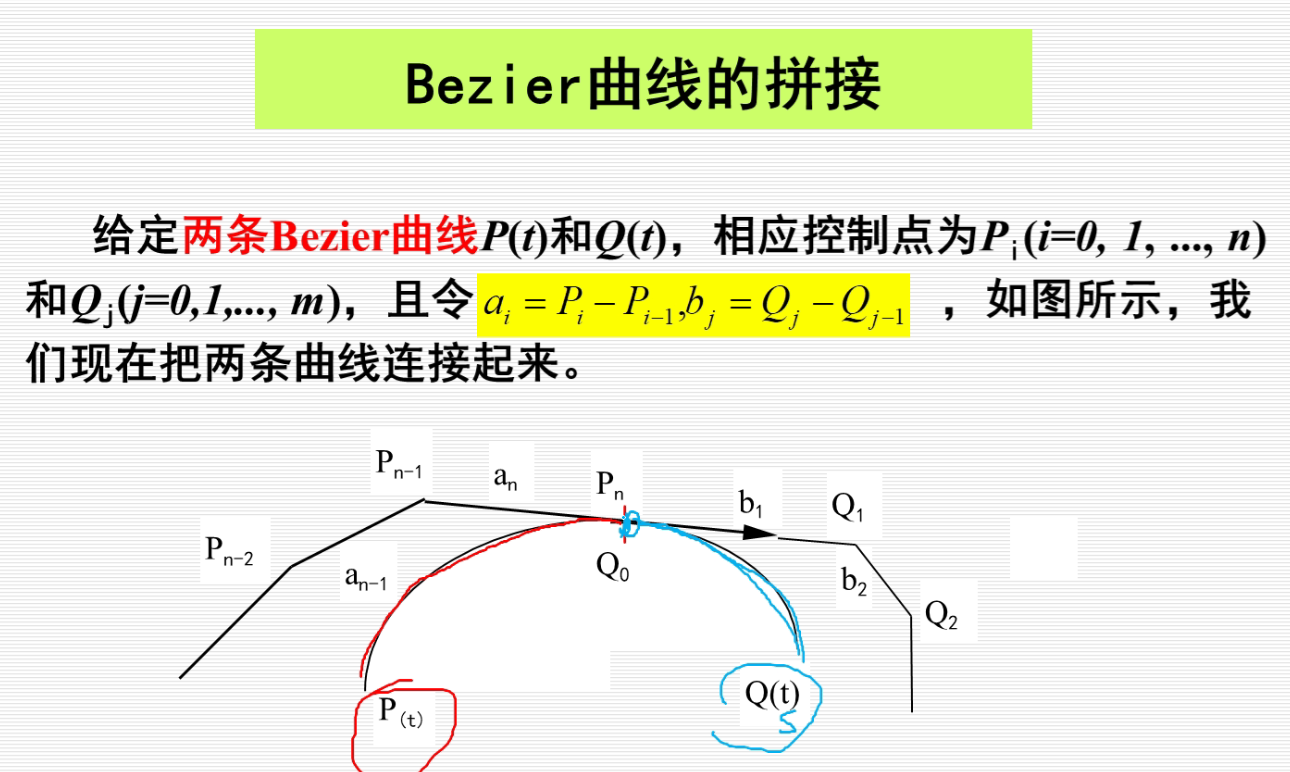
bezier的缺点就是一个整体逼近的方案,很难实现局部的修改





第九章:消隐
消隐的对象是三维物体



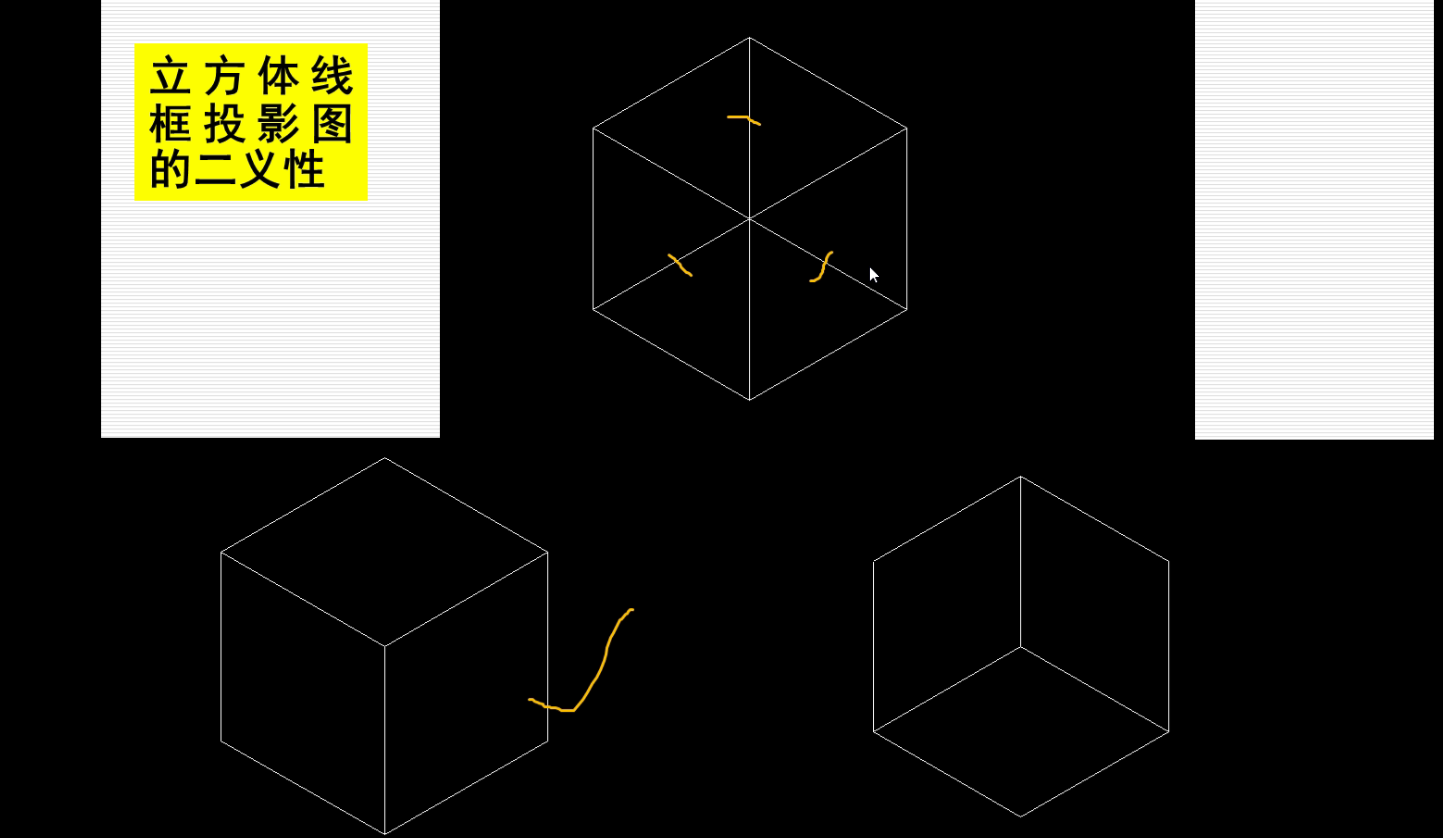
深度排序算法(画家算法)

先远后进

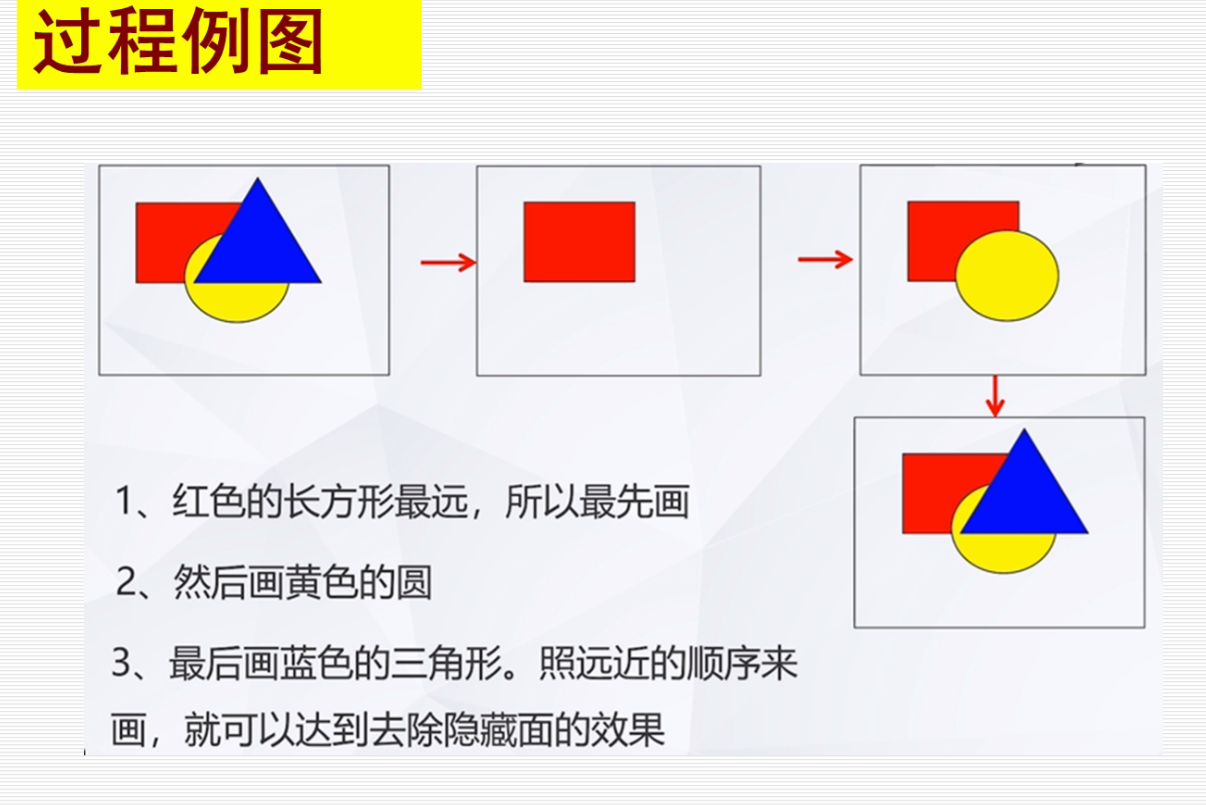
深度缓存算法(z-buffer)




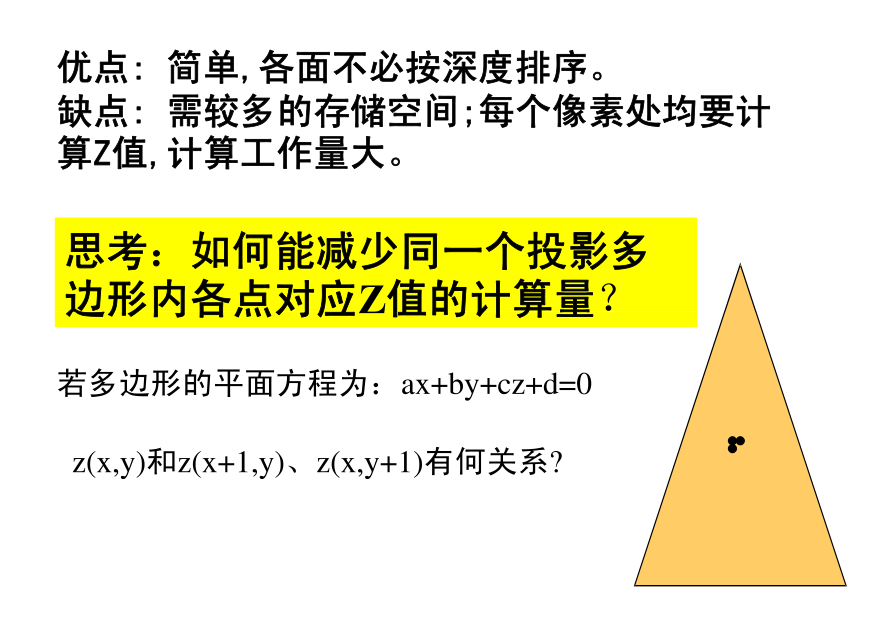
z(x,y) z(x+1,y) z(x,y+1)互相差一个常数,因此可以已知一个点后去递推其他的点。这样就减少了z值得计算量。
z-buffer算法缺点还有:在实现反走样,透明和半透明等效果方面有困难。
总结一下z-buffer method:
他用了两个数组,FB颜色数组和ZB深度数组,对于每一个图形的像素点,首先看这个像素点的深度Z(X,Y)是否大于当前点的ZB(X,Y),如果大于则更新该点的颜色数组和深度数组:FB(x,y)=该图形上这个像素的颜色,ZB(X,Y)=Z(X,Y)
区间扫描线算法
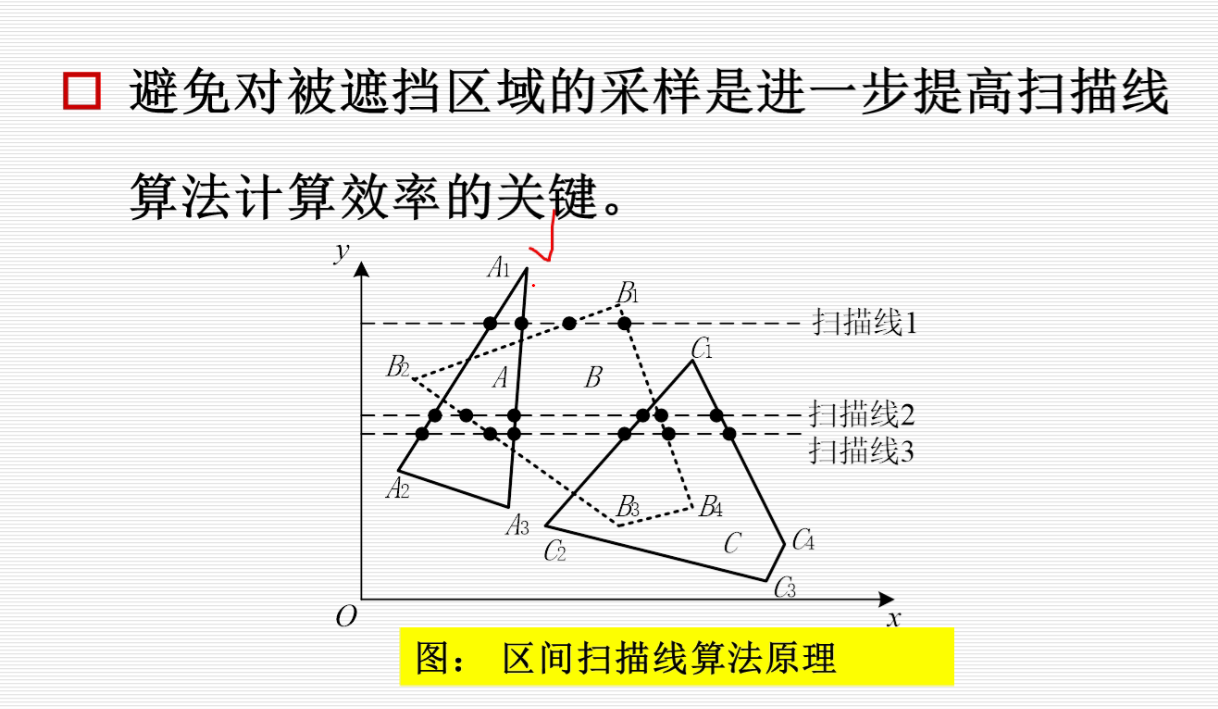

这个算法主要是为了加速Z-buffer算法的,因为z-buffer本来要一个一个像素来计算的,现在它通过边表找到一段区间都是同一个颜色,且深度都一样,因此大大加速了相似点的计算。
区域细分算法
这算法也是为了加速,分成多种情况分别处理。


光线投射算法(了解)
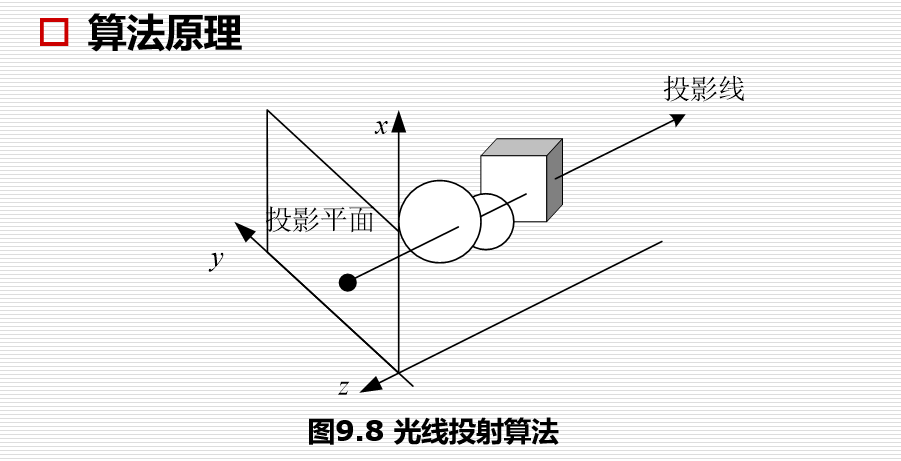

感觉和上面z-buffer没什么区别,就是变成了三维的了。

BSP树算法(不考,懒得写了。。)
第十章:真实感图形绘制
简单的光照模型
简单的光照模型中只考虑反射光的作用。
反射光由环境光,漫反射光和镜面反射光三部分组成。


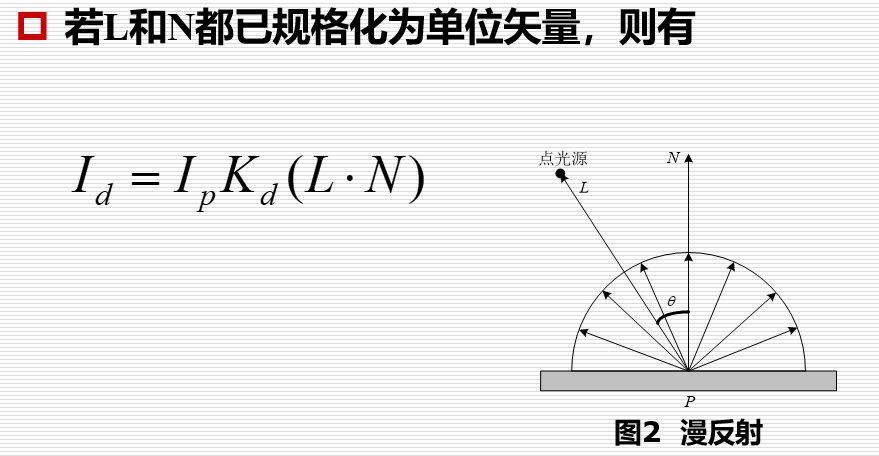

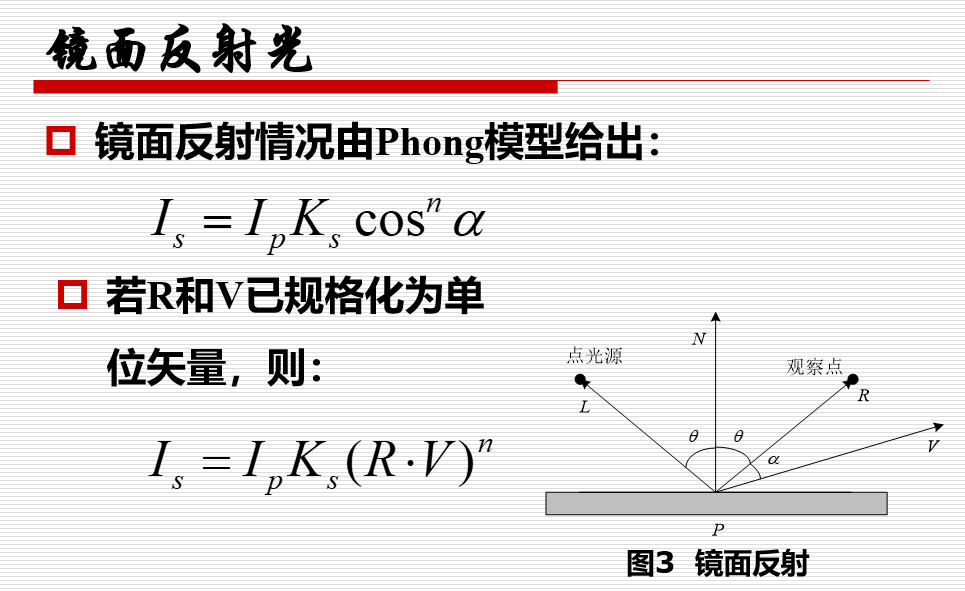

以上都是理想情况,实际中:光在传播中能量会衰减,因此我们要考虑模型中光强的衰减。



RGB颜色模型就是在原来的计算公式中,将rgb三色拆开来算。
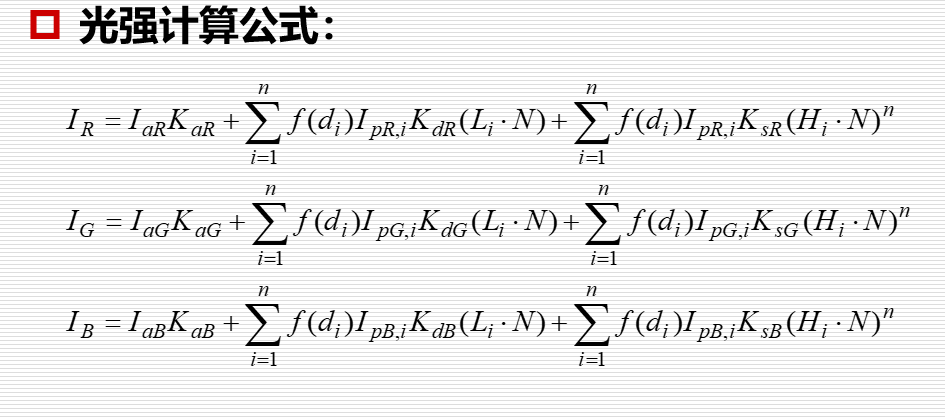
基于简单光照模型的多边形绘制
恒定光强:

Gouraud敏感处理:
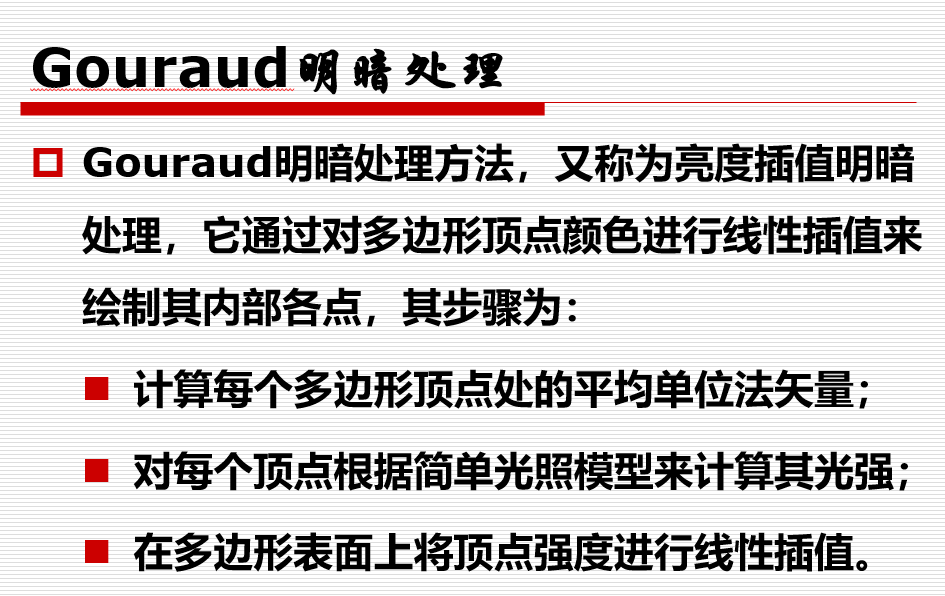
缺点:双线性光强插值解决了相邻多边形之间的颜色突变问题,镜面反射效果不太理想,相邻多边形的边界处的马赫带效应不能完全消除

Phong明暗处理

和gouraud的区别是,phong先对多边形内部通过双线性插值确定矢量,然后再用光照模型确定内部光强。
透明处理:
简单的透明处理是不考虑折射的。
但实际上透明表面的光强包括反射光和折射光。
产生阴影:


模拟景物表面细节

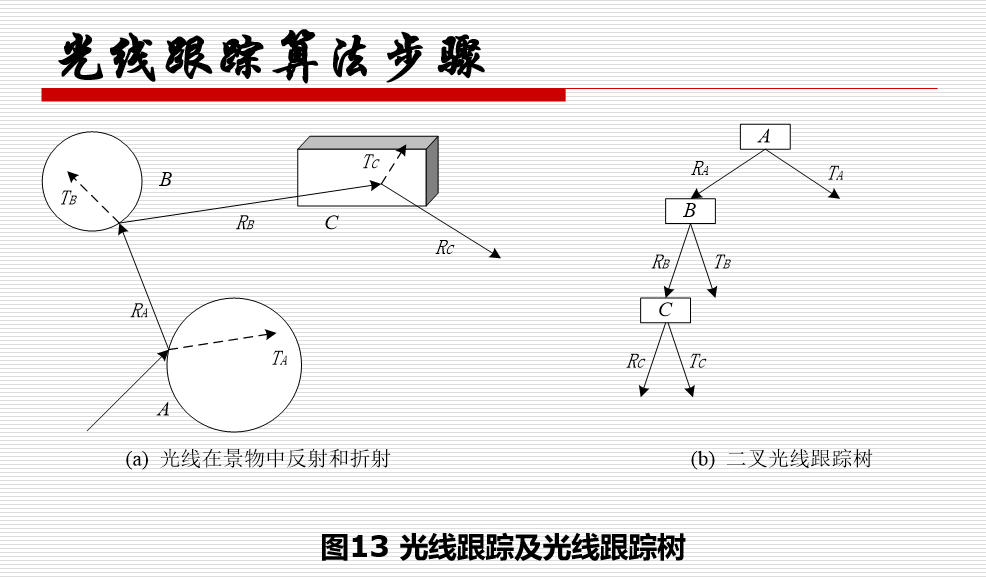
整体光照模型和光线追踪




本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!