Ch5：Training VS Testing

Recap and preview 回顾

上图是我们所希望做到的。

回到第四章问题：如果$M$变为无限大，怎么办呢？

我们所想做到的：

• 建立一种有限的量替代M
• 证明M为无限时学习的可行性
• 这个$m_H$的选择会帮助我们更好的学习hypothesis的选择

Effective Number Of Lines

我们在以上不等式 用了union bound，但是M无穷大时出了问题。

---

我们看上图可知，一般相近的两个hypothesis的结果是没有什么太大区别的，因此多个h之间很大一部分都是重叠的（如上图：三个圆圈有重叠），而我们的union bound是把他们直接相加的，造成了over-estimating（过度估计）。

---

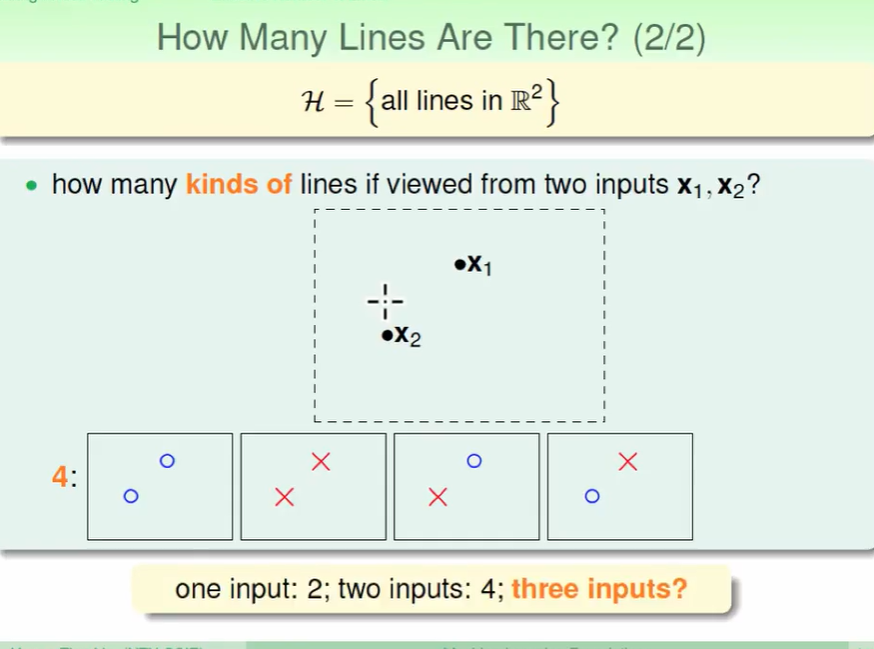
我们来考虑一下上图有几个h，即有几种线可以划分出不同的结果。

不难看出是四种分类结果。

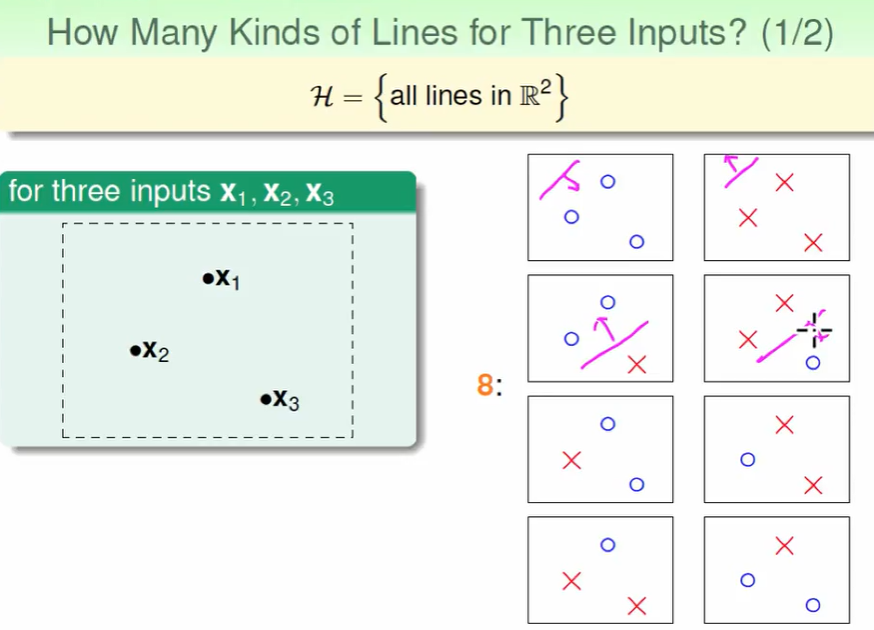
同理，若有三个点，则有8种。那么规律是$2^n$吗？

我们观察下图:

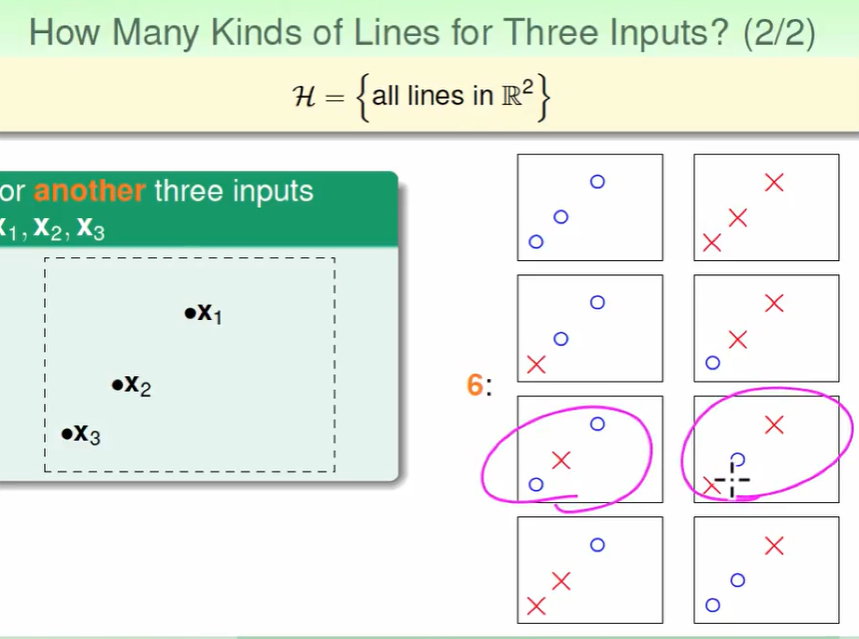
上图我们可以发现，粉色花圈的两个不可能用一条线做到，因此只有6种.

---

对于四个点，其实最多只有14种方式。

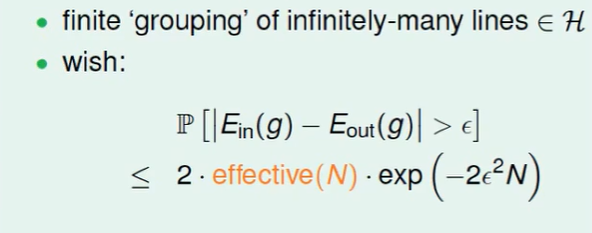
我们猜测：无限多的线可以划分为有限的种类。同种类的线就不需要union bound加在一起了。

希望做到上图所提到的公式，找到一个$effective(N)$

如果$effective(N)$可以做到下的两点，那么我们说学习是可能的。

---

Effective Number of Hypothesis

这里我们引入了新的Dichotomies，他和hypothesis的区别是dichotomies代表种类的多少，是有限的。

---

这里对于不同的样本，线的种类数量可能不是确定的，如三个点，可能是6，也可能是8种。

那么不妨考虑最坏情况，我们取这些不同种类种最大的一个：

即。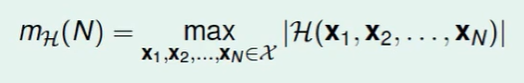

我们称之为$growth \ function$成长函数。

---

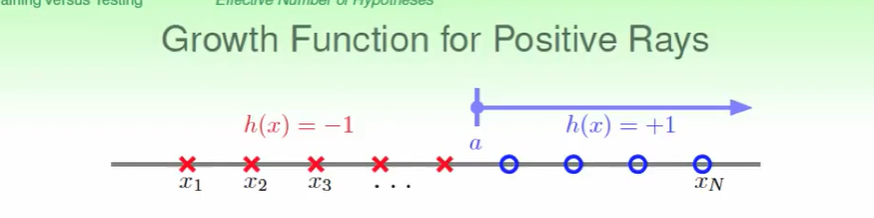
对于这种模型，我们有几种切法呢？

不难发现左边0个，右边N个，左边1个，右边N-1个….. 这样递推，因此：

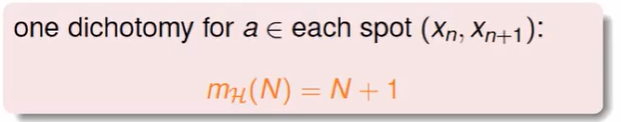
$m_H=N+1$

如果对下图这种h来说：

就有：

这么多种。

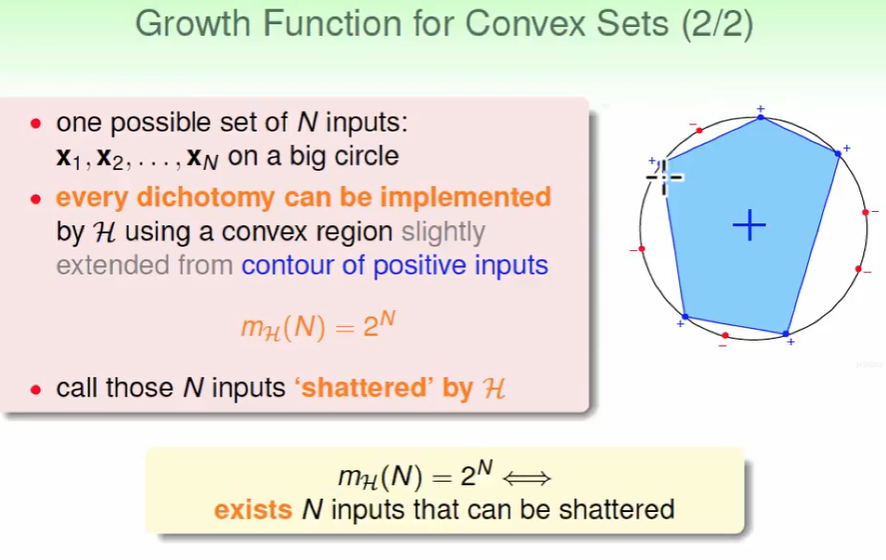
那么如果对于一个 二维的分类，并别h也是区域覆盖，那么$m_H=2^N$,即成长函数growth function为$2^N$。

Break point

我们回顾一下不同模型的growth function的不同。

​ 因此如果M的替代量是一个多项式(polynomial)，那么这是一个很好的替代，它的变化远不及后面e的指数的变化，因此这是可以学习的。但是也有可能是指数型(exponential)的，这就不一定会是可以学习了，因为后面的也是e的指数，在一起可能是不收敛的。

​ 那么对于一个2维感知机问题，增长函数是多项式形式的吗？

---

这里我们引入$break\ point$，在二维感知机分类中，从4个点开始我们发现无法做到$2^N$种情况，即16种，最多只能找到14种，无论这四个点怎么排列。我们称4为break point。

我们观察到，这个break point好像和增长函数有如上的关系，那么真的有吗？下一节会从数学角度解决这个问题。