机器学习基石CH6:Theory of Generalization
CH6: Theory of Generalization
Restriction of break point
还是回到上节,我们做出了以下的猜想:

我们做出了以下的猜想:
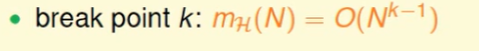
我们思考,当$break \ point = 2$的时候:
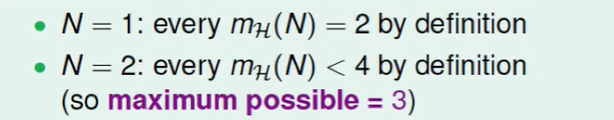
那么 N=1的时候小于break point,所以还是符合$2^N$的规律。
N=2 ,也就是break point,此时 $m_H(N)<2^N$,也就是说$m_H(N)$最大也就是3.
接下来考虑,N=3:

上图这样的情况可以吗?
当然不可以,因为如果此时我们不要$x_1$这个点了,也就说退化到N=2的时候,$x_2,x_3$此时为4种,也就是$2^N$,但是前面说到了,N=2是breakpoint,最多三种。

因此上图这种是不可能的,N=3时,dichotomies变成成上图这样是错误的。
那么我们不难发现,如果要N=3找dichotomies时,要符合N=2的规矩,也就任意两个点不能shatter
(这里的shatter指,情况等于$2^N$,也就是所有情况都存在,而这对于break point是错误的)。
那么我们再接着试一试
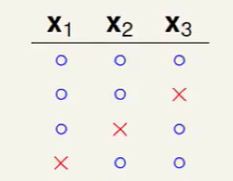
上图这种dichotomies是正确的。
如果接着加就会发现,无论怎么添加也会产生两个点的shatter,所以最大dichotomies也就是4种了。

这么一看,break point严重抑制了$m_H$的增长。
因此接下来我们的证明思路如下:

如果证明了是多项式大小的,那么问题就可以解决了。
最后的课堂问题:
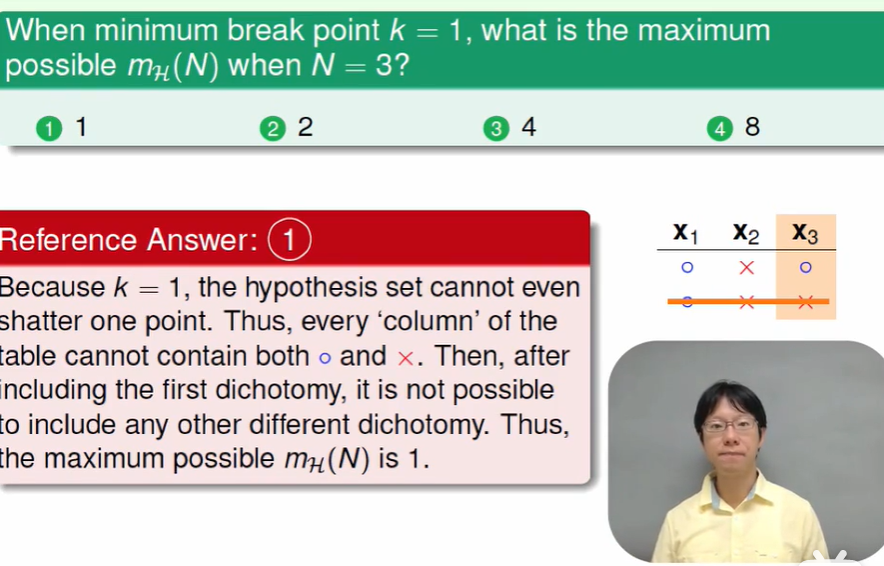
不难想到是1种,因为不能出现某一列有两个不同的,也就是说他们每行都长得一样,即只有一种。
Bounding Function
Bounding Function的定义如下:
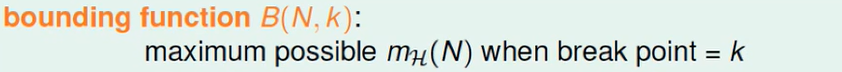
N个点,breakpoint为k时,$m_H(N)$可能的最大值
那么下面问题转化为了:


N<k 不难理解,还没到break point还符合$2^N$规律

N=k,也不难理解
因为此时:$m_H(N)<2^N$,也就是说$m_H(N)$最大也就是$2^N-1$.
N>k时:
我们就要慢慢分析以下这个问题了:

我们枚举以下发现B(4,3)=9 。然后发现 是B(3,2)和B(3,3)的和。
我们把这是11个分类一下:如下图
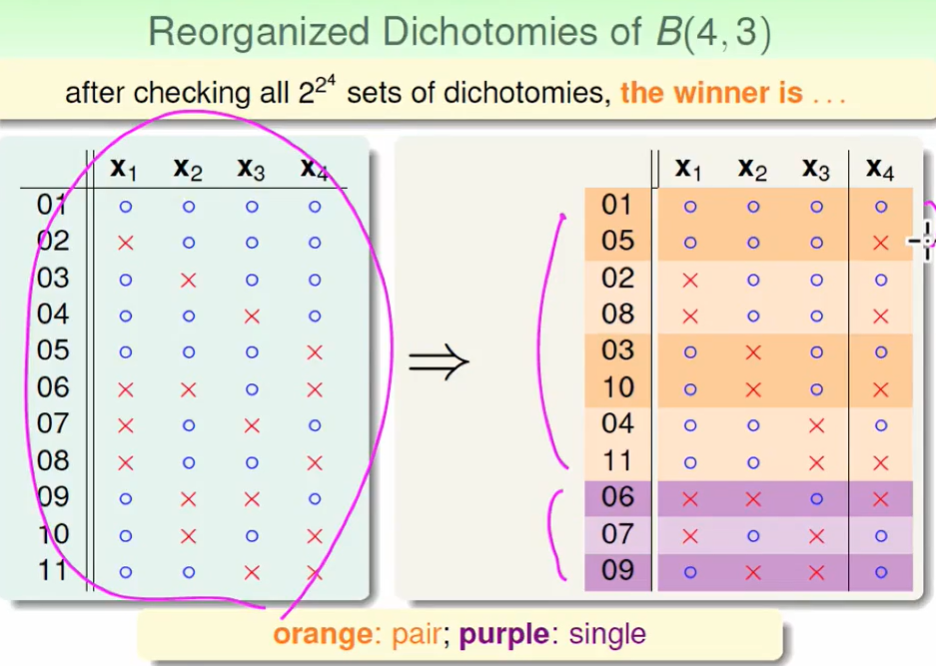
其中B(4,3)的组成成分如下:
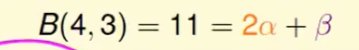
我们可以看出橘色的$x_1,x_2,x_3$ 没两个都是相同的(深橘色/浅橘色),只有$x_4$不同。
我们仅看前三个$x_1,x_2,x_3 $ ,不难得出:
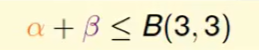
也就是说:4个点则不能出现3个点的shatter。
但是还记得shatter的定义吗,可不是存在,而是任意三个,那玩意三个中包含$x_4$呢?
对于这个问题我们先考虑,去重后的并不包含$x_4$,如下图
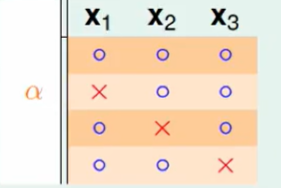
此时如果存在两个x有shatter 加上x_4会对这一列出现 圈圈/叉叉 ,那不就是三个x的shatter 了吗,那就又不符合定义了。因此我们要阻止2个点在橙色区域shatter的出现。
即:
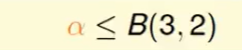
那么我们就可以推出:

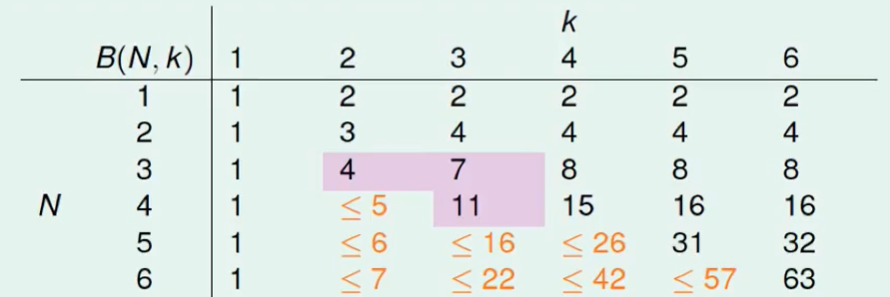
那么对于B(N,k),我们不难推出递推公式:
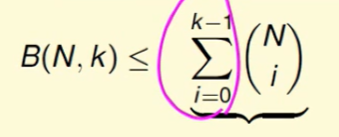
上式其实是一个多项式的,幂次最大的一项是$N^{k-1}$

那么问题到此就解决了。
A pictorial proof(一个形象的证明)

实际上,我们最后得到其实是 浅绿色框中的公式,怎么来的呢? 接下来证明:

$E{in}$的个数不是无穷多个,一共就是$m_H(N)$ 这么多个。而$E{out}$ 是有无穷的多个的。
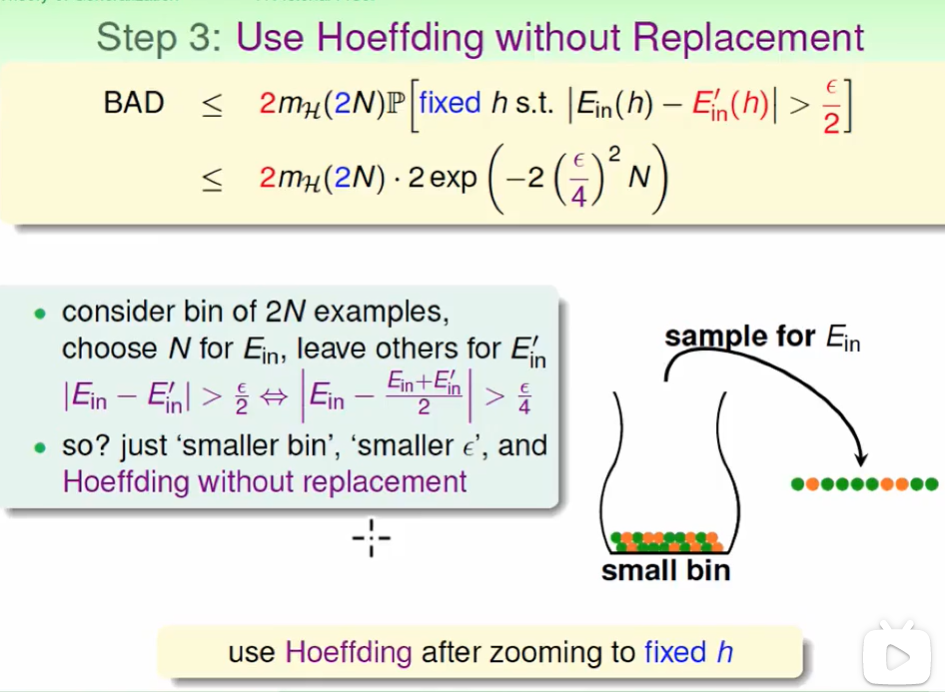
所以第一步我们想把$E_{out}$替换掉:

由于这个E的可能性分布几乎是关于Eout对称的,不妨改写为:


$E{in}$的$D$ 有N个点 ,$E{out}$的$D’$也有N个点,那么最多也就是$m_H(2N)$种hypothesis
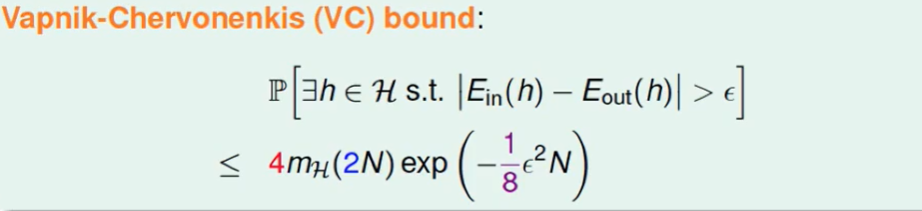
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!