CH9: Linear Regression

Linear Regression Problem(线性回归)

首先我们要知道线性回归要反映在一个具体的实数上才可以做回归，因此我们要把数据通过某种方式整合成实数。

加权计算一个分数是一种方法：

$W^T$ 是权重 ，$x$是顾客的信息，这样算出来一个加权的分数。

---

所以：

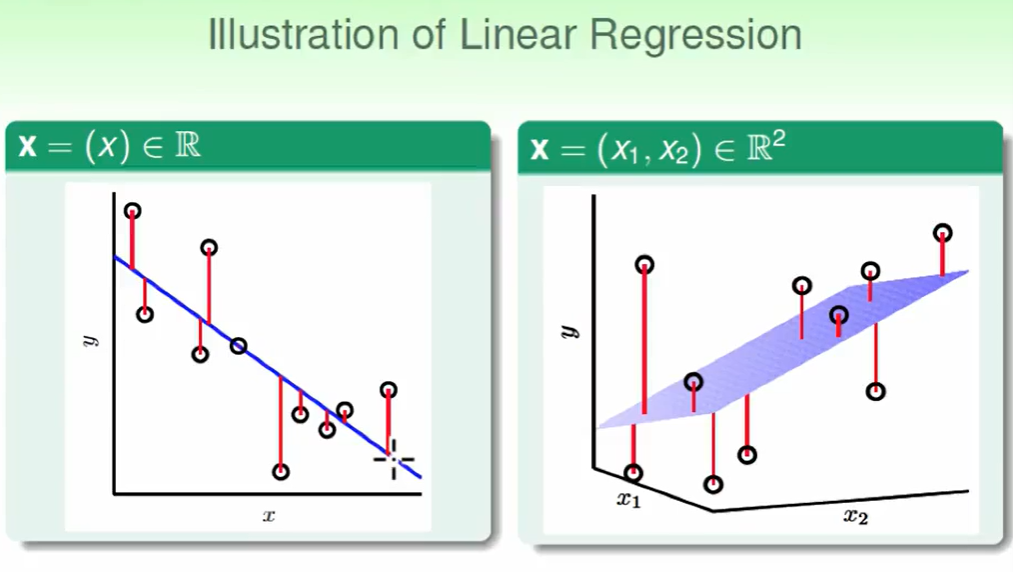
• 我们的hypothesis对于二维时，即我们找了一个$f(x)$,作为计算加权分数，然后找一条线来合适的分开这些点。

• 我们的hypothesis对于三维时，即我们找了一个$f(x_1,x_2)$,作为计算加权分数，然后找一个面来合适的分开这些点。

线性回归的问题是希望这些红色线(即余数)越小越好。

---

线性回归的错误衡量方式：

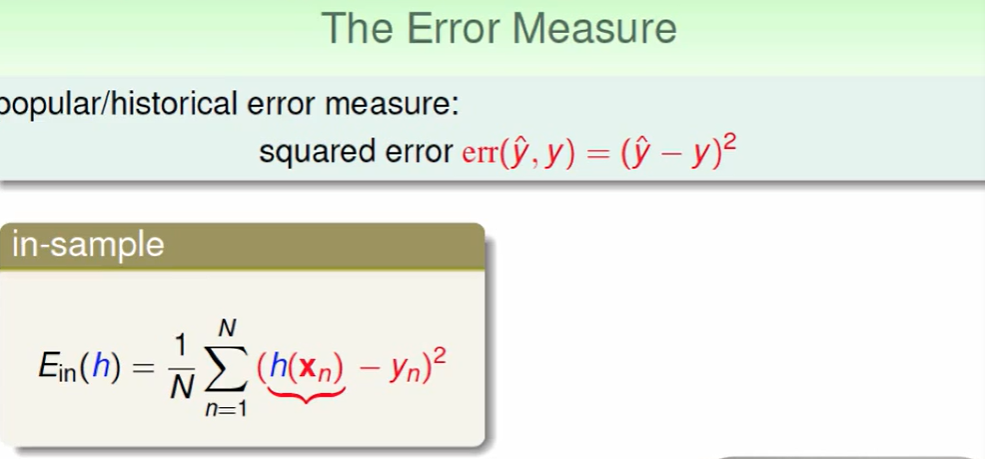
有VC Bound的理论做支撑，保证了$E{in}，E{out}$相差不大，那么下面我们的问题就是：

Linear Regression Algorithm

接着上节的这个问题开始：

首先看一下$E_{in}$的公式：

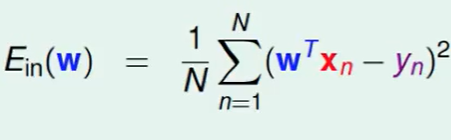
我们首先把$w^Tx_n$ 变化下顺序$x_n^Tw$,当然这个变化是很自然的，并不会改变结果。

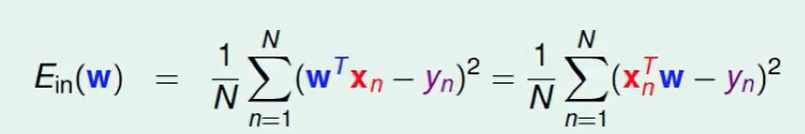
接下来我们把$\Sigma$去掉：

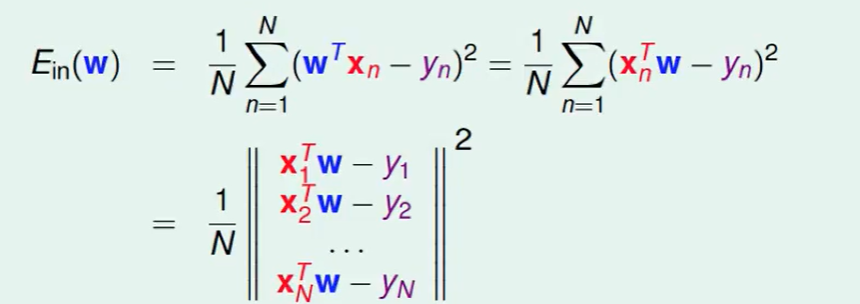
easily, 这个矩阵可以拆成下面这个东西：

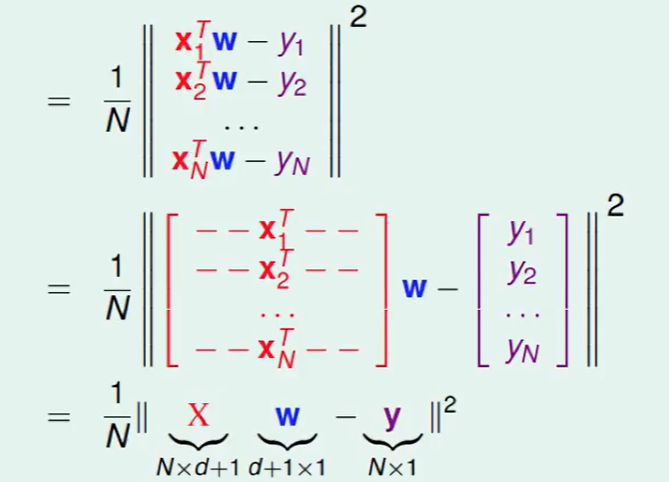
接下来的任务就是：

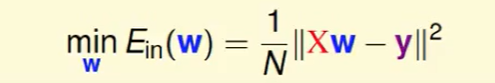
这个w和y都是确定的，w是不确定的。

画出$E_{in}$随变换的曲线：

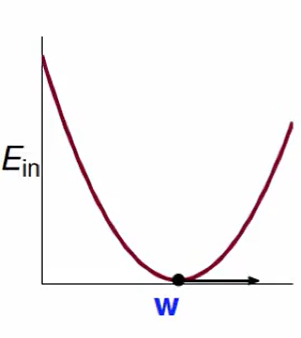
• 这是一个凸函数

• 我们在最低点取梯度，梯度是0，即

  

所以任务变成了：

---

我们把平方展开：

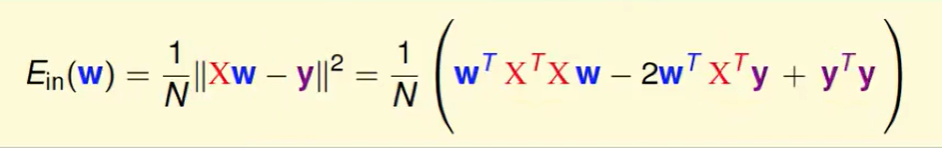
我们设一些变量：

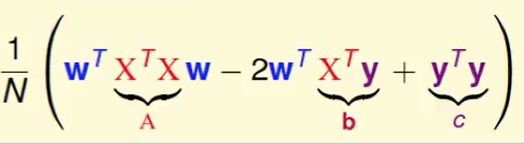
其中：

• A是矩阵
• b是向量
• c是阐述

接下来就是对向量求导：

首先我们考虑这样一个简单问题：

这个求导是非常简单。

那我们再看我们要求的东西：

我们发现这两个是很类似的。

因此我们得出梯度的表达式：

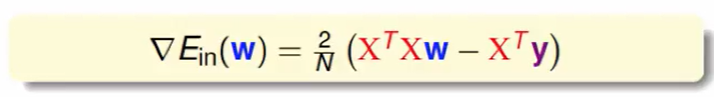
因此如果$X^TX$可逆，那么很简单：

这里有个习惯，我们把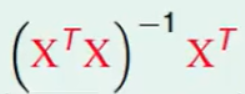这个称之为pseudo-inverse伪逆矩阵。

当然，大部分情况这个$X^TX$都是可逆的，因为 $X^TX$ 是(d+1)*(d+1)维的

当没有逆矩阵时：

因此我们如果编程语言里有 pseudo-inverse伪逆矩阵，直接用就好了。

---

最后总结一下算法：

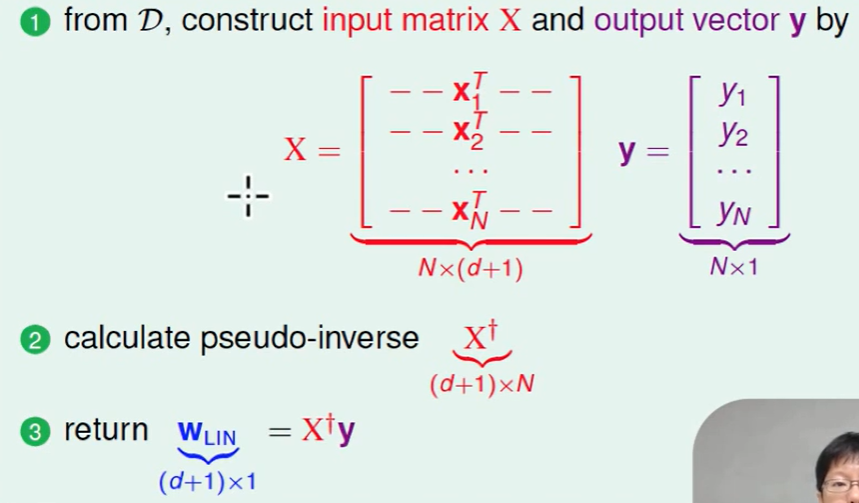
Generalization Issue

$E_{in}$的计算：

​ 我们一般把$XX^十$ 叫做hat matrix，因为它让y带上了hat，即这个东西乘上y，就是预测的y。

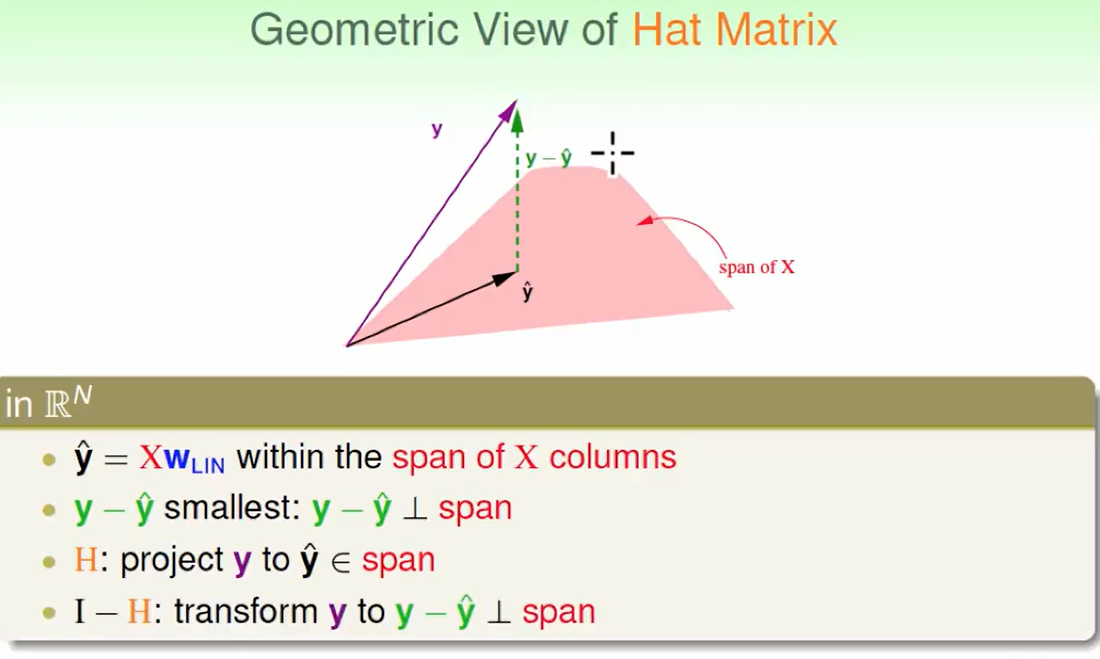
这个Hay Matrix在做什么？

• 首先我们可以看出$y\ hat$, 就是$X$列向量所张成的空间里的一个向量。

• 我们希望$y - y \ hat$尽可能小，而$y - y \ hat$ 最小肯定是垂直于span，所以这个几何意义是垂直于span的向量。

• H使得取到的最小，所以H干了一件怎么样的事情？ 是的，H把向量y投影到span上形成y hat。

那么如果有噪声的情况呢？

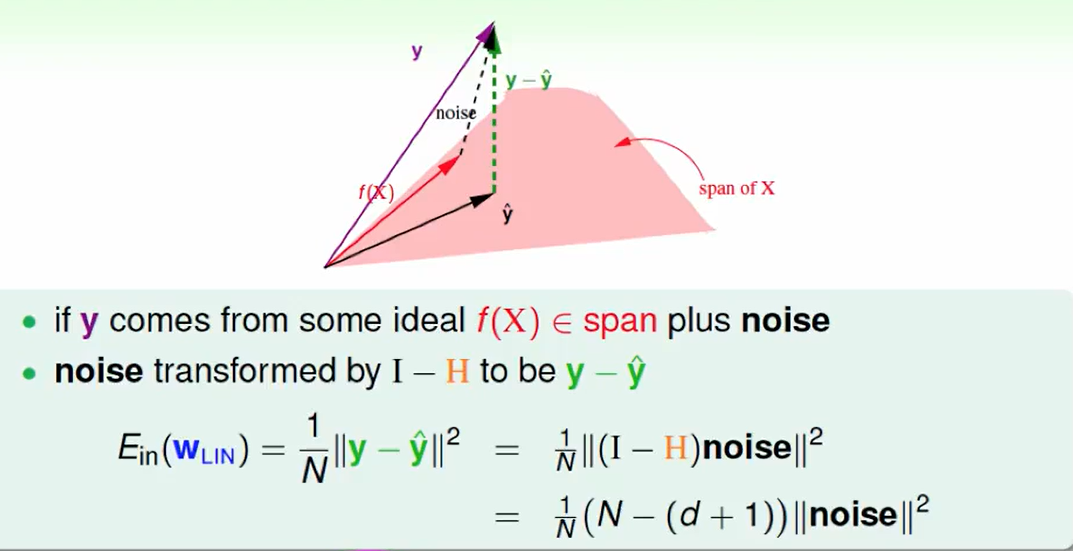
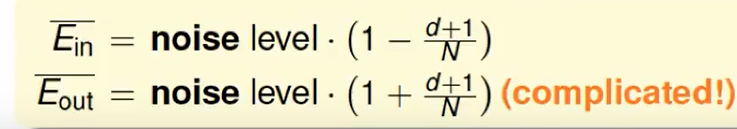
我们可以算出这两个表达式：

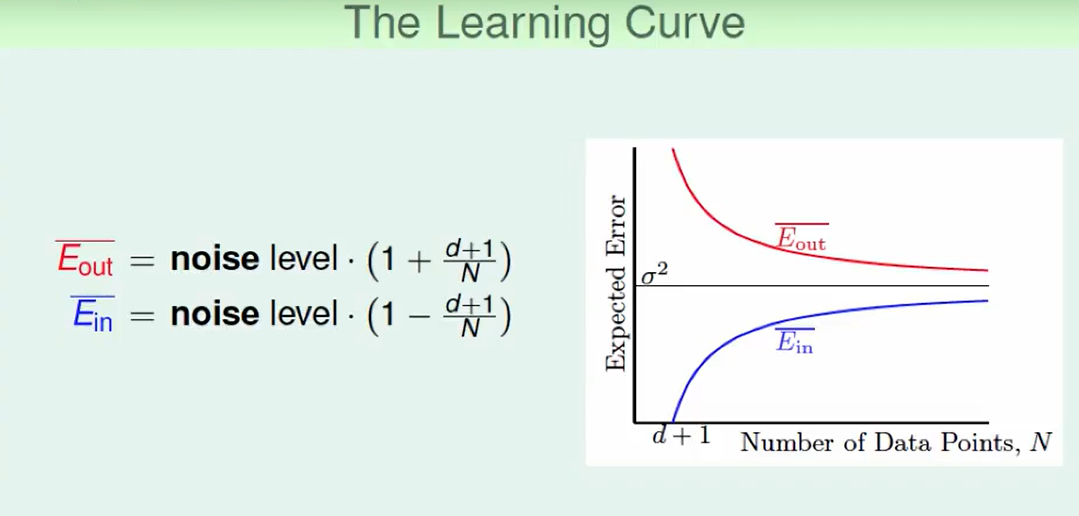
for Binary Classification

线性分类和线性回归的区别：

可是我们发现${+1,-1}∈R$，那么是不是可以不用PLA做Linear Classification，而用Linear Regression做呢？这样做的话运行就会很快了。

我们先观察一下两种错误衡量方法：

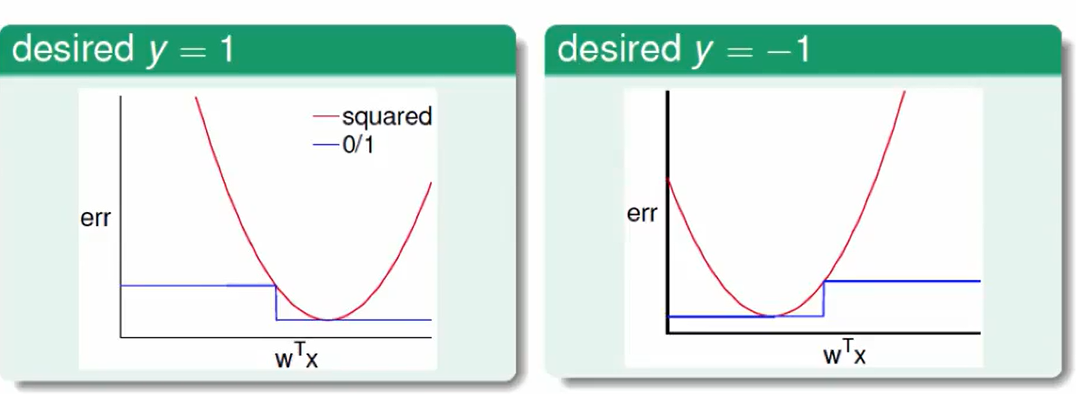
画图后我们不难发现：

配合VC Bound可以发现

这么一看 classification的Eout会被regression的Ein和根号项所包围住。

我们把红色的做好，那么蓝色的效果也不错，所以我们就是损失了一些精度来加快了速度。

因此这种替换方式是可以的。

其实我们可以组合两者的优势：

先用regression来找一个向量，作为一开始的PLA的第一个向量，然后再PLA迭代，也可以大大减少迭代。