CH11：Linear Models for Classification

Binary Classification

我们回顾一下线性模型：

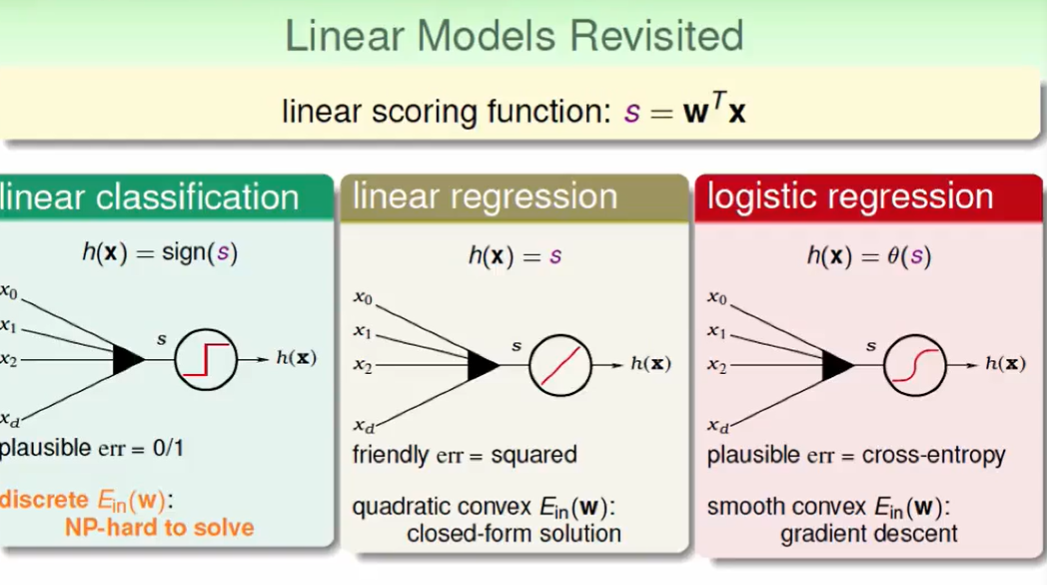
我们看一下三个error function在做classification时的区别：

$ys$代表着正确的分数。

下面我们画个图来看一下3个error function的图像：

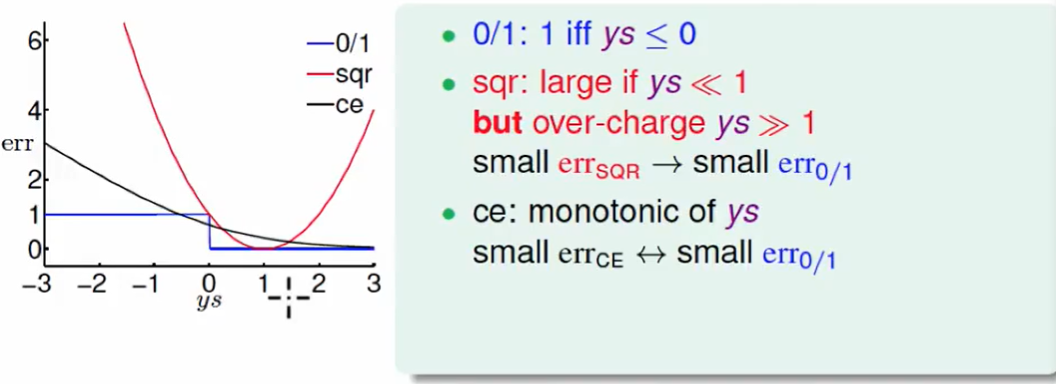
这个cross-entropy可以稍微移动下，移动到ys=0的那个阶梯直角处。

此时我们称之为 scaled cross entropy：（把取ln改为取log2）

这么做会让我们的推导容易一些。

我们来证明一下这个事情，用换底公式不难得到：

我们从VC Bound不难得知：

我们话可以用

直接得出：

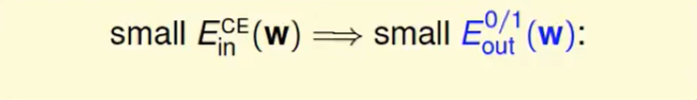
注：上述式子的提出可能会有疑问，之前不是讲得是

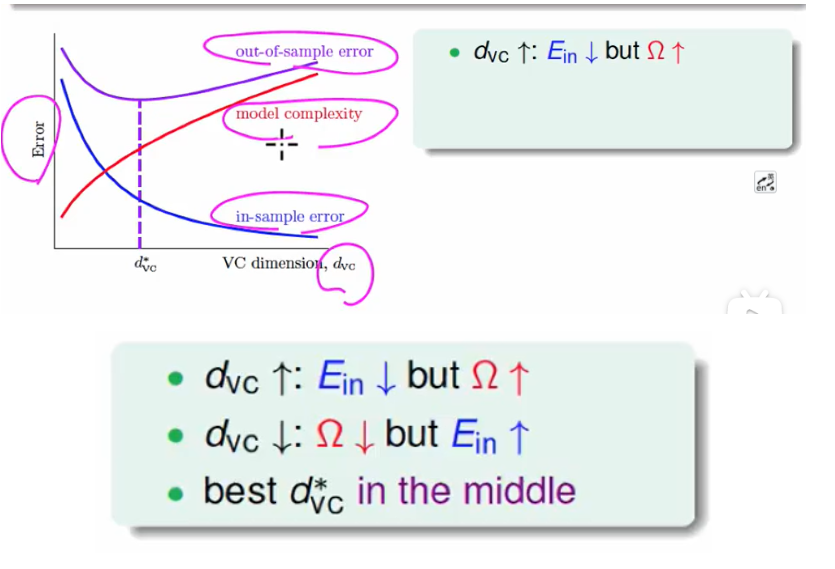
单一的让$E{in}$小并不合理,应该找一个合适的不是吗？但我们不难发现这里面说的是$d{VC}$,而我们这里要调的是$w$。

所以这里我们做完逻辑回归或者线性回归后，传回去的值要加一个sign()即可。

我们最后总结一下这三个方法的优劣：

• 用PLA时，要线性可分，若不是线性可分，那就要跑pocket
• 用linear regression时，因为有闭式解，很容易算出w，但是会lose bound（毕竟衡量错误不准确，比一般的0/1 error measure的值全都大）。
• logistic regression同理，gradient descent很容易找到一个最优解，但是也会lose bound

我们可以通过组合的方法找出一个比较好用的解，比如：

还有一点，logistic regression用得一般比pocket用的多，这是因为logistic regression的最优化性质比较好用一些。

Stochastic Grad. Descent（随机梯度下降）

这两种方式每轮迭代的速度是不一样的一个时O(1)一个是O(N)

我们想用一个随机平均代替连加，这样复杂度就会降下来。

我们可以把这样一个随机梯度理解为，实际的梯度+平均为0的噪声

但是我们经理足够多轮的更新后，还是会非常接近真正的梯度的。

我们来对比一下 ，SGD中是错了多少，而PLA中是有没有错误。

因此我们一般说SGD logistic regression ≈ soft PLA

但是问题是，SGD跑到什么时候结束呢？SGD跑到谷底是很难的

• 一般是跑足够多轮
• 学习率一般选0.1，如果x的范围不是特别离谱

Multiclass via logistic

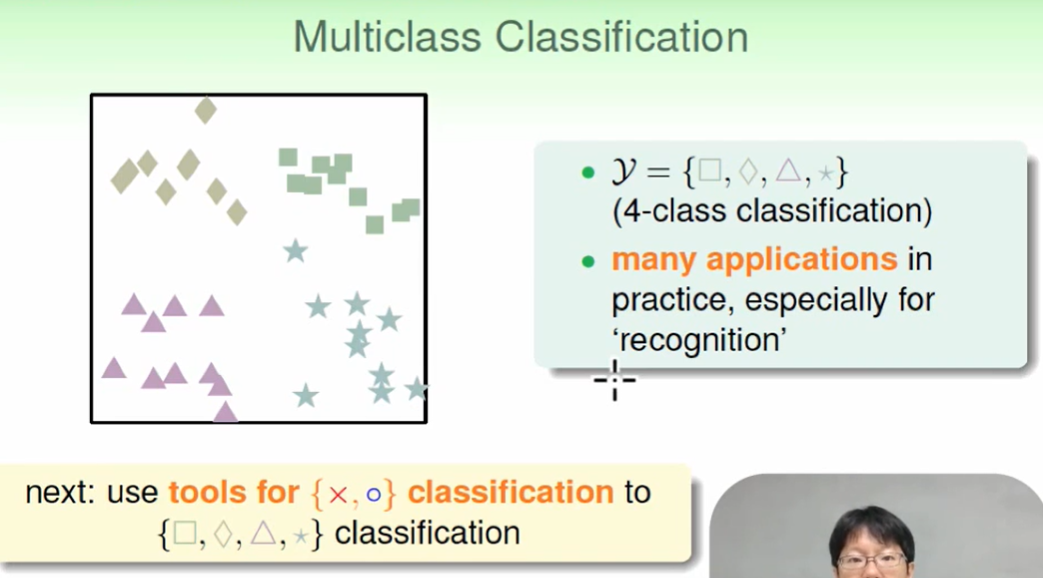
我们可以一次只做一种：

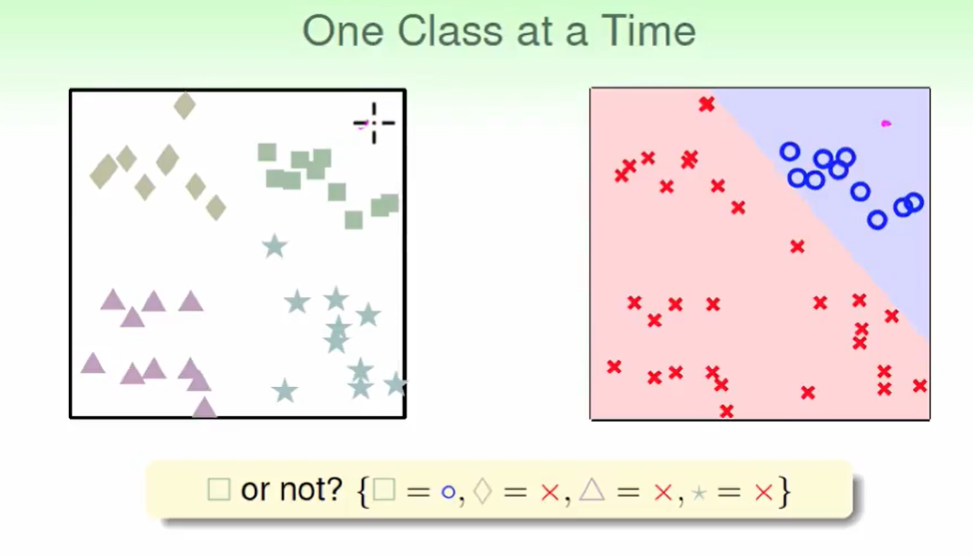
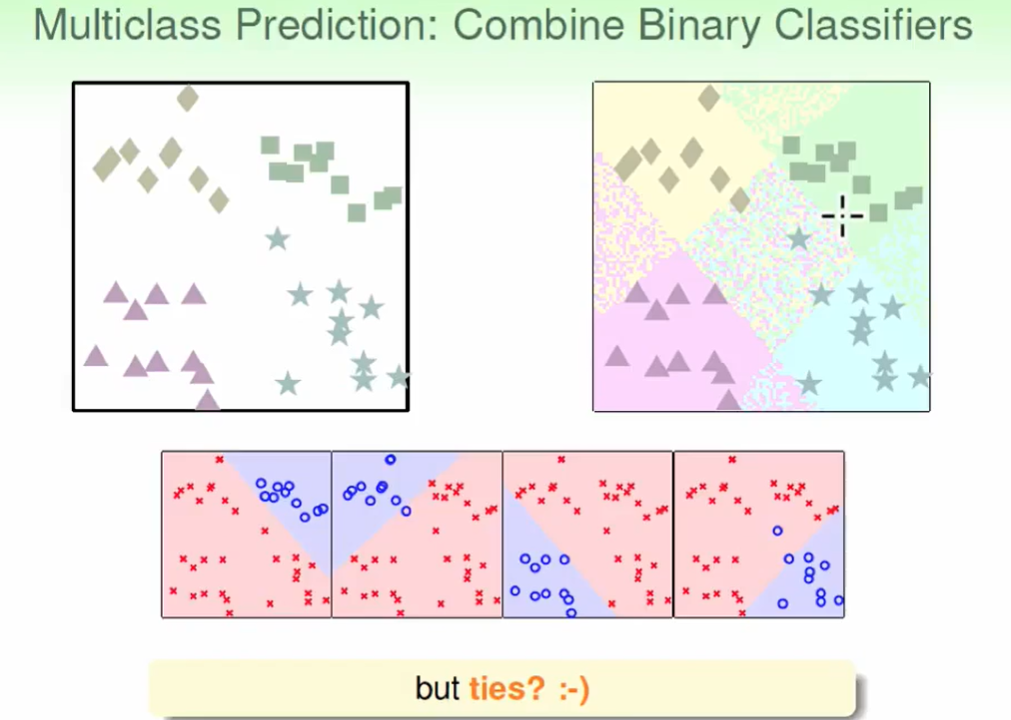
但是在

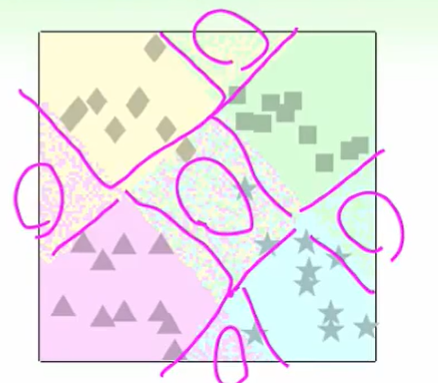
这几个地方会出现都不是四个类别或者属于多个类别的情况。

那么我们可以作soft classification，告诉我是这个类的概率。

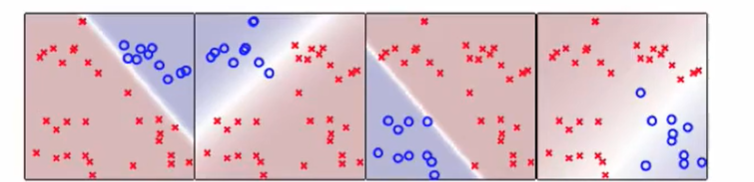
明暗代表概率，我们取最高概率作为划分：

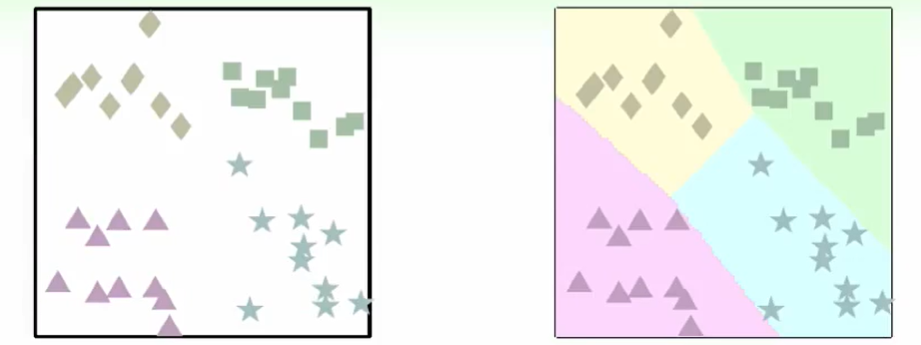
我们上面用的算法称为：

One-Versus-All(OVA) Decomposition:

这个算法的特点：

• 很高效
• 当数据量特别大时，可能会造成不平等的问题，比如100类，我们做one versus all的时候就会有99类都当作叉叉，那么会导致分类器直接全当做叉叉就好了。

Multiclass via Binary

刚才说到了 one versus all的不平等问题，纳闷我们可以考虑一半一半的分：

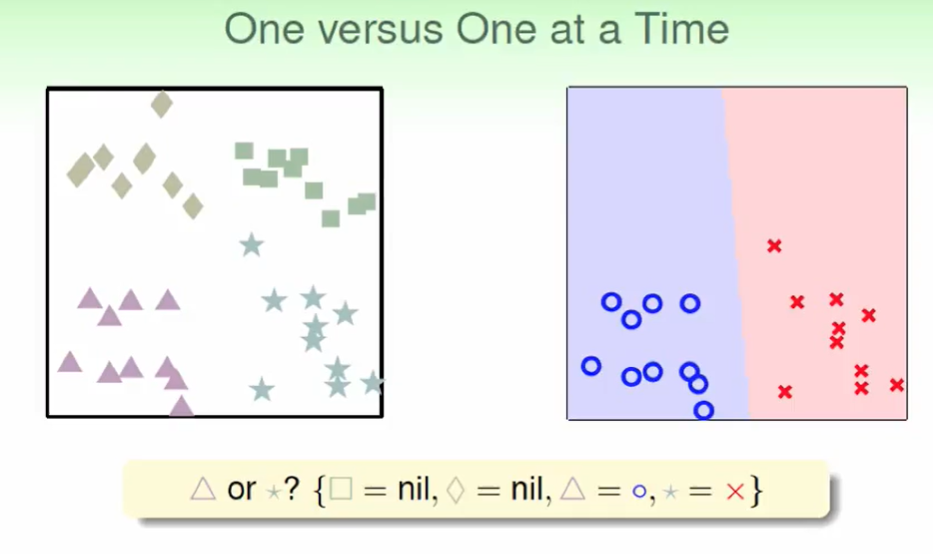
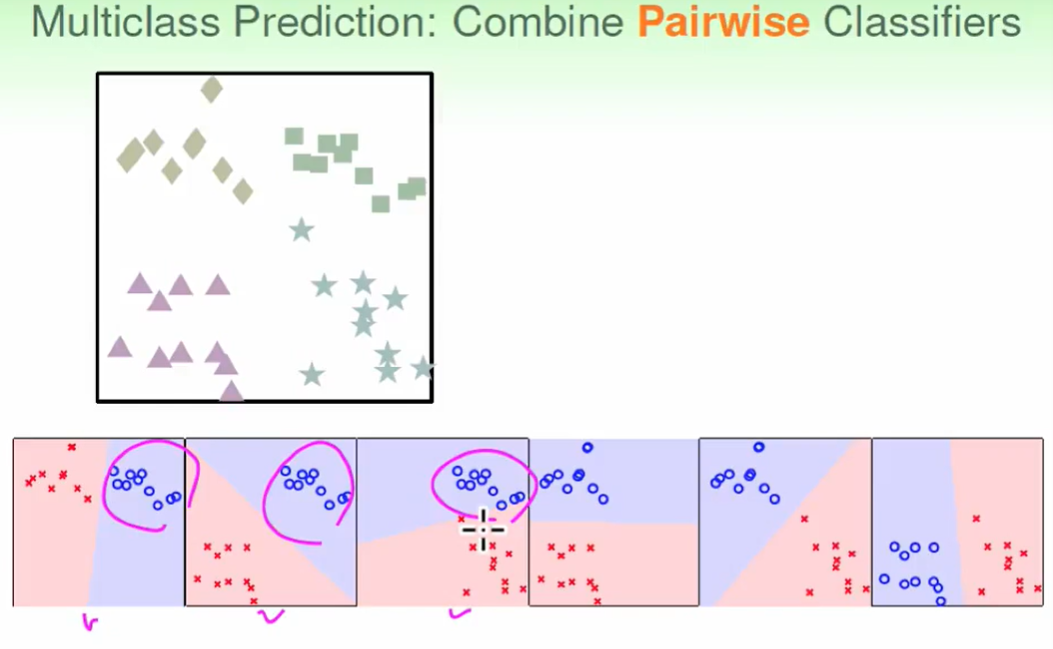
我们选两种作为圈圈，有上面六种方式。

我们发现包括方块的有前三个圈圈都包括方块

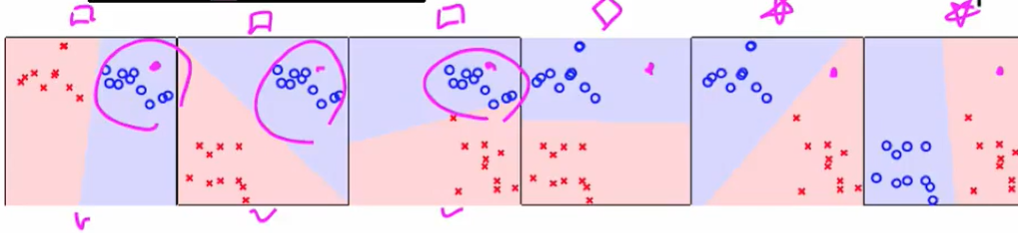
这样我们按比例就可以化作方块区域,其他同理即可以做出:

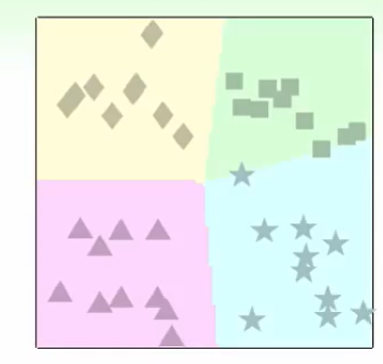
这个算法称为：

one-versus-one（OVO） Decomposition：

• 好处还是很快
• 坏处就是 比起OVA 花的时间更多，需要的空间更多。