CH4：Soft-Margin Support Vector Machine

Motivation and Primal

我们不能一直追求全部正确，数据也不一定可分。

在pocket中我们选择容忍一些错误：

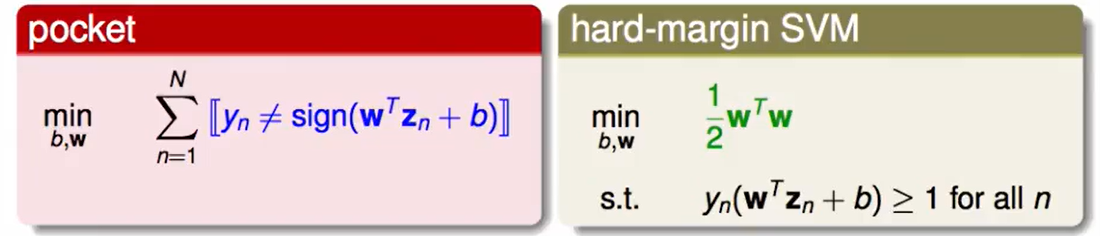
​ 因此我们让SVM上min的目标不仅包含$\frac{1}{2}w^Tw$ ,也包括错误的数量，这个C代表着这两者的权衡，如果你不在意多错一点，想要使得$\frac{1}{2}w^Tw$最小(即胖胖的间隔更宽)，那么C就可以小一点，反之同理。

​ 这是又一个trade-off： 在更宽的边界和噪声容忍度上的权衡。

上面这个式子想法很好，但是有几个问题：

• $[·]$不是一个线性函数，QP(二次规划)没法解决。
• 我们无法区分错误的严重程度，大的错误和小的错误被认为相同。

我们首先把不同的错误程度用$\xi$代表，这样我们就把记录错误的数量转换为了记录多大的错误。

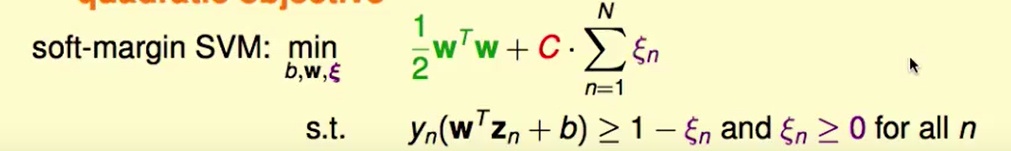
这个$\xi$代表着错误程度，如下图代表着距离胖胖额外边界的长度：

C大小的意义：

现在的问题转化为了：

有了这个以后我们做对偶的QP问题，把$\tilde{d}$拿掉。

Dual Problem

和之前一样，先求lagrange fuction：

化简一下$\xi$和$\beta$。

和之前算Dual SVM一样，对不同变量进行求偏导：

最后我们转化为了如下的问题：

这里的soft margin推导和我们之前所提到的hard margin区别就是：$\alpha$多了一个上界。

Messages

和我们做hard-margin的过程一样，但是这个里的b怎么求呢？

• 和之前hard-margin只用第一个条件，那么我们求出来的SV:终于有b和$\xi$两个未知的是无法求出b的。
• 我们考虑用第二个式子，当$\alpha<C$的时候，$\xi=0$，那么我们就可以求出解了：

用free SV可以求出$b$。

---

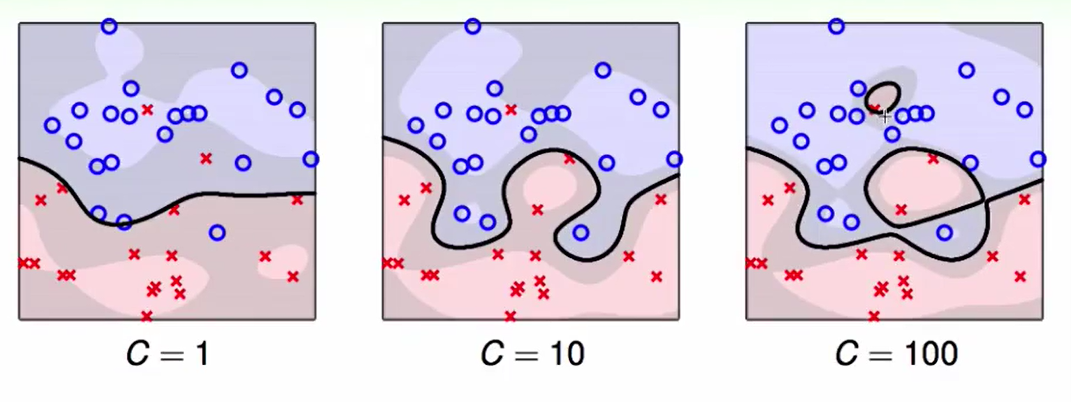
C越来越大，我们做的正确的会越来越多，但是边界会越来越瘦。

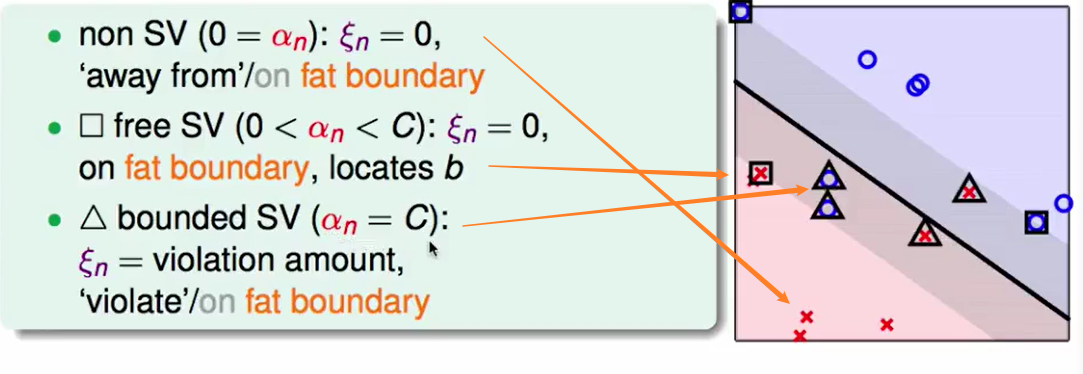
• 不是支持向量的：原理fat boundary的那些点

• free SV：fat boundary的边界点

• bounded SV：越界的点，比如：

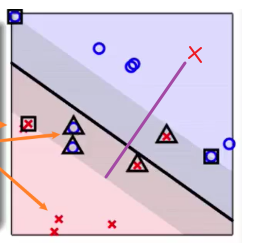
  上图中红叉的距离没有在红色边界的一遍，他的错误程度就是紫色线的距离。

Model Selection

我们在用Gauss核的时候有两个要选的：$C$和$\gamma$

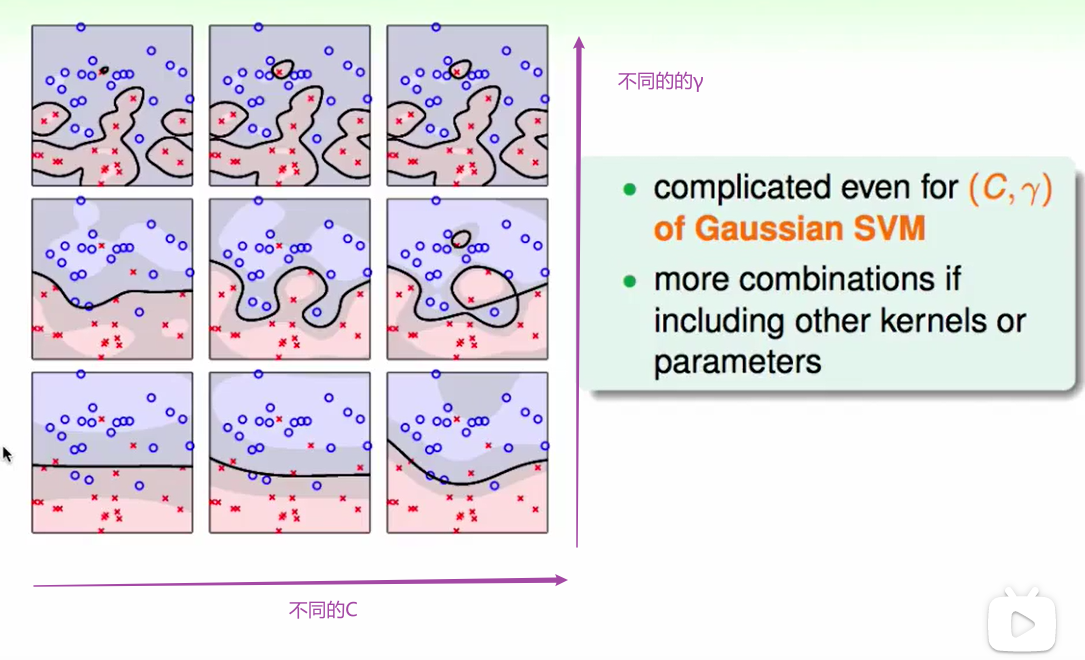
怎么选择合适的呢？

做validation即可：

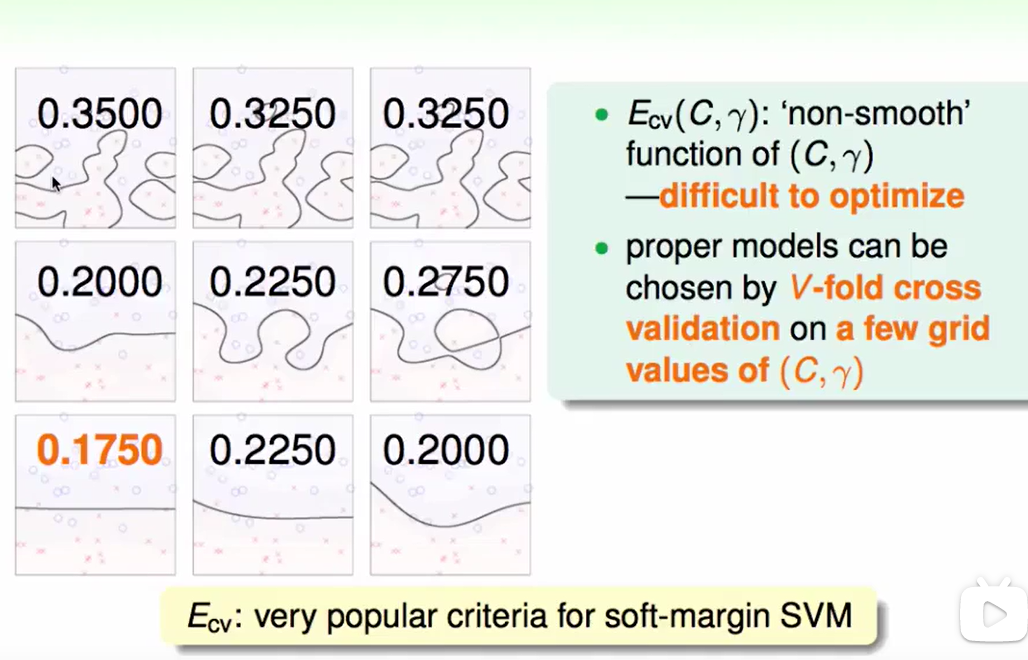
有趣的是在做Leave-One-Out Cross Validation的时候有一些新的值得注意的东西：

我们取出来的One是$\alpha=0$的，即non SV ，这些不是支持向量，因此加上也不会使得结果更准确。

我们的non-SV 一定都是正确的，而SV的错误率最多也就是1而已。加入我们一共有N个向量，那么我们同体的错误肯定小于$SV的数量 / N$.

即：

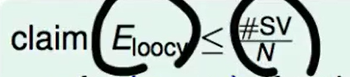
这也侧面告诉我们可以通过SV的数量来做安全检查：

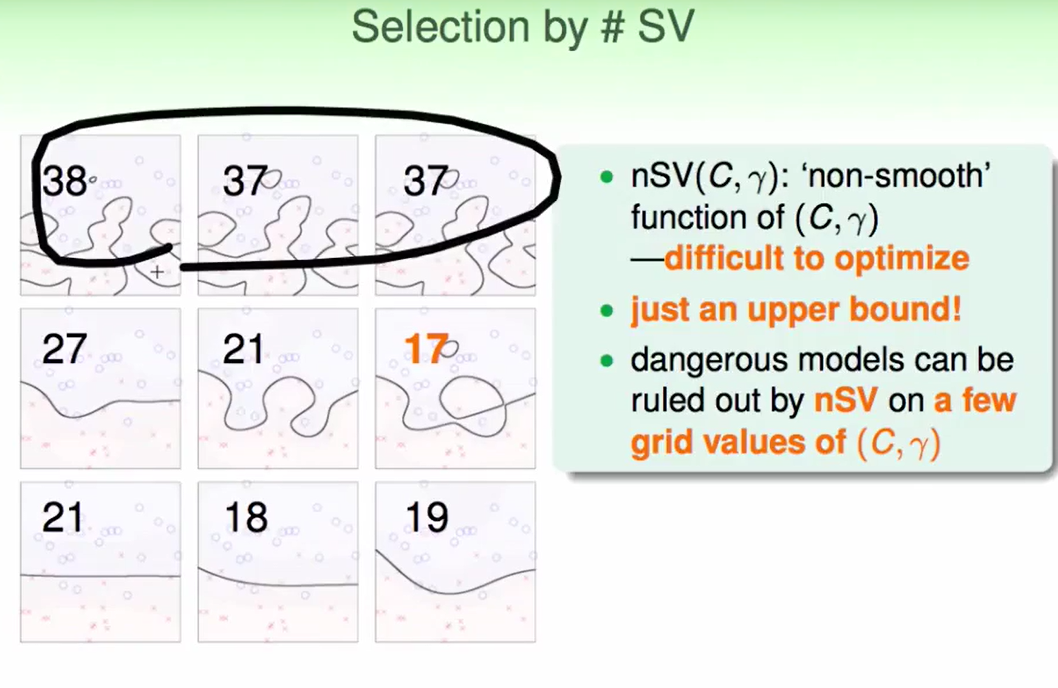
特别大的SV数量我们就要小心用了。