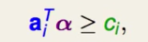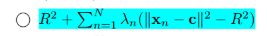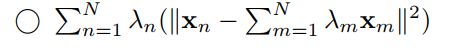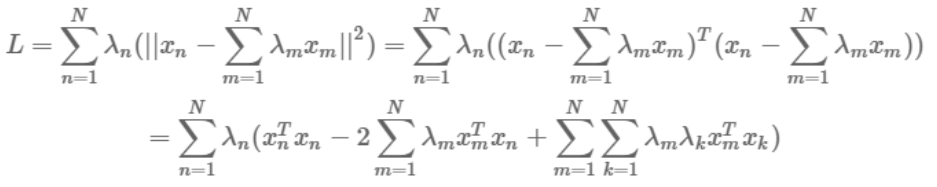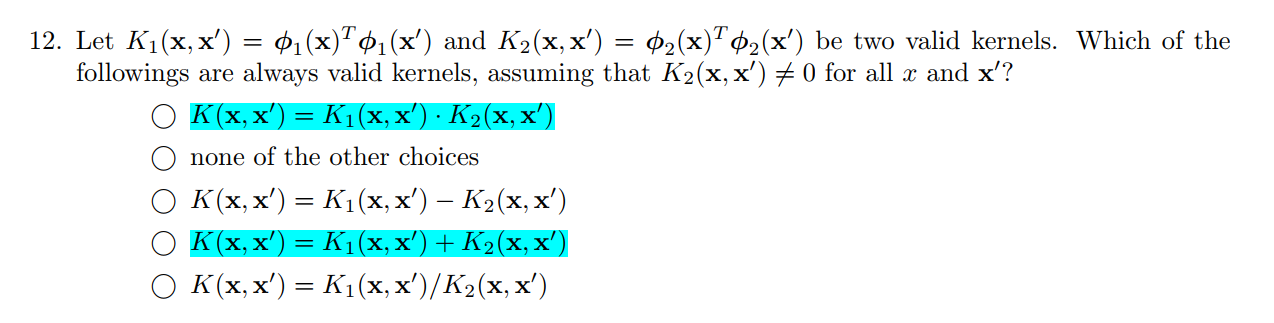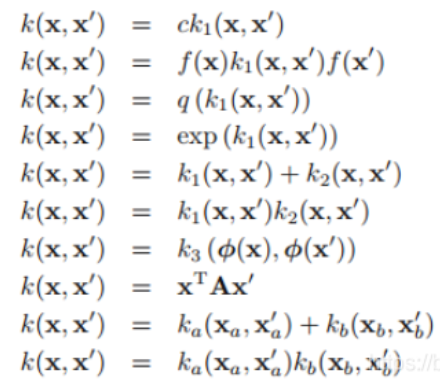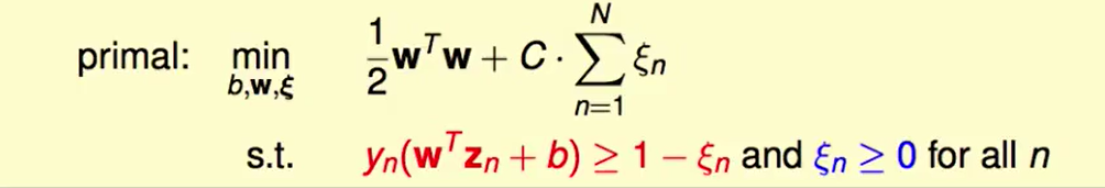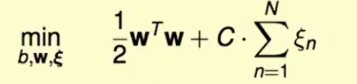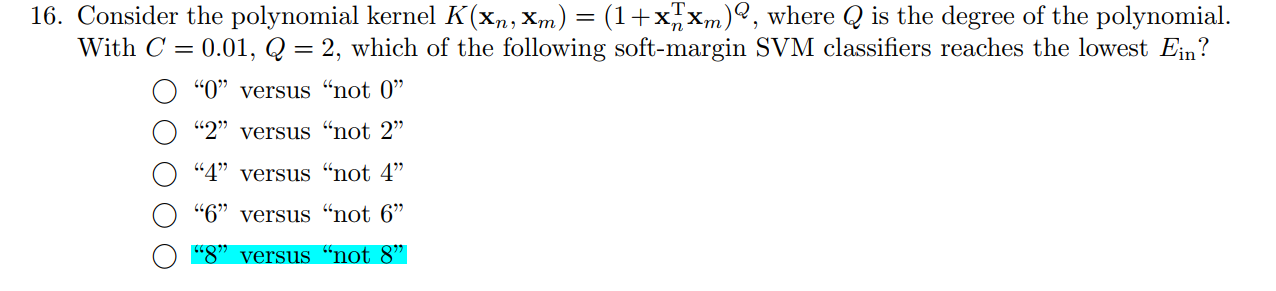机器学习技法Quiz1(homework+code)

QUIZ 1:

Q1

image-20210208171228244

Q2

image-20210208171244423

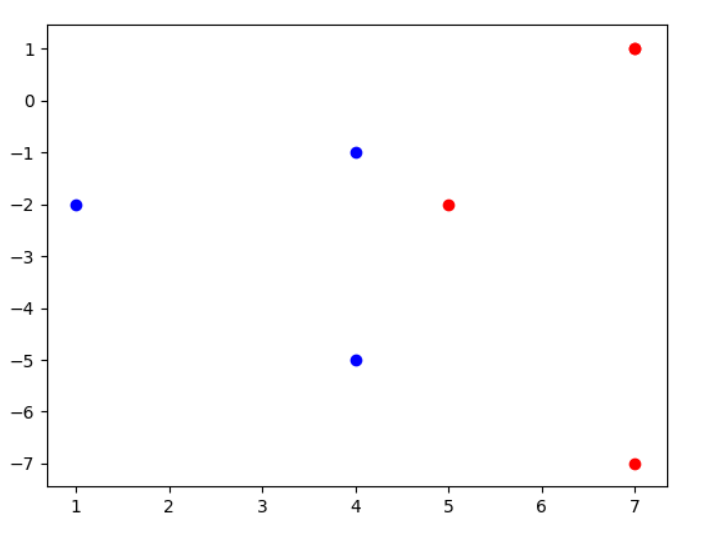
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from cvxopt import solvers, matrix
import numpy as np
import matplotlib.pyplot as plt

def z1(x1,x2):
    return x2**2 - 2*x1 + 3

def z2(x1,x2):
    return x1**2 - 2*x2 - 3

if __name__ == '__main__':
    x = np.asarray([[1, 0], [0, 1], [0, -1], [-1, 0], [0, 2], [0, -2], [-2, 0]])
    y = [-1, -1, -1, 1, 1, 1, 1]
    z = []
    for vec in x:
        z.append([z1(vec[0], vec[1]), z2(vec[0], vec[1])])
    for i in range(len(y)):
        if y[i] == -1:
            plt.scatter(z[i][0], z[i][1], color='blue')
        else:
            plt.scatter(z[i][0], z[i][1], color='red')
    plt.show()

image-20210208171255884

不难看出是在$z_1=4.5$处为分界面

Q3

image-20210208200355862

image-20210208173247333

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
from cvxopt import solvers, matrix
import numpy as np
import matplotlib.pyplot as plt

def kernel(x1, x2):
    return (1 + np.dot(x1.T, x2))**2

if __name__ == '__main__':
    x = np.array([[1, 0], [0, 1], [0, -1], [-1, 0], [0, 2], [0, -2], [-2, 0]])
    y = np.array([-1, -1, -1, 1, 1, 1, 1])
    Q = np.zeros((7, 7))
    for i in range(7):
        for j in range(7):
            Q[i][j] = y[i] * y[j] * kernel(x[i], x[j])
    P = -np.ones(7)
    A = np.zeros((9, 7))
    A[0] = y
    A[1] = -y
    for i in range(2,9):
        A[i][i-2] = -1
    C = np.zeros(9)

    Q = matrix(Q)
    P = matrix(P)
    A = matrix(A)
    C = matrix(C)

    alphas = solvers.qp(Q, P, A, C)
    print('max alpha:', np.max(alphas['x']))
    print('alpha sum:', np.sum(alphas['x']))
    print('min alpha:', np.min(alphas['x']))
    print('alphas:', alphas['x'])

这里要注意下：cvxopt做二次规划和林轩田老师ppt上的

image-20210208200148937

符号方向是相反的。

运行结果：

1
2
3
4
5
6
7
8
9
10
max alpha: 0.8888888987735439
alpha sum: 2.814814850082614
min alpha: 6.390795094251015e-10
alphas: [ 6.69e-09]
[ 7.04e-01]
[ 7.04e-01]
[ 8.89e-01]
[ 2.59e-01]
[ 2.59e-01]
[ 6.39e-10]

故1，2是正确的。

Q4

image-20210208205053236

我们已知道$\alpha$，去求b即可，然后带回$g_{SVM}$.

image-20210208204936807

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
from cvxopt import solvers, matrix
import numpy as np
import matplotlib.pyplot as plt

def kernel(x1, x2):
    return (1 + np.dot(x1.T, x2))**2

if __name__ == '__main__':
    x = np.array([[1, 0], [0, 1], [0, -1], [-1, 0], [0, 2], [0, -2], [-2, 0]])
    y = np.array([-1, -1, -1, 1, 1, 1, 1])
    Q = np.zeros((7, 7))
    for i in range(7):
        for j in range(7):
            Q[i][j] = y[i] * y[j] * kernel(x[i], x[j])
    P = -np.ones(7)
    A = np.zeros((9, 7))
    A[0] = y
    A[1] = -y
    for i in range(2,9):
        A[i][i-2] = -1
    C = np.zeros(9)

    Q = matrix(Q)
    P = matrix(P)
    A = matrix(A)
    C = matrix(C)

    alphas = solvers.qp(Q, P, A, C)
    alphas = alphas['x']

    def kernelParameters(x):
        return np.array([x[0] * x[0], x[1] * x[1], 2 * x[0] * x[1], 2 * x[0], 2 * x[1], 1])

    w = np.zeros(6)
    for i in range(7):
        w += alphas[i] * y[i] * kernelParameters(x[i])

    b = y[1]
    for i in range(7):
        b = b - alphas[i] * y[i] * kernel(x[i], x[1])

    print('x1*x1:', w[0], 'x2*x2:', w[1], 'x1*x2:', w[2], 'x1:', w[3], 'x2:', w[4], '1:', w[5])
    print('b:', b)

运行结果：

1
2
x1*x1: 0.8888888946403547 x2*x2: 0.666666683766254 x1*x2: 0.0 x1: -1.7777778134824205 x2: -3.3306690738754696e-15 1: -1.586721330977244e-10
b: -1.6666666836075785

即第三个。

Q5

image-20210208205446378

Q6

image-20210208210536028

image-20210208210408313

根据上面的ppt用lagrange multiplier转化为lagrange function即可：

要注意的是 ppt里给的是$\ge$, 而题目里是$\le$, 两边同加上负号，让符号方向就会转回来即可。

答案是第一个。

Q7

image-20210208221238672

我们仿写KKT条件：

$\frac{\partial L(R,c,\lambda)}{\partial R}= R(1-\Sigma_{n=1}^N \lambda_n)=0$

$\frac{\partial L(R,c,\lambda)}{\partial ci}=0 \to c_i\Sigma{n=1}^N\lambdan =\Sigma{n=1}^N\lambda_nx_n^{(i)} $

这样就推出了第1，3个是正确的。

然后为来看第五个，就是KKT条件中所提到的：

img

我们仿写就是：$\lambda_n(||x_n-c||^2-R^2) = 0$

那么第5个也正确。

所以答案是1，3，5。

Q8

1

解析：

题目提到$R>0$，由Q7可知：$R(1-\Sigma{n=1}^N \lambda_n)=0$,故$1-\Sigma{n=1}^N \lambda_n=0$

原始的Lagrange Function在Q6中提到了：image-20210209010640077

我们把$1-\Sigma_{n=1}^N \lambda_n=0$带入：

$\ \ \ R^2 + \Sigma{n=1}^N\lambda_n(||x_n-c||^2-R^2)\ = R^2 + \Sigma{n=1}^N\lambdan||x_n-c||^2-\Sigma{n=1}^N\lambdanR^2 \=\Sigma{n=1}^N\lambda_n||x_n-c||^2$

我们又由Q7中的式子：

$\frac{\partial L(R,c,\lambda)}{\partial ci}=0 \to c_i\Sigma{n=1}^N\lambdan =\Sigma{n=1}^N\lambda_nx_n^{(i)} $

又因为$1-\Sigma_{n=1}^N \lambda_n=0$，得到：

$ci\Sigma{n=1}^N\lambdan =\Sigma{n=1}^N\lambdanx_n^{(i)} \\to c_i = \Sigma{n=1}^N\lambda_nx_n^{(i)}$

带入$\Sigma_{n=1}^N\lambda_n||x_n-c||^2$得到第5个为正确答案：

image-20210209011310332

Q9

image-20210209012631861

解析：

从Q8的结果加上kernel技巧就好：

image-20210209011857250

image-20210209012611033

Q10

image-20210209151933569

解析：

image-20210209151912720

选择$\lambda\ne 0 $的SV。

Q11

image-20210209163047123

image-20210209163059245

Q12

image-20210209163525843

解析：

下面这些都可以：

image-20210209163514687

Q13

image-20210209164101993

Q14

image-20210209175524211

$K(x,x’)=z^Tz $,这里把$K(x,x’)$改写为$pK(x,x’)+q$后，怎样改写$C$才能使得不影响分类效果呢？

这个是soft-margin SVM的原问题：

image-20210209175847416

我们知道用核技巧，其实就是把$x$映射到$z$空间上,而$pK(x,x’)+q$这样的改变中，$q$平移空间是不会影响结果的，而$p$拉伸空间是可以改变结果的，所以我们只考虑$p$即可。

$K$变成原来的$p$倍，那么$z$就是原来的$\sqrt{p}$倍，这样我们为了这个不变化：

image-20210209180225533

$w$就要变成原来的$\frac{1}{\sqrt{p}}$倍，那么为了使下式子不被影响到：

image-20210209180329037

由于$\frac{1}{2}w^Tw$变为了原来的$\frac{1}{p}$倍，那么C也要变为原来的$\frac{1}{p}$倍。

即答案为第五个。

Q15

image-20210209232600273

image-20210209232614619

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
from cvxopt import solvers, matrix
import numpy as np
import matplotlib.pyplot as plt
import sklearn.svm as svm
import math

def splitData(path):
    txt = open(path)
    data_y = []
    data_x = []
    for line in txt:
        linesplit = line.split()
        data_y.append(int(float(linesplit[0])))
        data_x.append([float(linesplit[1]), float(linesplit[2])])
    return np.array(data_x), np.array(data_y)


def classificationFunction(dataOfy, target):
    newdata_y = []
    for _ in dataOfy:
        if _ == target:
            newdata_y.append(1)
        else:
            newdata_y.append(0)
    return np.array(newdata_y)



if __name__ == '__main__':
    train_data_x, train_data_y = splitData("train.dat")
    train_data_y = classificationFunction(train_data_y, 0)

    clf = svm.SVC(C=0.01, kernel='linear')
    clf.fit(train_data_x, train_data_y)
    w = clf.coef_
    print(np.sqrt(np.sum(np.square(w))))
    
    #0.5713171494256942

Q16

image-20210209233841082

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
from cvxopt import solvers, matrix
import numpy as np
import matplotlib.pyplot as plt
import sklearn.svm as svm
import math

def splitData(path):
    txt = open(path)
    data_y = []
    data_x = []
    for line in txt:
        linesplit = line.split()
        data_y.append(int(float(linesplit[0])))
        data_x.append([float(linesplit[1]), float(linesplit[2])])
    return np.array(data_x), np.array(data_y)


def classificationFunction(dataOfy, target):
    newdata_y = []
    for _ in dataOfy:
        if _ == target:
            newdata_y.append(1)
        else:
            newdata_y.append(0)
    return np.array(newdata_y)



if __name__ == '__main__':
    Ein = 1
    SelectClassway = 0
    for i in range(9):
        test_data_x, test_data_y = splitData("test.dat")
        train_data_x, train_data_y = splitData("train.dat")
        train_data_y = classificationFunction(train_data_y, i)
        test_data_y = classificationFunction(test_data_y, i)
        clf = svm.SVC(C=0.01, kernel='poly', degree=2, gamma='auto')
        clf.fit(train_data_x, train_data_y)
        y_hat = clf.predict(test_data_x)
        correct_num = np.sum(y_hat == test_data_y)
        if 1 - correct_num/test_data_y.shape[0] < Ein:
            Ein = 1 - correct_num/test_data_y.shape[0]
            SelectClassway = i
    print(i)
    #8

Q17

image-20210209234211953

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
from cvxopt import solvers, matrix
import numpy as np
import matplotlib.pyplot as plt
import sklearn.svm as svm
import math

def splitData(path):
    txt = open(path)
    data_y = []
    data_x = []
    for line in txt:
        linesplit = line.split()
        data_y.append(int(float(linesplit[0])))
        data_x.append([float(linesplit[1]), float(linesplit[2])])
    return np.array(data_x), np.array(data_y)


def classificationFunction(dataOfy, target):
    newdata_y = []
    for _ in dataOfy:
        if _ == target:
            newdata_y.append(1)
        else:
            newdata_y.append(0)
    return np.array(newdata_y)



if __name__ == '__main__':
    Ein = 1
    SelectClassway = 0
    maxxalpha = 0
    for i in range(0, 9, 2):
        test_data_x, test_data_y = splitData("test.dat")
        train_data_x, train_data_y = splitData("train.dat")
        train_data_y = classificationFunction(train_data_y, i)
        test_data_y = classificationFunction(test_data_y, i)
        clf = svm.SVC(C=0.01, kernel='poly', degree=2, gamma='auto')
        clf.fit(train_data_x, train_data_y)
        y_hat = clf.predict(test_data_x)
        correct_num = np.sum(y_hat == test_data_y)
        if 1 - correct_num/test_data_y.shape[0] < Ein:
            Ein = 1 - correct_num/test_data_y.shape[0]
            SelectClassway = i
        if np.sum(np.fabs(clf.dual_coef_)) > maxxalpha:
            maxxalpha = np.sum(np.fabs(clf.dual_coef_))
    print(maxxalpha)
    #23.88

Q18

image-20210210002831071

Q19

image-20210210004623282

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
from cvxopt import solvers, matrix
import numpy as np
import matplotlib.pyplot as plt
import sklearn.svm as svm
import math

def splitData(path):
    txt = open(path)
    data_y = []
    data_x = []
    for line in txt:
        linesplit = line.split()
        data_y.append(int(float(linesplit[0])))
        data_x.append([float(linesplit[1]), float(linesplit[2])])
    return np.array(data_x), np.array(data_y)


def classificationFunction(dataOfy, target):
    newdata_y = []
    for _ in dataOfy:
        if _ == target:
            newdata_y.append(1)
        else:
            newdata_y.append(0)
    return np.array(newdata_y)



if __name__ == '__main__':
    Eout = 1
    Select = 0
    maxxalpha = 0
    for gamma in [1, 10, 100, 1000, 10000]:
        print(gamma)
        test_data_x, test_data_y = splitData("test.dat")
        train_data_x, train_data_y = splitData("train.dat")
        train_data_y = classificationFunction(train_data_y, 0)
        test_data_y = classificationFunction(test_data_y, 0)
        clf = svm.SVC(C=0.1, kernel='rbf', gamma=gamma)
        clf.fit(train_data_x, train_data_y)
        y_hat = clf.predict(test_data_x)
        correct_num = np.sum(y_hat == test_data_y)
        if 1 - correct_num/test_data_y.shape[0] < Eout:
            Eout = 1 - correct_num/test_data_y.shape[0]
            Select = gamma
    print(Select)
    #10

Q20

image-20210210010309503

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
from cvxopt import solvers, matrix
import numpy as np
import matplotlib.pyplot as plt
import sklearn.svm as svm
import math
import random

def splitData(path):
    txt = open(path)
    data_y = []
    data_x = []
    data = []
    for line in txt:
        linesplit = line.split()
        data.append([int(float(linesplit[0])), float(linesplit[1]), float(linesplit[2])])
    random.shuffle(data)

    for line in data:
        linesplit = line
        data_y.append(int(float(linesplit[0])))
        data_x.append([float(linesplit[1]), float(linesplit[2])])
    return np.array(data_x), np.array(data_y)


def classificationFunction(dataOfy, target):
    newdata_y = []
    for _ in dataOfy:
        if _ == target:
            newdata_y.append(1)
        else:
            newdata_y.append(0)
    return np.array(newdata_y)



if __name__ == '__main__':
    g = {1: 0, 10: 0, 100: 0, 1000: 0, 10000: 0}
    for _ in range(100):
        Eout = 1
        Select = 0
        for gamma in [1, 10, 100, 1000, 10000]:
            train_data_x, train_data_y = splitData("train.dat")
            train_data_y = classificationFunction(train_data_y, 0)
            clf = svm.SVC(C=0.1, kernel='rbf', gamma=gamma)
            clf.fit(train_data_x[0:1000], train_data_y[0:1000])
            y_hat = clf.predict(train_data_x[0:1000])
            correct_num = np.sum(y_hat == train_data_y[0:1000])
            if 1 - correct_num/1000 < Eout:
                Eout = 1 - correct_num/1000
                Select = gamma
        print(Select)
        g[Select] += 1
    print(g)
    #10
    #{1: 1, 10: 97, 100: 1, 1000: 1, 10000: 0}