CH5：Kernel Logistic Regression

Soft-Margin SVM as Regularzied

当$(x_n,y_n)$越过边界时，错误就是$1-y_n(w^Tz_n+b)$,当$(x_n,y_n)$没有越过边界时，说明他是正确的没有错误，即$\xi=0$,那么我们综上所述：可以把$\xi$换成另一种写法：$max(1-y_n(w^Tz_n+b),0)$

此时我们的SVM可以这么写:

这样一来，我们把之前抽象的$\xi$概念转化为了具体的式子，同时我们现在可以通过 $b,w$的不同取值最小化下式的soft-margin SVM问题：

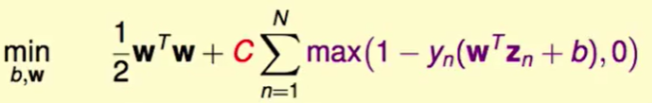
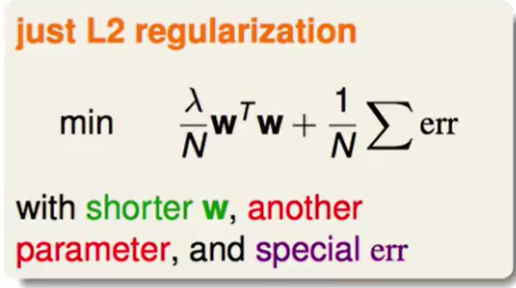
因此soft-margin SVM就是一个L2 regularization的问题。

他们之间有一些相互的关系：

SVM versus Logistic Regression

首先我们对比一下0-1error 和 SVM中的error measure的区别：

不难看出：SVM中的error measure总是大于0-1error measure。

之前在logistic regression中所用到的error measure方法叫做：scaled cross-entropy error ，详细推导见：logistic regression。

首先有个概念叫做：cross entropy

但是为了图像对比，改进成了scaled cross-entropy,即$ln$换成了$log_2$

我们对比一下三者：

这样看来： SVM的error measure方法和logistic regression的error measure方法很相似。

SVM此时可以看作: 有着L2-regularized的logistic regression

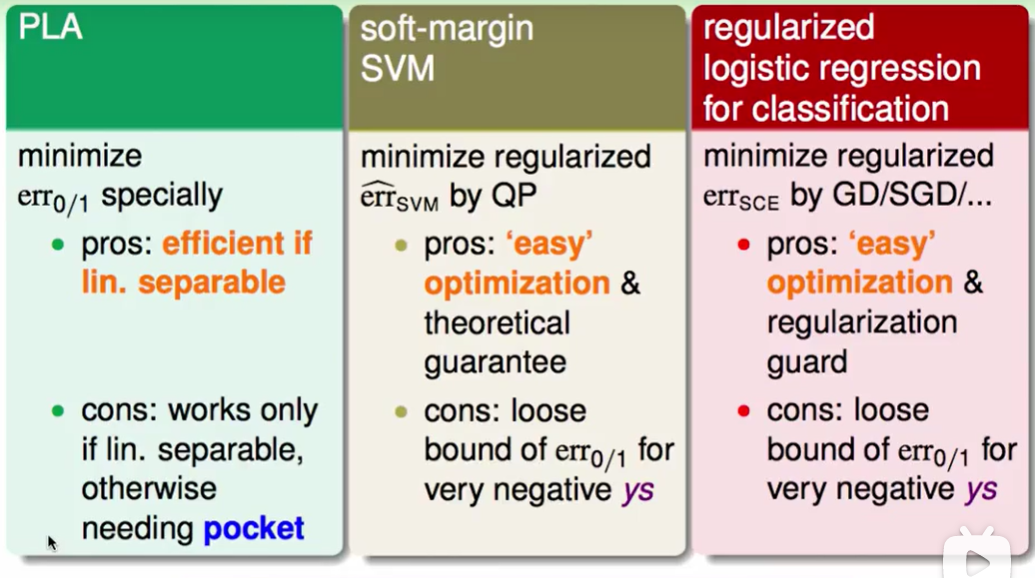
因此现在我们有了一个新的想法：

当我们求出SVM的解的时候，我们是否可以通过SVM的解来反映logistics regression里的几率问题呢？

SVM for Soft Binary

• 我们跑soft-margin SVM然后得到$b，w$, 然后传回到g(x)当作分类器，相当于是利用了SVM来直接算出Logistic regression问题。这样的方法表现得一般不错，但是少了一些逻辑回归的特点，logistics regression体现了极大似然估计相关的一些想法，且梯度下降强调的是maximum(最大)，但是现在SVM跑出来的肯定和最大有一点点的差距。

• 我们还有一种想法就是： 我们做逻辑回归时需要选一个起始点然后去做SGD/GD(梯度下降)，那么我们可以把SVM求出来的结果当作迭代的起始点，然后再去做SGD/GD。但是这样的做法会使得我们SVM中的kernel的特点没法用到，也就是遇到non-linear的情况会无法解决。

我们想着补全两者的缺点，一个想法是添加上两个自由度A,B：

• 用A,B去微调hyperplane 使得其满足maximum likelihood的特性。

• 同时我们由于保留了$\phi$,所以kernel的特点也保留了下来。

同时我们也要注意到：

A一般大于0，如果你的A小于0，说明你的$w_{SVM}$求得有问题。B一般约等于0，他只是平移hyperplane，由于我们SVM求出的已经比较准确了，所以一般不会有什么太大的动作。

那现在只需要优化这个A,B即可，用logistic regression的目标优化方程套进去即可：

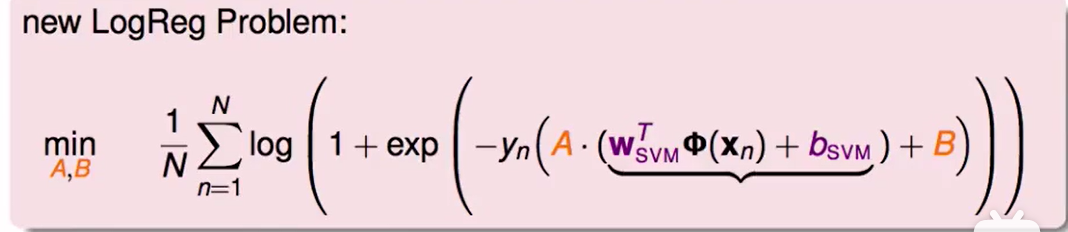
我们观察这个式子：

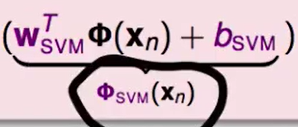
这个操作将一个多维的数据$x_n$转换为了一个具体的数:

$\phi{SVM}(x_n)=w{SVM}^T\phi(xn)+b{SVM}$

我们再用这个值作为训练数据来用A,B做调整即可，此时logistics regression此时只需要做A,B两个维度即可。

其实Platt Model种提出的Probablistic SVM和这个很相似，只不过多了一些正则化，我们这里不讲platt提出的这些细节。

但是这样得到的不是Z空间的最优解，只是一个经过A,B调整后比较好的解。

Kernel Logistic Regression

最优解的$w$中也包含核技巧，并且也是$z_n$的线性组合

其实无论是SVM，PLA还是logReg by SGD都是$z_n$的线性组合：

所以我们得出结论：

​ 我们的最佳的$w_*$一定是由两部分组成的，一部分是$z_n$所张成的空间，另一部分是垂直于这个张成的空间。

​ 我们肯定希望垂直于张成的空间的w部分，即$w⊥=0$，因为做到$w⊥=0$时说明我们最优化的$w_*$可以全部用$z_n$来表示了。

我们思考一下$w_⊥$到底会影响到什么？

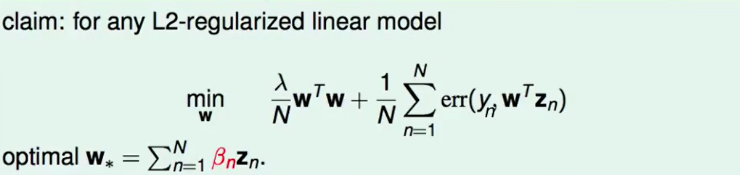
考虑目标优化函数的两部分，一部分是err() ,另一部分是$w^Tw$。

如果$w_⊥\ne 0$会得到什么结果呢？我们考虑一下下面两个部分：

• 第一部分：err()

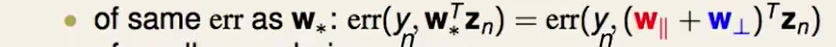
我们发现这部分并不会被影响因为$w_⊥z_n=0$是一个事实，垂直于$z_n$的向量和$z_n$相乘当然等于0。

• 第二部分：$w^Tw$

  

  当考虑$w$大小时就出现了问题，可以看出向量会大一些。但是这就出现了问题，这提示我们$w*^Tw*>w∥^Tw∥$,这说明我们的最优解不是最优解了竟然，这意味着我们的最优w中：w$w_⊥=0$是恒成立的。

$w⊥=0$是恒成立的就意味着：**我们的$w$一定是由$z_n$的线性组合得来的。*

这样一来我们就可以加上核技巧了。

此时我们求解$\beta$即可。

怎么求呢？ GD/SGD都是很好的选择。

另一种视角：

• 相当于权重$\beta$和做feature transform后的数据的乘积。

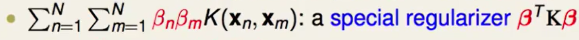• 这部分可以看作一种特殊的正则化。

• 因此Kernel Logistic Regression可以看作$\beta$的线性模型，只不过它是通过kernel transform后的数据和一种特殊的kernel regularizer 得到的结果。