CH6：Support Vector Regression

Kernel Ridge Regression

如上一节所说，我们可以把最优解的$w_*$看作$z_n$的线性组合

因此我们可以解最优的$\beta$即可求出$w_*$.

这部分我们怎么求来的呢？

首先第一部分：

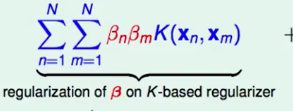
我们可以化为矩阵的形式来表达这个式子：$\beta K\beta$, 其中$\beta$是一个$1N$矩阵，$K$是一个$NN$的矩阵，其中$K_{n,m}$代表着$K(x_n,x_m)$。

第二部分：

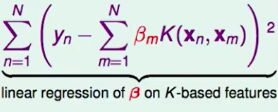
平方和我们可以看作 一个向量的内积，即：$||y_n-\beta K||^2$,两部分都带入展开即可得到下式：

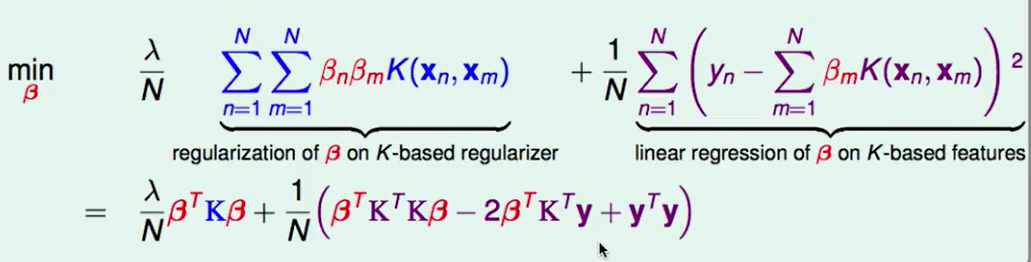
求梯度：

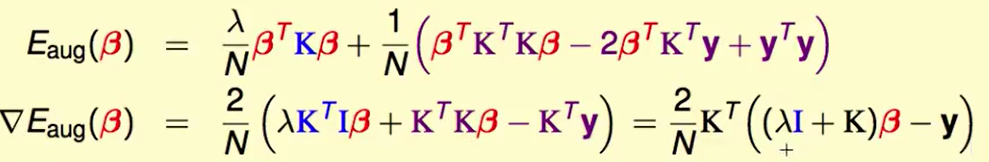
要求最小值，使得梯度=0，那么：

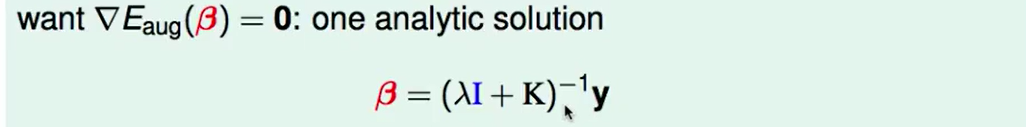
我们来看一下Linear ridge regression和kernel ridge regression的区别：

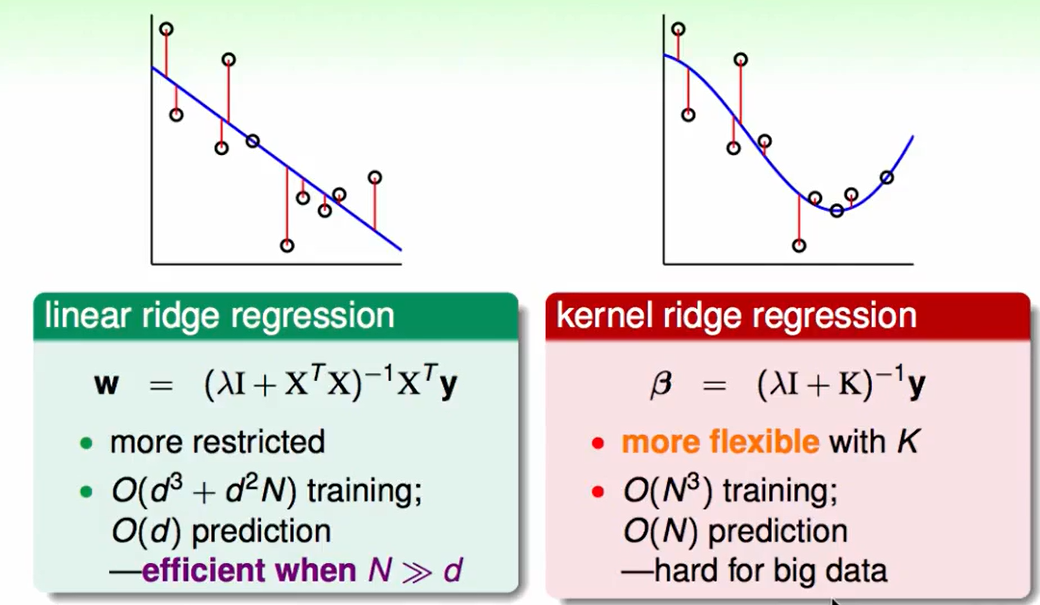
• 在Linear ridge regression种我们训练的时间包含两部分，一个是求$dd$矩阵的逆，所以复杂度是$O(d^3)$, 然后就是$dd$的矩阵与$N*d$的矩阵相乘需要复杂度$O(d^2N)$， 我们预测的复杂度是：$O(d)$,即数据的维度和我们的$w$相乘即可
• 而在Kernel ridge regression种，我们需要对$N*N$的矩阵求逆，那么复杂度是$O(N^3)$, 预策复杂度就是$O(N)$。

不难看出这又是一个trade-off：

Support Vector Regression Primal

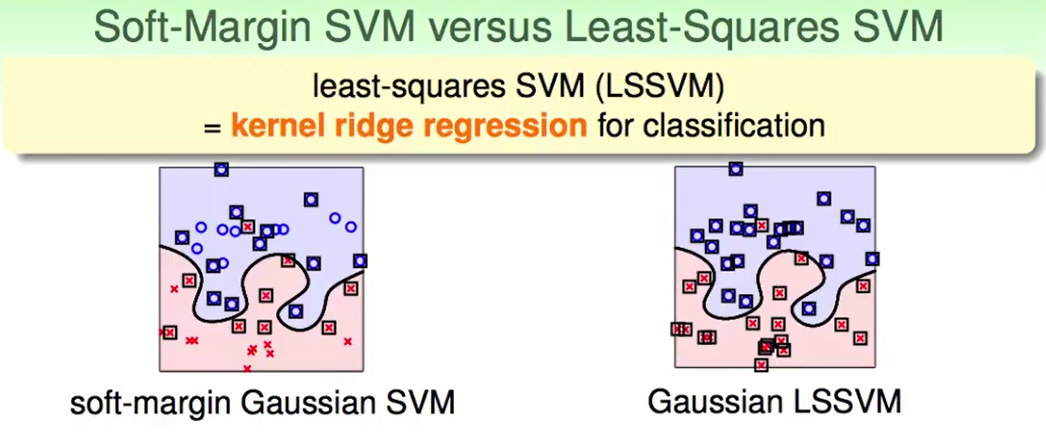
LSSVM 和 soft-margin SVM看起来的得出的结果差不多，但是正方形标出的是support vector，也就是说LSSVM的每个点都是support vector。这就导致了预测很慢。

我们可不可以像标准的soft-margin SVM一样，减少一点Support vector，也就是减少一些$\beta$。

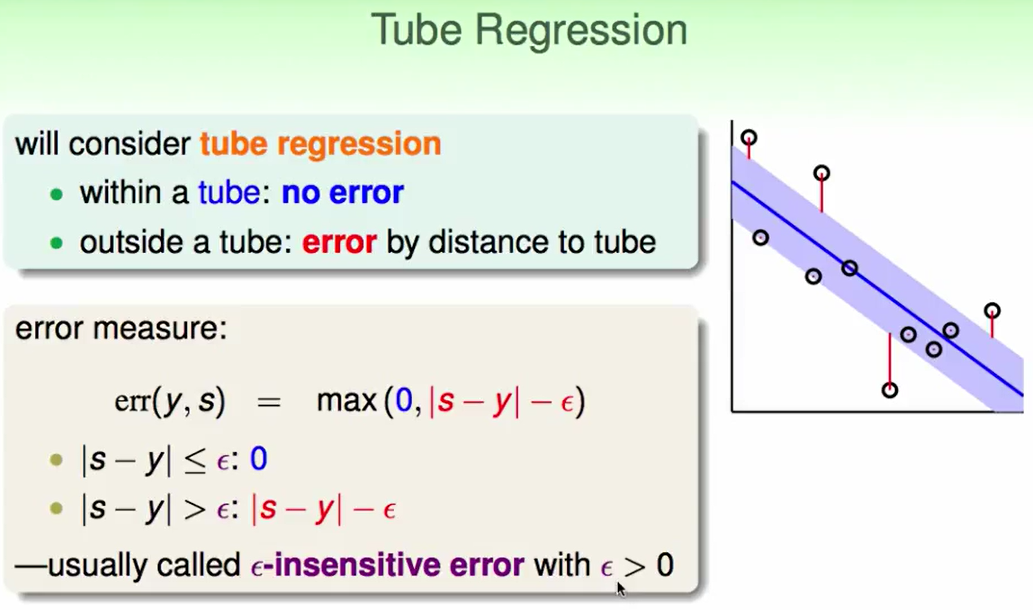
我们还是考虑距离作为错误的衡量方式：

在margin里的说明没有错误，在margin外的错误就是$|s-y|$是到tube中心的长度，$\epsilon$是边界到tube中心的长度，那么错误就是$|s-y|-\epsilon$

我们对比一下这种error measure和squred error measure的区别：

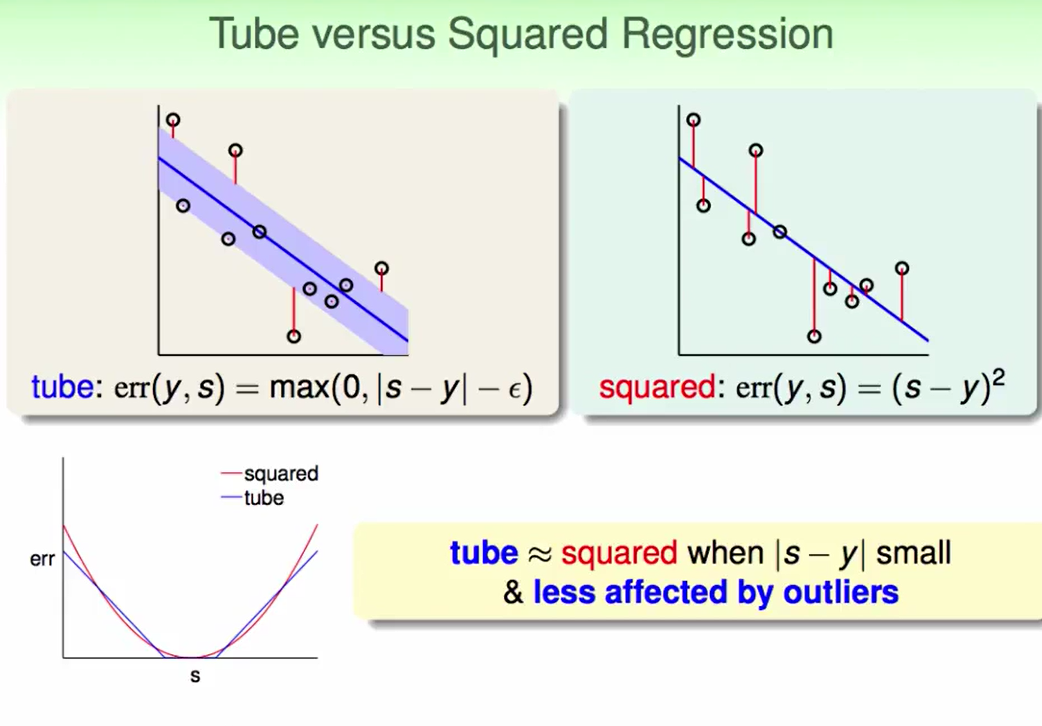
我们发现在$S=y$附近, 两者并无太大的区别，远离$s$我们就会发现tube这种错误率增长速度慢于squred。

因此我们想用standard SVM的方法来解决这个问题：

我们首先考虑转化成standard SVM的形式

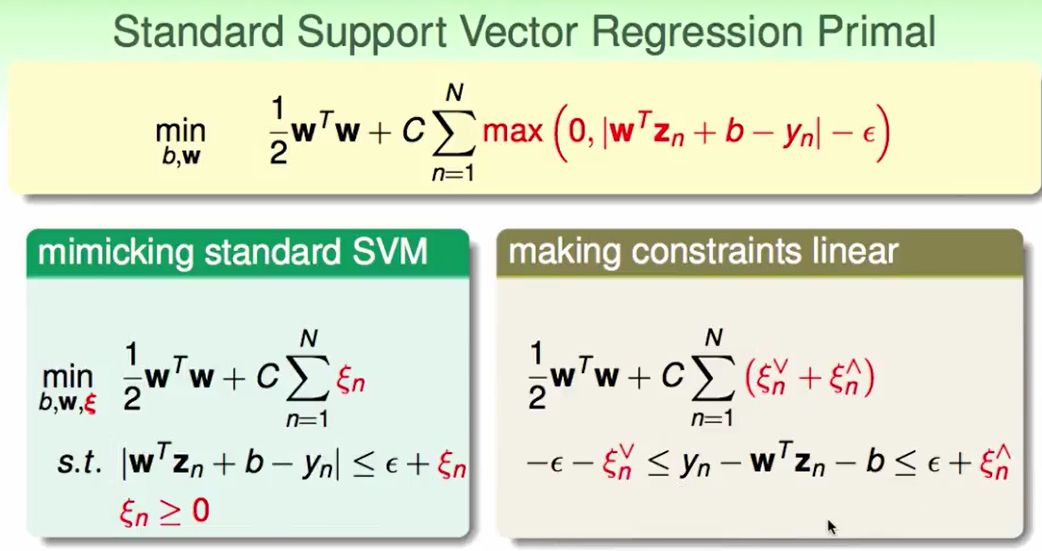
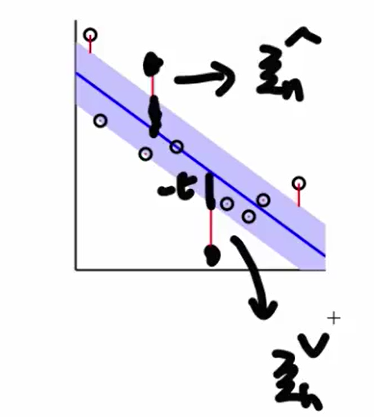
$\xi_n$分为两种，一种是tube上方的，另一种是tube下方的。

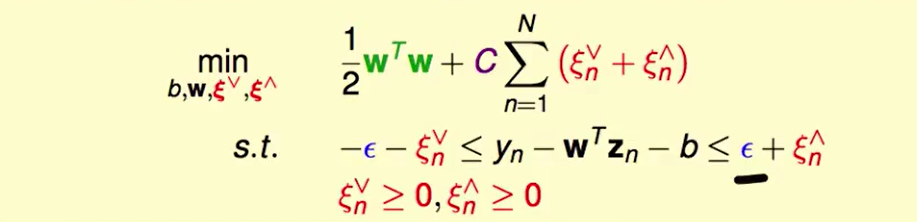
这个$C$代表在乎regularization多一些还是tube violation多一些

与SVM不同的是，除了$C$我们还有一个系数$\epsilon$需要确定。

Support Vector Regression Dual

和Lecture 4一样 写出KKT:

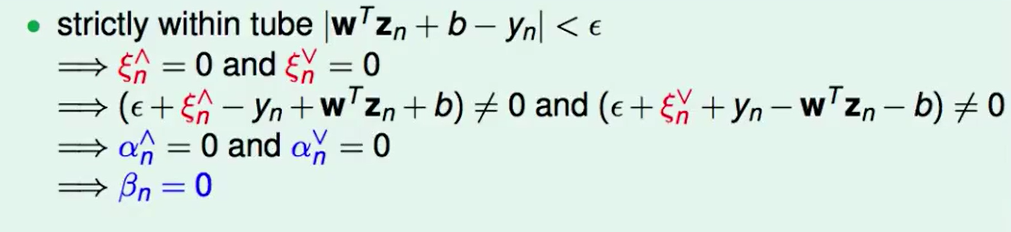
我们来观察tube里的情况推到最后发现$\beta = 0$ ,那么说明这些不会对$w$有贡献,也就是说support vector只包括在tube上或者在tube外的点，因此这样的SVR是稀疏的(sparse)。

Summary of Kernel Model

首先是Linear Models的总结：

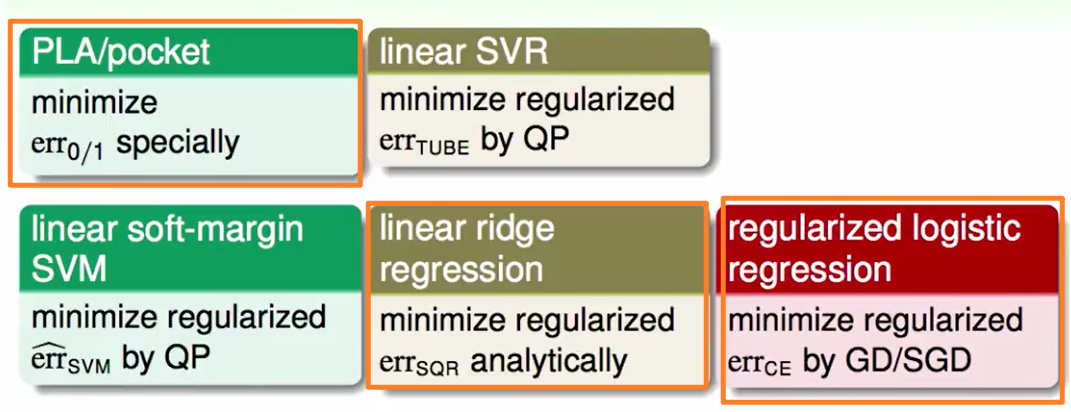
橙色是我们在基石中学到的问题。

后来我们又加上了Linear soft-margin SVM和Linear SVR

绿色/黄色/红色 代表着三种不同的问题。

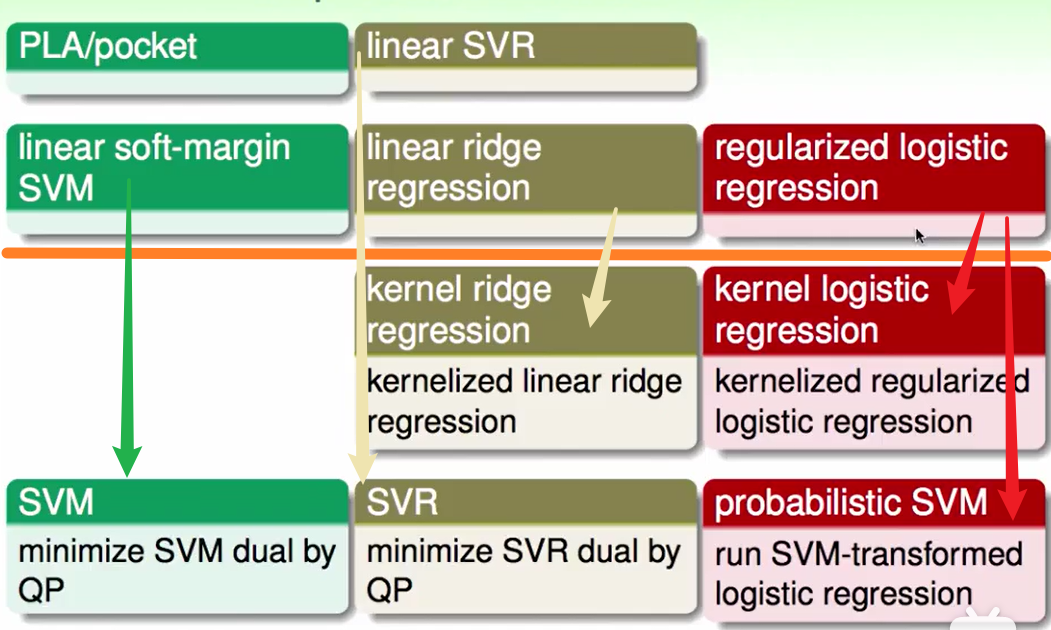
就像feature transform一样，我们有了linear的模型就可以延伸到kernel的模型：

我们总结一下kernel model：