CH15：Matrix Factorization

Linear Network Hypothesis

还记得Netflix推荐系统那个问题吗，他给出的数据$D$ 有两个东西，一个是$\tilde x$，代表着用户的ID,例如：1126，5566，6211

另一个是ID为$n$的人，对电影$m$的评分，我们记为$r_{nm}$。

类似于ID,血型，编程语言 这种feature都是categorical features，也就是类别特征。没有什么具体大小的意义，只是代表某一类。

许多的机器学习模型只能处理数值特征：

但是decision tree可以很好的处理类别特征。

如果我们想要用在数值特征的机器学习模型上，就要对类别特征通过encoding进行feature transform，转换到数值特征。

这里提供一种编码的方式，我们有四个类型，那么就用一个四维的向量来表示每个血型。

再来看看训练资料：

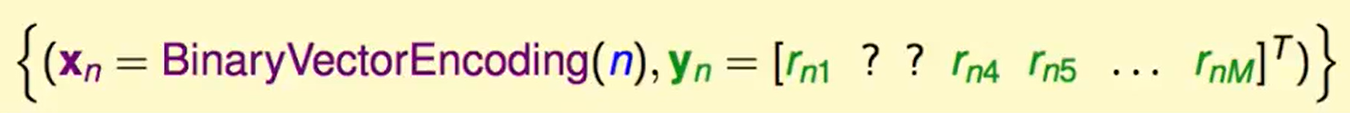
对于每个user他有一串的评分，’?’表示没看过/没评分，我们想从这样的资料里来学到user的喜好。那么下面要做的就是对每个user进行特征精炼，很自然想到的方法就是NNet。

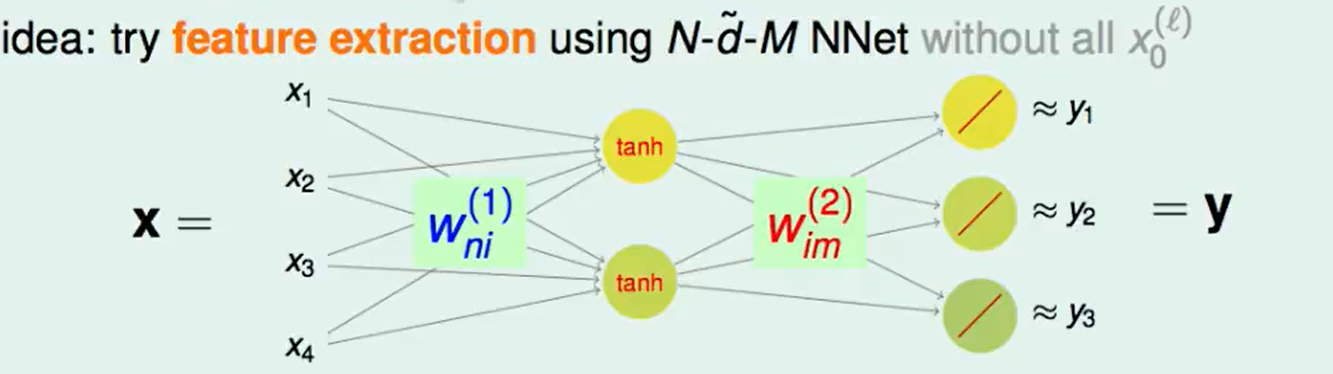
这样的网络的训练输入是：user编码后的id的每一位，输入就是这个user的喜好，这个网络训练完成后，每个$x_i$被赋值为1时，网络就会 输出ID为00…0100…0的喜好(其中的1在第$i$个)。

这样就把复杂的资料存入了这个NNet中。

中间的这个tanh转换是必要的吗？

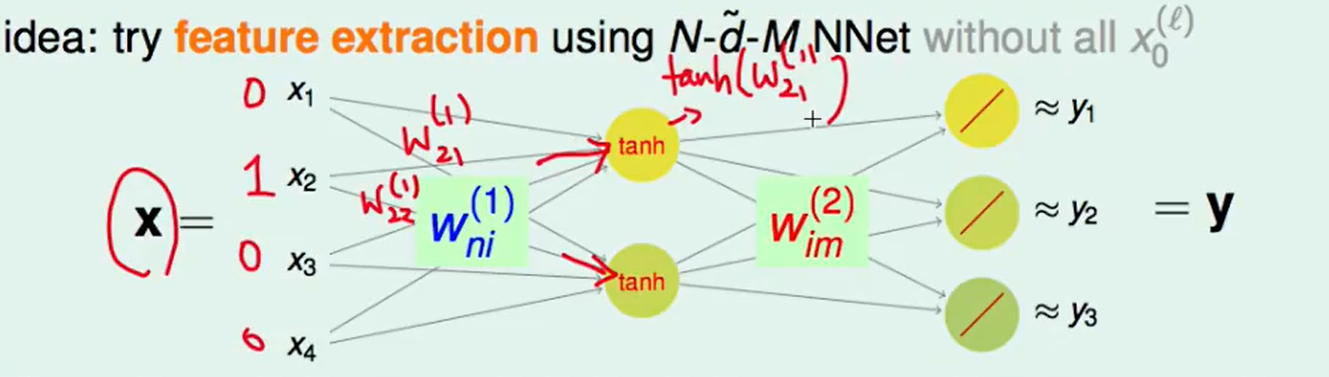
因为我们每次只有一个$x$会等于1，如上图，假设是第二个，经过转换得到就是 $tanh(w{21}^{(1)})$和$tanh(w{22}^{(1)})$，这两个值去组合得到不同的y和$w{21}^{(1)}$,$w{22}^{(1)}$去组合没什么区别，

所以我们可以改成：

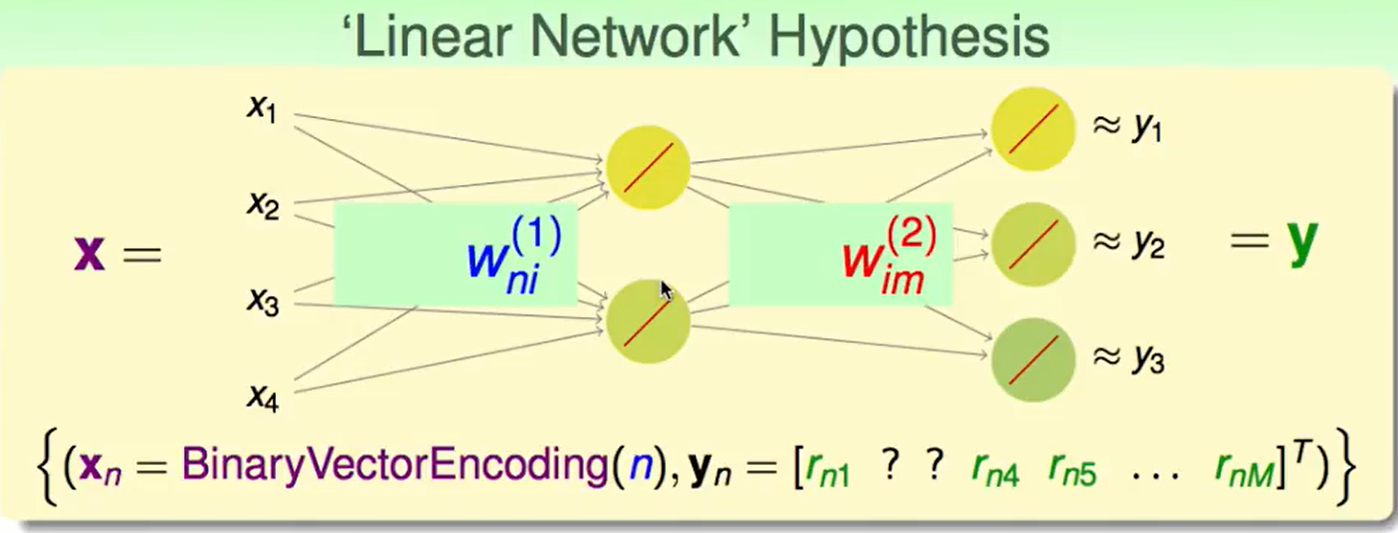
我们对上面的转换矩阵重新命名一下:

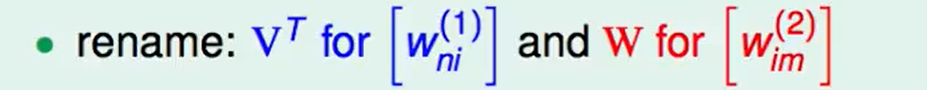
那么我们的网络的函数就可以写成：

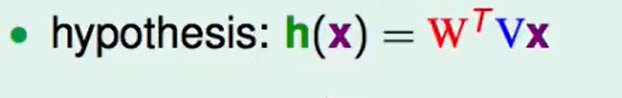
最后得到的结果就是一个$N*1$的矩阵，也就代表了$x$的打分情况。

对一个具体的用户$x_n$来看，式子可以写为：

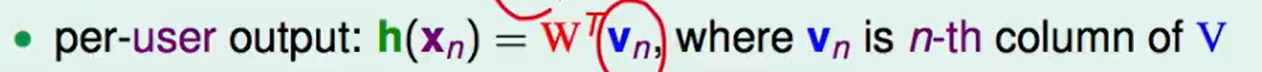
Basic Matrix Factorization

做到这一步，可以把$Vx$看作是对$x$的一种转换，转换为$\phi(x)$,然后再和一个$W^T$相乘。这样就相当于我们把一个user很抽象的特征(ID)转换为了一种对user的具体描述，这个具体描述和$W^T$做一个相乘后就反映了user的电影喜好。

那么我们就可以写出error measure：

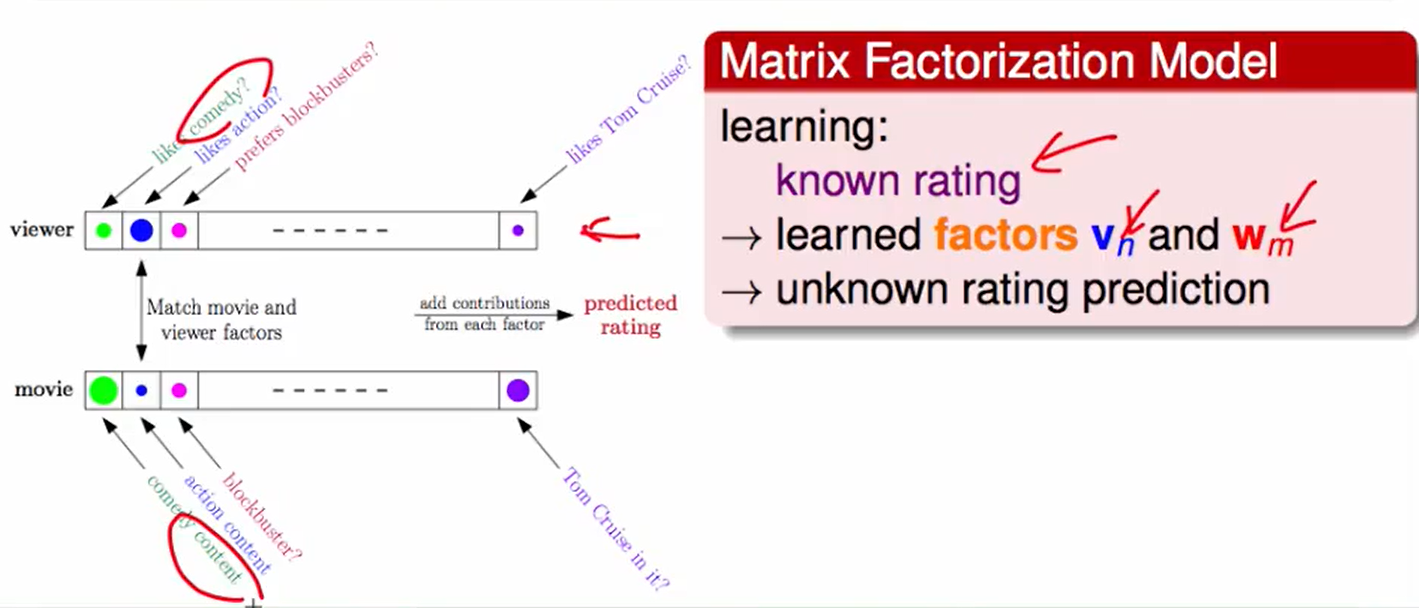
我们的评分总表如下，我们可以拆成两个部分，一个是user自带的特征($v$) 和 电影的特征($w$) 进行计算后就会得到这个人对这个电影的得分。

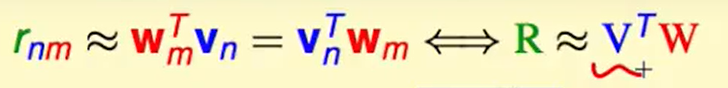
当然这一步是在神经网络上做到的，他提取精炼到的特征信息可能如下，比如$v$ 代表着 [喜不喜欢戏剧，喜不喜欢武打片，……],而movie中提取到的信息就是[包含戏剧内容吗，包含武打内容吗 …….],那么此时我们就学到了这种特征。

下面我们最小化$E_{in}$:

有位有两个变数$V$和$W$,因此我们考虑分别做最优化：

• 当$vn$确定，也就是确定了哪儿个人的时候，我们就最优化每部电影的$w_m$即可，因为我们已知$r{nm}$,$v_n$，而且还是square error，那么我们就可以对每部电影做一个linear regression，这个在insight上的理解就是，确定了某个人，又给了你这个人对每个电影的评分，那么我们就要通过这些数据调整电影的特点，类似于下图，调整一下每个圈的权重，这样就知道电影的风格了。

  

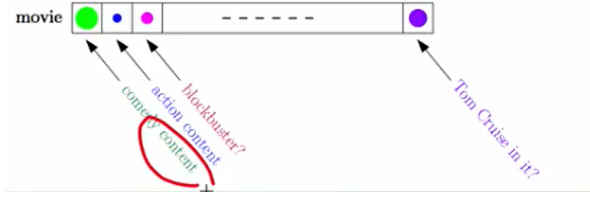
• 当$w_m$确定时，同理，确定了哪儿个电影，有不同的人对他的评分，那么我们就可以对这些人的口味进行训练，得到下图的效果：

这个也可以用linear regression来做。

这种方法叫做：

那么我们提出这种算法Alternating Least Squares(交替最小二乘法)：

Stochastic Gradient Descent

SGD介绍：机器学习基石/CH11：Linear-Models-for-Classification/Stochastic-Grad-Descent（随机梯度下降）

比如现在我们对具体的一个观众来求偏微分，那么$err()$求出来的结果 除了当n=1126都是0。

同理我们就可以写出对第n个观众的偏微分和对第m个电影的偏微分。

那么我也可以用SGD的方式来做：

在基石中最后一节课讲到的的Sampling Bias(抽样偏差)，即我们今年喜欢看的电影和去年喜欢看的电影可能并不是从同一个分布出来的，这有着时间的变化，同时我们今年看的电影更有可能影响我们今年的观影喜好，因此在SGD训练的时候，我们可以选择在SGD最后几百次梯度下降的时候多选择更晚一些的观影评价进行更新。

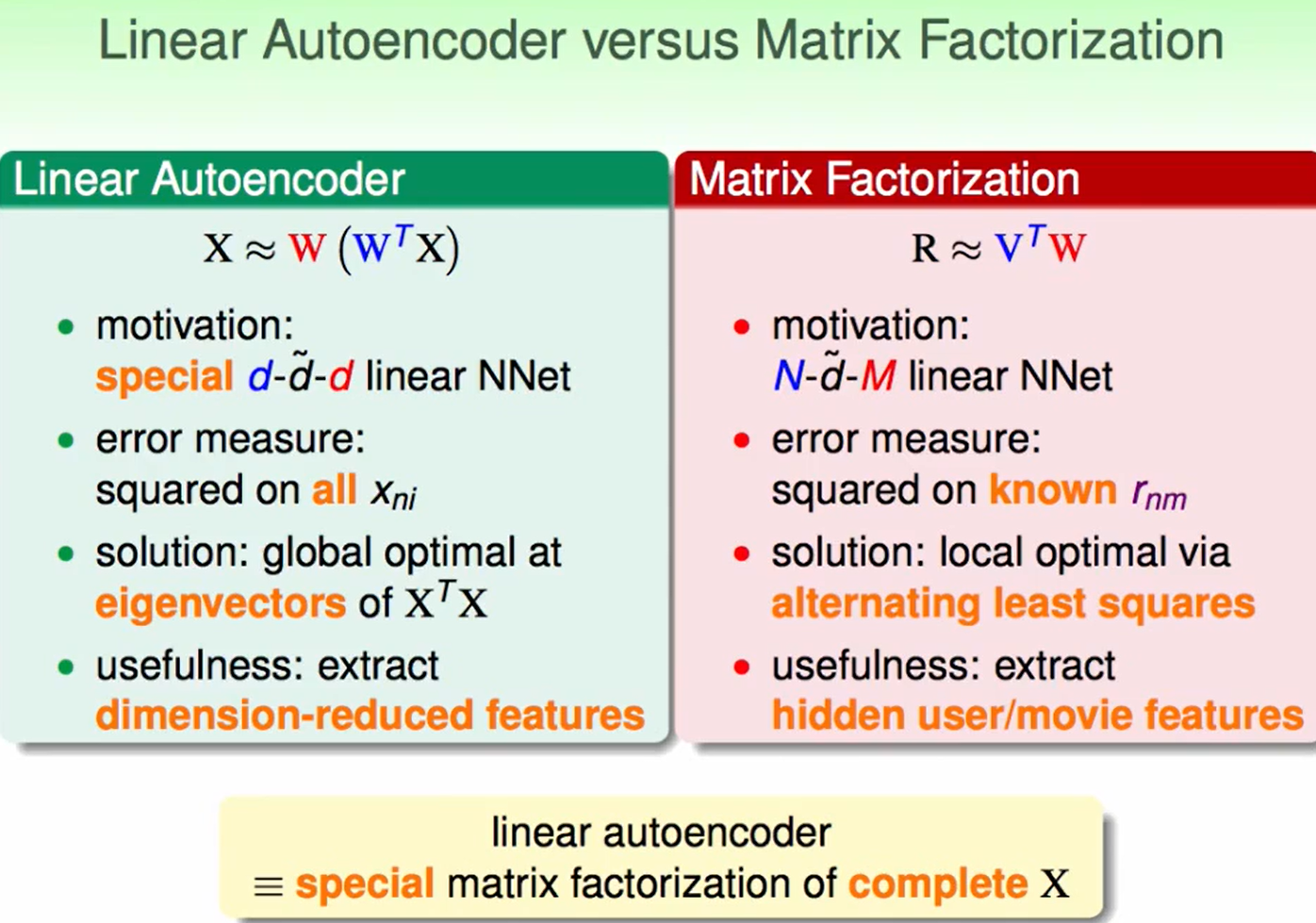
Summary of Extraction Models（提取模型总结）

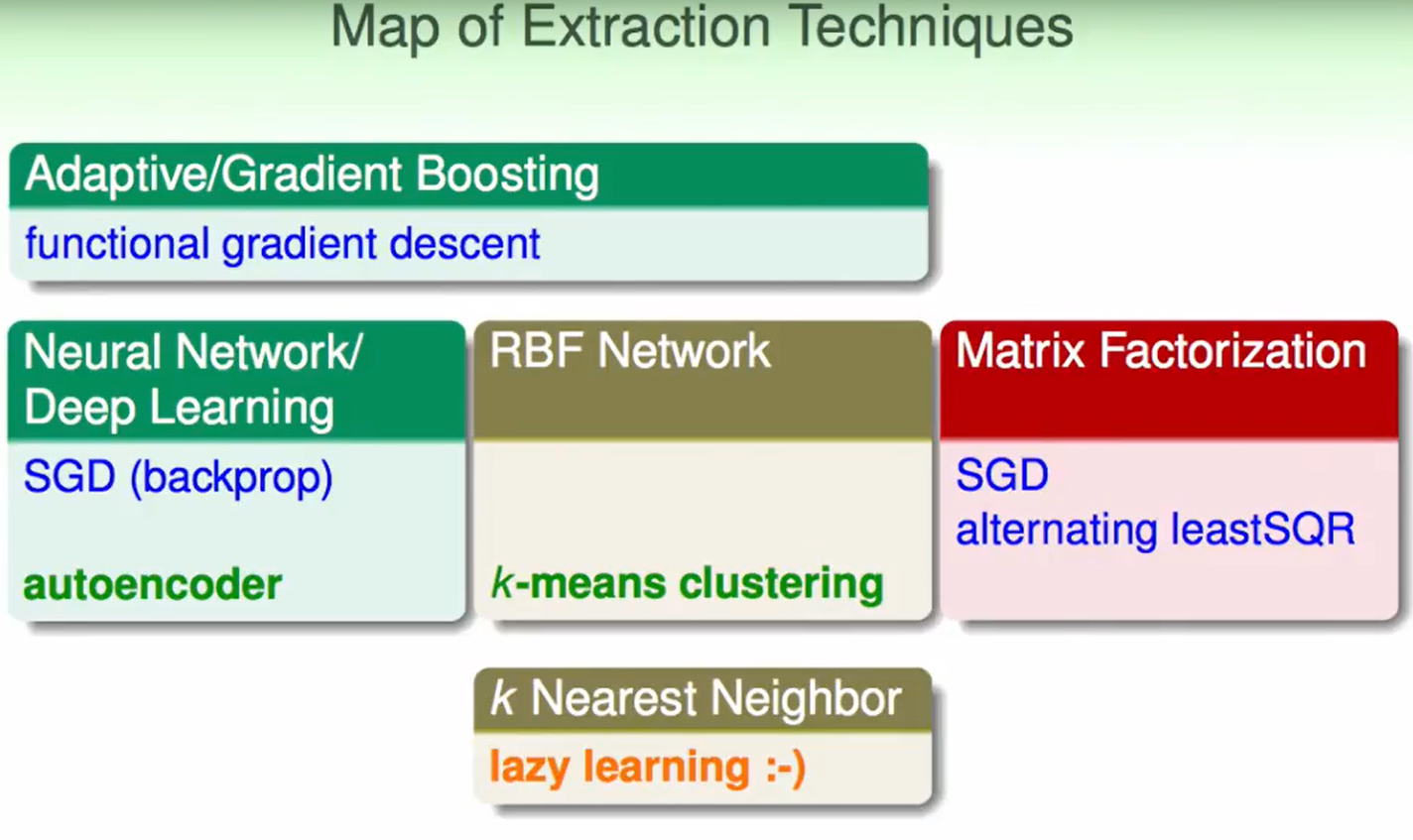
Extraction Models的好处/劣处：