强化学习纲要Ch5-无模型价值函数估计和控制-下
无模型的价值函数估计和控制—下
上一节讲了预测(prediction)问题,这一节我们来解决控制(control)问题。
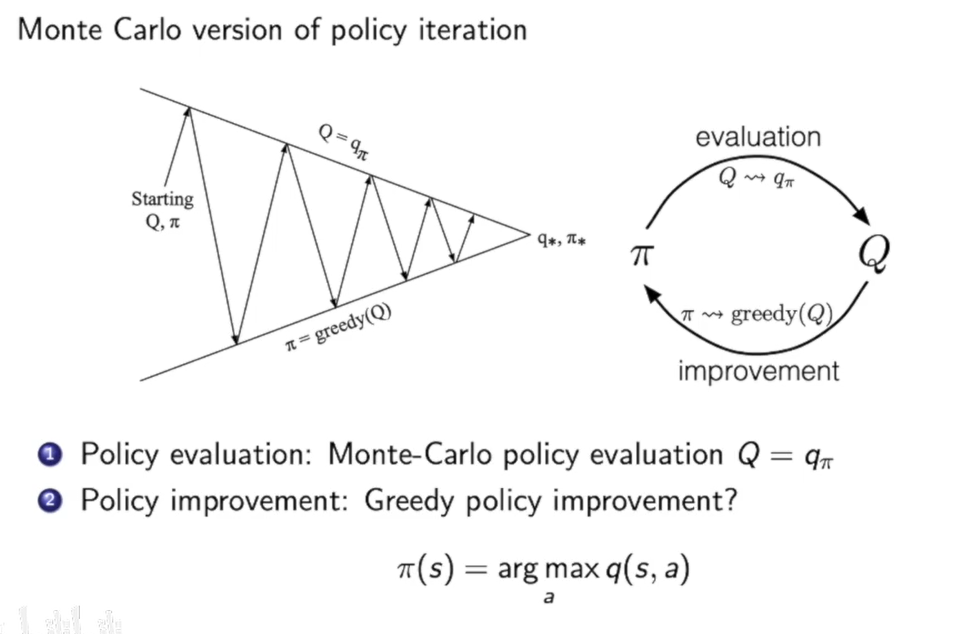
我们之前再policy evaluation中用的方法是动态规划迭代,而上一节提到了一种新的做法也就是通过MC方法来做在特定策略$\pi$下计算状态的价值函数。
model-free时control问题的解决方法:
- 在model-free中,我们首先要用MC方法来填一个表格Q-table,即policy evaluation:
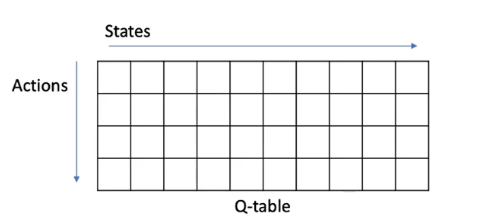
- 然后去更新策略,即control的第二步策略提升policy improvement
在MC算Q-table时有一个trade-off,也就是exploration和exploitation之间的trade-off。

$\epsilon$-Greedy Exploration :
提出了在策略$\pi$下,一个状态在策略$\pi$下不仅可以对应着一个当前收益最大的act,还会有一个随机的act,这个随机的act就是为了exploration。
这个$\epsilon$是可以变化的,在前期可以大一些,后面可以逐渐变小。
MC with $\epsilon$-Greedy Exploration算法有一个特点:在新策略下的价值函数总比以前就策略下的价值函数大。下面给出一个简单的证明:


Sarsa算法(On-Policy TD Control):

Sarsa这名字的来历就是:SARSA分开来看,根据当前状态,做出ACT,得到Reward,然后转移到一个状态,做出新的ACT。
伪代码:

即然存在n-step TD,那么也会存在n-step sarsa。
On-policy vs. Off-policy Learning:
On-policy是 学习策略$\pi$通过策略$\pi$所产生的轨迹数据。
Off-policy是指在学习策略$\pi$时,用了两种策略产生轨迹数据给他学习:一种策略是现在学到的策略,也是我们希望最优化的策略,我们一般称之为目标策略target policy $\pi$。另一个 策略是我们拿来探索的策略,那么这个探索的策略可以激进一些,我们称之为行为策略behavior policy $\mu$ ,这个行为策略通过探索找到一些新的轨迹数据,然后再喂给target policy来学习。
on-policy 与 off-policy的本质区别在于:更新Q值时所使用的方法是沿用既定的策略(on-policy)还是使用 新策略(off-policy)。
Off-Policy Control with Q-Learning:

Q-Learning 就是一种Off-Policy的算法,一种target policy是按照贪心的方法选择当前已知最好的方法去更新,另一种就是behavior policy,但是这里她并没有采用完全的随机,因为完全的随机其实一般效果不会那么好,我们可以用$\epsilon-greedy$的方法,前期$\epsilon$可以大一些随机性强一些,以后$\epsilon$调到低一些即可。

Q-Learning vs. Sarsa:

从backup这个图上来看:
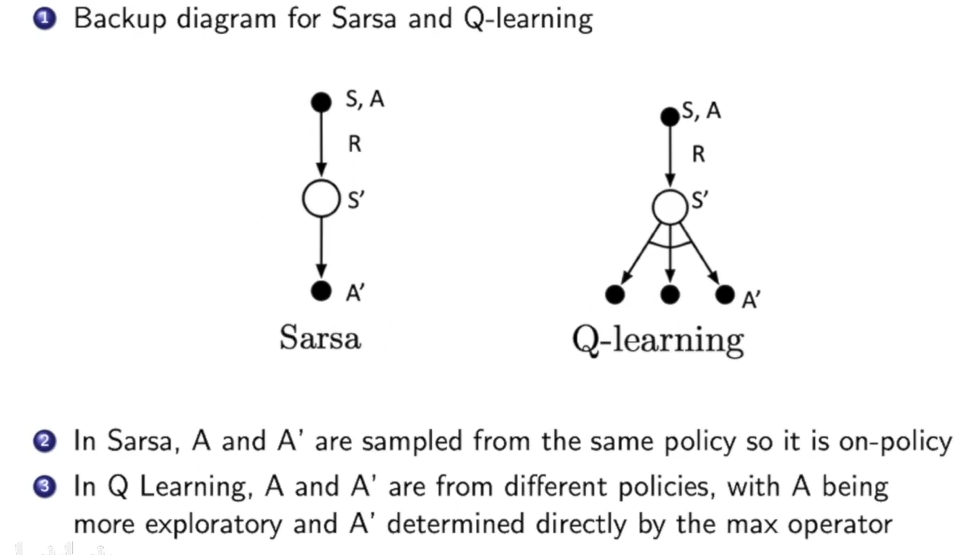
Sarsa中的A’ 是通过和A一样,从策略当前的策略抽取到的。而Q-Learning中,他是通过观察Q-Table,找到一个可以使得$Q(S_{t+1},a)$最大的$a$。
cliff walk问题中,看一下Sarsa和Q-learning的区别:
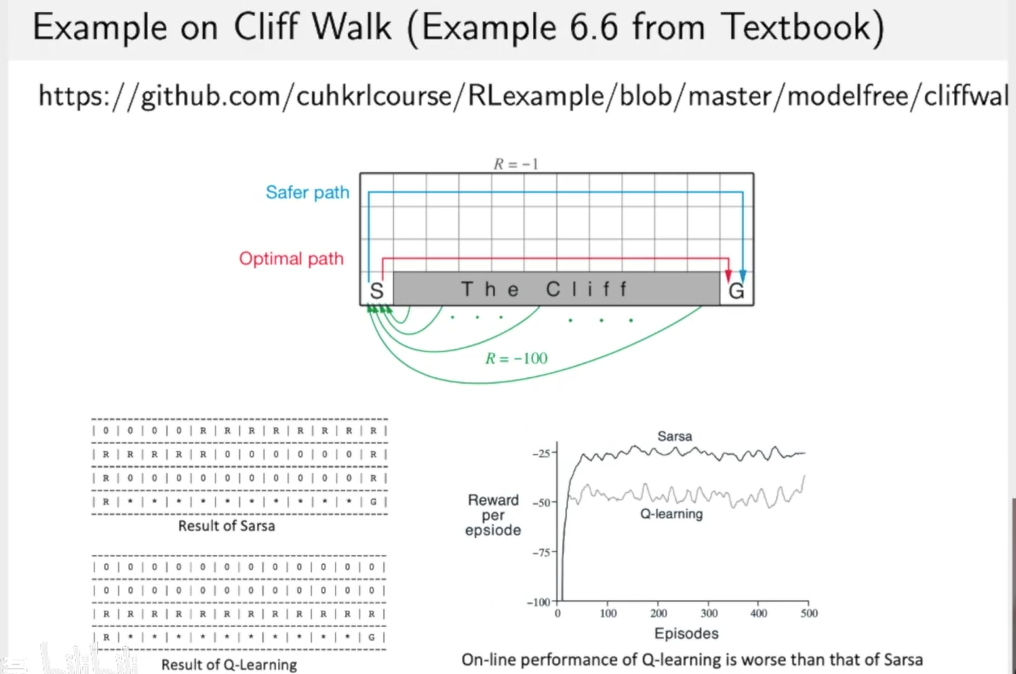
Q-learning的策略更激进,Sarsa的策略更稳健。
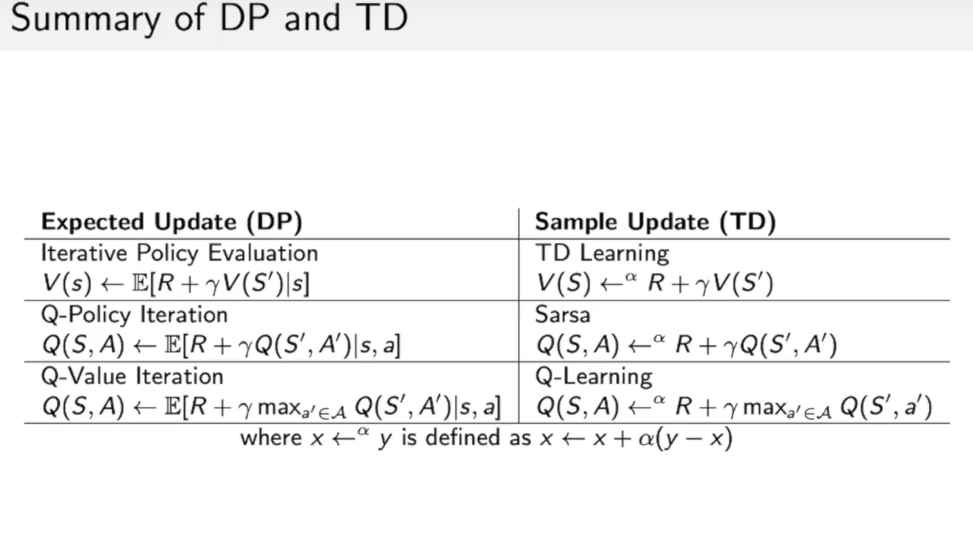
总计:
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!