价值函数近似—上

Plan：

前面提到的状态量都很小，而许多实际环境得状态量是很多的：

比如围棋局面高达：$10^{170}$, 那么这么多的状态必然是不能有概率转移矩阵的，因此状态很多的强化学习任务一般也都是model-free的。

回想之前在model-free中我们是怎么进行policy evaluation的？ 是通过填写Q-Table。

而在状态数过多时，填写Q-table根本不可能。

这里一个trival的想法就是函数近似：

我们想通过见过的状态来近似估计出价值函数，状态动作函数，策略函数等，希望可以泛化到未见过的状态上。

比如对于价值函数$v$, 可以这样设计：

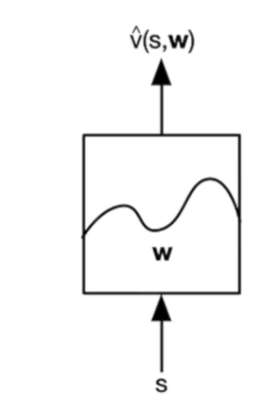
输入状态，通过学习$w$,最后得到价值函数$v(s,w)$

对于状态动作函数$q$, 有两种可行的设计方式:

一种是输入状态s和动作a，学习参数w，得到q(s,a,w):

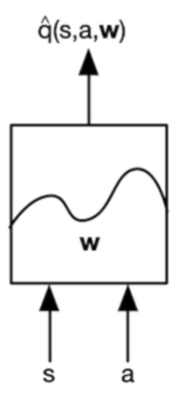
另一种方法是，通过输入状态，学习参数w，得到各种动作的q值，然后我们使用时直接加一个argmax即可：

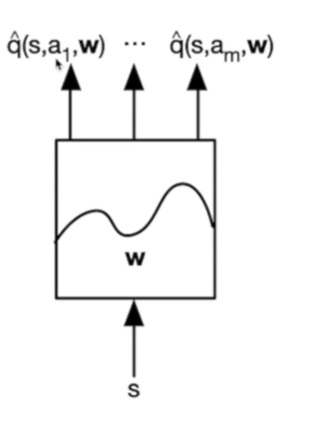
对于函数估计：

• 可以采用线性的把feature combine起来
• 神经网络
• 决策树
• 近邻(Nearest Neighbour)算法

我们这里假设我们已经指导真正的价值函数$v^{\pi}$，我们的近似函数为$\hat{v}$ ：

通过上图计算它们的差距$J(w)$,最小化$J(w)$ 就是我们现在的任务，可以使用梯度下降来做。

状态的表示方法：

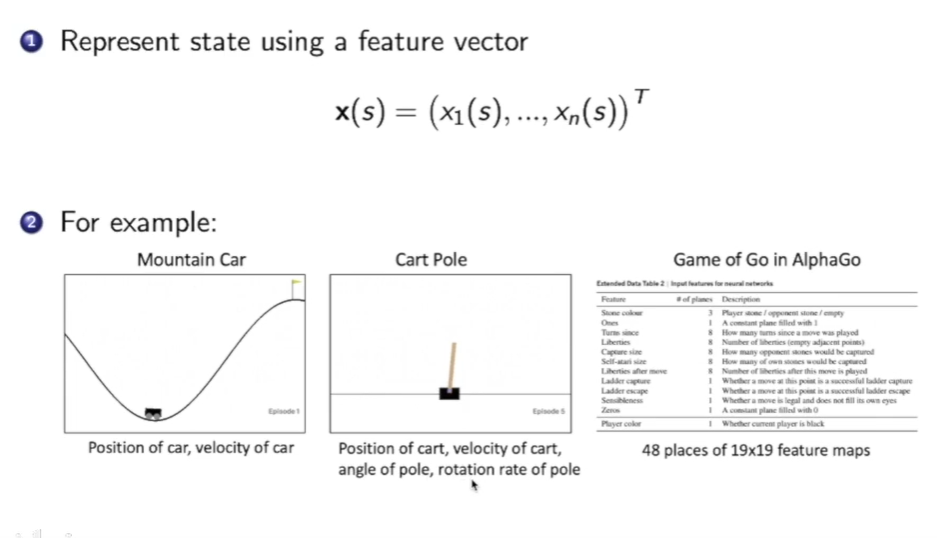
状态可以用一个向量$x(s) = (x_1(s),…,x_n(s))^T$来表示，向量中可以有很多东西：比如在上图左下角的mountain car中，我们可以选择车的位置，车的速度。在 cart pole游戏中可以选择木块的位置，木块的速度，杆的角度，杆上端的速度等…

线性模型来拟合函数：

可以写为：

$$\hat{v}(s, \mathbf{w})=\mathbf{x}(s)^{T} \mathbf{w}=\sum_{j=1}^{n} x_{j}(s) w_{j}$$

所以现在目标函数可以写为：

$$J(\mathbf{w})=\mathbb{E}_{\pi}\left[\left(v^{\pi}(s)-\mathbf{x}(s)^{T} \mathbf{w}\right)^{2}\right]$$

那么他的梯度+stepsize设置为$\alpha$时可以表示为：

$$\Delta \mathbf{w}=\alpha\left(v^{\pi}(s)-\hat{v}(s, \mathbf{w})\right) \mathbf{x}(s)$$

然后梯度下降。

这里运用了一个Table lookup feature的写法：

他把多个$x(s)$组合在一起变成一个表$x^{table}(s)=(1(s=s_1),…,1(s=s_n))$ ,这样的方法类似于one-hot编码，是哪儿个状态就对应位置是1向量 ，其他是0向量。

因此:$\hat{v}(s, \mathbf{w})=\left(\mathbf{1}\left(s=s{1}\right), \ldots, \mathbf{1}\left(s=s{n}\right)\right)\left(w{1}, \ldots, w{n}\right)^{T}$，其中$w_i$在此时代表权重向量$w$和$x(s_i)$的向量乘积。

预测(Prediction)问题, 怎么求价值函数：

之前都是再假设我们有$v^\pi$,但实际上我们并没有，因此可以借用model-free中的想法，用MC或者TD的方法来估计并代替$v^\pi$：

原式为：

现在我们要用MC的方法或者TD的方法来搞：

下面我们详细的说一下MC和TD的方法

• MC方法：

MC的方法是无偏的估计，但是由于抽取单个一般都是噪音很大的，因此我们需要选取多个求平均。

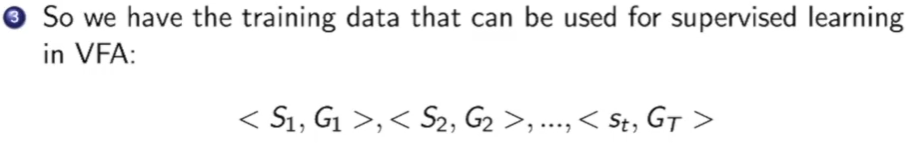
这样我们就可以产生一些trainning 数据，它是一个个Pair。

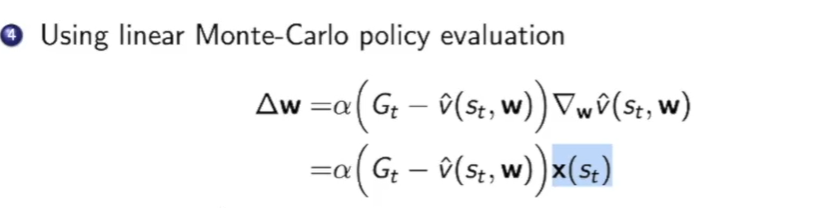
在线性模型中$\Delta_W\hat{v}(s_t,w)$是一个线性的，即xw，因此可以直接求偏导得出$x(s_t)$

• TD方法：

TD方法用TD target代替了真实价值。这是一个有偏的，因为TD target的抽样期望并不等于$v^\pi(s_t)$, 因为TD target中包含了我们上次的估计，这种在估计上估计肯定是有偏的。

因此我们也可以把这种方法发到control问题的第一步policy evalution

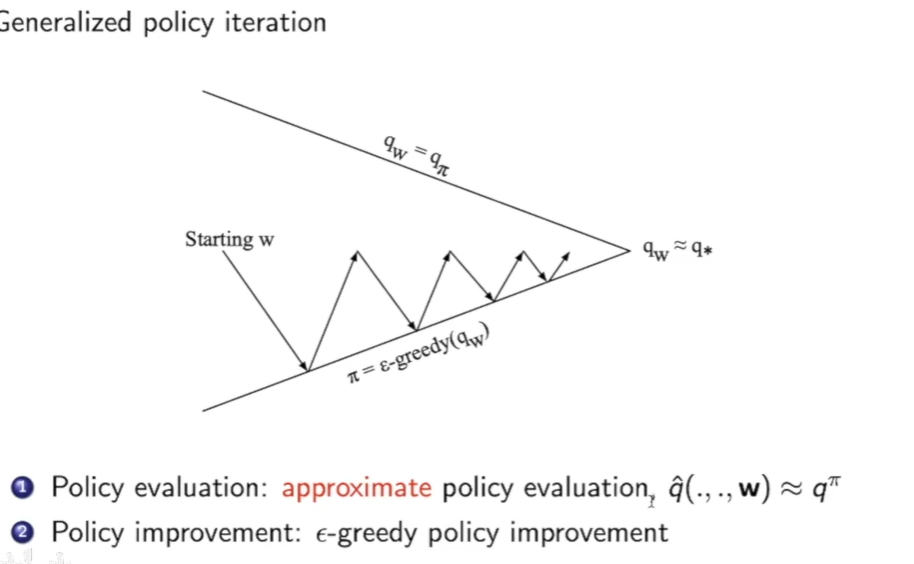
拟合行为价值函数，和状态价值函数相同的方法：

这里我们还是假设行为价值函数Action-Value Function是一个通过不同feature线性的组合得到的函数：

由于我们还是和之前一样假设了我们已知q函数，但实际上我们是不知道的，因此还是需要TD Target或者MC的抽样来做替换。

总结：

上面算法进行更新时有关收敛的问题：

• TD Target对w的梯度包含了w，这其实是不太准确的。
• 首先TD Target和就是一个估计的过程，我们用这个估计出来的值去做梯度下降，去估计价值函数，这有太大的不确定性。
• 上面我们都是在用linear的function，事实上，当我们使用non-linear function进行拟合时或者是off-policy的方法进行拟合时结果非常不稳定。

强化学习训练不稳定的原因：

• 函数估计所造成的误差
• Bootstrapping会使得估计是在之前估计的基础上估计的，比如TD Target的第二项本来就是估计的，现在却要用这个估计的来更新训练估计价值函数。
• off-policy训练中，采集到的数据是behavior policy所得到的，而我们优化的函数确实在另一个数据分布上的函数。

有关能否找到最优解的问题：

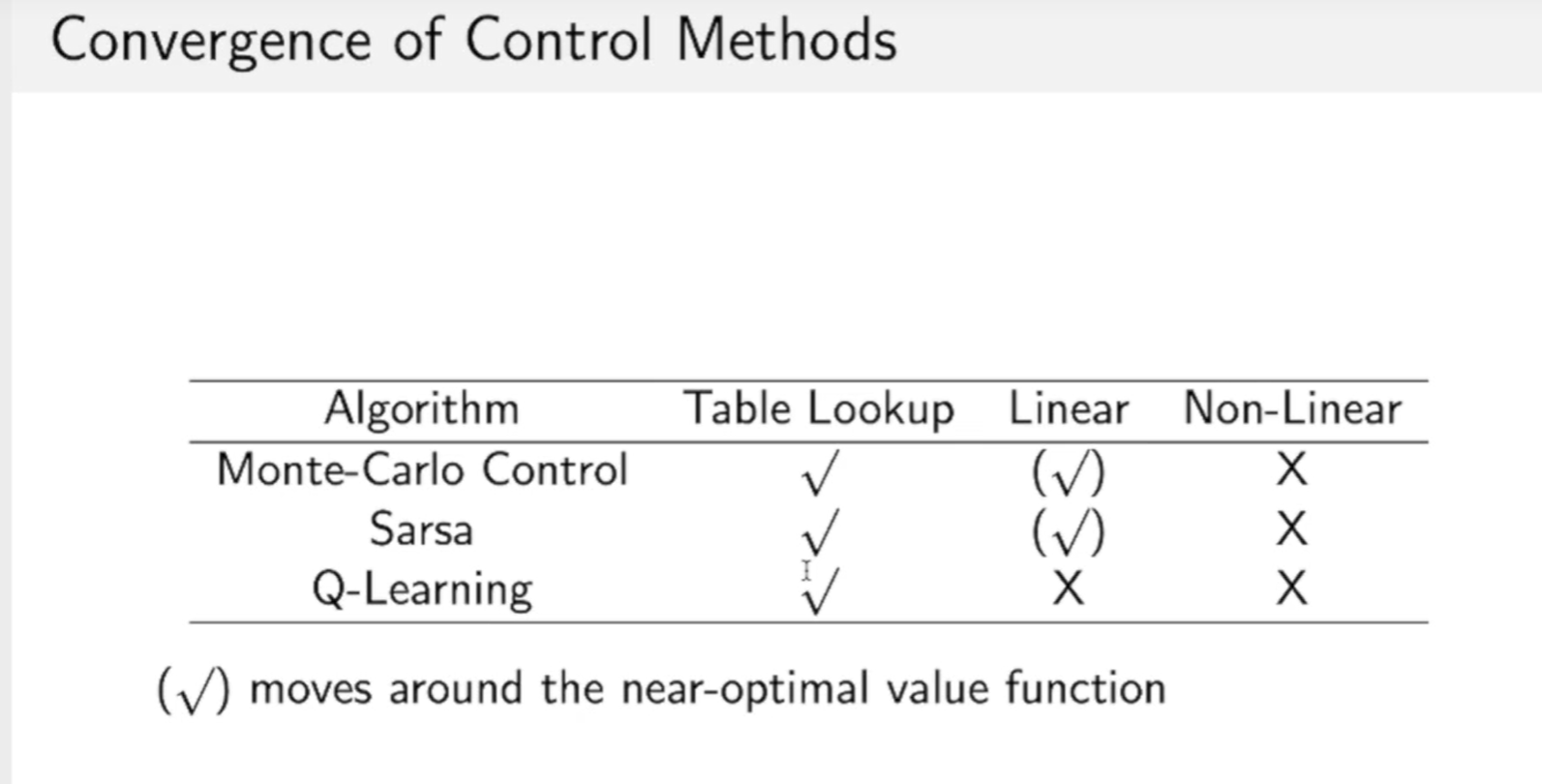
• 用Table Lookup方法一般都是可以找到最优解的。

• 在Linear的算法中，MC，Sarsa可以找到一个近似最优解的算法。而Q-Learning还是比较难找一个最优解。

• Non-Linear算法下，三种方法都无法保证最优解。

现在我们优化的方法都是单步的优化，我们可以每次优化一个batch：

假设我们有一堆数据$D$, 数据类型为<状态，实际价值>，这里的实际价值可以用TD Target或者MC中的$G_t$来替换。

我们的目标是最优化w，使得w可以最好的fit model，也就是最小化$E_D$。

因此我们可以用mini-batch 的SGD来做梯度下降。