强化学习纲要Ch8-策略优化基础-上
策略优化基础——上
Value-based RL vs. Policy-based RL
Value-based RL vs. Policy-based RL:
- Value-based RL
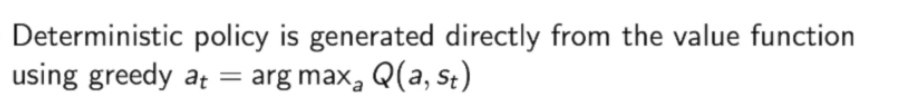
Value-based Policy是默认策略是determinsitic的,也就是说我们的策略选择并且只选择能使得$Q(a,s_t)$价值函数最大的那个action.
- Policy-based RL

基于策略的强化学习不同于基于价值的强化学习,他的策略选择是通过$\pi_\theta(a|s)$这个动作概率分布来采样决定当前的动作是什么,其中$\theta$是一个要通过数据学习的参数。

Policy-based RL 的好处:
不管数据有多么的少,我们还是可以训练出一个策略函数,虽然可能并不是很好,当数据变多,效果就会变好。而在Value-Based RL中价值函数的估计是需要整个的table,这个对数据的要求远大于Policy-based RL 。
Policy gradient在高维空间中更有效。
- Policy gradient学到的是一个概率分布。
缺点:
- 可能会收敛到局部最优解
- 计算一个策略时,他的方差很大,每次训练得出的效果差别较大。
下面先来介绍一下策略:
策略有两种类型,一种是Deterministic的,另一种为stochastic的。
- deterministic:给定一个状态,策略返回一个确定的action。
- stochastic: 给定一个状态,策略返回一个动作的概率分布(比如40%往左走,60%向右走)。
比如在石头剪刀布中: 一个确定性的策略很多容易被打败,而用概率分布比如每个动作各33%的概率出手,就会好很多。
再举一个例子说明stochastic policy的好处,如下图:
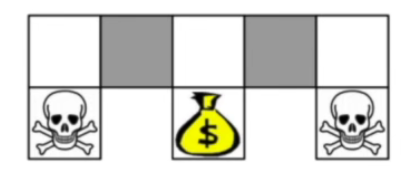
比如这样的一个游戏,深色方块是一个魔幻的地方,进去的玩家不知道这是左边的深色格子还是右边的深色格子,换句话说在这两个格子时环境的状态一摸一样,因此在deterministic policy下我们会得到一摸一样且唯一的action。 那么我们经过学习后就会发现,在白色区域时,下面的格子是骷髅头,那么就会往边上走,而在金币处会向下走,在深色格子处无论向哪儿边走都会导致一边被困住,如下图。
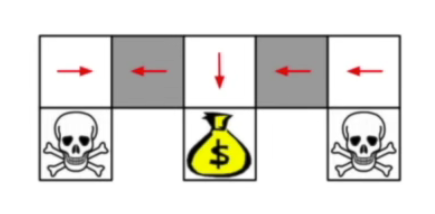
而如果利用stochastic policy:
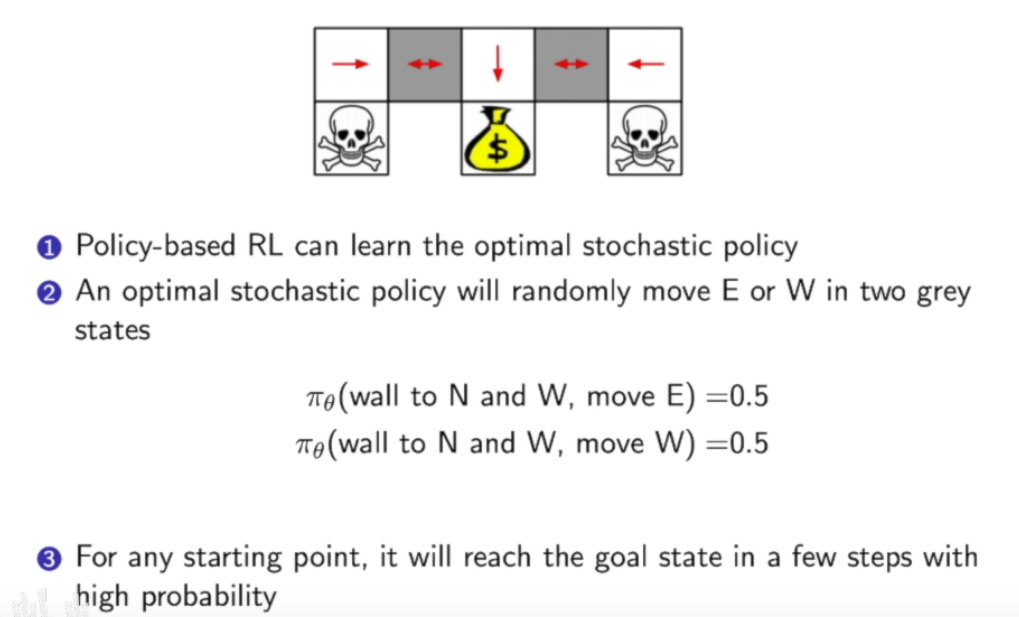
策略函数的优化

我们优化的目标是优化策略参数$\theta$
首先的问题是怎么衡量$\pi_\theta$的好坏呢?
- 如果在一个有终止的环境(episodic environment)中,我们可以用开始状态$s_1$的价值的期望来表示:
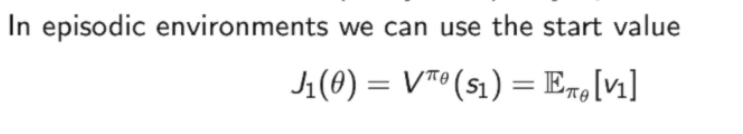
- 如果是在一个连续无终止的环境下(continuing environment),我们可以用状态的平均价值:

也可以用每一步的平均回报:

策略的价值也可以从轨迹中来看:
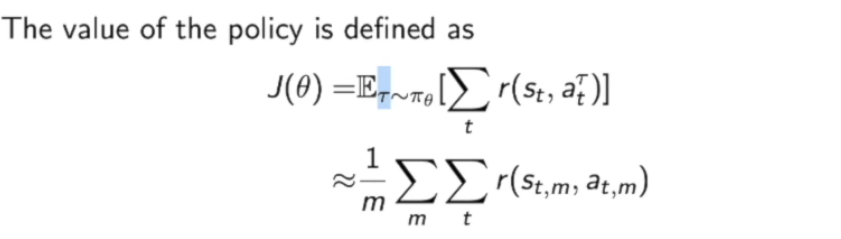
我们这里假设$\gamma$ 是一个轨迹,这个轨迹从策略$\pi_\theta$中来进行采样,然后去计算采样的轨迹所得到奖励的期望。数学表达就是采样$m$条轨迹,计算这些轨迹的平均奖励。
而我们的优化目标就是:
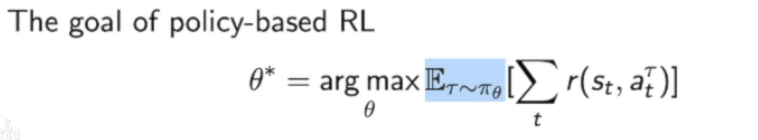
Policy-based RL的优化目标是:

优化方法为:
- 如果$J(\theta)$是可导的:

可以用梯度上升(梯度下降反着走),共轭梯度法,或者拟牛顿法。
如果$J(\theta)$不可导:可以用黑盒优化相关的算法

比如 交叉熵方法,爬山算法 (Hill climbing),进化算法。

迭代N次,对于每次迭代:
首先假设我们参数的分布函数$P_{\mu^{(i)}}(\theta)$,这个分布函数初始化可以是一个高斯分布,然后从这个参数的分布函数进行抽样,抽取出m组参数。
然后对这m组参数,分别计算在每组参数$\theta$下的$J(\theta)$ 并存于$C$这个集合中。
接着,我们在$C$中挑选出集合$J(\theta)$前10%大的的$\theta$, 然后再用这些$\theta$来优化分布函数中的参数,从而使得参数分布进行了更新。
还有一种方法是用差值来代替梯度:
他算出每个维度的梯度

计算策略梯度:

第三部中用了一个小技巧:把 $\nabla\pi\theta/\pi\theta$换为了score function$\nabla ln\pi$。
策略函数的形式
第一种是Softmax Policy:

在某个状态$s$下,首先把$\phi(s,a)^T$这个对原特征做完feature transform后再做一个线性组合得到:$\phi(s,a)^T\theta$。
最后转换成概率,得到$\pi_\theta$:

另一种策略函数的形式是Gaussian Policy:
有些时候策略是连续的,比如机器人控制问题,动作空间是个连续的过程,需要连续控制变量。对于连续策略变量,高斯是一个比较好的定义方式。
首先把状态特征量的线性组合作为高斯函数的均值,方差Variance既可以把它参数化也可以把它设为固定的$\sigma^2$。

所以当我们要得到一个动作时,就直接对高斯函数进行采样,这样我们就可以得到连续的值::

这里的score function是:

Monte-Carlo policy gradient
Policy Gradient是策略优化的一个经典算法,先说MDP最简单的形式——只走一步
Policy Gradient for one-step MDPs:
这个方法只走一步,用一步的reward来进行计算:
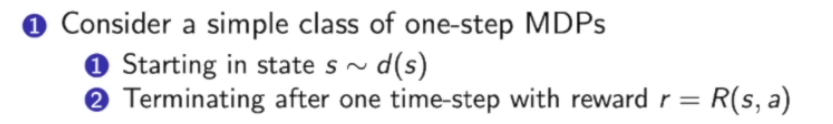
然后写出$J(\theta)$的表示函数:

计算梯度,这里计算梯度用到了上面提到的score function的技巧:
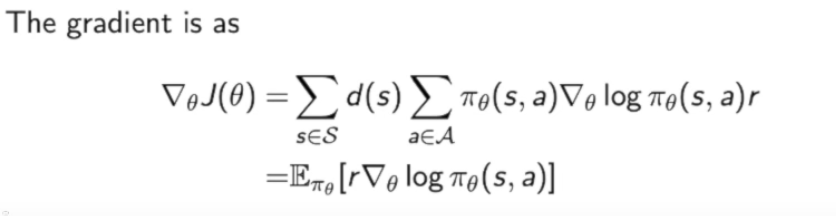
Policy Gradient for Multi-step MDPs

首先从策略中抽样出很多轨迹
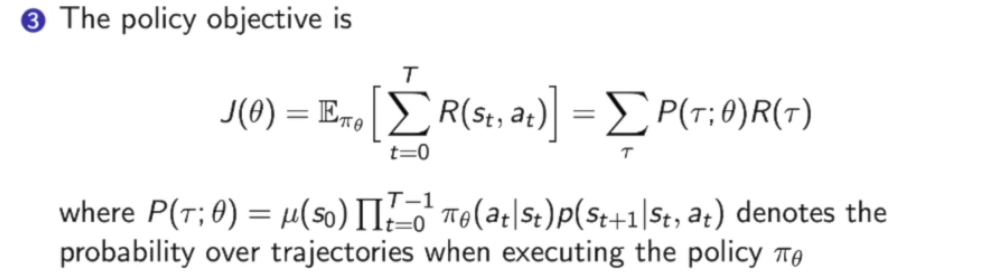
然后计算轨迹的期望作为$J(\theta)$。
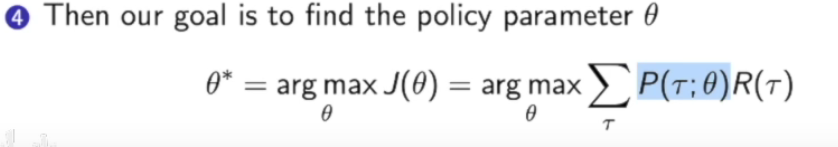
此时我们的需要优化的参数$\theta$已经被包含到了关于轨迹的概率函数,现在我们的目标就是优化这个$\theta$使得$J(\theta)$最大。
Multi-step MDPs的策略梯度是什么?

那么现在就得到了策略梯度:
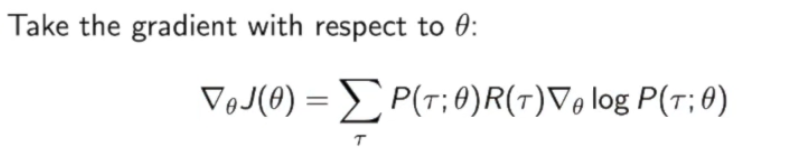
因为我们实际上并不知道这个轨迹$\tau$的分布,所以我们一般会用蒙特卡罗的方法来代替:
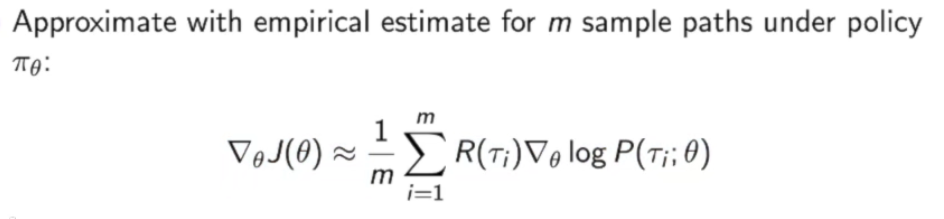
下面要对$logP(\tau_i;\theta)$分解:
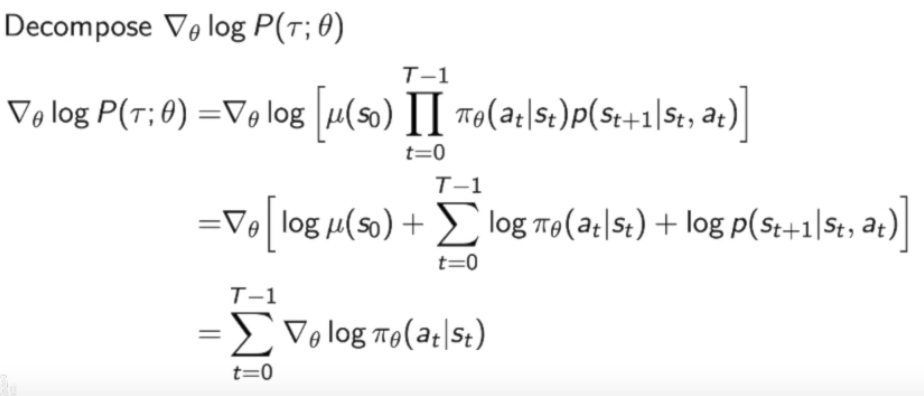
这里也体现了我们写成log这种技巧的好处到底是什么,他将一些没用的量扔了出去,并变成了score funciton的加和。
那么现在我们可以把

本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!