GAMES101(5-6):Rasterization和反走样

GAMES101(5-6):Rasterization和反走样

Rasterization(Triangles)

简单来说光栅化的目的就是将想要展现的物体给真正现实到屏幕上的过程，因为我们的物体其实都是一个个顶点数据来表示的，如何表这些蕴含几何信息的数据转化为屏幕上的像素就是光栅化所考虑的东西。比如说一条直线，究竟该用哪些像素点去逼近它，一个三角形，又用哪些像素集合表示它，这都是光栅化的过程。

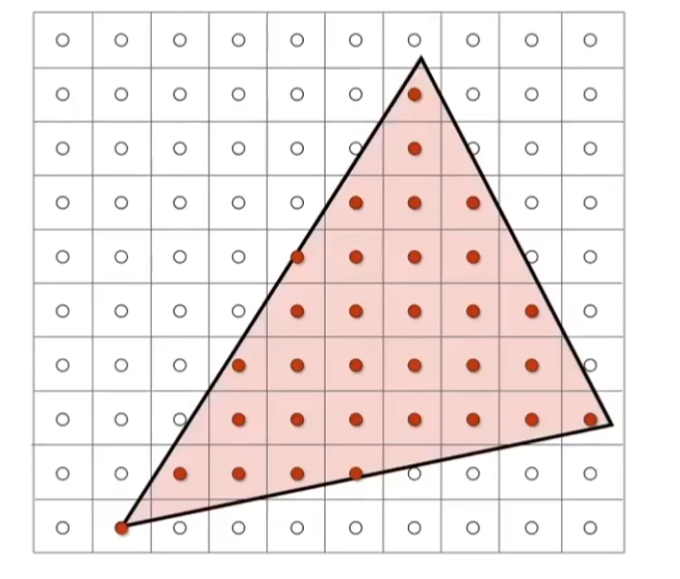
image-20220627201503729

采样的方法：也就是判断每个点是不是再三角形内。

image-20220627201537420

怎么计算是否在三角形内？叉积，看是不是在同一侧。我们也需要注意下在三角形边上的处理，即叉积等于0的情况，可以认为在三角形内/也可以认为在三角形外。

如何加速这个过程，对于一些一定不可能的点无需判断是否在三角形内：包围盒！

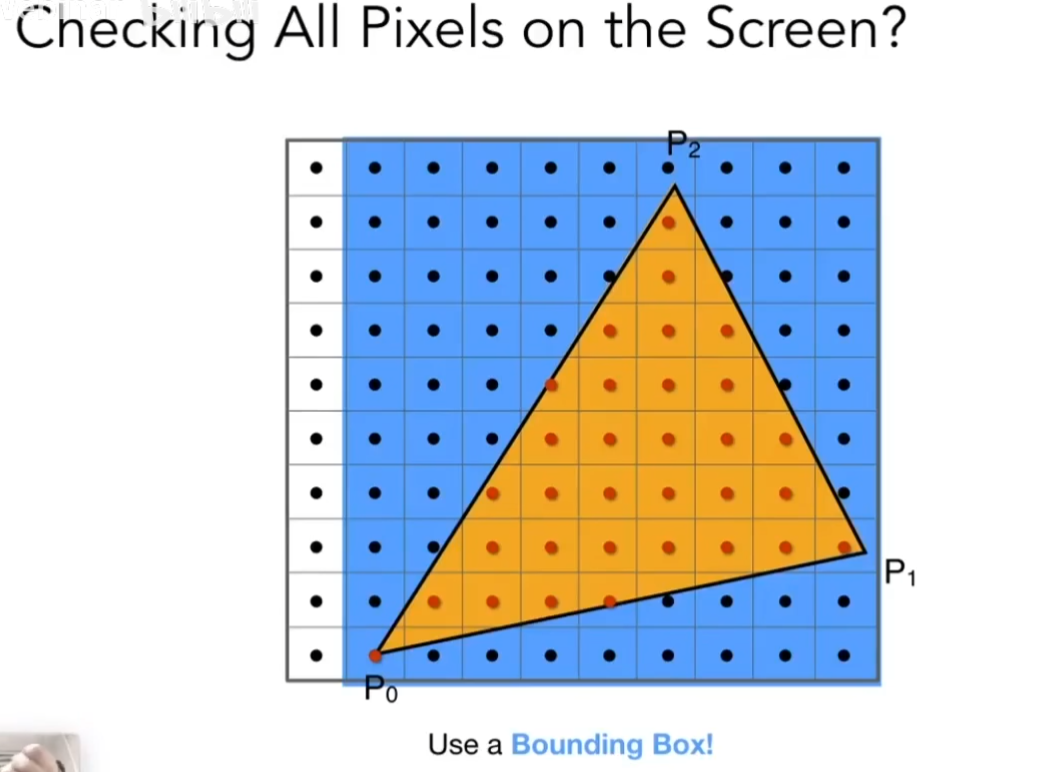
image-20220627201958345

更快的方法？可以对每一行进行扫描，出了范围就不再考虑到下一行，具体如下图：

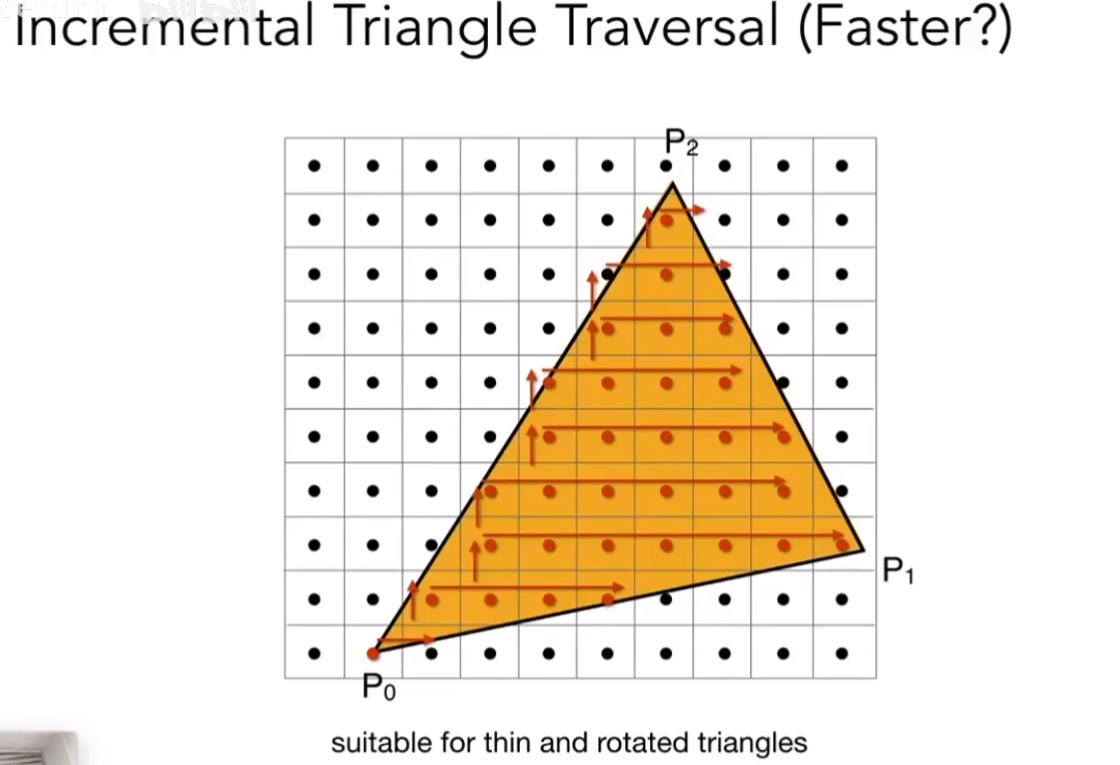
image-20220627202032627

Rasterzation(Antialiasing and Z-Buffer)，反走样和深度缓冲

走样

采样的方法会产生Artifacts(瑕疵/不真实)，如锯齿和摩尔纹

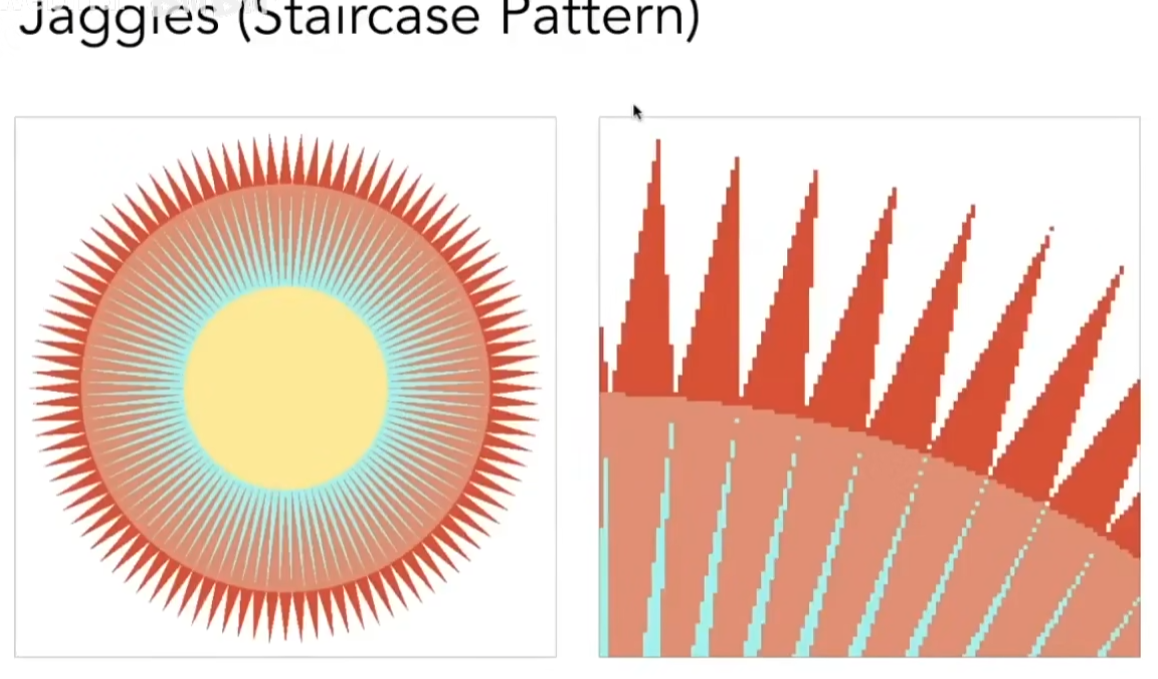
image-20220627203211900

image-20220627203250868

反走样的技术：

  • 模糊后再采样：

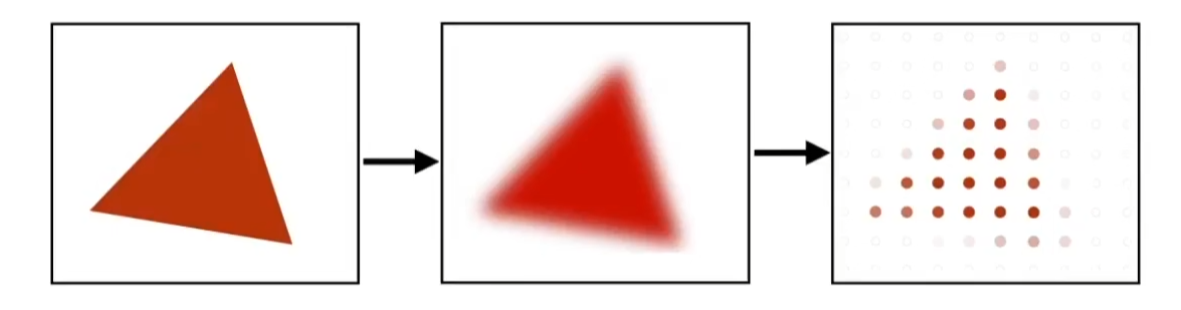
image-20220627203603753

先采样再模糊效果远不如先模糊再采样：

左图：先采样在模糊 右图：先模糊再采样

image-20220627203655313

傅里叶变换可以帮助我们描述一个复杂的函数：

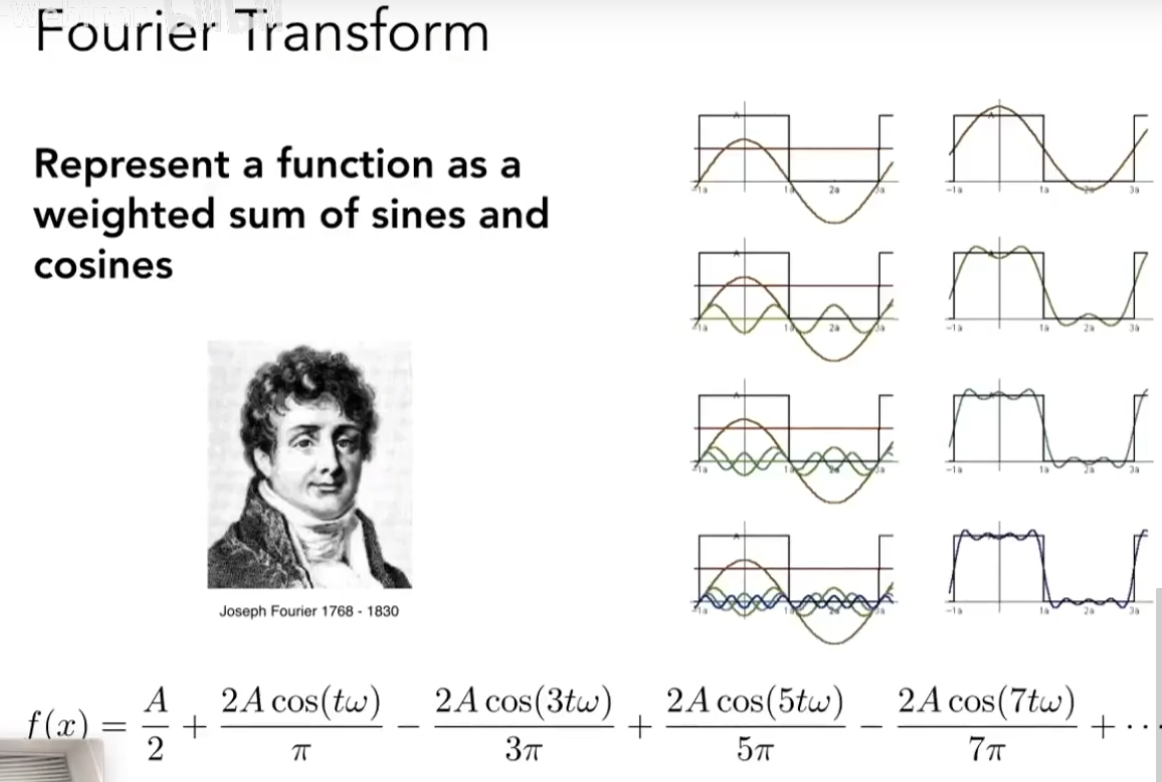
image-20220627204724323

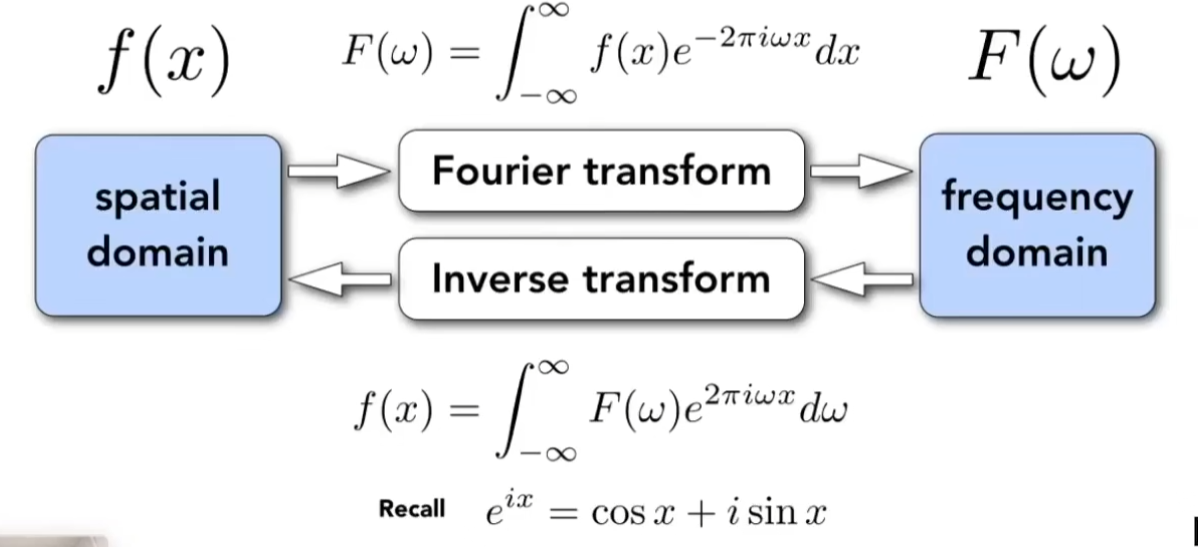
image-20220627204800289

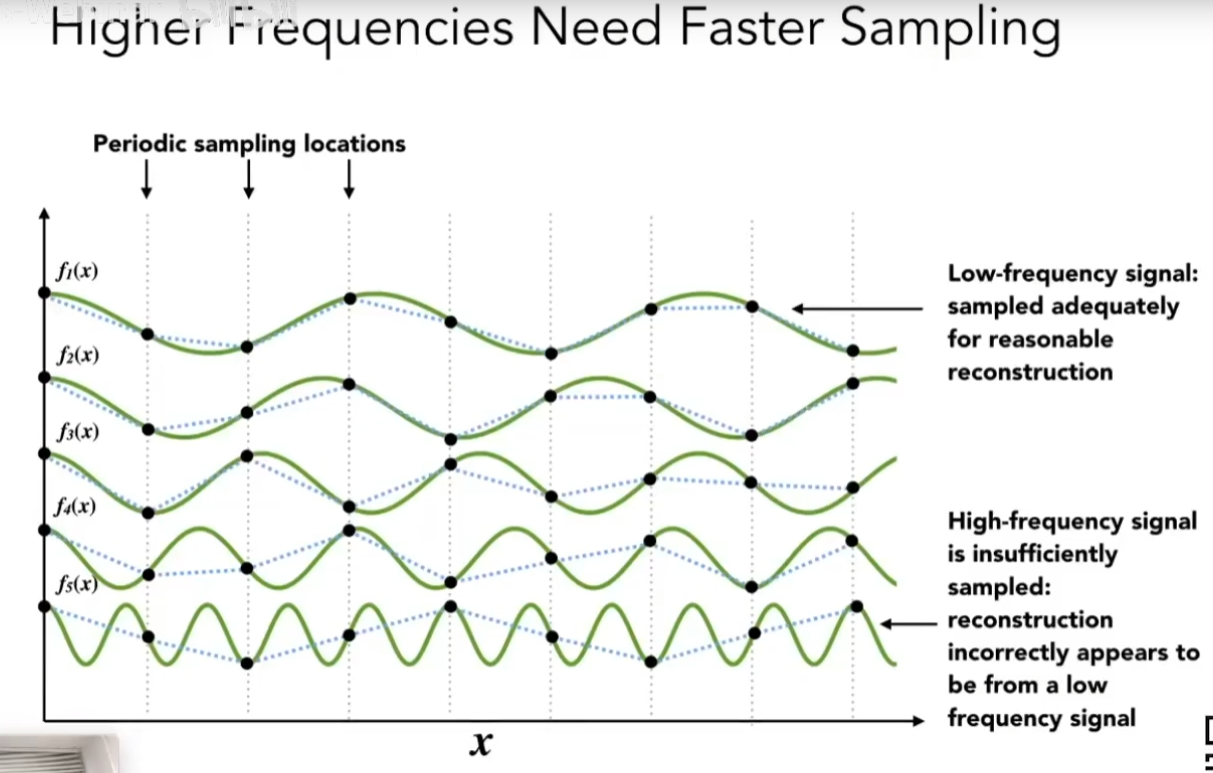
通过对下面不同频率的函数采样可以发现：

  • 采样频率高可以更好的反应函数的情况
  • 函数频率高采样不容易反应出函数的情况
  • 因此我们需要让 采样的频率 跟的上 函数的频率
  • 走样本质就是 采样无法分开两种频率的函数

image-20220627204950010

滤波

我们对一张图片做傅里叶变换，亮的地方表示低频信号，暗的地方表示高频信号。

image-20220630120118953

高通滤波：把低频信号抹去，留下高频。

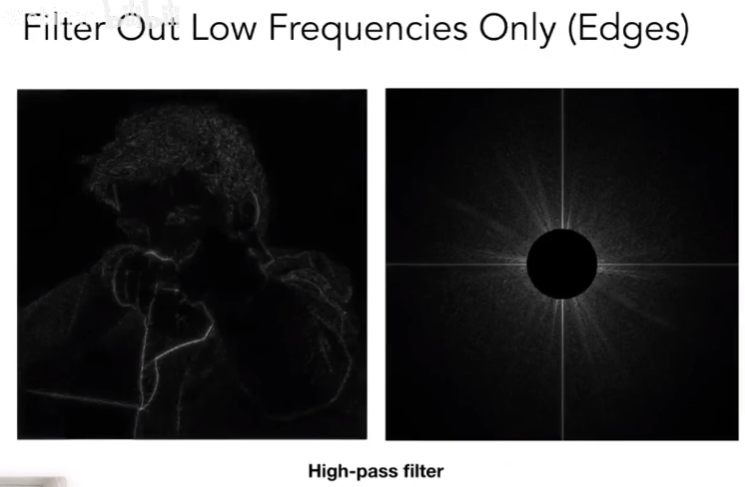
image-20220630120230975

低通滤波：把高频信息抹去

image-20220630120427981

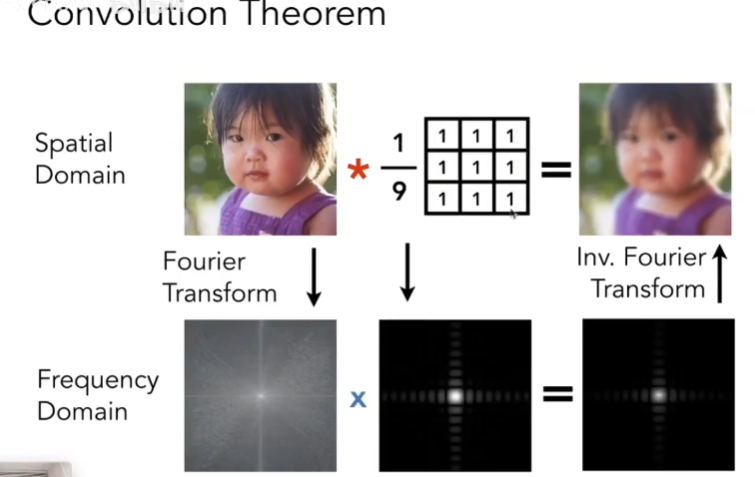
下面利用卷积实现了模糊的操作，可以发现滤波器的频域主要是保留低频信息： 在频域上表现为 图像的频域和卷积的频域相乘。

时域的卷积等于频域的乘积，反之亦然，时域的乘积等于频域的卷积

image-20220630120747997

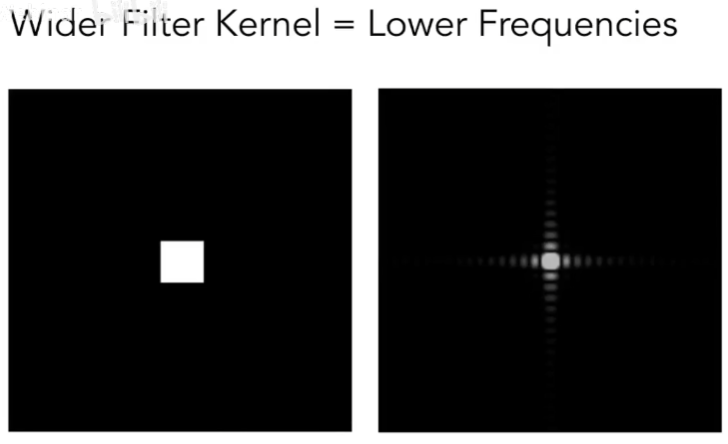
平均滤波器的size越大，其实会越模糊，表现在频域上为低频滤波减少(白点变小)

image-20220630122012669

image-20220630121953019

采样

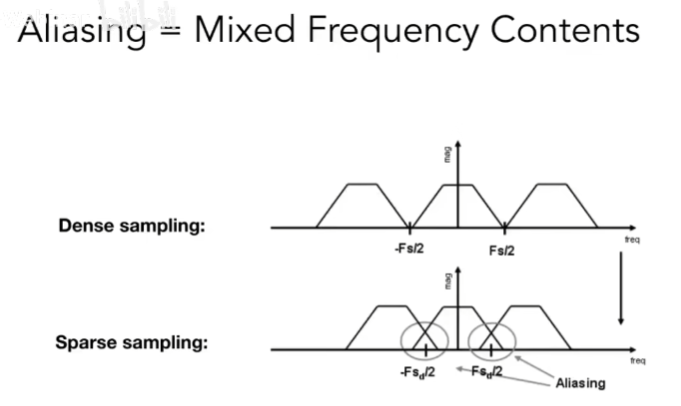
采样就是重复频域上的内容

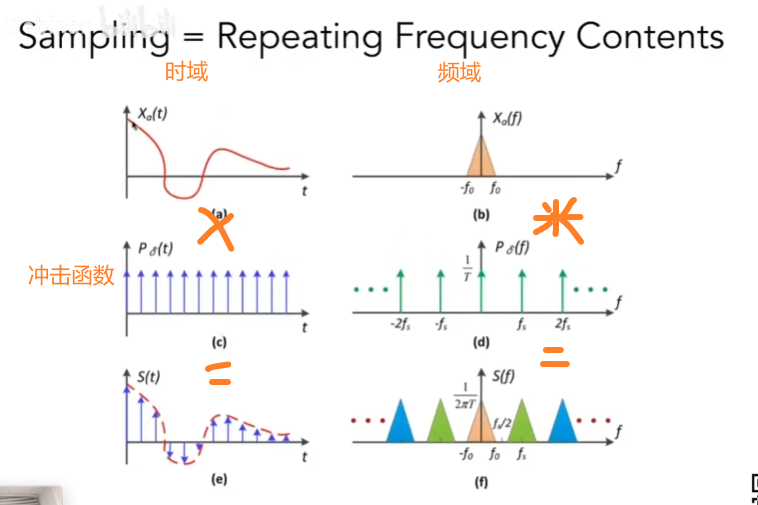
image-20220630134110852

冲激函数相当于采样，冲激函数(c)和(a)相乘得到(e), 可以发现相当于对a进行了采样，反映在频域上，时域上的乘积等于频域上的卷积，得到(f)，那么采样在频域上就是重复频谱。

在下图，采样频率过低会导致采样的频域间距大，频谱间隔小，导致频谱的混合，导致了走样

image-20220630134612296

反走样

image-20220630134903533

首先可以提高采样频率：即分辨率更高的显示器，像素点高，采样频率高。但是这种物理方法不是我们关注的方向。

还记得我们前面说的反走样方法吗？先模糊，再采样。

模糊可以把高频信息拿走，频谱覆盖的面小一些。

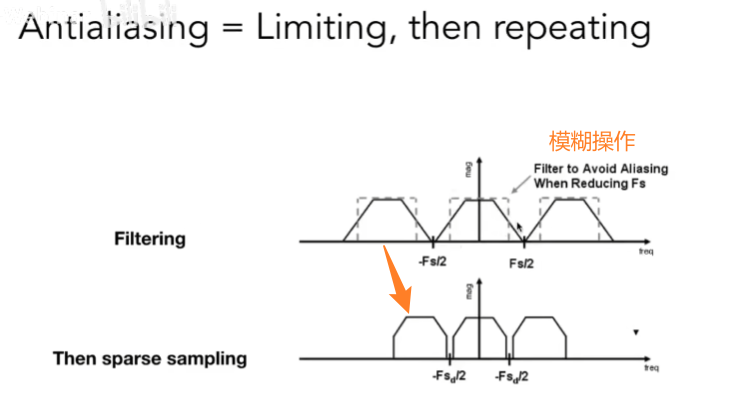
image-20220630135224063

我们用低通滤波器对三角形做卷积即可：

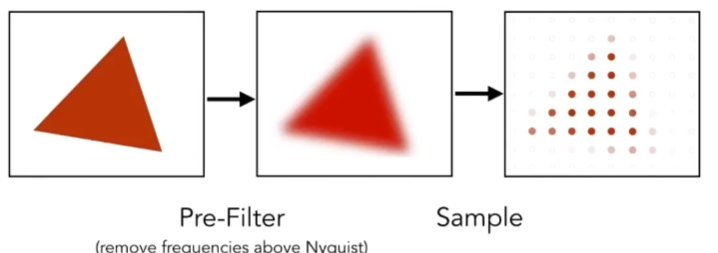
image-20220630135358262

image-20220630135439549

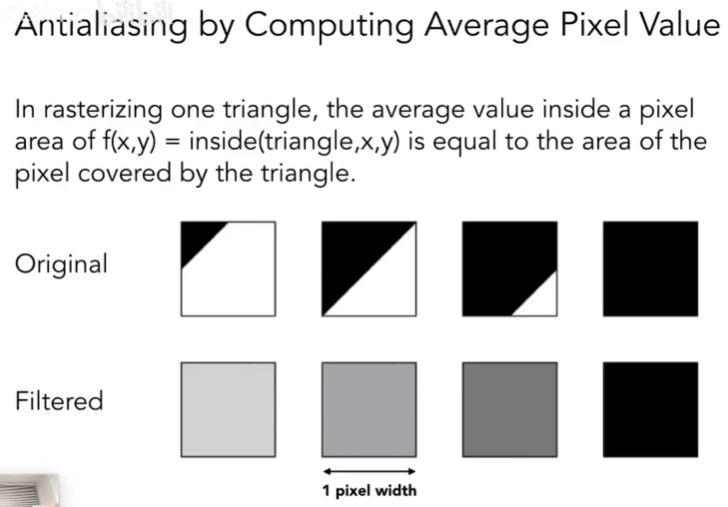
我们希望计算一个像素里三角形部分占多少，然后算一个颜色。但实际上这件事很难。这会消耗大量时间

image-20220630135651582

SSAA(SuperSampling AntiAliasing)超采样反走样

SSAA首先是模糊，然后把一个像素分成多份(比如$2*2$四份)，会对每一个pixel的subpixel都进行shading(着色计算)。 最后这个pixel的颜色等于四个subpixel的颜色的加权和。

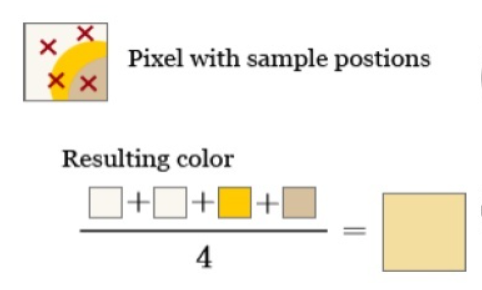
image-20220630173620785

MSAA(MultiSampling Anti-Aliasing)多重采样反走样

SSAA缺点很明显就是太慢，每个pixel需要计算4次(假设$2*2$情况时)shading。

MSAA最大的特点就是per pixel shading而不是per subpixel shading，这样对gpu的压力就减少很多。

下面介绍MSAA详细操作，体会下他的优势：

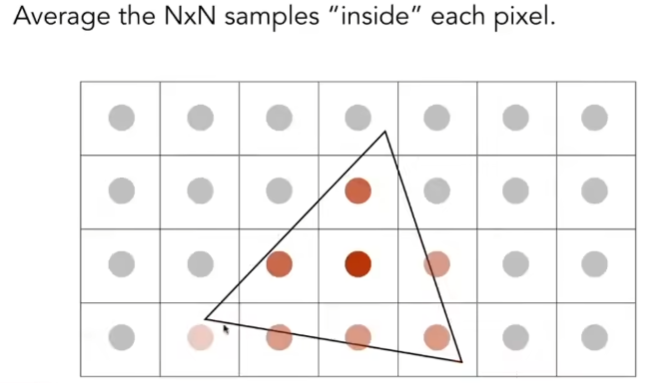
同样第一步需要先模糊, 然后我们把一个像素分成多份：

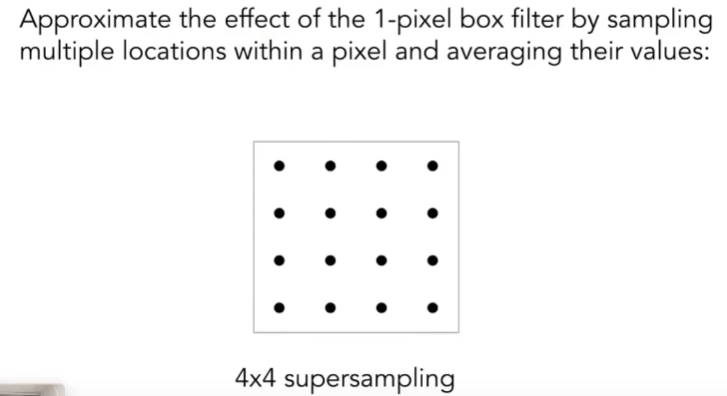
image-20220630140419631

原三角形

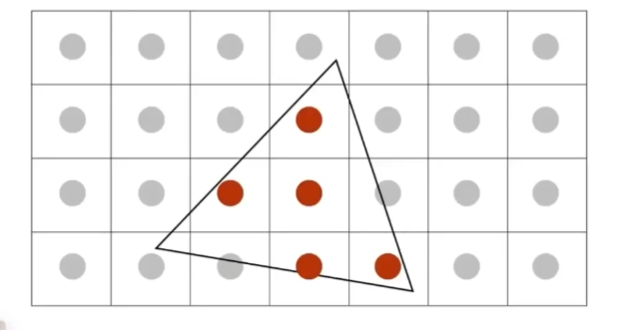
image-20220630140441479

$2*2$超采样

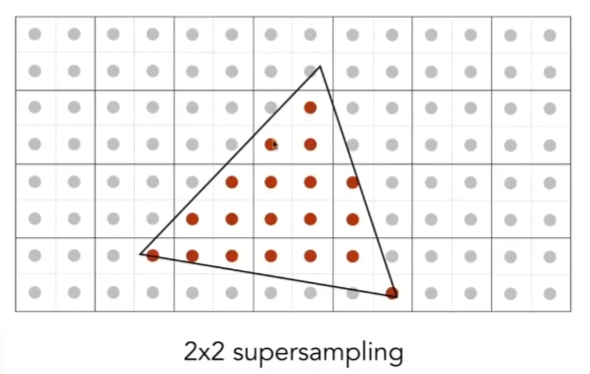
image-20220630140503622

计算加权颜色时：

这里SSAA则会在pixel shader着色阶段对pixel的每个subpixel进行计算，以上面图为例子就是需要计算4次。

而MSAA则只对pixel计算颜色，然后算subpixel有多少在三角形里(设为x)，$(包含的个数x/4)*pixel颜色$，然后一次pixel shading即可。

作者：文刀秋二
链接：https://www.zhihu.com/question/20236638/answer/44821615

拿4xSSAA举例子，假设最终屏幕输出的分辨率是800x600, 4xSSAA就会先渲染到一个分辨率1600x1200的buffer上，然后再直接把这个放大4倍的buffer下采样致800x600。这种做法在数学上是最完美的抗锯齿。但是劣势也很明显，光栅化和着色的计算负荷都比原来多了4倍，render target的大小也涨了4倍。

MSAA（Multi-Sampling AA）则很聪明的只是在光栅化阶段，判断一个三角形是否被像素覆盖的时候会计算多个覆盖样本（Coverage sample），但是在pixel shader着色阶段计算像素颜色的时候每个像素还是只计算一次。

image-20220630140534332

更多的 反走样/超采样 方法：

image-20220630141703852